電磁気学の種々の単位系
ジャクソンの電磁気学第2版上巻の付録によると、電磁気学の種々の単位系で変化する比例定数は2個だけである。クーロンの法則の比例定数(これで電荷量を定義する)と磁場の定義式である。
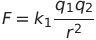
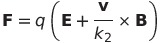
この中のk_1とk_2が種々の単位系で変わる。尚、定常閉電流間の要素間の力の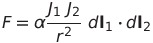 の中の比例定数
の中の比例定数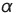 は
は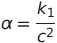 の関係がある。
の関係がある。
種々の電磁気学の単位系の比例定数表
下の表を見ると有理MKSA単位系がいかに特殊かがわかる。私はCGS静電単位系が一番自然だと思う。CGSガウス単位系は静電単位系と電磁単位系を合わせたもので、電荷は静電単位系と等しく、磁場は電流を光速で割ることによって電磁単位系と等しくしている。尚、SI単位系とは国際単位系のことで電磁気の分野では有理MKSA単位系のことである。
| 有理MKSA単位系(SI単位系) | cgsガウス単位系 | cgs静電単位系 | cgs電磁単位系 | cgsヘビサイド-ローレンツ単位系 | |
|---|---|---|---|---|---|
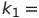 |
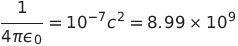 |
1 | 1 | 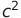 |
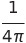 |
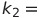 |
1 | 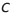 |
1 | 1 | 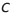 |
cgsガウス単位系と有理MKSA単位系(SI単位系)
ざっくばらんに言えば、cgsガウス単位系とは電流の測定時の時間を秒ではなく、光が1cm進んだときにかかる時間を単位として計ったものである。つまり光が1cm進んだあいだに電荷がどれだけ流れたかということである。形式的には秒を使っているので電流iが出てきたときはi/cと必ずcで割る。ついでに言えば、電荷の単位はクーロンの法則の比例定数が1になるように決めている。cgsと言うのはcm、g(グラム)、second(秒)の略である
方程式
| 一般 | SI単位系 | ガウス単位系 | |
|---|---|---|---|
| 比例定数1 | 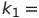 |
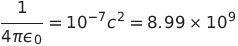 |
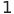 |
| 比例定数2 | 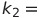 |
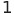 |
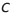 |
| クーロンの法則 | 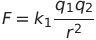 |
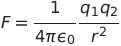 |
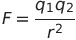 |
| 電場の定義 | 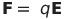 |
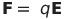 |
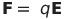 |
| 磁場の定義 | 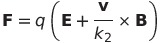 |
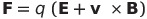 |
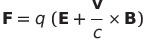 |
| ビオサバールの法則 | 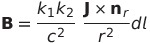 |
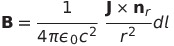 |
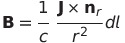 |
| マクスウェル方程式 | 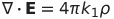 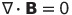 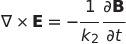 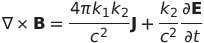
|
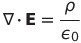 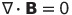 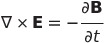 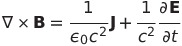
|
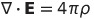 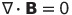 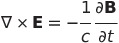 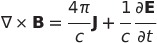
|
| ポテンシャル1 | 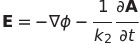 |
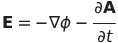 |
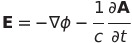 |
| 2 | 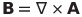 |
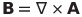 |
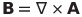 |
| 3(ローレンツ条件) | 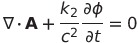 |
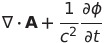 |
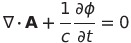 |
| 4 | 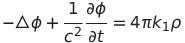 |
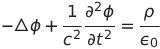 |
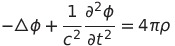 |
| 5 | 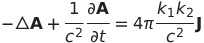 |
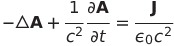 |
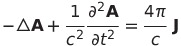 |
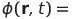 |
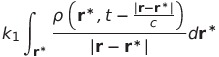 |
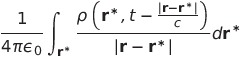 |
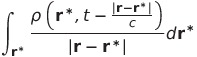 |
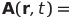 |
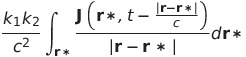 |
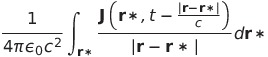 |
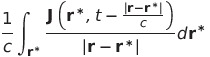 |
| エネルギーの流れ面密度 | 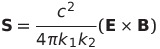 |
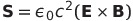 |
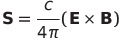 |
| エネルギー密度 | 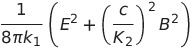 |
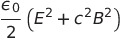 |
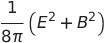 |
| マクスウェルの応力テンソル | 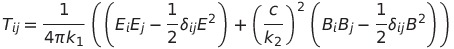 |
運動量流れ面密度の逆符号 | |
| 運動量密度 | 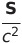 |
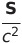 |
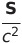 |
数値
表中の3.00は光の速度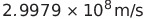 から来ている。だからより正確には2.9979に置き換えるとよい。
から来ている。だからより正確には2.9979に置き換えるとよい。
| MKSA有理単位系 | CGSガウス単位系 | |
|---|---|---|
| 電荷 | 1クーロン(C) | 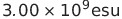 |
| 電流 | 1アンペア(A) | 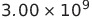 esu/s esu/s |
| 電圧 | 1ボルト(V) | 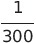 静電ボルト 静電ボルト |
| 電場 | 1(V/m) | 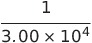 静電ボルト/cm 静電ボルト/cm |
| 磁場 | 1テスラ(T) | 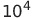 ガウス ガウス |
DやHについて
DやHを使う必要はないしかえって混乱すると思うのだが、だいたいの本に出ているので関係をまとめておく。Dの一般形は有理単位系(SIとヘビサイドローレンツ)では
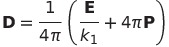
他の非有理単位系では
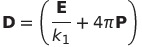
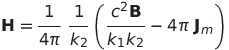
他の非有理単位系では
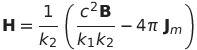
である。ここでJ_mは単位体積あたりの電流モーメントである。電流モーメントとは私の造語で閉電流の面積と電流をかけたもので、普通は磁気モーメントのことであるが、ガウス単位系とヘビサイド・ローレンツ単位系ではこれをcで割ると磁気モーメントになる。
| SI単位系 | ガウス単位系 | 備考 | |
|---|---|---|---|
| 電束密度Dの定義 | 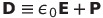 |
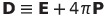 |
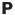 (分極密度)は単位体積あたりの双極子モーメント (分極密度)は単位体積あたりの双極子モーメント |
| 磁場Hの定義 | 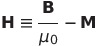 |
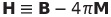 |
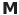 は磁気分極又は磁化といい単位体積当たりの磁気モーメント は磁気分極又は磁化といい単位体積当たりの磁気モーメント |
| 磁気モーメントの定義 | 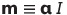 |
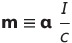 |
ガウス単位系では電流は必ずcで割る |
| 磁気双極子モーメントの定義 | 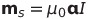 |
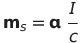 |
SI単位系では磁気モーメントと磁気双極子モーメントが異なることに注意 |
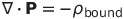 |
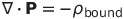 |
これについては少し異論がある | |
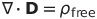 |
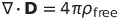 |
||
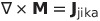 |
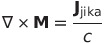 |
||
 |
 |
cで割ってないのは、電流で何かを定義しているわけではないから | |
| 磁荷密度の定義 | 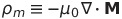 |
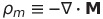 |
|
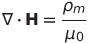 |
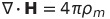 |
||
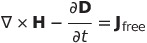 |
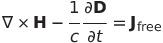 |
||
| 静止電気双極子モーメントにかかる力 | 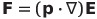 |
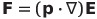 |
|
| 静止電気双極子モーメントにかかるトルク | 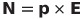 |
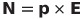 |
|
| 磁気モーメントにかかる力 |  |
 |
|
| 磁気モーメントにかかるトルク |  |
 |
|
| 静止電気双極子が遠方につくるポテンシャル | 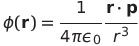 |
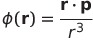 |
|
| 静止電気双極子が遠方につくる電場 | 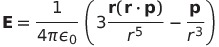 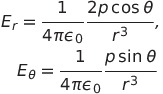 |
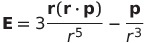 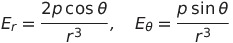 |
|
| 磁気モーメントが遠方につくるポテンシャル | 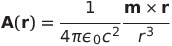 |
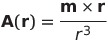 |
|
| 磁気モーメントが遠方につくる磁場 | 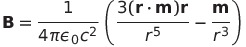 |
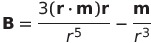 |
変換表
SI単位系からガウス単位系に移るには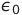 を1/4πにし、BをB/cに変えればよい。ガウス単位系からsi単位系に移るのはややこしい。比例定数のk_1が消えているからだ。基本的には電荷や電流が出てきたら
を1/4πにし、BをB/cに変えればよい。ガウス単位系からsi単位系に移るのはややこしい。比例定数のk_1が消えているからだ。基本的には電荷や電流が出てきたら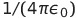 を掛けてやって、BはcBに置き換えればよい。正確には下記の表のように変換すればよい。
表中の添え字siはSI単位系。gaはガウス単位系。si単位系に矢印の式を代入するとガウス単位系の方程式になる。これはあくまで文字の変換であり数値の変換ではない。cgsガウス単位系ではcm、グラムを使っているからだ。もしMKSAガウス単位系なるものがあれば数値の変換になる。
を掛けてやって、BはcBに置き換えればよい。正確には下記の表のように変換すればよい。
表中の添え字siはSI単位系。gaはガウス単位系。si単位系に矢印の式を代入するとガウス単位系の方程式になる。これはあくまで文字の変換であり数値の変換ではない。cgsガウス単位系ではcm、グラムを使っているからだ。もしMKSAガウス単位系なるものがあれば数値の変換になる。
| 電荷密度 | 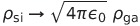
|
| 電場 | 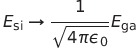
|
| 電流密度 | 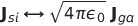
|
| 磁場 | 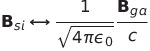
|
| スカラーポテンシャル | 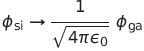
|
| ベクトルポテンシャル | 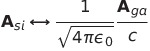
|