ガウス・クリューゲル投影法(横メルカトル投影)について
地球上から、測量で使わるている平面直角座標への変換であるガウス・クリューゲル投影法(横メルカトル投影)の解説です。2011年2月19日
第1章 序
なぜこの解説を書こうと思ったか、そのいきさつを述べよう。ガウス・クリューゲル投影法に基づく 平面直角座標は測量で使われている座標系である。ガウス・クリューゲル投影は横メルカトル投影ともいう。私が2004年頃、測量に興味を持って勉強を始めたころ、測量の教科書にこの投影法の解説があった。それによると、この投影法は地球回転楕円面上の点を平面上に、いわゆる等角写像するものだということだった。そして、その解説によると、この回転楕円面上から平面上への変換は図1のように、地球回転楕円
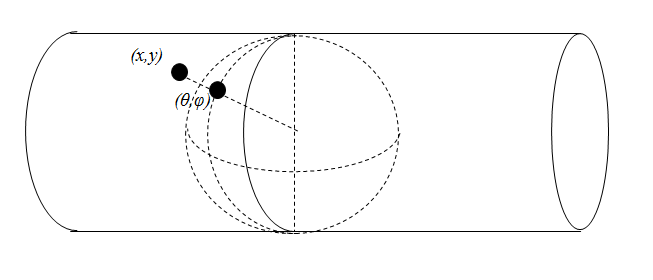
図1 誤ったガウス・クリューゲル投影の図
体に接するようにに楕円筒を入れて、地球の中心らしきところから筒上に直線を引き、直線と地球表面の交点を、直線と筒の交点に投影し、そしてこの筒を平面に広げたものという解説だった。詳しくは測量の教科書を見ていただきたい。私の知る限りすべての教科書はこのような 解説である。ところで少し考えればわかると思うが、この方法では決して等角写像にはならないのである。というのは、等角写像すなわち形を変えないためには 地球表面上のどの方向の微小変位も、それが写像される筒上の微小変位に対する拡大率 が等しくなければならない。ところがである、上図の写像では――簡単のために赤道上の点を写像を考える――明らかに東西の拡大率が南北方向の拡大率より大きくなってしまうのである。つまり等角写像にはならないのである。というわけで、私はガウス・クリューゲル図法とは何なのか本当のことを知りたくなった。そこでガウス・クルーゲル投影に関する本を探しに本屋さんに行ってみたが、本屋さんに行っても地図投影の本というのはないし、ガウス・クリューゲル投影を解説している本もなかった。そこで図書館に行き地図投影に関する文献を見つけてきて、ようやくこの投影法すなわちガウス・クリューゲル法のことを知ったのである。私が読んだのは「地図投影法 野村正七著 財団法人日本地図センター 昭和58年11月30日」である。ただこの本は地図投影の包括的な教科書であり、ガウス・クリューゲル投影に的をしぼったものではない。 この本は、おそらく伝統にしたがったのであろうが、複素関数の等角性から等角写像を導いている。私のこの解説では複素数は使わなかった。その方がわかりやすいと思ったからである。
地球回転楕円面上の点は、ガウス・クリューゲル投影法によって平面座標に写され、この平面座標を国家座標として、国や県、市町村の測量で使われている。我々の土地の登記図面もこの平面座標で表示されている。 それにもかかわらず、これを解説した本がない(注 いったい測量の公式を作成している国土地理院の人たちは何で勉強しているのかと思う。)。それで私がこの解説を書いてみようと思ったわけである。 この論文の読み方だが 第2章はとばしても全く問題ない。第3章がこの論文の核心でありガウス・クリューゲル投影法の解説である。
第2章 回転楕円体面上の線素
回転楕円体面上の線素を緯度\(\theta\)、経度\(\varphi\)で表したい。ここで\(\theta\)は図2のように
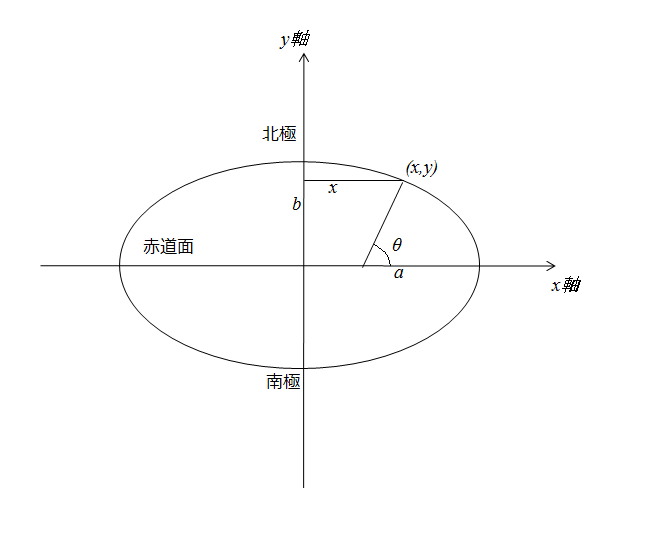
図2 地球回転楕円体断面図
楕円表面体上から垂線を延ばしその直線と赤道面とのなす角のことである。回転楕円体ではなく球の場合は線素はよく知られているように\((rd\theta,r\cos\theta d\varphi)\)である。一方
(回転楕円体の線素)
回転楕円体の線素は長半径を\(a\)、短半径\(b\)として \begin{equation} \left( \frac{a(1-e)^{2}}{(1-e^{2}\sin ^{2}\theta)^{3/2}}d\theta \ ,\ \frac{a\cos \theta}{(1-e^{2}\sin ^{2}\theta)^{1/2}}d\varphi \right) \end{equation} と表わされる。ここで\(e=\sqrt{(a^{2}-b^{2})/a^{2}}\)(離心率)である。
以下やや退屈だがこの式を導出する。もちろんこの章をとばしてもらっても後の理解にはいっさい関係ない。
2-1節 線素の導出
図2のように長半径\(a\)を\(x\)軸、短半径\(b\)を\(y\)軸に重ねて\((x,y)\)を\(\theta\)で表わせれば 線素は \begin{equation} \left( \sqrt{\left( \frac{dx}{d\theta} \right)^2+ \left( \frac{dy}{d\theta} \right)^2}\ d\theta\ ,\ x\ d\varphi \right) \label{sen} \end{equation} を計算すれば求まる。それでまず\(x,y\)を\(\theta\)で表わしてみよう。 楕円なので \begin{equation*} \frac{x^{2}}{a^{2}}+\frac{y^{2}}{b^{2}}=1 \end{equation*} である。ここで \begin{equation*} \frac{x}{a}=X\ \ ,\ \ \frac{y}{b}=Y \end{equation*} と置く。こう置いた方が計算が少し楽である。さて容易に \begin{equation*} \tan \theta=-\frac{dx}{dy} \end{equation*} であることがわかる(図3参照)。
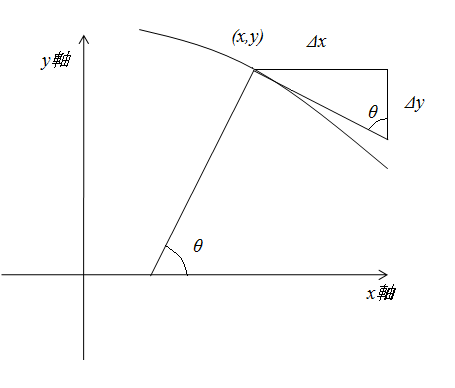
図3
\begin{equation*} -\frac{\Delta x}{\Delta y}=-\frac{a\Delta X}{b \Delta Y}\ \ \mbox{であり又}\ \ X^{2}+Y^{2}=1\ \ \mbox{ より}\ \ \frac{\Delta X}{\Delta Y}=-\frac{Y}{X}\ \ \end{equation*} よって \begin{equation*} \tan \theta=\left(\frac{a}{b}\right)\frac{Y}{X} \end{equation*} となる。これを自乗した \begin{equation*} \tan^{2} \theta=\left(\frac{a}{b}\right)^{2}\frac{Y^{2}}{X^{2}}\ \ \mbox{ と}\ \ X^{2}+Y^{2}=1 \end{equation*} を使うと \begin{equation*} X=\sqrt{\frac{(a/b)^{2}}{\tan^{2}\theta+(a/b)^{2}}}\ \ \ \ Y=\sqrt{\frac{\tan^{2}\theta}{\tan^{2}\theta+(a/b)^{2}}} \end{equation*} と求まる。\(x/a=X\ ,\ y/b=Y\)を使って変形すると \begin{equation*} x=\frac{a^2\cos\theta}{(a^{2}\cos^{2}\theta+b^{2}\sin^2 \theta)^{1/2}}\ \ \ \ y=\frac{b^2\sin\theta}{(a^{2}\cos^{2}\theta+b^{2}\sin^2 \theta)^{1/2}} \end{equation*} と求まる。さらに離心率\(e=\sqrt{(a^{2}-b^{2})/a^{2}}\)を使うと \begin{equation} x=\frac{a\cos\theta}{(1-e^{2}\sin^{2}\theta)^{1/2}}\ \ \ \ y=\frac{a(1-e^2)\sin\theta}{(1-e^{2}\sin^{2}\theta)^{1/2}} \label{x} \end{equation} と書ける。これで\(x,y\)が\(\theta\)を使って求まった。後は\(dx/d\theta\)と\(dy/d\theta\)を求めればよい。少し計算は面倒だが実行すると \begin{equation} \sqrt{\left( \frac{dx}{d\theta} \right)^2+ \left( \frac{dy}{d\theta} \right)^2}=\frac{a(1-e^{2})}{(1-e^{2}\sin^{2}\theta)^{3/2}} \label{bi} \end{equation} となる。以上式(\ref{sen}),(\ref{x}),(\ref{bi})より回転楕円体面上の線素 \begin{equation} \left( \frac{a(1-e^2)}{(1-e^{2}\sin ^{2}\theta)^{3/2}}d\theta \ ,\ \frac{a\cos \theta}{(1-e^{2}\sin ^{2}\theta)^{1/2}}d\varphi \right) \end{equation} が求まる。
第3章 ガウス・クリューゲル投影法
これ以降の章では測量で実際使われているのに合わせて縦軸を\(x\)、横軸を\(y\)とする。測量では北方向を\(x\)、東方向を\(y\)としているからである。あまり本質的なことではないが注意していただきたい。 前章で示したように緯度\(\theta\)、経度\(\varphi\)を使って線素は
(回転楕円体の線素)
\begin{equation} \left( \frac{a(1-e)^{2}}{(1-e^{2}\sin ^{2}\theta)^{3/2}}d\theta \ ,\ \frac{a\cos \theta}{(1-e^{2}\sin ^{2}\theta)^{1/2}}d\varphi \right) \end{equation}
となる。ここで\(e=\sqrt{(a^{2}-b^{2})/a^{2}}\)(離心率)である。さて、この線素を略して \begin{equation} \left(f(\theta)d\theta,g(\theta)d\varphi\right) \label{nagasa} \end{equation} と書く。つまり \begin{equation} f(\theta)=\frac{a(1-e)^{2}}{(1-e^{2}\sin ^{2}\theta)^{3/2}}\ \ ,\ \ g(\theta)= \frac{a\cos \theta}{(1-e^{2}\sin ^{2}\theta)^{1/2}} \end{equation} と略記する。
3-1節 等角写像の条件
線素が式(\ref{nagasa})で与えられたときに、楕円面上の点\((\theta,\varphi)\)から平面上(注 平面上のとは、普通の現実の平面のことである。平面上の点\((x,y)\)とは、現実の平面上に普通の直交した座標軸による座標点のことである。現実の平面とかをあまり考えない現代数学ふうに形式的に言えば平面上の点\((x,y)\)とは距離が\(\Delta x^2+\Delta y^2\)で与えられ角度はその点から半径\(1\)の円の弧の長さで与えられる座標系といってもいい。)の点\((x,y)\)への写像が等角写像となるための必要十分条件は\(x(\theta,\varphi),y(\theta,\varphi)\)が偏微分方程式 \begin{equation} \frac{1}{f(\theta)}\frac{\partial x}{\partial\theta}=\frac{1}{g(\theta)}\frac{\partial y}{\partial\varphi} \ \ ,\ \ \frac{1}{g(\theta)}\frac{\partial x}{\partial\varphi}=-\frac{1}{f(\theta)}\frac{\partial y}{\partial\theta} \label{hituyou} \end{equation} を満たすことである。これが等角写像になるための必要十分条件である理由を説明しよう。楕円体面上での緯度線上での微小変位\(g(\theta)\Delta\varphi\)は\((x,y)\)平面上で例えば角度\(A\)だけ回転し\(S\)倍されたとしよう(図4参照)。すると当然等角写像なのだから経線上の微小変位\(f(\theta)\Delta\theta\)は\((x,y)\)面上では角度\(A\)だけ回転し\(S\)倍されなければならない。これを行列で表わすと微小変位の変換は
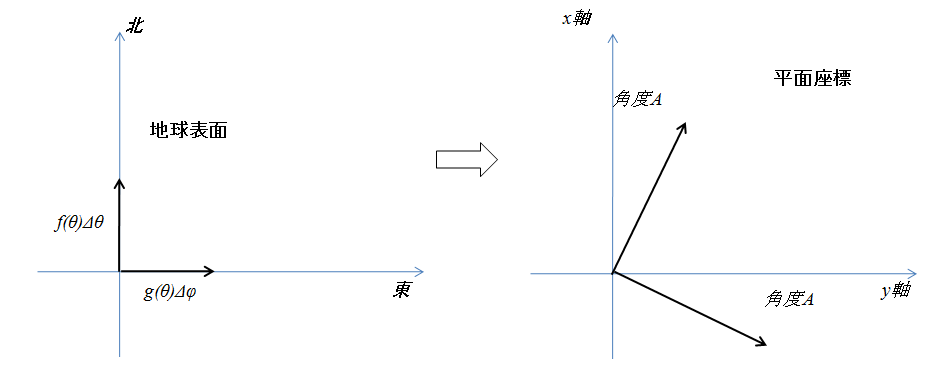
図4
\begin{equation} \left( \begin{array}{r} \Delta x \\ \Delta y \end{array} \right) =S \left( \begin{array}{rr} \cos A & -\sin A \\ \sin A & \cos A \end{array} \right) \left( \begin{array}{c} f(\theta)\Delta\theta \\ g(\theta)\Delta\varphi \end{array} \right) \label{kaiten} \end{equation} でなければならない。逆にこの式を満たしていれば、回転楕円体面上のすべての方向に対する変位は角度\(A\)だけ回転し\(S\)倍されるのは明らかであろう。よって式(\ref{kaiten})が成り立つことが等角写像のための必要十分条件である。角度\(A\)と拡大率\(S\)は任意なので式(\ref{kaiten})は結局式(\ref{hituyou})と同じことである。
3-2節 ガウス・クリューゲル投影
ガウス・クリューゲル投影は地球回転楕円体面上から平面への等角写像であり、基準となる経線が\(x\)軸に一致する変換である。その正確な定義を述べると
(ガウス・クリューゲル投影法)
ガウス・クリューゲル投影とは回転楕円体面上の緯度\(\theta\)、経度\(\varphi\)の点から、平面上の点\((x,y)\)への写像で、それを\(x(\theta,\varphi),\ y(\theta,\varphi)\)と書くと、偏微分方程式 \begin{equation} \frac{1}{f(\theta)}\frac{\partial x}{\partial\theta}=\frac{1}{g(\theta)}\frac{\partial y}{\partial\varphi} \ \ ,\ \ \frac{1}{g(\theta)}\frac{\partial x}{\partial\varphi}=-\frac{1}{f(\theta)}\frac{\partial y}{\partial\theta} \label{h} \end{equation} を満たし、かつ緯度\(\varphi=0\)で 基準となる経線上に\(x\)軸を一致させるという境界条件すなわち \begin{equation} x(\theta,0)=\int^\theta_0 f(t)dt\ \ ,\ \ y(\theta,0)=0 \label{kyoukai} \end{equation} を満たす写像のことである。ここで \begin{equation} f(\theta)=\frac{a(1-e)^{2}}{(1-e^{2}\sin ^{2}\theta)^{3/2}}\ \ ,\ \ g(\theta)= \frac{a\cos \theta}{(1-e^{2}\sin ^{2}\theta)^{1/2}} \end{equation}
である。これでこの変換(注 現在国土地理院で採用されている方法では全体を\(0.9999\)倍した写像すなわち境界条件を \begin{equation*} x(\theta,0)=0.9999\int^\theta_0 f(t)dt\ \ ,\ \ y(\theta,0)=0 \end{equation*} としている。さらに細かいことを言えば\(x\)座標の原点は赤道上ではなく適宜日本付近の位置に設定してある。上式で言えば積分定数の下が\(0\)を使わず、その緯度を使っている。)の本質的な説明は終わりである。あとは単なる数値計算の問題であり、例えば三角関数\(\sin x\)の値を与えられた\(x\)に対して求めるのと、困難さの程度は違うが、同じことである(注 少し余談になるが微分方程式の解を求めるとはどういうことかを考えてみよう。これは私の考えでは 「\(F(x)\)がある微分方程式の解として求まった」とは与えられた任意の\(x\)に対し任意の精度で\(F(x)\)の値を求める方法を知っているということである。もっと数学的に言うと、与えられた任意の\(x\)に対しどんなに小さな数\(\epsilon\)が与えられても \begin{equation*} A < F(x) < A + \epsilon \end{equation*} を満たす\(A\)を見つける方法を知っているということである。決してよく見たことのある関数の組み合わせ、すなわち掛け算、割り算又はその関数の関数で書けるということではない。)。
第4章 実際的解法(無限級数法)
さて偏微分方程式(\ref{h})をこの境界条件(\ref{kyoukai})のもとで\((x,y)\)を求めよう。さっきも述べたようにこれは数値計算の問題である。ここでは以下のような方法をとる。 \(x\)と\(y\)を下のように\(\varphi\)のべき乗で書き下し、それが偏微分方程式(\ref{h})と境界条件(\ref{kyoukai})を満たすように決めるというやり方である。 \begin{equation} \begin{array}{l} x(\theta,\varphi)=a_0(\theta)+a_1(\theta)\varphi+a_2(\theta)\varphi^2+a_3(\theta)\varphi^3+\cdots\\ y(\theta,\varphi)=b_0(\theta)+b_1(\theta)\varphi+b_2(\theta)\varphi^2+b_3(\theta)\varphi^3+\cdots \end{array} \label{tenkai} \end{equation} \(a_k(\theta),b_k(\theta)\)は\(\theta\)のみの関数とする。 計算の便宜のため偏微分方程式(\ref{h})を \begin{equation} \frac{\partial x}{\partial \varphi}=-\frac{g(\theta)}{f(\theta)}\frac{\partial y}{\partial\theta}\ \ \ ,\ \ \frac{\partial y}{\partial \varphi}=\frac{g(\theta)}{f(\theta)}\frac{\partial x}{\partial\theta} \label{kaki} \end{equation} と書きかえる。これに式(\ref{tenkai})を代入し\(\varphi^k\)の係数が等しくなるように\(a_k(\theta),b_k(\theta)\)を決めていく。まず式(\ref{kaki})の最初の式の左辺に式(\ref{tenkai})の\(x\)を代入すると \begin{equation*} \frac{\partial x}{\partial\varphi}=a_1+2a_2\varphi+3a_3\varphi^2+4a_4\varphi^3+\cdots \end{equation*} となり右辺に\(y\)を代入すると \begin{equation*} -\frac{g(\theta)}{f(\theta)}\frac{\partial y}{\partial\theta}=-\frac{g(\theta)}{f(\theta)}(b'_0+b'_1\varphi+b'_2\varphi^2+b'_3\varphi^3+\cdots) \end{equation*} となる。 ここで\(b'_k=db_k/d\theta\)のことである。以後ダッシュ記号\('\)を\(d/d\theta\)の意味で使う。\(\varphi^k\)の係数を比較して \begin{equation} a_k=-\frac{1}{k}\frac{g}{f}b'_{k-1}\ \ \ (k=1,2,3,\cdots) \label{a} \end{equation} をえる。又、式(\ref{kaki})の2番目の式の左辺に式(\ref{tenkai})の\(y\)を代入すると \begin{equation*} \frac{\partial y}{\partial\varphi}=b_1+2b_2\varphi+3b_3\varphi^2+4b_4\varphi^3+\cdots \end{equation*} となり右辺に\(x\)を代入すると \begin{equation*} \frac{g(\theta)}{f(\theta)}\frac{\partial x}{\partial\theta}=\frac{g(\theta)}{f(\theta)}(a'_0+a'_1\varphi+a'_2\varphi^2+a'_3\varphi^3+\cdots) \end{equation*} となる。 そして前と同様に \begin{equation} b_k=\frac{1}{k}\frac{g}{f}a'_{k-1}\ \ \ (k=1,2,3,\cdots) \label{b} \end{equation} を得る。 境界条件(\ref{kyoukai})より \begin{equation*} x(\theta,0)=\int^\theta_0 f(t)dt\ \ ,\ \ y(\theta,0)=0 \end{equation*} であり式(\ref{tenkai})で\(\varphi=0\)とおくと \begin{equation*} x(\theta,0)=a_0(\theta)\ \ ,\ \ y(\theta,0)=b_0(\theta) \end{equation*} よって \begin{equation*} a_0(\theta)=\int^\theta_0 f(t)dt\ \ ,\ \ b_0(\theta)=0 \end{equation*} を得る。あとはこれを順次、式(\ref{a})式(\ref{b})を使って \begin{gather*} a_0\to b_1\to a_2 \to b_3 \to a_4 \cdots\\b_0\to a_1\to b_2 \to a_3 \to b_4\cdots \end{gather*} のように求めていけばよい。 表にまとめると \begin{equation*} \begin{array}{|c|c|c|c|c|c|} \hline &k=0&k=1&k=2&k=3&k=4\\ \hline a_k & \int^\theta_0 f(t)dt & 0 & -\frac{1}{2!}\frac{g}{f}g' & 0 & \frac{1}{4!}\frac{g}{f}\left(\frac{g}{f}\left(\frac{g}{f}g'\right)'\right)' \\ \hline b_k & 0 & g(\theta) & 0 & -\frac{1}{3!}\frac{g}{f}\left(\frac{g}{f}g'\right)' & 0 \\ \hline \end{array} \end{equation*} ここで \begin{equation*} f(\theta)=\frac{a(1-e)^{2}}{(1-e^{2}\sin ^{2}\theta)^{3/2}}\ \ ,\ \ g(\theta)= \frac{a\cos \theta}{(1-e^{2}\sin ^{2}\theta)^{1/2}} \end{equation*} であり、 \begin{equation*} \frac{g}{f}=\frac{\cos\theta(1-e^2\sin^2\theta)}{(1-e^2)} \end{equation*} である。 この級数の収束性についてはは留保しておく。 思うが\(\varphi\)のべき乗の級数に展開などせず直接数値計算でこの偏微分方程式を解いてもいいと思う。 つまり格子上の数値計算で解いてもいいと思う。
4-1節 縮尺係数
縮尺係数とは測量用語で要するにこの変換の拡大率のことである。拡大率\(S\)は \begin{equation} S=\sqrt{\frac{(\Delta x)^2+(\Delta y)^2}{(f\Delta \theta)^2+(g\Delta \varphi)^2}} \label{s} \end{equation} を計算すればよいのであるが、この変換は等角写像なのでどの方向に対しても拡大率は等しいので \(\Delta \theta=0\)とすると計算が楽である。すると上式は \begin{equation} S=\frac{1}{g}\sqrt{\left(\frac{\partial x}{\partial \varphi}\right)^2+\left(\frac{\partial y}{\partial \varphi}\right)^2} \end{equation} となる。