日の出日の入り時刻の計算の考え方
2013年2月18日
第1章 地平座標

図1
図1のように太陽の位置を方向角と高度で表わす。これを地平座標と言う。日の出、日の入時刻の求め方と言うのは、要するに太陽の高度と方向角を時間の関数として求め、そして高度が\(-50'\)(注 高度が0度でない理由は太陽の視半径を考慮したのと大気の屈折のためである。詳しくは付録Aを見て欲しい。)となる時刻を求めるということである。しかし、ここで紹介する計算法は太陽の時角を求め、その時角から時刻を補正して求める方法である。時刻(年、日、時、分、秒)というのは太陽の位置から元々決めているので、こちらの方がわかりやすく簡明だと思う (注 時刻と言うものは、ある基準となる瞬間から計った時間というものとは違う。長さならば駅から2kmと言えば、駅を基準にしてそこからkmと言う長さが2個と言う意味である。しかし時刻にはそういう基準がない。実際、地球の自転に合わせるために時々、うるう秒をいれているようである。 時刻は数と言うよりも名称に近いものと言うのが私の印象である。)。
第2章 赤道座標

図2
もうひとつの太陽に位置の表わしかたの赤道座標を説明する。まず、言葉から説明しよう。天頂とは観測点の鉛直真上のことである(図1参)。天の子午線とは天の北極、天頂、天の南極を通る天球上の円のことである。要するに、真上頭上を南北に通る円のことである(図1、図2参)。図2のように太陽の位置を赤緯、時角で表わすのが赤道座標である。太陽、北極、南極を通る円を考え、赤道から太陽までの角度のことを赤緯\(\beta\)という。天の子午線からその円までの時計回りの角度を時角\(\theta\)という。時角の代わりに春分点から(注 春分点とは黄道と赤道の恒星上の交点のこと。第4章参照。)反時計回りに測った角度を赤経\(\gamma\)という。時角の代わりに赤経を使うこともある。 天球上の太陽の位置ベクトル\(\mathbf{T}\)は \begin{equation} \mathbf{T}=\mathbf{a}_1\sin\beta + \cos\beta(\mathbf{a}_2\cos\theta-\mathbf{e}_2\sin\theta) \label{tt} \end{equation} と表わせる。ここで\(\mathbf{a}_1\),\(\mathbf{a}_2\),\(\mathbf{e}_2\)は図2にあるような向きを持つ地面に固定された、互いに直交する単位ベクトルである(図3参)。
天球に恒星が固定されている。天球は天の北極のまわりを23時間56分で1周する。太陽は天球(恒星)と共に動きつつ1年で恒星を1周する。これが太陽の動きである。
第3章 赤道座標と地平座標の関係
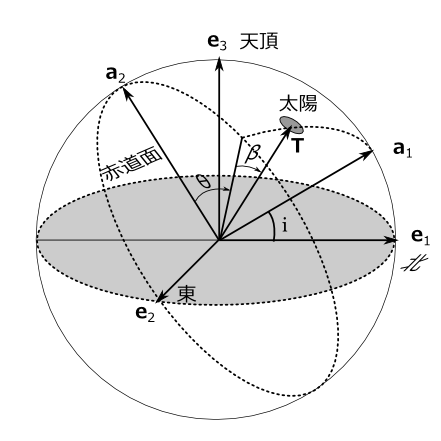
図3

図3
赤道座標と地平座標の関係を説明する。図3のように地平上の真北方向の単位ベクトルを\(\mathbf{e}_1\)、東方向を\(\mathbf{e}_2\)、天頂方向を\(\mathbf{e}_3\)とする。\(\mathbf{a}_1\),\(\mathbf{a}_2\)は前節で述べたものと同じである。\(i\)はその地点の緯度である。\(\mathbf{a}_1\)、\(\mathbf{a}_2\)を\(\mathbf{e}_1\)、\(\mathbf{e}_3\)で表わすと \begin{equation} \mathbf{a}_1=\mathbf{e}_1\cos i+\mathbf{e}_3 \sin i \quad \quad\quad\mathbf{a}_2=\mathbf{e}_3\cos i-\mathbf{e}_1 \sin i \end{equation} これを式(\ref{tt})の \[ \mathbf{T}=\mathbf{a}_1\sin\beta + \cos\beta(\mathbf{a}_2\cos\theta-\mathbf{e}_2\sin\theta) \] に代入すると \begin{equation} \mathbf{T}=\mathbf{e}_1(\cos i\sin\beta-\sin i\cos\beta\cos\theta)+\mathbf{e}_2(-\cos\beta\sin\theta)+\mathbf{e}_3(\sin i\sin\beta+\cos i\cos\beta\cos\theta) \end{equation} だから高度と方向角は \begin{equation} \sin(\text{高度})=\sin i\sin\beta+\cos i\cos\beta\cos\theta \label{koudo} \end{equation} \begin{equation} \tan(\text{方向角})=\frac{\cos\beta\sin\theta}{\sin i \cos\beta\cos\theta-\cos i\sin\beta} \label{houkou} \end{equation} と表わせる。これが赤道座標と地平座標の関係である。太陽の高度が\(-50'\)のとき日の出、日の入となるのであった。
【例題】緯度35度の地点で太陽の赤経\(\beta\)を10°として日の出、日の入時刻とその方向角の概算を求めてみよう。
式(\ref{koudo})より \begin{equation} \theta=\cos^{-1}\left(\frac{\sin (\text{高度})-\sin i\sin \beta}{\cos i\cos\beta}\right) \label{theta} \end{equation} この式に、高度\(=-50'\)、\(\beta=10\)、\(i=35\)を入れると、\(\theta=\pm 97.9327\)をえる。大ざっぱに言えば、太陽の時角は正午に0°で、24時間で360°進む。つまり1時間で15°、4分で1°進む。だから \begin{equation} \text{12時}\pm 97.9327 \times \text{4分} \end{equation} を計算して、日の出が5時28分、日の入りが18時32分となる。
方向角は式(\ref{houkou})に\(\theta=\pm 97.9327\)を入れると\(\pm77.3\)°を得る。式(\ref{houkou})の代わりに \[ \text{方向角}=\cos^{-1}\left( \frac{\cos i \sin \beta -\sin i\cos \beta \cos\theta}{\cos (-50')} \right) \] を使ってもよい。 【終】
この計算で正午に時角が0°というのは計算が大ざっぱすぎるのでその補正をしなければならない。それと基準となる経度からの補正も必要である。それは第8章で説明しよう。まず何月何日に赤経\(\beta\)の値がどれだけになるかを求めよう。
第4章 公転角と赤経、赤緯
太陽の通る天球(恒星)上の道を黄道という。黄道を通る面は赤道面に対して\(K=\)23.44°の傾きをもつ。 黄道面と赤道面の天球(恒星)上の交点をそれぞれ春分点、秋分点という。太陽は天の北極から見て反時計回りに回る。

図4
図4のようにたがいに直交する天球(恒星)上に固定された単位ベクトル\(\mathbf{b}_1,\mathbf{b}_2,\mathbf{b}_3,\mathbf{c}\)を取ろう。太陽の天球(恒星)上の回転角を公転角と呼び、春分点からの角度を\(\alpha\)としよう。太陽に位置ベクトルは \begin{equation} \mathbf{T}=\mathbf{b}_2\cos \alpha + \mathbf{c}\sin \alpha \end{equation} となる。一方、 \[ \mathbf{c}=\mathbf{b}_1\cos K+\mathbf{b}_3\sin K \] なので代入すると \[ \mathbf{T}=\mathbf{b}_1\cos K\sin\alpha+\mathbf{b}_2\cos\alpha+\mathbf{b}_3\sin K\sin\alpha \] となる。だから赤緯\(\beta\)は \begin{equation} \sin\beta=\sin K\sin\alpha \end{equation} 赤経\(\gamma\)は \begin{equation} \tan \gamma=\tan\alpha\cos K \end{equation} となる。
第5章 公転角と時刻、時間の関係
公転角の角速度は場所によって異なる。冬至の頃が一番速く、夏至の頃が遅い。例えば冬至、春分、夏至、秋分間の日数は、もし角速度が一定なら、同じはずだが実際は
2011年冬至→(89日)→2012年春分→(93日)→夏至→(93日)→秋分→(90日)→冬至
と日数が異なる。
5.1節 地球の軌道

図5
図5のように地球は太陽を焦点とした楕円上を回転している。回転しているというのは恒星系に対してである。現在は近日点と春分点との差は約77°らしい。公転は北極の側から見て反時計回りである。近日点は年に約\(11"\)、地球の公転方向に、恒星系に対して動く(注他の惑星の影響らしい)。春分点は年に約\(50.3"\)、地球の公転方向とは逆向きに、恒星系に対して動く(注 地軸が歳差運動で回転しているためである。)。つまり春分点は年に\(61.3"\)近日点に近づくわけである。
5.2節 1年について
1年の長さの定義には3つある。近点年と恒星年と太陽年である。 1近点年とは地球が近日点から近日点に行くまでの時間のことである。1恒星年とは地球が恒星系に対して1周する時間のことである。1太陽年とは地球が春分点から春分点に行くまでの時間のことである。 数値を上げると
1近点年=365.25963555日=365日6時間13分52.512秒
1恒星年=365.25636304日=365日6時間9分9.767秒
1太陽年=365.24219029日=365日5時間48分45.241秒
である(天文学概論 鈴木敬信著 地人書館 1983年)。恒星を固定して地球から見ると近日点と春分点の動きは図6のようになる。
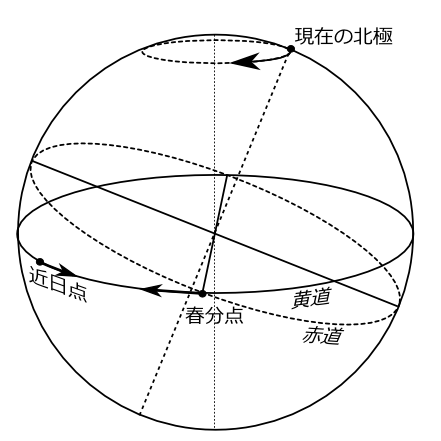
図6
5.3節 公転角の時間発展
楕円の方程式は \begin{equation} r=\frac{l}{1+e\cos\varphi} \end{equation} である。ここで\(e\)は楕円の離心率で地球の場合は0.01672である。\(\varphi\)は太陽から見た近日点から地球までの角度、\(l\)は定数、\(r\)は地球と太陽の距離である(図5)。ケプラーの面積速度一定の法則\(r^2\dot{\varphi}=\)一定より \begin{equation} \frac{d\varphi}{dt}=A(1+e\cos\varphi)^2 \end{equation} となる。ここで\(A\)は定数。\(A\)の値は、この式を \begin{equation} dt=\frac{d\varphi}{A(1+e\cos\varphi)^2} \label{bunri} \end{equation} と変数分離して両辺を積分して \[ \int_0^{360}\frac{d\varphi}{A(1+e\cos\varphi)^2}=\text{1近点年}\Longleftrightarrow A=\frac{\int_0^{360}\frac{d\varphi}{(1+e\cos\varphi)^2}}{\text{1近点年}} \] で求める。1近点年=365.25963555日、\(\int_0^{360}\frac{d\varphi}{(1+e\cos\varphi)^2}=360.1510143\)(注 積分値は関数電卓の積分機能で求めた。)なので \[ A=0.986013726 \] と求まる。
春分点は図5にあるとおり、現在は近日点から約77°だけ公転方向にあるので\(\alpha=\varphi-77\)とすればいいのだが、春分点と近日点は年に\(61.3"\)づつ近づくことを考慮して \begin{equation} \frac{d\alpha}{dt}=A_{T}(1+e\cos\varphi)^2\Longleftrightarrow \frac{d\alpha}{dt}=\frac{A_{T}}{A} \frac{d\varphi}{dt} \label{t} \end{equation} とする。ここで \begin{align} A_{T} & =\frac{\int_0^{360}\frac{d\varphi}{(1+e\cos\varphi)^2}}{\text{1太陽年}}=\frac{\text{1近点年}}{\text{1太陽年}}\cdot A=0.98606082 \end{align} である(注 \(\frac{d\alpha}{dt}\)を他の式を使ってもいいのだが、日の出、日の入の時刻計算では大した影響はでない。又、単に\(\alpha=\varphi-77\)としても10年や20年ではたいして誤差は生じないであろう。)。この式(\ref{t})を使うと公転角\(\alpha\)は1太陽年で360°回ってくれる(注 厳密には360°回らない。\(\varphi\)の角速度が場所によって異なるからである。)。
まとめると \begin{align} & \frac{d\varphi}{dt}=A(1+e\cos\varphi)^2\\ & \frac{d\alpha}{dt}=A_{T}(1+e\cos\varphi)^2\\ & A=0.986013726\quad A_{T}=0.98606082 \end{align} 初期条件として\(t=t_0\)のとき\(\alpha=\alpha_0,\varphi=\varphi_0\)として \[ \alpha_0=\varphi_0-77 \] の関係があるとする (注 77°というのはおよその値である。これが1度くらい異なっていても日の出日の入時刻の計算には影響ない。 ) 。
第6章 太陽の時角と時刻
先の例題では太陽の時角が0°なら12時、90°なら18時、つまり時角に時間が比例するものとして計算した。しかし正確には比例しない。時角が0°でも12時とは言えないのである。というのは太陽の時角が360°進むのに要する時間が図7のように季節によって異なるからである。
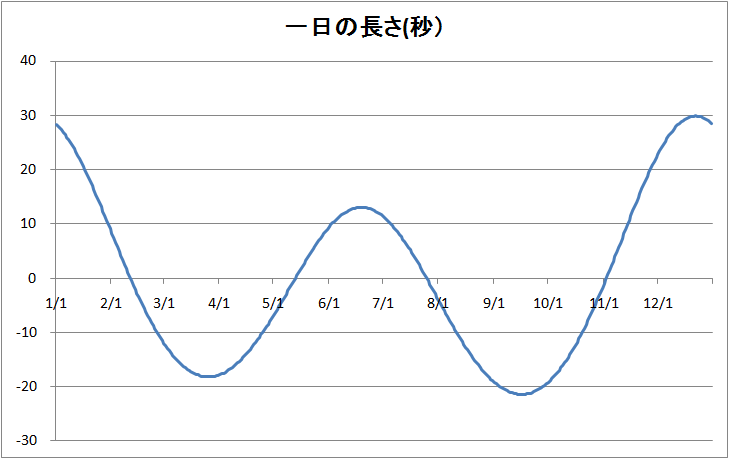
図7 太陽の時角が360°増えるのにかかる時間のグラフ。縦の目盛は秒。横軸は日付。縦が10なら24時間10秒かかるという意味。12月中旬が最も長く。24時間30秒程。最も短いのが9月中旬で23時間59分39秒程。
その原因は一つは太陽の角速度が季節によって異なるからであり、もう一つは黄道面が赤道面に対して傾いているからである。太陽が夏至や冬至のころに1°だけ\(\alpha\)が増加したときの赤経\(\gamma\)の増加量は、春分点や秋分点の頃のそれより大きくなる。これは例えば地球上では緯度の大きい地域では東にわずかに動いただけで経度が沢山増えることからも想像がつくであろう。
さて、これを定量的に式で表わそう。話をわかりやすくするために、仮想物体Hを考えよう。Hは一様な角速度で天の赤道を太陽と同じ方向に回り24時間で天の子午線を1周するとする。そして、【Hの時角×4分】を時刻とする。4分と言うのは24×60分÷360から来たものである。Hの初期条件はHの時角と太陽の時角の差の時間平均が0となるように決める。\(H_\theta\)をHの時角とすると\(H_\theta-\theta\)の時間平均を0としたいわけである。ここで\(\theta\)は太陽の時角である。
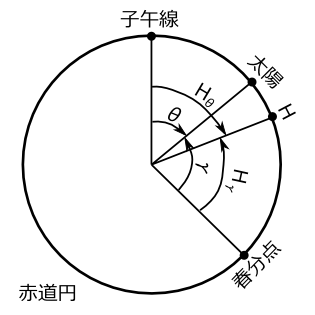
図8
図8から \[ H_\theta-\theta=-(H_\gamma-\gamma) \] の関係があることがわかる。ここで\(H_\gamma\)はHの赤経のことである。\(H_\gamma\)は一定の割合で増加し、1太陽年で360°増える (注 もともと24時間と言う時間の長さは、1太陽年で春分点を1周する物体が子午線を1周する長さと定義したからである。)。この\(H_\gamma-\gamma\)の時間平均が0になるように\(H_\gamma\)の初期条件を決めればいいわけである。 \[ H_\gamma-\gamma=(H_\gamma-\alpha)+(\alpha-\gamma) \] と変形しよう。第2項\(\alpha-\gamma\)の時間平均は図の対称性からほぼ0になる(図9参)(注 ただ太陽の滞在時間が公転角の値によって異なるので厳密には0にならないと思う)。
太陽が近日点にいるときに\(H_\gamma\)が太陽の公転角\(\alpha\)と等しければ第1項の時間平均は0になる(注 我々の計算モデルでも厳密には一致はしないと思うが。角速度が場所によって異なり、春分点と近日点が動くからである。)。なぜなら、公転角\(\alpha\)の角速度は近日点に関して対称だからである(図9参)。\(t_K\)を近日点の時刻、\(\alpha_K\)をそのときの公転角とすると、\(H_\gamma\)は、\(V=\frac{360}{\text{1太陽年}}=0.98564736\)として \begin{equation} H_\gamma=V\cdot(t-t_K)+\alpha_K \label{h} \end{equation} とすればよいということである。まとめると太陽の時角と時刻の関係は \begin{align} 12\text{時}+H_\theta \times 4\text{分} & =12\text{時}+\left( (H_\theta-\theta)+\theta\right)\times 4\text{分}\\ & =12\text{時}+\left( (\gamma-H_\gamma)+\theta\right)\times 4\text{分}\\ & =12\text{時}+\left((\alpha-H_\gamma)+(\gamma-\alpha)+\theta\right)\times 4\text{分} \end{align} と求めればよいことになる。
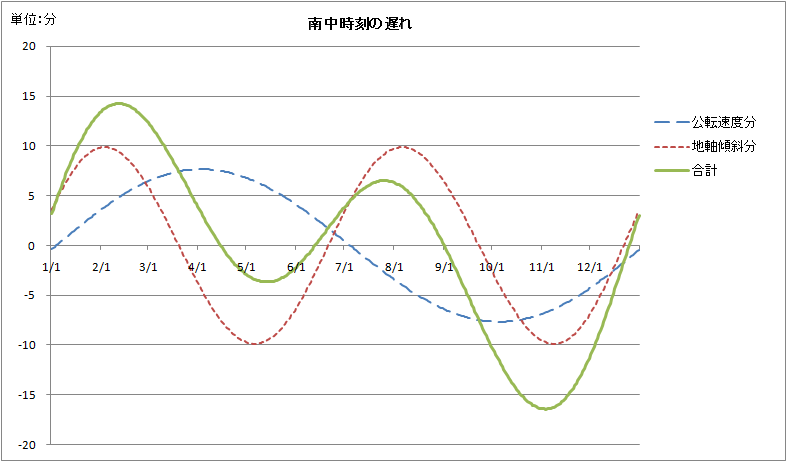
図9
図9は太陽の位置と時刻の差のグラフである。\((\alpha-H_\gamma)\times\)4分が公転角速度による分で、\((\gamma-\alpha)\times\)4分が地軸傾斜による分である (注 ここでは\(H_\gamma\)を式(\ref{h})のように求めたが、別の方法もそしてある意味簡単な方法もある。要は\(H_\gamma-\gamma\)の時間平均が0になるようにすればよいのだから、\(t_1\)を任意の時刻として \[ H_\gamma(t)=V\cdot (t-t_1)-\overline{(V\cdot (t-t_1)-\gamma)} \] とすればよいのである。ここで\(\overline{(V\cdot (t-t_1)-\gamma)}\)は1年間の時間平均、\(t_1\)はいつでもよいが例えば1月1日0時にでもしとけばいいであろう。この方法が本来なのだが、一度時間平均を計算しなければならないというのが面倒である(1年間すべての計算をするのならついでにすればいいのだが。)。一方本文のしかただと一度近日点の時刻を計算しなければならないという面倒さがある。 )。
第7章 近日点の時刻
ここで近日点の時刻を計算してみよう。すでに書いたように初期条件は
\(t_0=\)2011年12月22日14時31分\quad \(\alpha_0=\)270°\quad \(\varphi_0=\)347°
とする。近日点の時刻\(t_K\)は式(\ref{bunri})より \[ t_K=\int^{360}_{347}\frac{d\varphi}{A(1+e\cos \varphi)^2}+t_0=\text{2012年1月4日8時42分} \] となる。積分は関数電卓の積分機能で行った。また近日点における公転角\(\alpha_{K}\)は式(\ref{t})より \(\Delta \alpha=\frac{A_T}{A}\Delta \varphi\)なので \[ \alpha_{K}=\frac{A_T}{A}\cdot 13+270=283.0006 \] となる。
第8章 経度による補正
日本の時刻は経度135°の地点を基準にしている。経度が大きい方が日の出が早い。補正値は \begin{equation} (135-\text{その地点の経度})\times 4\text{分} \label{hosei} \end{equation} である。
第9章 計算方法のまとめ
\(e\)は離心率、\(K\)は地軸の黄道に対する傾き、\(i\)は観測点の緯度、値は \begin{align} e=0.01672\quad K=23.44 \end{align} 近日点からの太陽(地球)の回転角\(\varphi\)、春分点からの公転角\(\alpha\)は \begin{align} & \frac{d\varphi}{dt}=A(1+e\cos\varphi)^2\Longleftrightarrow \varphi=\int^t_{t_0}A(1+e\cos\varphi)^2dt+\varphi_0\\ & \frac{d\alpha}{dt}=A_{T}(1+e\cos\varphi)^2 \Longleftrightarrow \alpha=\frac{A_T}{A}(\varphi-\varphi_0)+\alpha_0\\ & A=0.986013726\qquad A_{T}=0.98606082\qquad t_0=\text{2011年12月22日14時31分}\\ & \varphi_0=347\qquad \alpha_0=270 \end{align}に従う。近日点の時刻\(t_K\)とその時の\(\varphi\)、\(\alpha\)は \begin{align} t_K=\text{2012年1月4日8時42分}\qquad \varphi_K=0\qquad \alpha_K=283.0006 \end{align} である \footnote{ この近日点の時刻(冬至もそうだが)は経度135°の日本の標準時である。他の経度\(X\)では \[ \frac{(X-135)}{15} \, \text{時間} \qquad -180\le X\le 180 \] を加えなければならない。 例えば経度\(-\)75°のニューヨークでは近日点の時刻は14時間引いて2012年1月3日20時42分となる。\(\alpha,\, \varphi\)の値は当然同じ \(\varphi_K=0,\quad \alpha_K=283.0006\)である。 } 。これを初期条件として使ってもよい。 太陽の赤緯\(\beta\)、赤経\(\gamma\)は \begin{equation} \beta=\sin^{-1}\left(\sin K\sin\alpha\right)\qquad \gamma=\tan^{-1}\left(\tan\alpha\cos K\right) \label{seki} \end{equation} である。日の出没しそうな時間を大ざっぱに決めて、例えば朝6時を日の出と仮定して、\(\alpha,\, \beta,\, \gamma\)が決め、それを使って太陽の出没時角 \begin{equation} \theta=\cos^{-1}\left(\frac{\sin (\text{高度})-\sin i\sin \beta}{\cos i\cos\beta}\right) \label{ji} \end{equation} を決める。太陽の出没方向角は \begin{equation} \text{方向角}=\tan^{-1}\left(\frac{\cos\beta\sin\theta}{\sin i \cos\beta\cos\theta-\cos i\sin\beta}\right) \quad \text{又は}\qquad \text{方向角}=\cos^{-1}\left( \frac{\cos i \sin \beta -\sin i\cos \beta \cos\theta}{\cos (-50')} \right) \label{ho} \end{equation} 時刻の補正は \begin{align} & M_1=(\gamma-\alpha)+(\alpha-H_\gamma)\\ & H_\gamma=V\cdot(t-t_K)+\alpha_K\qquad V=0.98564736 \end{align} 経度による補正は \begin{equation} M_2=135-\text{その地点の経度} \end{equation} 日の出、日の入時刻は \begin{equation} \text{12時}+(\theta+M_1+M_2)\times \text{4分} \end{equation} となる。
第10章 計算例
試しに、名古屋での2012年1月4日の日の出日の入時刻を求めてみよう。
名古屋の経度は136.9167°、緯度は35.1667°である。
1月4日12時の\(\alpha\)を求める。式(\ref{t})を使い、近日点からの時間差\(\Delta t=\text{12時}-\text{8時42分}=\text{0.1375日}\)であるので \[ \alpha=\alpha_K+A_T(1+\cos 0)^2\Delta t=283.0006+0.1402=283.1408 \] となる(注 ちなみに私のプログラムでの計算では時間差分の式として \begin{eqnarray*} \varphi(t+\Delta t)&=&\varphi(t)+\frac{d\varphi}{dt}\bigg|_t \Delta t+\frac{1}{2}\frac{d^2\varphi}{dt^2}\Delta t^2\\ &=& \varphi(t)+\left(A(1+e\cos\varphi)^2(1-A(1+e\cos\varphi)e\sin\varphi\frac{\pi}{180}\Delta t)\right)\times \Delta t \end{eqnarray*} を使った。) 。次に1月4日12時の\(\beta\)を求める。式(\ref{seki})の\(\beta=\sin^{-1}(\sin K\sin \alpha)\)より\(\beta=-22.7911\)となる。 次に1月4日12時の\(\gamma\)を求める。式(\ref{seki})の\(\gamma=\tan^{-1}(\tan\alpha\cos K)\)より\(\gamma=284.2763\)となる。今は12時での\(\alpha,\beta,\gamma\)を求めたが、日の出、日の入時刻でも変わらないとして、日の出、日の入の時角\(\theta\)を求める。式(\ref{ji})をもう一度書くと \[ \theta=\cos^{-1}\left(\frac{\sin (\text{高度})-\sin i\sin \beta}{\cos i\cos\beta}\right) \] これより\(\theta=\pm 73.9343\)と求まる。これに4分を掛けると\(\pm\)4時間55.7分である。 日の出、日の入の方向角は式(\ref{ho})すなわち \[ \text{方向角}=\tan^{-1}\left(\frac{\cos\beta\sin\theta}{\sin i \cos\beta\cos\theta-\cos i\sin\beta}\right) \] から方向角=117.6°(日の出)、242.4°(日の入)と求まる。時刻の補正値は、\(\alpha,\beta\)が12時の値とほとんど変わらないとして、 \[ \gamma-\alpha=1.1355 \] \[ \alpha-H\gamma=A_T(1+e\cos 0)^2\Delta t-V\cdot \Delta t=0.00467 \] 合計で1.14017である。分に直すと1.14017×4分=4.6分である。経度による補正は \[ (135-136.9167)\times 4\text{分}=-7.7\text{分} \] よって日の出時刻は \[ \text{12時}-\text{4時55.7分}+\text{4.6分}-\text{7.7分}=\text{7時1分} \] 日の入時刻は \[ \text{12時}+\text{4時55.7分}+\text{4.6分}-\text{7.7分}=\text{16時53分} \] となる。 日の出は7時1分。その方向角は117.6°。日の入は16時53分、その方向角は242.4°となる。これは国立天文台の公表数値と一致する。尚2012年、1年分の計算結果は以下のグラフのようになる。
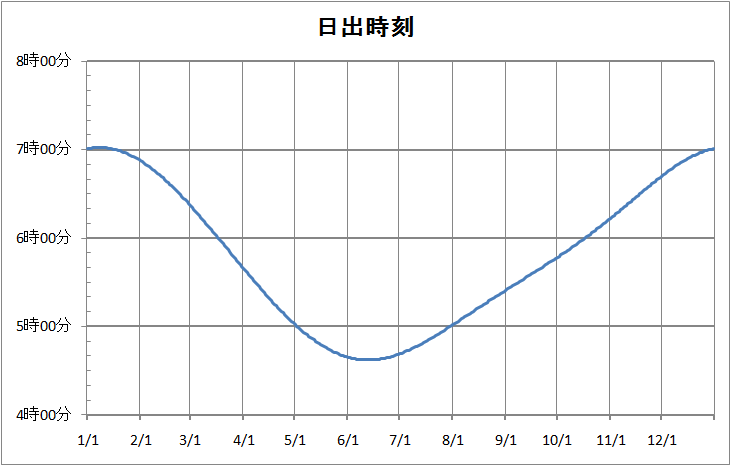
図10 2012年、名古屋市の日の出の時刻。
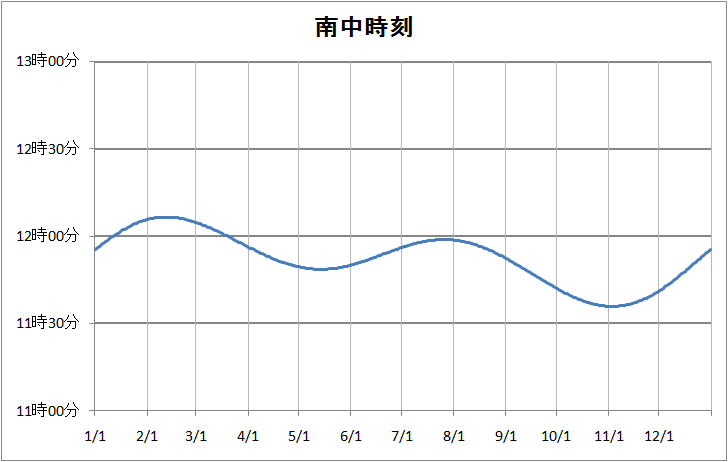
図11 2012年、名古屋市の太陽が真南に来る時刻。
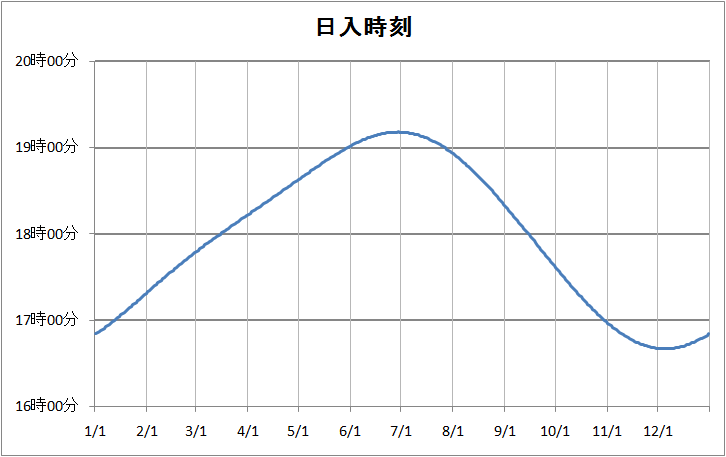
図12 2012年、名古屋市の日の入りの時刻。
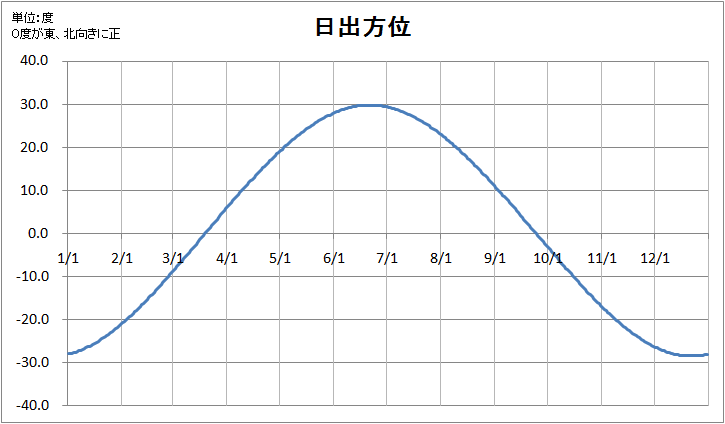
図13 2012年、名古屋市の日ので出の方位。真東を0°として縦軸が10なら北へ10°の方向で日の出と言う意味。
付録A 日の出日の入りの定義
日の出日の入りは太陽の上辺が見えた時刻としているようである。太陽の視半径は16'あるので中心が地平線から16'下がった位置で日の出となる(図14)。さらに大気の屈折も考えなければならない。地平線付近では光は34'屈折する。だから水平線上に見えているものは実は34'下にある(図15)。だらか太陽の視半径と合わせて50'。つまり太陽の中心が地平線の下、50'のところにあるとき日の出日の入となる。
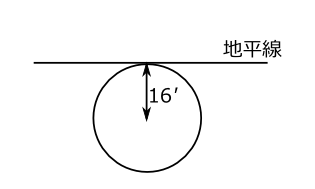
図14

図15