音波の方程式の導出
序論
この小論で空気中の音の波動方程式を導出する。空気というのは分子という小さい粒子が飛び回っているわけだが(図1)、これが波を伝えるというのは全く持って不思議なことである。ビー玉を箱に入れて片方の面を揺らしても決して波など発生しないだろう。単に個々のビー玉が玉突きのように衝突を繰り返すだけであろう。ただ、空気入ったのピストン(注射針のようなもの)を押すと反発し、引っ張ると引きかえされる。まるでピストンの中にバネがあるようである。バネが連なったものなら振動を伝えることは容易に想像つくであろう。風船をくっつけてつらねれば振動を伝えるであろう。音波の方程式の導出は四角い風船を互いに密着させたというイメージである(注1)。
音波の方程式は原子の存在の発見の前にニュートンによって導出されていたようである。ただ音速が実験値と合わないのでラプラスが音波の圧力変化は断熱変化としたらしい。そうすると実験値と合う音速となったようである。それで断熱変化でいいんだろうということになったようである。実験と合えばそれでよしという物理学の精神がよく表れている話だと思う。音波の方程式は空気を連続体としてみなして導出されたが実際は空気は連続体ではなく原子の集まりである。しかしとにかく実験と合う方程式があるのでそれ以上は何も追求しようとしないのであろう。それも物理学の精神をよく表わしていると思う。
導出
物理でよく使うことだが、まず微小な体積に着目し、それの運動を考える。音がない状態の微小体積\(\Delta V\)というものを考える。これは正方形で一辺を\(L\)とする(図2)。これはもちろん無限小量ということで極限として0に持っていく。この微小体積の質量は変わらないが体積は変化するとする。イメージとしては空気でなくゴムな様な物と考えた方がわかりやすいかもしれない。この微小体積要素が上下左右から圧力を受けて動くわけだが、その\(x,y,z\)方向の変位量をそれぞれ \[ h_x,h_y,h_z \] と書こう(図2)。音のないときの密度は \[ \rho \] と書こう。 この微小体積は圧力を受けて圧縮収縮をするわけだが、その体積の変化量を\(\delta V\)と書こう。すると体積変化率(単位体積当たりの体積変化量のこと)は \[ \frac{\delta V}{\Delta V} \] となる。音がないときの圧力からの、圧力の変化量を \[ p \] と書こう。これがいわゆる音圧である。これは無限小量ではない。つまり、量は小さいが極限で0にするわけではない。さてニュートンの運動方程式より微小体積の運動方程式は \begin{equation} \rho \ \ddot{\mathbf{h}} =-\nabla p \label{undou} \end{equation} となる。
不要かもしれないがこの式の導出法を書いておこう。\(x\)方向について考えよう。今の場合粘性をなしとする。するとこの微小体積に働く力は \[ [p(x_0)-p(x_0+L)](L +\delta y)( L+\delta z) \] である(注2) 。ここで注意だが、微小体積は自由に伸び縮みするし、位置もかわるのだが、この\(x,y,z\)座標も流体に合わせて、つまり流体に固定されて伸び縮みすると考えてもらいたい。\(\delta y\)というのはこの微小体積の\(y\)方向の変化量。\(L\)は無限小量だからこれは \[ -\left(\frac{\partial p}{\partial x}L+o(L)\right)(L +\delta y)(L+\delta z) \] となる。 さて、ここでだが\(\delta y\)というのは\(L\)と同位の無限小なのだが、音による体積変化は小さいとして、つまり\(L\)にくらべて圧倒的小さいとして無視する。すると上式は \[ -\frac{\partial p}{\partial x}L^3 \] となる。これが微小体積\(\Delta V\)にかかる\(x\)方向の力である。一方、微小体積\(\Delta V\)の質量は\(\rho \Delta V\)である。そして加速度は\(\ddot{h}_x\)である。というわけで式(\ref{undou})が導出されたわけである。
体積変化と変位との間には以下の関係が成り立つ。 \begin{equation} \frac{\delta V}{\Delta V}=\nabla \cdot \mathbf{h} \label{taiseki} \end{equation}
この式の導出はそう難しいことはなかろう。\(L\)が無限小であることと、\(\delta x,\delta y,\delta z\)が\(L\)に比して小さいということを使うわけである。体積増加量は(直方体に変形されると近似して) \[ (L+\delta x)(L+\delta y)(L+\delta z)-L^3 \] だが\(\delta x,\delta y,\delta z\)が\(L\)に比して小さいということを考慮して\(\delta\)の2次以上の項は無視して \[ \delta x L^2+\delta y L^2+\delta z L^2 \] と近似してしまう。\(\delta x\)は\(h_x(x+L)-h_x(L)\)であり、\(L\)は無限小量で高位の無限小量を無視すると \[ \frac{\partial h_x}{\partial x}L \] となる。というわけである。
次に圧力の増加は体積増加率に比例するとしてしまう近似をしよう。(こんな近似でいいかどうかは、要は何を知りたいかによると思う。) \begin{equation} \delta P=-K\frac{\delta V}{\Delta V} \label{atutai} \end{equation} ということである。\(K\)は断熱体積弾性率で\(K=P\gamma\)。\(\gamma\)は\(PV^{\gamma}=\text{定数}\)の\(\gamma\)のことである。\(\delta P\)は音圧\(p\)のことである。 以上上げた3つの 式\((\ref{undou}),(\ref{taiseki}),(\ref{atutai})\)を使って波動方程式を出す。\((\ref{undou})\)式の発散から \begin{equation} \rho(\nabla\cdot\ddot{\mathbf{h}})=-\triangle p \label{4} \end{equation} \((\ref{taiseki})\),\((\ref{atutai})\)から\(\delta V/\Delta V\)を消去して \begin{equation} \nabla\cdot \mathbf{h}=-\frac{1}{K}p \label{5} \end{equation} \((\ref{4})\),\((\ref{5})\)から\(\nabla\cdot \mathbf{h}\)を消去して、音圧の波動方程式 \[ \ddot p=\frac{K}{\rho}\triangle p \] を得る。音速\(c\)は \[ c=\sqrt{\frac{K}{\rho}} \] である。ちょっとこれを変形しよう。\(\rho=m/V\)として \[ c=\sqrt{\frac{K}{\rho}}=\sqrt{\frac{\gamma P}{\rho}}=\sqrt{\frac{\gamma P V}{m}}=\sqrt{\frac{\gamma nRT}{m}}\cong\sqrt{\frac{\gamma nRT_0}{m}}+\frac{1}{2}\sqrt{\frac{\gamma nR}{mT_0}}\Delta T \] 1気圧、0度を基準とすると \[ \gamma=1.40,\quad m=1.29kg,\quad n=\frac{1000}{22.4}\quad T=273 \] をいれると(体積は1m\(^3\)とした) \[ c=331.5+0.61\Delta T \] という計算しやすい式が出る。
吟味
今述べた導出法を少し反省してみよう。ここで使った近似法、すなわち実際は違うのだがそうだとして計算したものを列挙しよう。
- 気体に粘性はない(実際はあるが)
- 圧力は瞬間的に気体に伝わる(実際は時間がかかる)
- 音による体積変化は小さいので無視して計算してもいいときもある。
- 体積変化は小さいので単位体積変化率と圧力変化率は比例する(もちろん実際は比例しない)
- 体積変化は断熱変化である( 実際は熱は伝わる)
- 微小体積間に粒子数というか質量の変化はない。(実際は分子が移動することによって運動量を伝える、つまり圧力が変化するのである)
2の圧力が瞬間的に伝わってしまっては音速が無限大になってしまう。それなのに瞬間的に伝わるとして式を作って有限の音速値を導出させてしまうというのは不思議な話である。これは極限の取り方からの問題だろう。微小体積\(\Delta V\)は無限小に持ってくのでこの無限小体積の範囲内で圧力が瞬時に伝わるということである。もし無限小に持ってかなければ瞬間的に圧力は遠くまで達する。
音の方程式の導出は物理のモデルというものをよく表わしている。実際と異なる計算をしても煩雑で小さい者は無視して構成する。
実際の数値を列挙しよう。これは正弦平面波の場合である。音圧レベルSPL:60デジべルというのは普通の音の大きさらしい。これで音圧が0.02pa。大気圧が10万paだから、いかに小さいかがわかる。
| 名称 | 式 | 量 | 量 |
|---|---|---|---|
| 気体密度 | \(\rho\) | 1.29kg/m\(^3\) | 1.29kg/m\(^3\) |
| 音速 | \(c\) | 340m/s | 340m/s |
| 音圧レベル SPL | \(SPL=20\log_{10} \frac{p}{2\times10^{-5}} \) | 30デシベル | 60デシベル |
| 振動数 | \(\nu =2\pi \omega\) | 440Hz | 440Hz |
| 音圧 p |
\(p =2\times 10^{-5}\times 10^{\frac{SPL}{20}}\) (\(10^{\frac{1}{20}}=1.12\)) |
\(6.3\times 10^{-4}\) pa | 0.02 pa |
| 微小要素速度 |
\(v =\frac{p}{\rho c}\) (cは負の場合もあり) |
\(1.4\times 10^{-6}\)m/s | \(4.5\times 10^{-5}\)m/s |
| 変位 | \(h =i\frac{p}{\rho c\omega}\) | \(5.2\times 10^{-10}\) m | \(1.6\times 10^{-8}\) m |
| 体積変化率 | \(\frac{\delta V}{\Delta V}=\frac{p}{\rho c^2}\) | \(4.2\times 10^{-9}\) | \(1.3\times 10^{-7}\) |
平面音波の反射
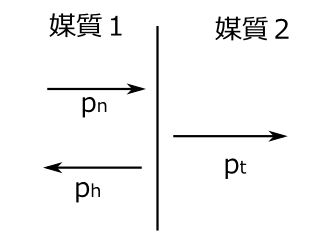
平面正弦波では \[ \frac{p}{\dot{h}}=\rho c \] が成り立つ。これは単に計算してみればすぐわかる。管の中の音波を考察しよう。いくつかの教科書などを読む限り、波長より管の直径が十分小さければ平面音波と考えていいようである。理由は特に書いていない。が、そうだと思おう。境界条件だが管のはじが閉じているときはそこでは体積速度\(\dot{h}\)は0としているようである。これはわかる。管のはじが全然振動しないような物質でできていればそうであろう。わからないのが管のはじが開いているときだが、どの教科書を見ても音圧を0としているところである。そして理由も書かれていない。急に広い所にでれば音圧が低下するというのは何となくわかるが。
一応反射率透過率というのは、境界で音圧と体積速度が等しいという境界条件から出てくる。 \[ \text{入射波}\quad p_n\exp i(wt-kx) \] \[ \text{反射波}\quad p_h\exp i(wt+kx) \] \[ \text{透過波}\quad p_t\exp i(wt-kx) \] として(図3)領域1の音響インピーダンスを \[ I_1=\rho_1 c_1 \] 領域2では \[ I_2=\rho_2 c_2 \] とすると \[ \frac{I_2-I_1}{I_1+I_2}p_n=p_h \] \[ \frac{2I_2}{I_1+I_2}p_n=p_t \] が成り立つ。導出は音圧と微小体積要素の速度が境界では等しいという条件からくる。
バネとの対応関係
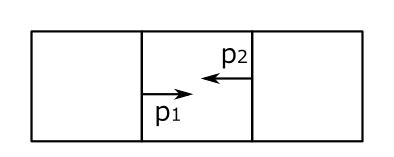
音の方程式は1次元のときは、バネの振動と全く対応している。それを表にしてみた。
|

|
| \[ \rho \Delta S \Delta x \ddot{h}=-p_2\Delta S+p_1\Delta S \] | \[ \rho\Delta x \ddot{h}=-F_2+F_1 \] |
| \[ p=-K\frac{\delta V}{V} \] | \[ F=-K\frac{\delta x}{\Delta x} \] |

|

|
| \[ \frac{\delta V}{V}=\frac{(h_2-h_1)\Delta S}{\Delta x \Delta S} \] | \[ \frac{\delta x}{\Delta x}=\frac{h_2-h_1}{\Delta x} \] |
断熱体積弾性率Kの導出
理想気体の準静的断熱過程での圧力と体積の関係は \[ PV^{\gamma}=\text{一定}\qquad \gamma=\frac{C_P}{C_V} \] である。断熱体積弾性率\(K\)は \[ K=P\gamma \] である。
その式の証明というか導出を書こう。
理想気体とは
1.内部エネルギーが温度のみに依存する
2.\(PV=nRT\)の関係が成り立つ。
ここで\(n\)はモル数、\(R\)は気体定数。
準静的過程では \begin{equation} dU+PdV=dQ \label{ki} \end{equation} である。準静的というのは、要は圧力が気体内部で均一になる速さで体積が変化するという意味である。だからピストンと気体の間に真空ができるほどの速さは準静的ではない。が、440Hzで振動する気体の変化は準静的ということのようである。
定積比熱は体積一定で一定温度上げるのにどれだけの熱量が必要かということである。この場合入ってきた熱はすべて内部エネルギーの増加となる。温度が\(dT\)上がる時の熱量は定義より\(C_VdT\)。これは内部エネルギーの増加量でもある。一方内部エネルギーは温度のみに依存しているので、温度が\(dT\)上がったときの内部エネルギーの増加量は、たとえ体積一定という制限がなくても\(C_VdT\)となる。
定積比熱と定圧比熱の関係
準静的過程では 準静的過程では \begin{equation} dU+PdV=dQ \end{equation} であり定圧過程では、定圧比熱の定義から \begin{equation} dU+PdV=C_pdT \label{teia} \end{equation} である。さらに退屈な式変形を続けていく。理想気体では \[ PV=nRT \] より \[ PdV+VdP=nRdT \] であり、定圧では \[ PdV=nRdT \] 式\(\ref{teia}\)に代入して、\(dU=C_VdT\)も代入すると \[ C_VdT+nRdT=C_PdT \] すなわち \begin{equation} C_P-C_V=nR \label{ju} \end{equation}