ローレンツ変換はなぜ線形変換でなければならないか
2011年7月25日
ある系で、2つの事象の時間・空間の座標差を測定したとしよう。その系に対して一定、一様な速度で動いている系で、その2つの事象の時間・空間の座標差を測定したとしよう。このとき、この2つの系で測った時間と空間の座標差の関係式(いわゆるローレンツ変換)は時間空間に関して1次式でなければならない。このことは、時間空間の一様性からの当然の帰結である。アインシュタインの原論文(「相対性理論」 アインシュタイン著 内山龍訳 岩波文庫 1988年、「アインシュタイン選集1」 中村孝太郎訳 共立出版 1971年)では”空間時間が一様のため”(注 アインシュタイン 「相対性理論」 内山龍雄訳 岩波文庫 27ページ 「まず第1に、空間および時間が持っているものと考えられる一様性のために、求める関係式は1次式でなければならないということは明白といえよう」とある。又、別の訳では、アインシュタイン選集 第1巻 中村誠太郎訳 共立出版 26ページ 「第1に、これらの方程式は1次でなければならない。なぜならば空間と時間は斉一という性質をもつと仮定したからである。」とある。少し訳が違うが、私は内山の訳は少し意訳しているのではと想像している。)の一言で片づけられていて正にその通りなのである。ただ、その一言ではわかりずらいので、この小論文で、時間空間の測定の関係式がなぜ一次式(線形)でなければならないかを解説する。この解説では簡単のため、空間は\(x\)座標のみとする。
目標は任意の2つの事象をある系(今後、静止系と呼ぼう)で測った空間・時間の差\((\Delta x,\Delta t)\)と静止系に対して一定一様の速度で動いている系(今後、動系と呼ぼう)で測った\((\Delta x',\Delta t')\)との関係式が1次式、すなわち \begin{eqnarray*} \Delta x'= & a \, \Delta x+b \, \Delta t\\ \Delta t'= & c \, \Delta x+d \, \Delta t \end{eqnarray*} でなければならないということを示すことである。ここで\(a,b,c,d\)は\(x,t\)に依存しない定数である。
第1章 変換が位置、時刻に依存しないこと
今、例えば図1のように静止系の\(x\)軸上にAさん、Bさん、Cさんが3mずつ離

図1 Aさん、Bさん、Cさんが1直線上に3m間隔で並び2秒置きに手をたたく事象。
れて並んでいるとする。そして、まずAさんが手をたたいたとして、2秒後に今度はBさんが手をたたいたとし、そのまた2秒後にCさんが手をたたいたとする。すなわち、Aさんが手をたたいてからBさんが手をたたくまでの事象差は \((\Delta x,\Delta t)=(3\text{m},2\text{秒})\)である。 Bさんが手をたたいてからCさんが手をたたくまでの事象差も\((\Delta x,\Delta t)=(3\text{m},2\text{秒})\)である。 このとき動系でこれらの事象差を測ったとき Aさんが手をたたいてからBさんが手をたたくまでの事象差が例えば\((\Delta x',\Delta t')=(5\text{m},3\text{秒})\)であったとしよう。 すると、Bさんが手をたたいてからCさんが手をたたくまでの事象差は 空間・時間は一様なので当然\((\Delta x',\Delta t')=(5\text{m},3\text{秒})\)となるはずである(図2)。空間・時間に特別な点は存在しないからである。すなわち、ある地点、

図2 動いている系から見た図
ある時間においての2つの事象差が静止系で\((3\text{m},2\text{秒})\)であり、それを動系で測ると\((5\text{m},3\text{秒})\)であったなら、別の地点、別の時刻における2つの事象差が静止系で\((3\text{m},2\text{秒})\)である場合、動系で測ると同じ\((5\text{m},3\text{秒})\)となる。すなわち、 変換則は場所、時刻に依存しない。 このことから、変換が1次変換でなければならないことが導出される。
第2章 1次式の導出
今、静止系において事象差\((1\text{m},0\text{秒})\)、すなわち、同時で1m離れた事象を動系で測ったとき例えば(2m,1秒)だったとしよう。又、静止系において事象差(0m,1秒)、すなわち同じ位置で時間が1秒後に起きる事象を動系で測ると例えば(3m,4秒)だったとしよう。まとめると \begin{equation} (1\text{m},0\text{秒})\Longrightarrow (2\text{m},1\text{秒})\quad (0\text{m},1\text{秒})\Longrightarrow (3\text{m},4\text{秒}) \label{settei} \end{equation} と変換されると設定しとくということである。
2-1節 \(\Delta x,\Delta t\)が正の整数の場合
この設定のもと\(\Delta x,\Delta t\)が正の整数の場合、どう変換されるかを考えよう。そこで何でもいいのだが、例えば静止系の事象差(3m,2秒)が動系でどう変換されるかを調べよう。 (3m,2秒)という事象差は、Aさん、Bさん、Cさん、Dさんが\(x\)軸上に1mづつ離れてならび、同時に手をたたく。そして、その1秒後にDさんが手をたたく、さらに、その1秒後にDさんが手をたたくという事象に分解できる(図3,4)。AさんとBさんが手をたたく事象差は静止系

図3

図4
では(1m,0秒)なので動系で測ると設定より(2m,1秒)である。同様にBさんとCさんが手をたたく事象差は静止系では(1m,0秒)、動系では(2m,1秒)である。CさんとDさんが手をたたく事象差も同様である。一方Dさんが最初に手をたたいてから1秒後に手をたたく事象差は静止系では(0m,1秒)なので動系で測るとは設定より(3m,4秒)である。同様にDさんが2回目に手をたたいててから3回目に手をたたく事象差は静止系では(0m,1秒)なので動系では

図5
(3m,4秒)である(図5)。これをまとめると \[ \begin{array}{cccl} &(1\text{m},0\text{秒})&\Longrightarrow&(2\text{m},1\text{秒})\\ &(1\text{m},0\text{秒})&\Longrightarrow&(2\text{m},1\text{秒})\\ &(1\text{m},0\text{秒})&\Longrightarrow&(2\text{m},1\text{秒})\\ &(0\text{m},1\text{秒})&\Longrightarrow&(3\text{m},4\text{秒})\\ +&(0\text{m},1\text{秒})&\Longrightarrow&(3\text{m},4\text{秒})\\ \hline \text{合計}&(3\text{m},2\text{秒})&\Longrightarrow&3\times (2\text{m},1\text{秒})+2\times (3\text{m},4\text{秒}) \end{array} \] となる。つまり静止系の(3m,2秒)は動系では \[3\times (2\text{m},1秒)+2\times (3\text{m},4秒)\] と変換される。今の例では\(\Delta x=3,\Delta t=2\)としたが、\(\Delta x,\Delta t\)が任意の正の整数の場合でも、まったく同じように考えれば(\(\Delta x\)m,\(\Delta t\)秒)が \[\Delta x\times (2\text{m},1秒)+\Delta t\times (3\text{m},4秒)\] に変換されることがわかる。すなわち \begin{eqnarray*} \Delta x'= & 2\text{m} \, \Delta x+3\text{m} \, \Delta t\\ \Delta t'= & 1\text{秒} \, \Delta x+4\text{秒} \, \Delta t \end{eqnarray*} となる。これが、変換が1次式になる本質的な理由である。
2-2節 \(\Delta x,\Delta t\)が正の分数の場合
次に\(\Delta x,\Delta t\)が正の分数の場合を考える。例として(2/3m、3/5秒)がどう変換されるかを考えよう。これは、先に記した(3m、2秒)の分解と同じように考えて、 \begin{eqnarray} (2/3\text{m},3/5秒) &= &(2/3\text{m},0\text{秒})+(0\text{m},3/5{秒})\notag \\ &= & (1/3\text{m},0\text{秒})+(1/3\text{m},0\text{秒})+ (0\text{m},1/5\text{秒})+(0\text{m},1/5\text{秒})+(0\text{m},1/5\text{秒})\notag \\ &= & 2\times (1/3\text{m},0\text{秒})+3\times (0\text{m},1/5\text{秒}) \label{1} \end{eqnarray} と分解される。そこで、事象差(1/3m,0秒)と(0m,1/5秒)が動系でどう測定されるかがわかればよい。(1/3m,0秒)を考えよう。今、静止系で Aさん、Bさん、Cさん、Dさんの4人が1/3mづつ離れて並んでいて、この4人が同時に手をたたくという状況を考えよう(図6)。静止系では隣どうしの人が手を
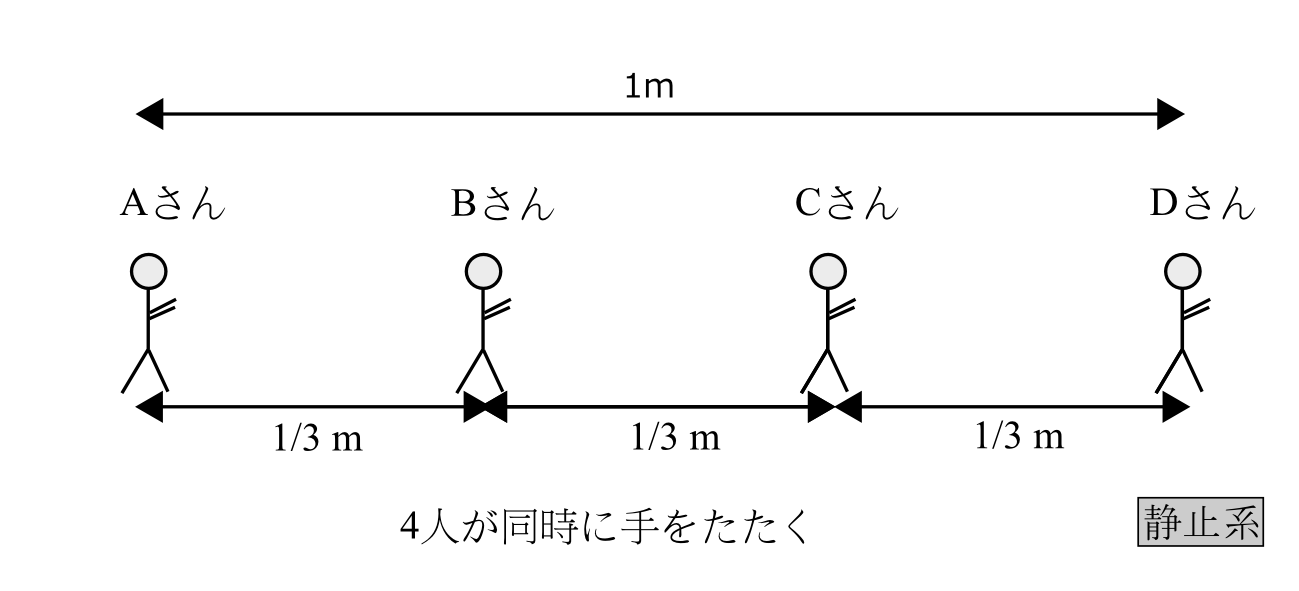
図6
たたく事象差は(1/3m,0秒)だが、動系では(\(a\)m,\(b\)秒)だったとしよう。この\(a,b\)の値を知りたいわけである。Aさんが手をたたいたという事象から、Dさんが手をたたいたという事象までの事象差は、静止系では(1m,0秒)であり、動系では3\(\times\)(\(a\)m,\(b\)秒)となる(図7)。一方、設定より静止系での

図7
(1m,0秒)は動系では(2m,1秒)に変換される。したがって \[ 3\times(a\text{m},b\text{秒})=(2\text{m},1\text{秒}) \] でなければならない。すなわち \[ (a\text{m},b\text{秒})=\frac{1}{3}(2\text{m},1\text{秒}) \] と\(a,b\)が求まる。今わかったことは、もし \[ (1\text{m},0\text{秒})\Longrightarrow (2\text{m},1\text{秒}) \] と変換されるなら、 \[ (1/3\text{m},0\text{秒})\Longrightarrow \frac{1}{3}\times (2\text{m},1\text{秒}) \] と変換されるということである。(0m,1/5秒)に関しても同様に考えて \[ (0\text{m},1\text{秒})\Longrightarrow (3\text{m},4\text{秒}) \] と変換されるなら \[ (0\text{m},1/5\text{秒})\Longrightarrow \frac{1}{5}\times (3\text{m},4\text{秒}) \] と変換される。式(\ref{1})に戻ると \begin{eqnarray*} \left(\frac{2}{3}\text{m},\frac{3}{5}\text{秒}\right)\Longrightarrow & 2\times\left( \frac{1}{3}\times(2\text{m},1\text{秒})\right)+3\times \left(\frac{1}{5}\times(3\text{m},4\text{秒})\right)\\ & = \left( \frac{2}{3}\times(2\text{m},1\text{秒})\right)+ \left(\frac{3}{5}\times(3\text{m},4\text{秒})\right) \end{eqnarray*} と変換される。今の例では\((\Delta x,\Delta t)=(2/3,3/5)\)としたが、同じように考えれば\(\Delta x,\Delta t\)が任意の正の分数で\((\Delta x,\Delta t)\)が \[\Delta x\times (2\text{m},1秒)+\Delta t\times (3\text{m},4秒)\] と変換されるのは明白であろう。すなわち \begin{eqnarray*} \Delta x'= & 2\text{m} \, \Delta x+3\text{m} \, \Delta t\\ \Delta t'= & 1\text{秒} \, \Delta x+4\text{秒} \, \Delta t \end{eqnarray*} となる。
2-3節 \(\Delta x,\Delta t\)が負の整数、分数の場合
\(\Delta x\)又は\(\Delta t\)が負の整数又は分数の場合を考える。無理数の場合は考えない。例として\((-2\)m\(,-3\)秒)がどう変換されるかを考えよう。これは今までと同様に考えて \[ (-2\text{m},-3\text{秒})=(-2\text{m},0\text{秒})+(0\text{m},-3\text{秒}) \] と分解される。まず(0m,\(-3\)秒)を考えよう。さて、Aという事象から見てBという事象への事象差が(0m,\(-3\)秒)であるということは、Bという事象から見て、Aという事象への事象差が(0m,3秒)であるという意味である。今までの議論より(0m,3秒)は動系では\(3\times\)(3m,4秒)に変換される。これはBという事象から見てAという事象が動系では\(3\times\)(3m,4秒)と測定されるという意味である。ということは動系でAという事象から見て、Bという事象への事象差は \[ -(3\times (3\text{m},4\text{秒})) \] だということである(模式図8)。(\(-2\)m,0秒)に関しても同様に考えればよ
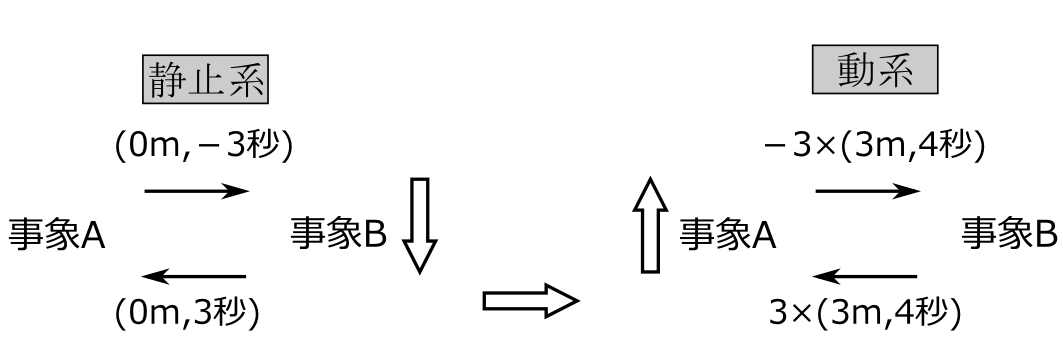
図8
い。すると(\(-2\)m,\(-3\)秒)は \[ -2\times(2\text{m},1\text{秒})-3\times (3\text{m},4\text{秒}) \] と変換される。\(\Delta x\)と\(\Delta t\)が\((-3,4)\)や\((4,-5)\)や\((10,-100)\)でも同じように考えればよい。それで\(\Delta x,\Delta x\)が任意の有理数で\((\Delta x,\Delta t)\)が \[\Delta x\times (2\text{m},1秒)+\Delta t\times (3\text{m},4秒)\] と変換されるのは明白であろう。すなわち \begin{eqnarray*} \Delta x'= & 2\text{m} \, \Delta x+3\text{m} \, \Delta t\\ \Delta t'= & 1\text{秒} \, \Delta x+4\text{秒} \, \Delta t \end{eqnarray*} となる。 以上がローレンツ変換がなぜ線形でなければならないかの理由である。尚、\(\Delta x,\Delta t\)が無理数の場合は、物理では考えなくてよい。分数でいくらでも近似できるからである。今は式(\ref{settei})のように設定したが、一般に静止系の\((1\text{m},0\text{秒}),(0\text{m},1\text{秒})\)がそれぞれ動系で \begin{equation} (1\text{m},0\text{秒})\Longrightarrow (a\text{m},c\text{秒})\quad (0\text{m},1\text{秒})\Longrightarrow (b\text{m},d\text{秒}) \end{equation} と変換されるなら、\((\Delta x,\Delta t)\)は、 \begin{eqnarray*} \Delta x'= & a\text{m} \, \Delta x+b\text{m} \, \Delta t\\ \Delta t'= & c\text{秒} \, \Delta x+d\text{秒} \, \Delta t \end{eqnarray*} と変換される。以上でこの論文を終える。ここでの説明は算術の説明に似ているところがある。例えば、なぜ\(3\times 4=4\times 3\)なのか。なぜ\((3\times 4)\times 5=3\times (4 \times 5)\)なのかを説明するのに似ているところがあると感じた。