光の軌跡の変換としてのローレンツ変換
2011年6月28日
第1章 時間
1.1節 時間について
この論文では、時間というものを光の運動すなわち光の移動した距離と定義してローレンツ変換を考察する。すなわち、ある地点から光が発せられ、例えば距離3m離れた地点に到達したとすると、光が発せられてから到達したまでの時間を"3"と定義するのである。もちろん変換のための比例定数を掛けてもよいが(係数として例えば"2"としたらこの時間は2×3で6とする)本質的なことではないので考えないことにする。
なぜこのように時間を定義するのかというと 我々の時間についての感覚、概念をより恒久的な剛体上の距離に還元したいからである。物理学では様々な概念を剛体上の長さに還元してきた。力、運動量、エネルギー、電気量などを考えてみればわかる。これは、測定というものは普通目盛を読むということからも明らかであろう。なぜ物理量を剛体の長さに還元する方法をとってきたかを明確に述べるのは難しいが、長さの関係が時間に依存せず不変なこと、すなわち、ある物体と別の物体がぴったり重なるなら、別の日もぴったり重なること。それと、この重なるというのが誰が見ても意見が一致するからであろう。これが例えば、熱いという感覚では、ある人はAとBは同じ熱さだといっても別の人はAの方が熱いということはよくあることだ。又、ある人が2つの物体AとBを持って、Aの方が重いと感じても別の人はBの方が重いと感じることもある。
時間の概念を長さに還元することは、実は我々人類が行ってきたことである。我々は地球の1回の自転を1日としてきた。すなわち、太陽の天球上の移動した長さを時間に使ってきた。古くは水時計が使われてきたが、これは水が減った量すなわち長さの3乗を時間として使ってきた。
時間というものは基準運動の回数のことである。基準運動は地球の自転であったり、水時計の水量の変化などがその例である。又、別の言葉で言えば時間というものは運動の回数の比のことである。我々は、この比が過去も未来も一定であるということを経験上知り、数としての時間概念を得てきたのであろう。数というものは共通な性質を持ったものの個数のことである。例えばみかん3個というのは、みかんという共通な性質をもったものが3つあるという意味であり、果物3個というときは、果物という性質をもったものが3つあるという意味である。時間の場合で言えば、今日、砂時計の1回が水時計の2回に対応していたら、明日も砂時計の1回が水時計の2回に対応する事実を知り、我々は昨日の砂時計1回分と今日の砂時計1回分は同じだとして時間を数えられるものと認識したのであろう。
単純な現象の運動どうしの比は一定である。振り子時計と砂時計の運動の比はほぼ一定であろうが、我々は経験上空気圧などで、これらの比が多少変化することを知っており、この2つの時計は真の時間を表わしていないことを知っている。ただこの「真の」というのは少し微妙な概念であり、より比が一定に保たれるものといってもいいかもしれない。今日は光の1往復が電子の2往復に対応し、次の日は光の1往復が電子の3往復に対応するというのは過去と未来で物理法則が異なり我々の信念に反する。そういう意味で確率的な量子力学は我々の信念又は時間の一様性に反することになる。電子ビームが今日は電子10個スリットを通り抜け明日は3個というのは時間に関して対称ではない。我々はもし光と電子の運動の比が昨日と今日で異なれば、これは昨日と今日では異なる運動であり、原因を探るであろう。振り子時計が空気の摩擦によって一振動ごとに異なる運動をしていると推測するように。
時間の定義として、基準運動は光に限られない。どんな運動でも繰り返し同じ運動が行われればよいのである。振り子時計の場合、空気抵抗によって振動を重ねるごとに減衰し、厳密には一回目の往復と二回目の往復は同じ運動ではない。又振り子を構成している原子が多数あり、個々の原子の運動を見れば、一往復目と二往復目では全然違う運動であろうから振り子が同一の運動をしているとはいえない。ただし統計力学的にマクロでみれば同一の運動と見てよい。そういう意味で、時計としては、それを構成している粒子の数が少ない方がいいと言えるだろう。現在は原子時計が最も精密といわれているようだが、これとて程度の問題であろう。原子の内部には原子核があり、個々の陽子や中性子はいつも同じ運動をしているわけではないからである。
1.2節 時間の定義
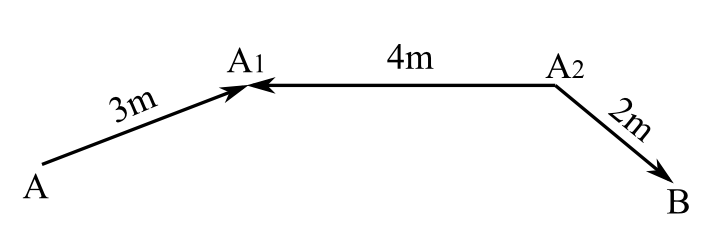
図1.1
時間は最初に述べたように、光の移動距離で定義するわけだが、ここで正確に述べよう。まず例で考えよう。点AでAさんが、点BでBさんが手をたたいたとしよう。その事象をそれぞれA(J)、B(J)と呼ぼう。図1.1のように事象A(J)と同時に点Aから光を発し、点A\(_1\)に着いたとしよう。それと同時に点A\(_2\)から発せられた光が点A\(_1\)に着いたとしよう。点A\(_2\)からは点A\(_1\)に光が発せられたとの同時に点Bに光が発せられ、事象B(J)と同時に点Bに着いたとしよう。各点間の距離は \[ \text{AA}_1=3\text{m}\quad \text{A}_1\text{A}_2=4\text{m}\quad \text{A}_2\text{B}=2\text{m} \] だったとしよう。この場合、事象A(J)が起きてから事象B(J)が起きるまでの時間はどう定義すればよいだろうか。これは時間の普通の考え通り、事象A(J)から点A\(_1\)での事象までの時間差は"3"、点A\(_1\)での事象から点A\(_2\)までの時間差は"\(-4\)"、点A\(_2\)での事象から事象B(J)までの時間差は"2"、合計すると \[3-4+2=1\] すなわち事象A(J)から事象B(J)までの時間差は"1"と考えればよい。同様に事象B(J)から事象A(J)までの時間差は \[-2+4-3=-1\] で"\(-1\)"と考えればよいのである。つまり符号が逆になるということである。では、この例を一般化して時間の定義を正確に述べよう。
時間の定義: ある事象から、別の事象への時間差は、その2つの事象を光の経路で表わして、光の経路がこの経路の向きと同じ部分は、その距離を、光の進行方向が経路の向きと逆の部分は、その距離にマイナスをつけたものを全て足し合わせたものである。
ここで、いくつか言葉を定義しておこう。 光の経路とは上で例示したように折れ点では、隣り合う光の軌跡が同時に光の放出、又は到着が起きているものを指すとする。 2つの事象を光の経路で表わすとは、光の経路の始点と終点で光の放出、又は到着という事象と、この2つの事象がそれぞれ同時に起きているということである。 今後もこの意味で使う。尚、会合するとは、2つの事象が同じ位置で同時に起きることである。
1.3節 全ての事象の時間を表わせること
今述べた方法でどんな2つの事象の時間差も表わすことができるということを示そう。A地点でAさんが手をたたいた。その後、別の場所B地点でBさんが手をたたいた。この2つの事象を光の経路で表わしてみよう。 Aさんが手をたたいたとき、点Aから点Bに向けて光を発する。Bさんが手をたたいたときも点Bから点Aに向けて光を発するとする。

図1.2
間で会合する場合
光が点Aと点Bの間で会合したとしよう。 例えば図1.2(a)のように点Aから4m、点Bから2mの地点で会合したとする。この場合Aさんが手をたたいてから、Bさんが手をたたくまでの時間差は \[4-2=2\] である。
点Bで会合する場合
次に、点Aからの光が点Bに到達したときと同時にBさんが手をたたいた場合を考えよう。この場合はAからBの距離がそのままAさんが手をたたいてからBさんが手をたたくまでの時間差になる(図1.2(b))。
光が到達したとき、まだBさんが手をたたいていない場合
最後に点Aからの光が点Bに到達したとき、まだBさんが手をたたいていない場合を考える。この場合点Aからの光は点Bを通り過ぎて、Bさんが手をたたいたときに点Bに着くような点で折り返してもらう。図1.2(c)の場合なら 点Aから発せられた光は点Bを通り過ぎ8m進んだときに折り返し、2m戻って点Bに着き、そのときBさんが手をたたいたとするとAさんが手をたたいてからBさんが手をたたくまでの時間は \[8+2=10\] である。このように、どんな2つの事象でも光の移動した距離を足したり引いたりすれば、その時間差を計算できることがわかった。すなわち
命題1 どんな2つの事象も、その事象が起きた点を結んだ直線上の光の経路で表わすことができる。
1.4節 時間の定義が一意なこと
さて、このように光の移動距離で2つの事象の時間差を定義することができるためには、2つの事象の時間差はどんな光の経路で測っても等しくなければならない。例えば図1.3のように点A、点Bで起きた事象を2つの経路で
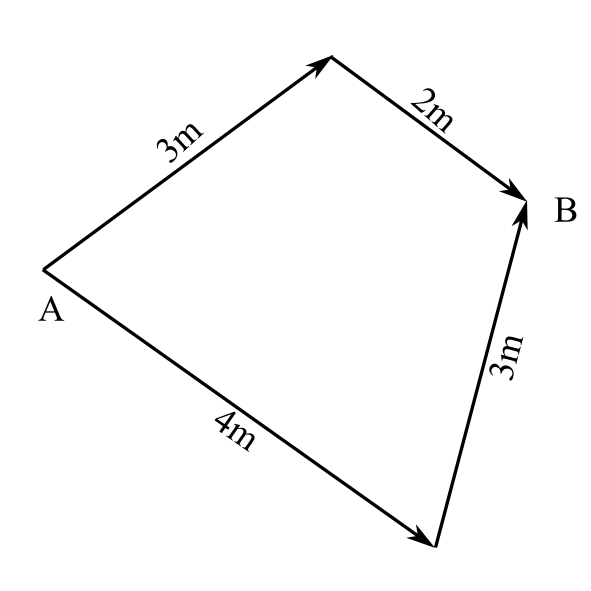
図1.3
測ったとき、一方では\(3+2=5\)、もう一方では\(4+3=7\)となってはならないということである。それゆえ光は次のような性質を満たしている必要がある。
会合の原理:
ある地点Aから光を2つの方向に同時に発し、その光が別々の経路を通って、ある同じ地点Bに到達したとき
(a) 2つの経路の距離が等しいなら光は会合し、つまり同時に着き
(b) 距離が異なるなら会合しない、つまり同時に着かない
もし、今考えている系が空間的に等方だとしたらなら、そして光の速さが放出体の運動に依存しないなら、当然この会合の原理が成り立つであろう。ある方向へ進む光の速さの方が別の方向に進む光の速さよりも大きいとは考えづらいからである。ここで強調したいことは、光の速さがどの方向にも一定であるということは決して規約の問題ではないということである。光の移動距離で時間を定義すれば確かに光速はどの方向にも一定であり規約の問題だが、それだけでなく会合の原理を満たすという物理的事実があるのである。空気に対して動いている系で音波の移動距離を時間の定義に使うとしたら、音速はどの方向にも一定となるが、これは単なる規約である。音波は会合の原理を満たさず、音波の経路によって、事象間の時間差が異なってしまう。光速がどの方向にも一定であるということは、物理的にはこの会合の原理と同等であると私は考えている。実際のところ同等というよりも、光速がどの方向に対しても一定であるということの、より正確な表現ではないだろうか。
ところで、上記会合の原理だけでは2つの事象の時間差はどんな光の経路で測っても等しくなければならないということを満たすには不十分に見える。なぜなら、時間差を測るには当然、経路の中に経路の向きに逆行している部分を含んでいる光の経路も考慮に入れなければならないからである。例えば、図1.4のように点A、点Bで起きた事象を2つの経路で測ったとき、一
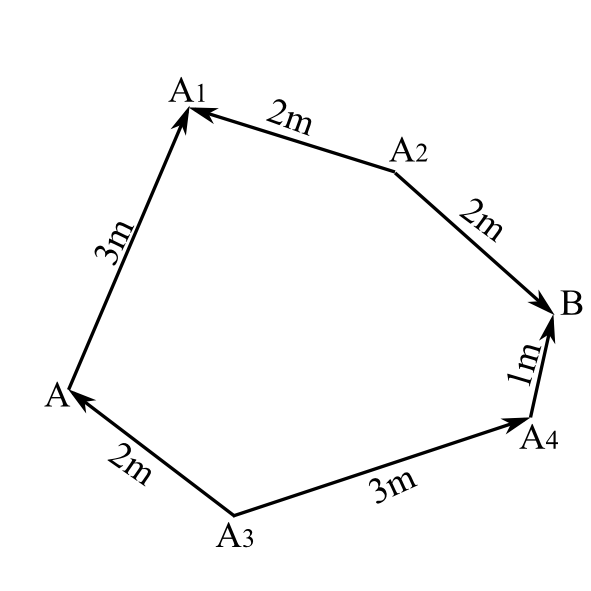
図1.4
方では\(3-2+2=3\)、もう一方では\(-2+3+1=2\)というように異なってはならないのである。それゆえ、光は次のような性質を満たす必要がある。
第2会合の原理:
始点での事象が会合しており、終点の位置が等しい2つの光の経路は
(a) その経路の時間的距離が等しいなら終点で会合し
(b) 等しくないなら会合しない
ここで、あいまいさを防ぐために言葉の意味を明確にしておこう
時間的距離とは、その経路で測った時間差のことである。つまり点Aから点Bへの光の経路の時間的距離とは、光が点Aから点Bへの方向に進むなら、その距離、点Aから点Bへの方向と光が逆行しているなら、その距離にマイナスをつけて、全ての直線について足したものである。図1.4の光の経路A\(\rightarrow\) A\(_1\rightarrow\) A\(_2\rightarrow\) Bの時間的距離は\(3-2+2=3\)である。
始点で会合しているとは、図1.4の場合だと、点Aから点A\(_1\)へ光を発するのと点A\(_3\)から発せられた光が点Aに着くのが同時であるということであり、終点で会合しているとは点A\(_2\)からの光が点Bに着くのと点A\(_4\)からの光が点Bに着くのが同時であるということである。定義終わり 。今後もこの意味で使う。
第2会合の原理は会合の原理を含んでおり、より一般的に光の運動について述べているのである。この第2会合の原理も空間が等方的であり、そして光の速さが放出体の運動に依存しないなら、当然成り立つと考えられる。ただ単に表現のしかたが会合の原理よりも、もってまわった言い方をしているだけである。実際のところは、会合の原理の(a)、会合の原理の(b)、第2会合の原理の(a)、第2会合の原理の(b)という4つの原理は物理的に当然の事実を入れれば同等であるということが証明できる。ただ、それは少し話のすじがそれるので付録A.1で述べることにした。読者は最もイメージしやすい表現である2つの経路の距離が等しいならば光は会合するという会合の原理(a)を頭にいれてもらえればよいと思う。尚、この会合の原理は、時間空間が現代数学でいる線形空間であることに対応すると考えられる。少し不正確な表現が許されるならば、この会合の原理は、ある位置、ある時刻における時間差が例えば"3"であるということは、別の位置、別の時刻における時間差が"3"であることと同等であるということを言っているのであろう。
ところで、光速がどの系でも同じ値であるというのは、この会合の原理以上のことを主張している。これは一方の系で、ある砂時計1回分が光が2m進むのに対応していたなら、もう一方の系でも、その同じ砂時計1回分が光が2m進むのに対応する、ということも主張しているのである。光がそういう性質を持っているからこそ時間の定義に使えるのである。