光の軌跡の変換としてのローレンツ変換

2011年6月28日

付録A

A.1 会合の原理と第2会合の原理の同等性の証明

A.1.1 (a)と(b)の同等性

　この付録で会合の原理(a)、(b)、第2会合の原理(a)、(b)という4つの原理の同等性を証明する。まず会合の原理(a)と(b)の同等性を証明しよう。会合の原理をここに再掲すると

(a)\(\rightarrow\)(b)の証明

例えば経路(1)の方が経路(2)より距離が短かったとしよう。経路(1)の光は終点Bに着いた後、経路(2)と距離が等しくなるように、寄り道して終点Bに戻ってきてもらおう。すると会合の原理(a)より、寄り道後に、経路(2)の光と会合する。ということは寄り道前には会合しなかったということである。証明終
(b)\(\rightarrow\)(a)の証明
経路(1)と経路(2)の距離が等しいのに、経路(1)の光が先に終点Bに着いたとしよう。それなら、経路(1)の光に寄り道してもらい、ちょうど経路(2)の光が終点に着く時に戻ってきてもらおう。すると、経路(1)の光は寄り道した分だけ経路(2)より長いのに終点で光は会合する。これは会合の原理(b)に反する。ということは、距離が等しいときは会合するということである。証明終

次に第2会合の原理(a)、(b)の同等性を証明する。証明法は今の場合と全く同じである。第2会合の原理をここに再掲すると

(a)\(\rightarrow\)(b)の証明　例えば経路(1)の方が経路(2)より時間的距離が小さかったとしよう。経路(1)の終点での事象の後、経路(2)の時間的距離が等しくなるように、寄り道して終点Bに戻ってきてもらおう。すると第2会合の原理(a)より、寄り道後に、経路(2)の光と会合する。ということは寄り道前には会合しなかったということである。証明終
(b)\(\rightarrow\)(a)の証明
経路(1)と経路(2)の時間的距離が等しいのに、経路(1)の終点の事象の方が先に起きたとしよう。それなら、経路(1)の光に寄り道してもらい、ちょうど経路(2)の終点での事象が起きるときに戻ってきてもらおう。すると、経路(1)の光の時間的距離は寄り道した分だけ経路(2)より長いのに終点で光は会合する。これは第2会合の原理(b)に反する。ということは、時間的距離が等しいときは会合するということである。証明終

A.1.2 会合の原理を使って第2会合の原理の証明

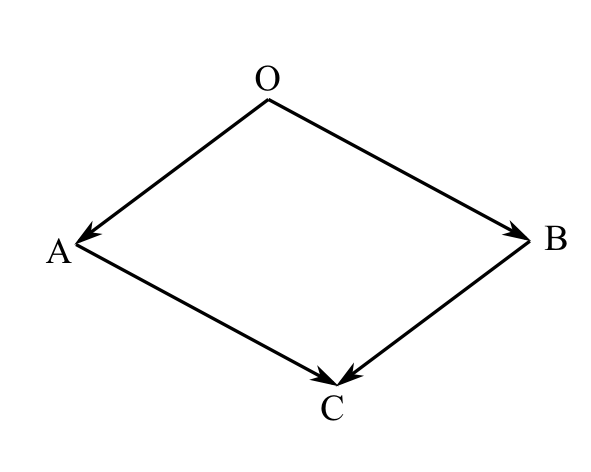
図A.1

　会合の原理から第2会合の原理を証明するために、1つの補題について述べよう。 2つの事象A(J)、B(J)が図A.1のように光の経路A\(\rightarrow\)O\(\rightarrow\)Bで表わせたとしよう。光はAOでは経路に逆行し、OBでは順行していたとしよう。今、点Cを四角形OACBが平行四辺形になるようにとろう。事象A(J)と同時に光を点Aから点Cに発し、事象B(J)と同時に光を点Bから点Cに発するとしよう。O\(\rightarrow\)A\(\rightarrow\)CとO\(\rightarrow\)B\(\rightarrow\)Cは距離が等しいので、会合の原理(a)より、光は点Cで会合する。つまり、このA(J)、B(J)という事象は光の経路A\(\rightarrow\)C\(\rightarrow\)Bで表わせるということである。軌跡の逆行と順行の順で構成されている光の経路は、各光の軌跡の向きと長さを変えないで順序を入れ替えて作った順行と逆行の順で構成されている光の経路で表わすことができるということである。又、その逆の順行と逆行の順で構成されている経路も順序を入れ替えた逆行と順行の軌跡で表わせるということでもある。又、会合の原理(a)より、順行と順行の順で構成されている経路の順序入れ替えも可能であり、逆行と逆行の順序を入れ替えることも可能である。以上より

といえる。

　さて、この補題を使って会合の原理から第2会合の原理を証明しよう。今、2つの事象が2つの光の経路で表わせたとしよう。簡単のため、その経

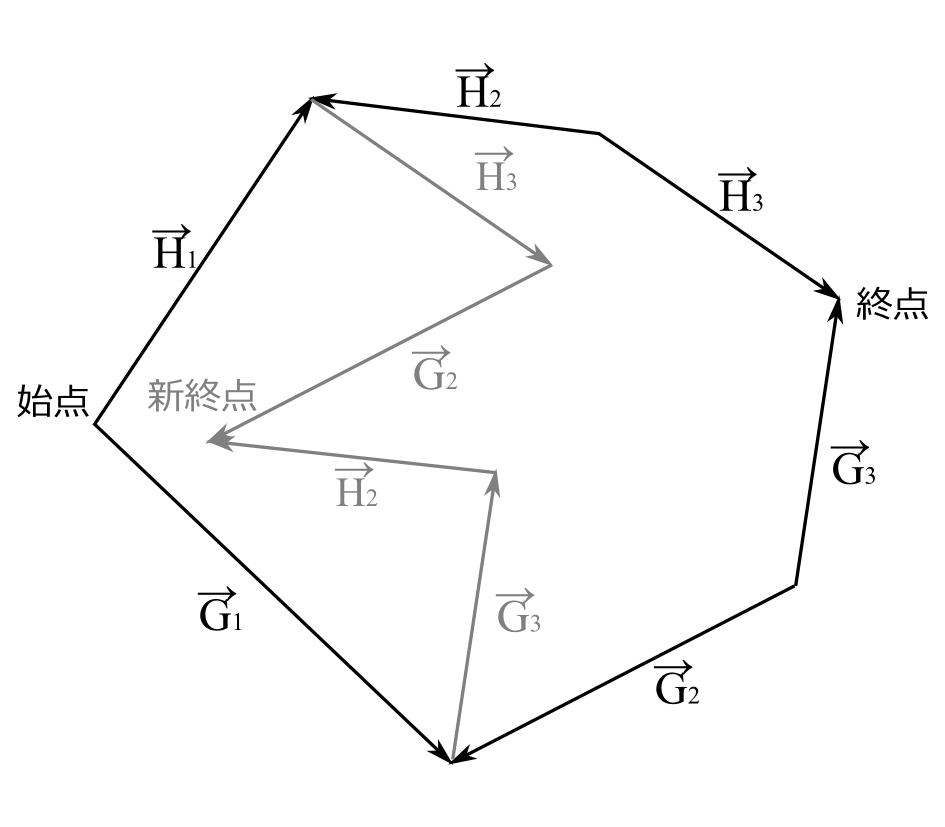
図A.2

路は図A.2のようにそれぞれ3つの光の軌跡で構成されているとしよう。経路(1)は光の軌跡の空間ベクトル\(\overrightarrow{\mathrm{H_{1}}},\overrightarrow{\mathrm{H_{2}}},\overrightarrow{\mathrm{H_{3}}}\)で、経路(2)は\(\overrightarrow{\mathrm{G_{1}}},\overrightarrow{\mathrm{G_{2}}},\overrightarrow{\mathrm{G_{3}}}\)で構成されているとしよう。そして、それぞれ2番目の光の軌跡が経路に逆行しているとしよう。経路(1)の時間的距離は \[ |\overrightarrow{\mathrm{H_{1}}}|-|\overrightarrow{\mathrm{H_{2}}}|+|\overrightarrow{\mathrm{H_{3}}}| \] であり、経路(2)の時間的距離は \[ |\overrightarrow{\mathrm{G_{1}}}|-|\overrightarrow{\mathrm{G_{2}}}|+|\overrightarrow{\mathrm{G_{3}}}| \] である。この光の経路は始点と終点で、もう一方の経路と会合しており、光の経路の折れ点では、光の経路の定義より、会合している。よって、この2つの光の経路をぐるっと一周して1つの光の経路と考えると、全ての折れ点で会合していることになる。補題より、となり合う光の軌跡は会合という事実を崩さずに交換できるので、順次交換を繰り返せば、この光の経路は折れ点での会合という事実を崩さずに、各軌跡を並べ替えることができる。それで、経路(1)の逆行軌跡である\(\overrightarrow{\mathrm{H_{2}}}\)を経路(2)の方にもっていこう。\(\overrightarrow{\mathrm{H_{2}}}\)は経路(1)から見れば逆行しているが、経路(2)から見れば順行しているからである。同じ理由で経路(2)の逆行軌跡である\(\overrightarrow{\mathrm{G_{2}}}\)を経路(1)にもっていこう。すると光の軌跡は、図A.2のように\(\overrightarrow{\mathrm{H_{1}}},\overrightarrow{\mathrm{H_{3}}},\overrightarrow{\mathrm{G_{2}}}\)と\(\overrightarrow{\mathrm{Ｇ_{1}}},\overrightarrow{\mathrm{G_{3}}},\overrightarrow{\mathrm{H_{2}}}\)という順行のみから構成できる。この新しい2つの光の経路は終点で会合しているので、会合の原理(b)より距離は互いに等しくなければならない。すなわち \[ |\overrightarrow{\mathrm{H_{1}}}|+|\overrightarrow{\mathrm{H_{3}}}|+|\overrightarrow{\mathrm{G_{2}}}|= |\overrightarrow{\mathrm{G_{1}}}|+|\overrightarrow{\mathrm{G_{3}}}|+|\overrightarrow{\mathrm{H_{2}}}| \] でなければならない。ということは、実は元の2つの経路の時間的距離が等しかった、つまり \[ |\overrightarrow{\mathrm{H_{1}}}|-|\overrightarrow{\mathrm{H_{2}}}|+|\overrightarrow{\mathrm{H_{3}}}|= |\overrightarrow{\mathrm{G_{1}}}|-|\overrightarrow{\mathrm{G_{2}}}|+|\overrightarrow{\mathrm{G_{3}}}| \] であったということである。今の議論は、光の経路が3個の軌跡で構成されてなく、何個で構成されていても成り立つことである。よって、2つの事象を2つの光の経路で表わせるなら、その2つの光の経路の時間的距離は等しくなければならないという第2会合の原理(b)が証明されたことになる。会合の原理より、会合の原理(b)が証明されたので、今までの議論より、会合の原理(a)、(b)、第2会合の原理(a)、(b)という4つの原理すべてが同等であることが証明されたことになる(図A.3)。

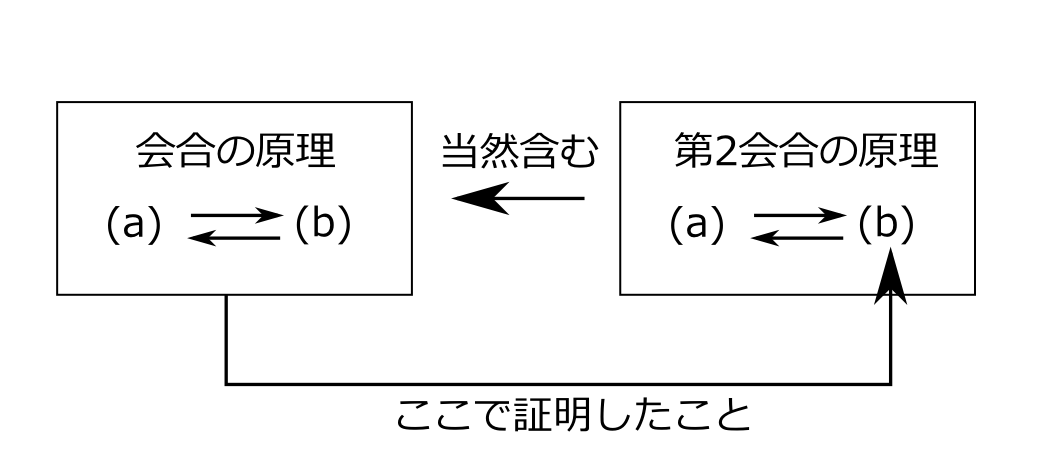
図A.3

A.2 ガリレオ変換により、会合の原理が満たされなくなってしまうこと

　この付録では、Ｓ系で会合の原理を満たしているとき、その軌跡をガリレオ変換でS'系に変換した場合、会合の原理を満たさないことを示す。座標系は第2.9節で設定したものを使う。S系において、X軸方向に光を発し、1mで反射して元の位置に戻る光の経路と、Y軸の正の向きに光を発し1m進んで反射し元の位置に戻る光の経路を考える(図A.4）。 この光の軌跡をS'系

図A.4

で考えよう。X'軸の正の向きに進む光の軌跡は \[ 1-v \] 負の方向に進む光の軌跡は \[ 1+v \] で計2mである。一方Y'軸の正の向きに進む光は \[ \sqrt{1+v^2} \] 負の向きに進む光も \[ \sqrt{1+v^2} \] 計\(2\sqrt{1+v^2}\)となり、2つの光の移動距離が異なってしまう。

目次

はしがき

第1章

第2章

付録A

あとがき

参考文献