光の軌跡の変換としてのローレンツ変換
2011年6月28日
第2章 光の軌跡の変換とローレンツ変換
2.1節 状況の設定
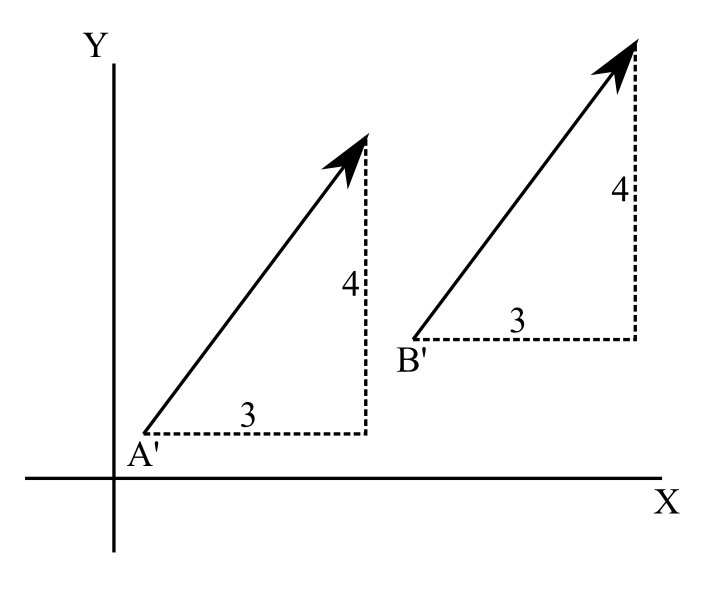
図2.1
ローレンツ変換を導出するにあたって状況を明確にしておこう。考察するのは2つの剛体が互いに一定の速さ\(v\)で動いている状況である。これは、一方の剛体(S系)から、もう一方の剛体(S'系)のどこかに目印をつけて、S系からその速度を測ると、S'系のどこに目印をつけ、又、いつ測ろうとも、同じ向きと同じ大きさをもつということである。例えばS系に図2.1のように直交座標\((x,y)\)を設けて、S'系の点A'の速度ベクトルを測ったら、\((3,4)\)であったなら、S’系の別の点B'の速度ベクトルも\((3,4)\)であるということである。又、立場を入れ替え、S’系からS系の任意の点の速度を測っても同じことが言えて、S系の点Cの速度がS'系から見て\((5,0)\)だったなら、S系の別の点Dの速度も\((5,0)\)となるということである。ここでS系から見たS'系の速度ベクトルの大きさ、すなわち速さと、S’系から見たS系の速さは等しいということを仮定しておこう。このことは、S系から見たS’系を見た速さより、S’系からS系を見た速さの方が、大きかったり小さくなったりする理由が見当たらないという互いの系の同等性から自明と考えていいと思う。今設定した状況では、空間のどの位置も同等であり、時間的にもいつも同等である。この空間・時間の一様性からローレンツ変換の線形性が出てくるわけである。
2.2節 軌跡の変換に帰着すること
ローレンツ変換とは、2つの事象の時間差、位置差が、2つの系でどう観測されるかという変換規則のことである。ところで第1.3節で述べたように、任意の2つの事象は光の軌跡をつなぎ合わせれば表わすことができるのであった。ということは光の軌跡の空間的変換の規則がわかれば、時間差、位置差の変換規則も求まるということである。例えば図2.2(a)のように、点
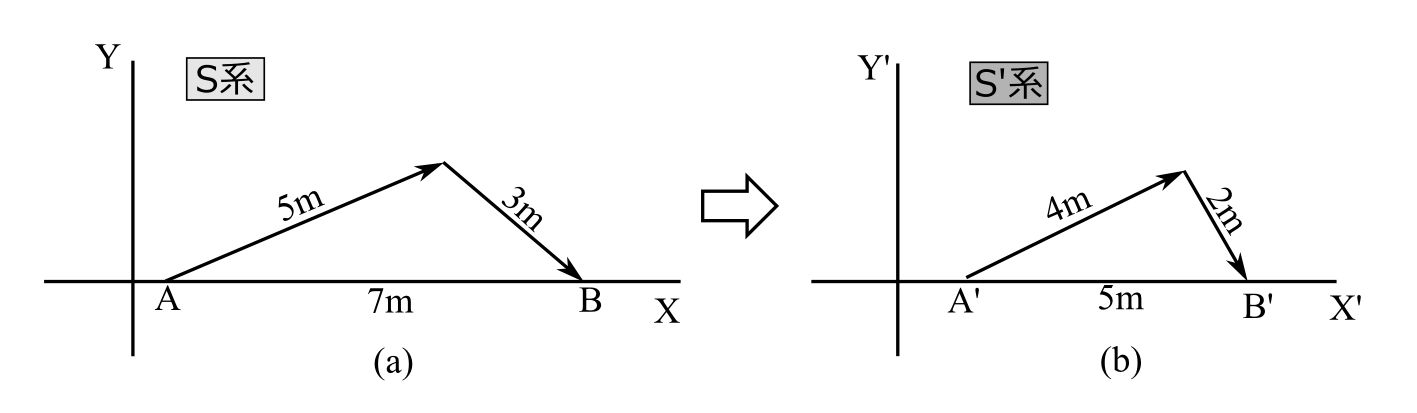
図2.2
A、点Bで起きた事象がある光の経路で表わせたとしよう。S系でのこの2つの事象の時間差は光の移動距離が\(5+3=8\)なので"8"、位置差は\(\overrightarrow{\mathrm{AB}}\)の空間ベクトルがX軸の方向に7m進んでいるので"7"、すなわち\((t,x)=(8,7)\)である。この光の軌跡をもう一方の系で観測すると図2.2(b)のように、光の移動距離が\(4+2=6\)で、空間ベクトル\(\overrightarrow{\mathrm{A'B'}}\)がX'軸の方向に5mだったとしよう。すると\((t',x')=(6,5)\)と求まる。すなわち、光の軌跡がどう変換されるかという知識から、2つの事象の時間差と位置差が、S系では(8,7)であるのが、S’系では(6,5)に変換されるということがわかるというわけである。まとめると
ローレンツ変換の導出は、光の軌跡が三次元空間的にどう変換されるかを求めることに帰着する
と言える。従って今後この空間的変換規則を求めていこう。
2.3節 光の軌跡の変換の線形性
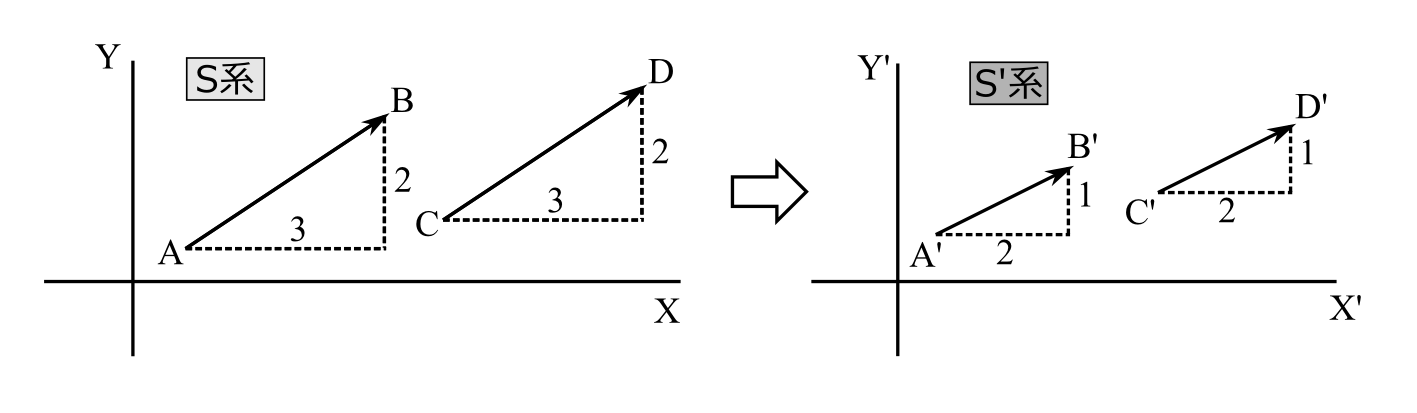
図2.3
今、図2.3のようにS系での光の軌跡\(\overrightarrow{\mathrm{AB}}\)があり、その成分が\((x,y)=(3,2)\)だったとしよう。そして、この光の軌跡をS’系で観測した\(\overrightarrow{\mathrm{A'B'}}\)の成分は\((2,1)\)だったとしよう。このとき、S系での別の光の軌跡\(\overrightarrow{\mathrm{CD}}\)の成分も\(\overrightarrow{\mathrm{AB}}\)と同じ\((3,2)\)ならば、それをS'系で観測すると、その成分は、当然\(\overrightarrow{\mathrm{A'B'}}\)と同じ\((2,1)\)となるはずである。空間時間に特別な点はなく一様である状況を設定したからである。すなわち
光の変換原理1 一方の系において、お互いに向きも長さもそれぞれ等しい2つの光の軌跡は、もう一方の系で測ってもお互いに向きも長さも等しくなる
と言える。このことから、光の軌跡の変換規則は、位置・時間を指定せずに求めればよいことになる。この原理からS系で光が例えば図2.4のように
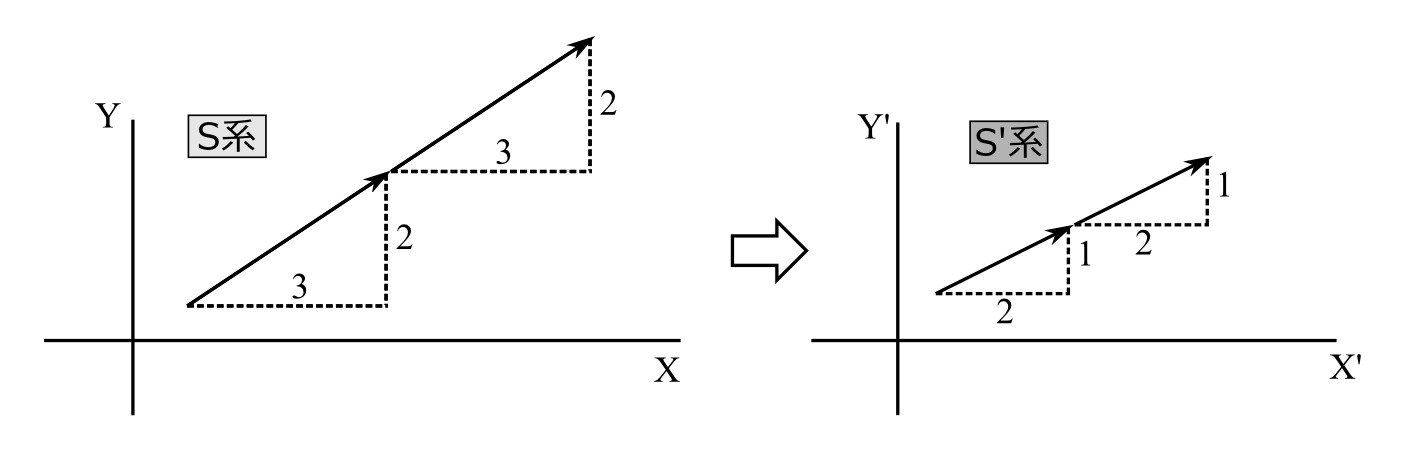
図2.4
\((3,2)\)進んで、さらにそのまま\((3,2)\)進むとすると、この光の軌跡は、\((3,2)\)が\((2,1)\)に変換されるとするならば、S’系では、\((2,1)\)進んでさらに\((2,1)\)進むことになる。つまり、S系で\(2(3,2)=(6,4)\)進む光は、S’系では、\(2(2,1)=(4,2)\)進むことになる。光の軌跡が2倍になれば、もう一方の系でも2倍になり、3倍になれば、もう一方の系でも3倍になる。逆に1/3倍になれば1/3倍になる。又、考えを組み合わせると、2/3倍になれば、2/3倍になると言える。以上より
命題2(光の軌跡の変換の線形性) ある系での光の軌跡\(\overrightarrow{\mathrm{AB}}\)が、もう一方の系で\(\overrightarrow{\mathrm{A'B'}}\)だったとすると、\(\overrightarrow{\mathrm{AB}}\)の\(\beta\)倍された光の軌跡\(\beta\overrightarrow{\mathrm{AB}}\)は、もう一方の系でも\(\beta\)倍され\(\beta\overrightarrow{\mathrm{A'B'}}\)となる。
と言える。
2.4節 運動方向の光の軌跡の変換

図2.5
S系の点OからS'系の運動方向に光を放射する。光は1m進んで点Pで反射し元の点Oに戻ってきたとしよう(図2.5)。 さて、この光の軌跡をS'系で考えよう。S系に対して速さ\(v\)で動いているS'系では光を放出した点をO'、反射した点をP'、光がS系の点Oに戻ってきた点をO''としよう。表にすると
\[ \begin{array}{ccc} \hline &\text{S系}&\text{S'系} \\ \hline 光の放出地点&\text{O}&\text{O'}\\ 光の反射地点&\text{P}&\text{P'}\\ 光の最終地点&\text{O}&\text{O''}\\ \hline \end{array} \]表2.1
表2.1のようになる。まず
光の変換原理2 S系で、S'系の運動方向に平行な光の軌跡は、S'系でも、その軌跡はS系の運動方向に平行である。
と言える。これは、お互いの運動方向に関して対称(注 運動方向に関してというべきか、直交方向に関してというべきか、言葉をどう使うべきかわからないが意味は分かってもらえると思う。)であるからである。S系では、光の軌跡が図2.6(a)のように相手の運動方向に平行であるのに、S'系では、光の軌跡が図2.6(b)の(I)のように相手の運動方向に平行でないなら、同じ

図2.6
理由で(II)という軌跡も考えられるからである。これはおかしいのでS'系でも相手の運動方向に平行になる。この光の変換原理2から、S'系では図2.7のように点O'、点P'、点O''がS系の運動方向に平行な1つの直線上に並ぶと言える。
S系でS'系の動いている方向に1m進んだ光は、S'系では未知数\(\alpha\)進んだとしよう。すなわちO'P'=\(\alpha\)とする。となると、S系で点Pで反射して、S'系の動いている向きと逆向きに1m進んだ光は、S'系では\(1/\alpha\)進むはずである。理由を述べよう。光が1m進んだというのが、その光の進行方向に動いている系で\(\alpha\)進んだと観測されるなら、2m進んだ光は、命題2(光の軌跡の変換の線形性)より、光の進行方向に動いている系では\(2\alpha\)進んだと観測されるはずである。すなわち、光の進行方向に動いている系では光の移動距離は\(\alpha\)倍される。一方反射した光は、立場が入れ替わり、S系が光の進行方向に動くわけだから、S系の光の移動距離はS'系のそれの\(\alpha\)倍である。今、S系で1mなので、S'系では\(1/\alpha\)になるというわけである。

図2.7
以上より、S'系では図2.7のように、光の放出点O'から反射点P'までの距離が\(\alpha\)、反射点P'から光の最終点O''までの距離が\(1/\alpha\)なので、光は合わせて\((\alpha+1/\alpha)\)進んだことになる。別の言い方をすれば点O'で光を放出してから、点O''に着くまでの時間が\((\alpha+1/\alpha)\)だということである。一方S系の光を放出した点OはS'系から見て速さ\(v\)で点O'から点O''に時間 \((\alpha+1/\alpha)\)かかって進んだのだから、進んだ距離O'O''=\(v(\alpha+1/\alpha)\)である。また光の移動距離の差よりO'O''=\((1/\alpha-\alpha)\) である。すなわち \[ \left(\alpha+\frac{1}{\alpha}\right)v=\frac{1}{\alpha}-\alpha \] でなければならない。これを未知数\(\alpha\)について解くと \begin{equation} \alpha=\sqrt{\frac{1-v}{1+v}} \label{a-kai} \end{equation} と求まる。以上より、
命題3(運動方向の変換規則)
(a) S系で、S'系の運動方向へ進行している光の軌跡は、S'系では、長さは\(\alpha=\sqrt{\frac{1-v}{1+v}}\)倍され、進行方向はS系の運動方向に対して反対向きとなる。
これを逆の立場から見ると
(b) S系で、S'系の運動方向に対して反対方向へ進行している光の軌跡は、S'系では、長さは\(\frac{1}{\alpha}=\sqrt{\frac{1+v}{1-v}}\)倍され、進行方向はS系の運動方向である。
と言える。この変換則は相手の系の速さが\(v\)であることを使って求めたのである。
2.5節 光のドップラー効果
ここで今の結論の応用例として光のドップラー効果について述べよう。この節の内容は論文の流れからはずれているので、飛ばしてもらっても後の理解に関係しない。今知りたいことは、ある光の波長を、ある系(S系)で観測したときの値と、S系からみてその光の進行方向に速さ\(v\)で動いている系でその光の波長を観測したときの値との関係である。まず議論の前提として光の波の山はどの系で見ても山であるということを仮定しておこう。これは決して自明なことではないが、電磁場の変換則から導けることである。水の波や、音の波なら、これは自明であろう。
今、波長が\(\lambda\)である光Gがあり、その山がある点Aに来たとしよう。それと同時に、その点Aから、光の進行方向と反対向きに波長測定用の光Hを発するとしよう。その光Hは、\(\lambda\)だけ進んだ点で、光Hを発したときに点Aにあった山の次の次の山と会合する。なぜなら、点Aで光を発したとき、次の次の山は\(2\lambda\)離れた点にあり、そしてお互い\(\lambda\)進んだ点で会合するからであ
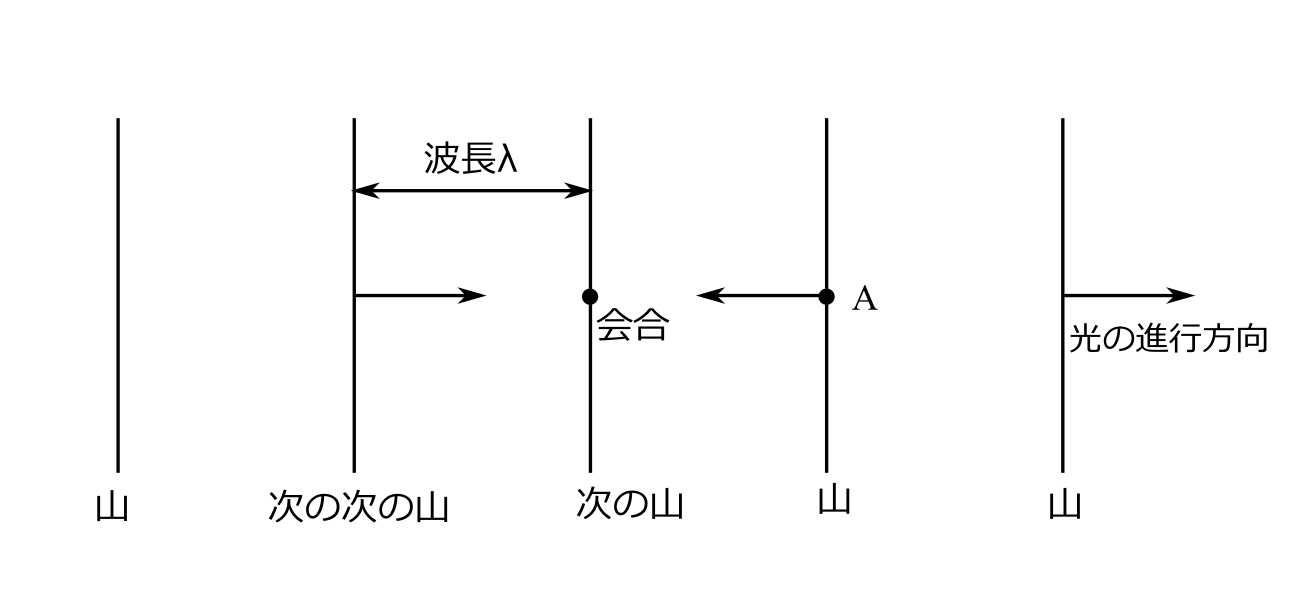
図2.8 点Aに山が来たとき光の進行方向の逆向きに光を発する。光は波長\(\lambda\)進んだとき次の次の山と会合する。
る。これは図2.8からも明らかであろう。すなわち、ある光Gの波長を知りたければ、ある点Aに光Gの山がきたとき、この点Aから、光Gの進行方向と逆向きに光Hを発し、その光Hが光Gの次の次の山とぶつかるまでに移動した距離を測ればよいということである。
点Aで、光Gの山が来たときに、波長測定用の光を発したという事実と、この測定用の光が次の次の山と会合したという事実は、どの系で見ても、そのことが起きているわけである。よって、別の系で、光Gの波長を知りたければ、測定用の光の移動距離がどう変換されるかを知ればよいわけである。となると、光の進行方向に動いている系というのは、測定用の光に対して逆向きに動いているわけだから、命題3(b)より、波長は\(1/\alpha\)倍され、光の進行方向と逆向きに動いている系というのは、測定用の光の向きに動いているわけだから、命題3(a)より、波長は\(\alpha\)倍される。以上より
命題4(ドップラー効果)
ある系で波長が観測された光を、
(a) その光の進行方向に速さ\(v\)で動いている系から観測すると波長は\(\sqrt{\frac{1+v}{1-v}}\)倍される。
又、同じ事だが、
(b) その光の進行方向に対して逆向きに速さ\(v\)で動いている系では波長は\(\sqrt{\frac{1-v}{1+v}}\)倍される。
と言える。
2.6節 運動方向に対して直交し同時である事象
S系で1m離れた点A、点Bで同時に起きた事象A(J)、B(J)を考える。直線ABはS'系の運動方向に対して直交しているとする(図2.9)。事象A(J)、B(J)をS'系で観測したときその位置をA'、B'とする。このとき直線A’B'はS系の運動方向に対して直交していると推測できる。理由を述べよう。S'系において直線A'B'とS系の運動方向とのなす角が図2.9(a)のように、もしA'の側の角度の方が小さいなら、同じ理由で図2.9(b)のように B'の側が小さいとも

図2.9
言えるわけである。これはおかしいので、直線A'B'は、S系の運動方向に直交していると言える。又、事象A(J)、B(J)はS'系で観測しても同時に起きたと推測できる。なぜなら、もしA(J)がB(J)より、先に起きたというなら、同じ理由でB(J)の方がA(J)より先に起きたと主張できるからである。最後に、直線A'B'の長さは1mであると推測できる。理由を述べよう。もし、S系の1mの距離がS'系で1mと異なり、例えば3mだったとしたら、時間空間の一様性よりS系での1/3mがS'系で1mと観測されるはずである。一方の系の1mが3mに変換されるのに、もう一方の系の1mが1/3mに変換されるのは互いの系が同等であると設定したことに反する。よって、A'B'の長さは1mのはずである。以上の議論より
命題5 S系で同時に起きた2つの事象の位置を結んだ線がS'系の運動方向に直交しているなら、S'系でも、その2つの事象は同時に起き、かつ2つの事象が起きた点を結んだ線はS系の運動方向に直交し、又、その距離もS系で測った距離と等しい。
と言える。
これで十分説得力のある推論を行ったわけだが、本来同時ということは光の軌跡で表わさなければならない。それが、この論文の本旨である。それで、今の命題5を光の軌跡の変換で説明してみよう。S系で図2.10のよう

図2.10
に、光を点OからS'系の運動方向と直角方向に、同時に互いに180度反対の向きに放出し、それぞれ1m進んで、点A、点Bに到達したとしよう。その事象をそれぞれA(J)、B(J)と呼ぼう。明らかに、S系ではA(J)とB(J)は同時である。S'系では光を放出した点をO'、事象A(J)、B(J)に対応する点をA'、B'としよう。このとき平面O'A'B'はS系の運動方向と平行になると推測できる。なぜなら、図2.10のように平面O'A'B'がS系の運動方向に平行でないのは、相手の運動方向に関して対称であることに反するからである。このことを枠にくくって書いておこう。
光の変換原理3 S系において、ある点からS'系の運動方向と直角方向に同時に互いに180度反対向きに光を放出したとすると、S'系では、この2つの光の軌跡によってできる平面はS系の運動方向に平行である。
ところで、
設定 相手の系の運動方向に対して直角に1m進む光は、もう一方の系では、相手の運動方向に\(\beta\)、直角方向に\(\gamma\)進む
としよう。するとS'系では光の軌跡は図2.11(a)のようにS系の運動方向に関して対称になるであろう。A'O'とB'O'の距離が等しいので、S'系でも事象A(J)、B(J)は同時である。又、直線A'B'はS系の運動方向に直交している。次に図2.11(b)のように、点A'に着いた光は、方向を変え点B'の方向に進み、点B'に着いた光は点A'の方向に進むとする。光は会合の原理より、それ

図2.11

図2.12
ぞれ\(\gamma\)進んだ点で会合する。この一連の光の軌跡をS系で観測するとどうなるか。今度はS系とS'系の立場が入れ替わったわけで、S'系でS系の運動方向に対して直角に\(\gamma\)進む光は、S系では上記設定と命題2(光の軌跡の変換の線形性)より、図2.12のようにS'系の運動方向に\(\gamma\cdot\beta\)、直角方向に\(\gamma\cdot\gamma\)進むことになる。 すなわちAOの長さは\(\gamma^2\)である。一方、最初の設定より、AO=1なので、結局\(\gamma=1\)でなければならない。よってA'B'の長さはS系での長さと同様2mでなければならない。これで最初に光を使わないで述べた命題5に光の軌跡の変換による説明がついたわけである。
以上の結論から直交平面上の合同性も言える。今、S系でS'系の運動方向に対して直交する面上の3点A,B,Cで同時に起きた事象を考えよう。S'系ではこの事象の起きた点をそれぞれA',B',C'としよう。このとき、S系では点A、点Bで起きた事象は同時であり、直線ABは相手の運動方向に直交しているので、命題5よりAB=A'B'となる。同様にBC=B'C'、CA=C'A'となる。対応する三辺が等しいので三角形ABCと三角形A'B'C'は合同である(図2.13)。ということは任意の多角形も合同になるということである。以上より
命題6(直交面上の合同性) あるいくつかの事象が、S系では、S'系の運動方向に直交する面上で同時に起きたとし、その起きた点によってできる多角形をAとしよう。このとき、S'系では、この事象はS系の運動方向に直交する面上で同時に起き、その起きた点によってできる多角形A'は多角形Aと合同である。
と言える。
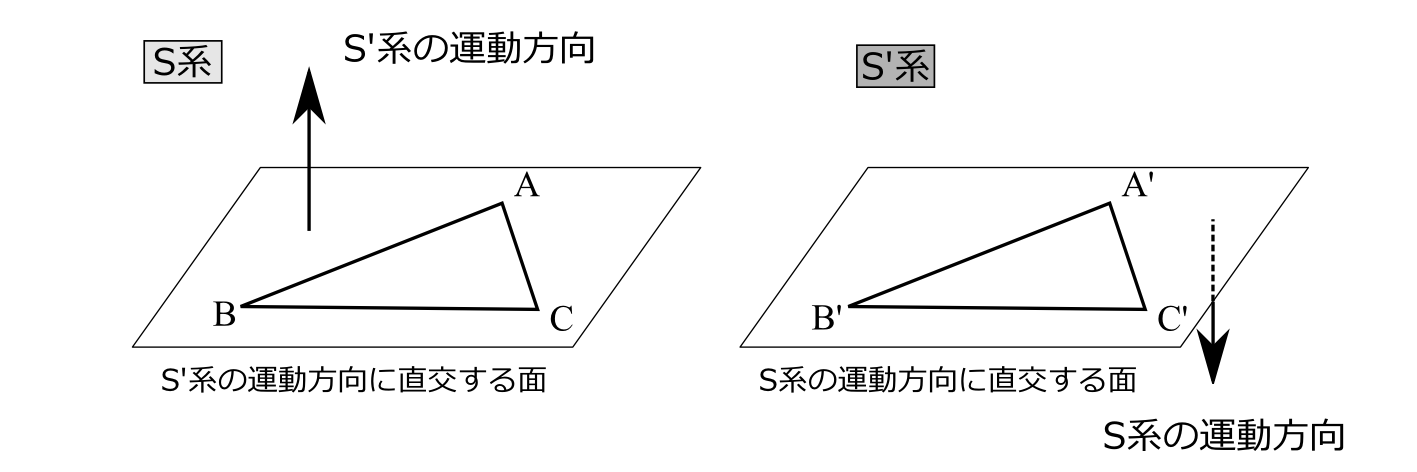
図2.13
2.7節 運動方向と異なる向きの光の軌跡の変換
次に今までの結果を利用して、相手の系の運動方向と異なる向きの光の軌跡が、どう変換されるかを考えよう。今、S系において図2.14(a)のように、長さ\(a\)、S'系の運動方向に成分\(b\)、直角方向に成分\(c\)をもつ光の軌跡OA
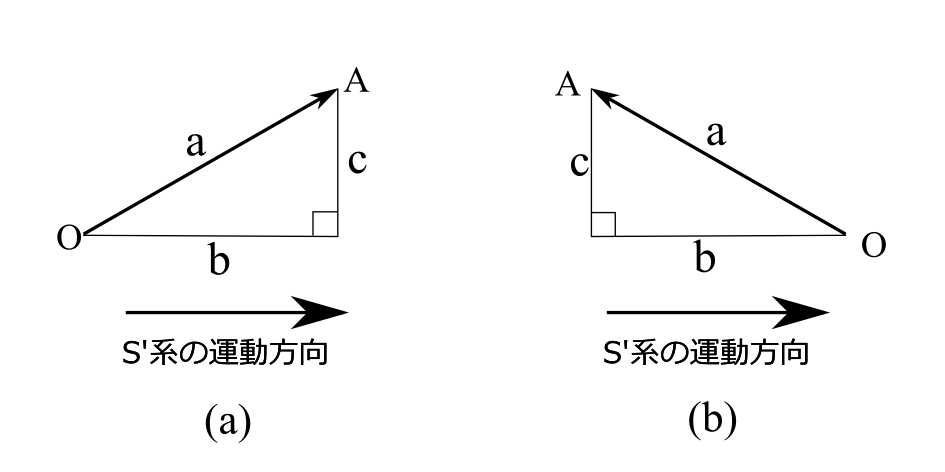
図2.14
を考える。ここで\(b\)は負の場合も想定しよう。\(b\)が負の場合は図2.14(b)のようにS'系の運動方向と逆向きの成分をもつとする。この光の軌跡はS'系では長さ\(a'\)、S系の運動方向に反対向きに成分\(b'\)、直角方向に成分\(c'\)をもつ光の軌跡に変換されるとしよう。我々は\(a,b,c\)を使って\(a',b',c'\)の値を表したいのである。
さて、この光の軌跡OAをすでに変換規則がわかっている光の経路で表わしてみよう。図2.15(a)のように点Oから点Aに光が発せられると同時に点OからS'系の運動方向に光を発する。その光はS'系の運動方向に\(R\)進み、点Pで反射して反対方向に\(L\)進み、点Bに着くとする。\(R\)と\(L\)は \begin{equation} R+L=a,\quad R-L=b \label{RL} \end{equation} を満たしているとする。 つまり、光が点Bに着いたとき点Oからの光が点A
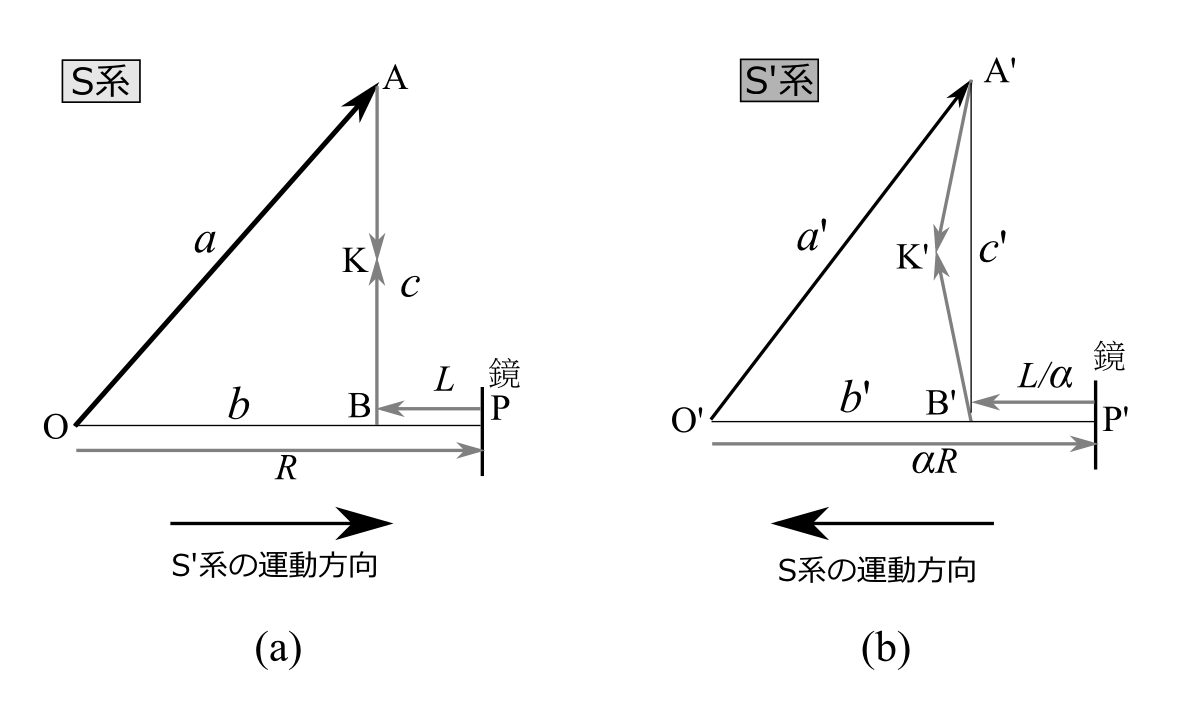
図2.15
に着いたときと同時になるようにし、 直線ABとOBが直交するように\(R\)と\(L\)を決めるのである。点A、点Bの間は、ABの中点Kに点A、点Bから光が向かっているとする。光の経路O\(\rightarrow \)P\(\rightarrow \)B\(\rightarrow\)K\(\rightarrow\)Aと光の経路O\(\rightarrow\)Aは時間的距離が等しいので点Aで会合する。よって、光の経路O\(\rightarrow\)P\(\rightarrow\)B\( \rightarrow\)K\(\rightarrow\)Aが、いかに変換されるかがわかればOAの変換がわかるということである。ここで、あいまいさを防ぐために記号を表に整理しておこう。
\[ \begin{array}{cccc} \hline 事象&その内容& \text{S系}& \text{S'系} \\ \hline \text{O(J)}&\text{点Oから点A、点Pに向かって光が発せられた事象}&\text{O}&\text{O'}\\ \text{A(J)}&\text{点Oからの光が点Aに着いた事象}&\text{A}&\text{A'}\\ \text{P(J)}&\text{点Oからの光が点Pに着いた事象}&\text{P}&\text{P'}\\ \text{B(J)}&\text{点Pからの光が点Bに着いた事象}&\text{B}&\text{B'}\\ \text{K(J)}&\text{点Aからの光と点Bからの光が会合した事象}&\text{K}&\text{K'}\\ \hline \end{array} \]この光の経路は図2.15(b)のように、S'系では命題3(a)より、S系の運動方向と逆向きに\(\alpha R\)、命題3(b)より、進行方向に\(L/\alpha\)進んで点B'に着く。 事象A(J)とB(J)はS系では同時であり、直線ABはS'系の運動方向に直交しているので、S'系でも直線A'B'は 命題5より、S系の運動方向に直交し、長さはA'B'=ABである。よって、\(c'=c\)である。又、直線A'B'がS系の運動方向と直交しているので、\(b'=\)O'B'\(=\alpha R-L/\alpha\)である。光の経路O'\(\rightarrow \)A'\(\rightarrow \)K'とO'\(\rightarrow \)P'\(\rightarrow \)B'\(\rightarrow \)K'は点K'で会合しているので、会合の原理より \[ \text{O'A'+A'K'=O'P'+P'B'+B'K'} \] でなけれならない。そしてA'K'=B'K'なので \[ \text{O'A'=O'P'+P'B'} \] を満たす必要がある。O'P'+P'B'\(=\alpha R+L/\alpha\)なので、\(a'=\)O'A'\(=\alpha R+L/\alpha\)でなければならない。以上のことをまとめると
命題7(運動方向と異なる向きの光の変換規則) S系において、長さ\(a\)、S'系の運動方向に成分\(b\)、直角方向に成分\(c\)をもつ光の軌跡はS'系では、長さ\(a'=\alpha R+L/\alpha\)、S系の運動方向に反対向きの成分\(b'=\alpha R-L/\alpha\)、直角方向に成分\(c'=c\)の軌跡に変換される。略式で書くと \[ (a,b,c)\longrightarrow (\alpha R+L/\alpha\, ,\, \alpha R-L/\alpha\, ,\, c) \] である。ここで\(R=(a+b)/2\,,\, L=(a-b)/2\)であり、\(\alpha=\sqrt{\frac{1-v}{1+v}}\)である。\(b\)は負の場合もあるとする。
この命題は\(c=0\)とおけば、命題3を含んでいることになる。
ところで、\(a'\)の値は今、会合の原理を使って
\[
a'(\text{会})\equiv \alpha R+L/\alpha
\]
と求めたが、三平方の定理からも
\begin{equation}
a'(\text{三})\equiv \sqrt{b'^2+c'^2}
\label{teigisan}
\end{equation}
と求まる。そこで、この2つの方法で求めた値が等しいことを確認する必要がある。
【証明】
\(c'^2=c^2\)であり、S系での三平方の定理より\(c^2=a^2-b^2\)である。これに式\ref{RL}の\(R\)と\(L\)を代入すると
\begin{align*}
c'^2=&a^2-b^2\\
=&(R+L)^2-(R-L)^2\\
=&4RL
\end{align*}
である。これを式\ref{teigisan}に代入すると
\begin{align*}
a'(\text{三})=&\sqrt{\left(\alpha R-L/\alpha \right)^2+4RL}\\
=&\sqrt{\left(\alpha R+L/\alpha \right)^2}\\
=&aR+L/\alpha\\
\end{align*}
である。よって\(a'\)の値は、会合の原理から求めた値と三平方の定理から求めた値と一致することが確認できた。【証明終】
同じことなのだが理解を深めるために別証を書いておこう
【別証】
\begin{align*}
a'^2(\text{会})-b'^2=&(\alpha R+L/\alpha)^2-(\alpha R-L/\alpha)^2\\
=&4RL\\
=&a^2-b^2
\end{align*}
となり、会合の原理を満たしていれば、三平方の定理に関係なく
\begin{equation}
a'^2(\text{会})-b'^2=a^2-b^2
\label{kankeinaku}
\end{equation}
が成り立つ。S系での三平方の定理より\(a^2-b^2=c^2\)なので
\[
a'^2(\text{会})-b'^2=c^2
\Longleftrightarrow
a'(\text{会})^2=b'^2+c'^2
\Longleftrightarrow
a'(\text{会})^2=a'(\text{三})^2
\]
となり、両者が一致することがわかる。
【別証終】
しかし、会合の原理から求めた値と三平方の定理から求めた値とが一致するというのは私には大きな驚きである。今までの議論からわかるように、\(a'(\text{会})\)の求め方は相手の系の速さが\(v\)であることや、対称性を用いて求めたものであり、三平方の定理とは一切関係ない。それなのに、両者が一致するというのは私には不思議でしょうがない。もちろん、この不思議と感じるのは、こうあらねばならないという誤った決めつけがあるか、理解不足が原因なのだろう。想像の域を出ないが、おそらく、三平方の定理は平行線の公理より、導き出されたものであり、平行線の公理は空間が一様であることに関係ある。一方、この論文での光の軌跡の変換方法も、空間の一様性を使って導出している。そういうことで関係があるのだろう。
2.8節 会合の原理から三平方の定理の導出
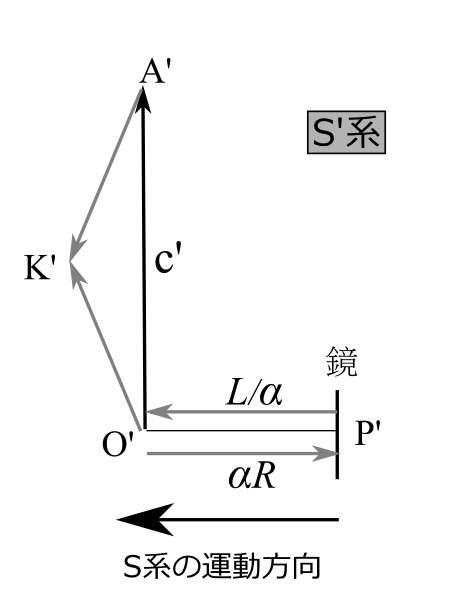
図2.16
ところで、三平方の定理と会合の原理が矛盾しないということは、2つの系で会合の原理が成り立つためには三平方の定理が成り立たなければならないというこが言えそうである。すなわち、2つの系で会合の原理が成り立つことから三平方の定理を証明できるということを示唆していると考えられる。実際、そのとおりであり、以下に証明を述べる。この証明は今後の理解に関係ないので飛ばしてもらって差し支えない。
【証明】
前節式\ref{kankeinaku}で述べたように三平方の定理が成り立つということとは関係なく、会合の原理が成り立つなら
\[
a'^2(\text{会})-b'^2=a^2-b^2
\]
が成り立つ。ここで\(b'=0\)となるようにS'系の速さ\(v\)を決めれば、S'系では三角形がつぶれて\(a'(\text{会})=c'\)となる。\(c'=c\)なので結局
\[
c^2=a^2-b^2
\]
が成り立つというわけである。【証明終】
【別証】この証明では少し簡潔すぎるので、\(b'=0\)となるような光の経路を実際に考えて三平方の定理を証明してみよう。
記号は前節と同じとする。今は\(b>0\)としておこう。今、S'系の速さを十分速くとり、S系において点Oから出た光が点Pで反射して点Bに着いたとき(これは点Oからの光が点Aに着いたときと同時)、S'系の点O'が点Bに着くようにする。すなわちS'系では、図2.16のように、点P'で反射した光が点O'に戻ってき、そしてO'A'がS系の運動方向に直交するように速さをとるのである。
このような速さをとることは当然可能で、\(v=b/a\)とすればよい。\(a>b\)なので\(v<1\)となる。実際S'系において、点P'で反射した光が点O'に戻ってくるという条件は\(\alpha R=L/\alpha\)ということであり、これを変形すると
\[
\alpha R=\frac{L}{\alpha} \Longleftrightarrow \alpha^2=\frac{L}{R}\Longleftrightarrow \frac{1-v}{1+v}=\frac{a-b}{a+b}\Longleftrightarrow \frac{1-v}{1+v}=\frac{1-b/a}{1+b/a}
\]
となり、\(v=b/a\)であれば確かによい。光は点K'で会合するので
\[
\text{O'A'=2O'P'}
\]
が成り立つはずである。O'A'=\(c'\)=\(c\)なので、(2O'P')\(^2\)=\(a^2-b^2\)であることを示せればよい。実際、
\[
(2\text{O'P'})^2=(2\alpha R)^2=4\alpha^2R^2
\]
であり、今の場合\(\alpha R=L/\alpha\)なので\(4\alpha^2 R^2=4RL\)。そして
\[
4RL=4\cdot \frac{a+b}{2}\cdot \frac{a-b}{2}=a^2-b^2
\]
となり、よって(2O'P')\(^2\)=\(a^2-b^2\)となる。すなわち\(a^2=b^2+c^2\)となる。【別証終】
以上より
命題8 2つの系で会合の原理が成り立つためには、三平方の定理が成り立たなければならない
ということが証明された。おそらく、三平方の定理が成り立つことと、平行線の公理は同等であると思う。平行線の公理より三平方の定理の証明は、ユーグリッドの原論や普通の幾何学の本に出ているが、おそらく三平方の定理から平行線の公理を導けるであろう。このことは数学の世界では既に証明されているのではないだろうか。そう仮定すると上記命題は
予想 2つの系で会合の原理が成り立つためには、平行線の公理が成り立たなければならない。
と言い換えられる。こう述べると不思議さはあまり感じなくなる。平行線の公理が成り立たないようでは、空間が等方的でなく、会合の原理が成り立ちそうもないからである。
2.9節 任意の方向の光の軌跡の変換規則
2.9.1 空間座標の設定
任意の光の軌跡の変換則を述べるためにS系、S'系に3次元空間座標系を設定しよう。S系において、S'系の運動方向に直交する平面を考え、その平面内で同時に起きる3つの事象O(J)、A(J)、B(J)を考える。その事象の位置を点O、点A、点Bとする。直線OAと直線OBは直交しているとする。点OからS'系の運動方向へX軸をとる。又、点Oから点Aに向かってY軸、点Oから
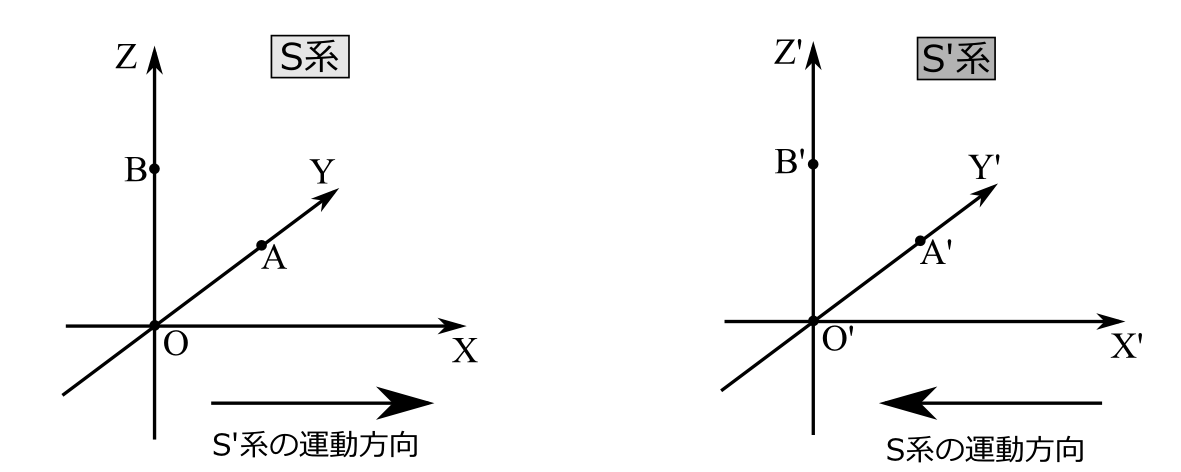
図2.17
点Bに向かってZ軸をとる(図2.17)。S'系ではO(J)、A(J)、B(J)が起きた場所の点をO'、A'、B'とする。点O'からS系の運動方向と反対向きにX'軸をとる。点O'から点A'に向けてY'軸を取る。点O'から点B'に向けてZ'軸を取る(図2.17)。前節の命題6(直交面上の合同性)よりY'軸とZ'軸は直交する。
2.9.2 この空間座標での有用な命題
この空間座標の設定から言えることを述べよう
命題9 S系において、事象A(J)、B(J)が起きた点をA、Bとし、直線ABがX軸に平行なら、S'系においても事象A(J)、B(J)に対応する直線A'B'はX'軸に平行である。
【証明】 1.3節の命題1で述べたように、ある系における2つの事象差は、その2つの事象が起きた点を結んだ直線上の光の経路で表わすことができる。S系において直線ABはX軸に平行なので、この光の経路はX軸に平行である。ということは光の変換原理2で述べたように、この光はS'系においてはX'軸に平行である。よって直線A'B'はX'軸に平行である。【証明終】
命題10 どんな事象でも、その事象のS系での位置の\(y\)座標、\(z\)座標とその事象のS'系での位置の\(y'\)座標、\(z'\)座標はそれぞれ等しい。
【証明】
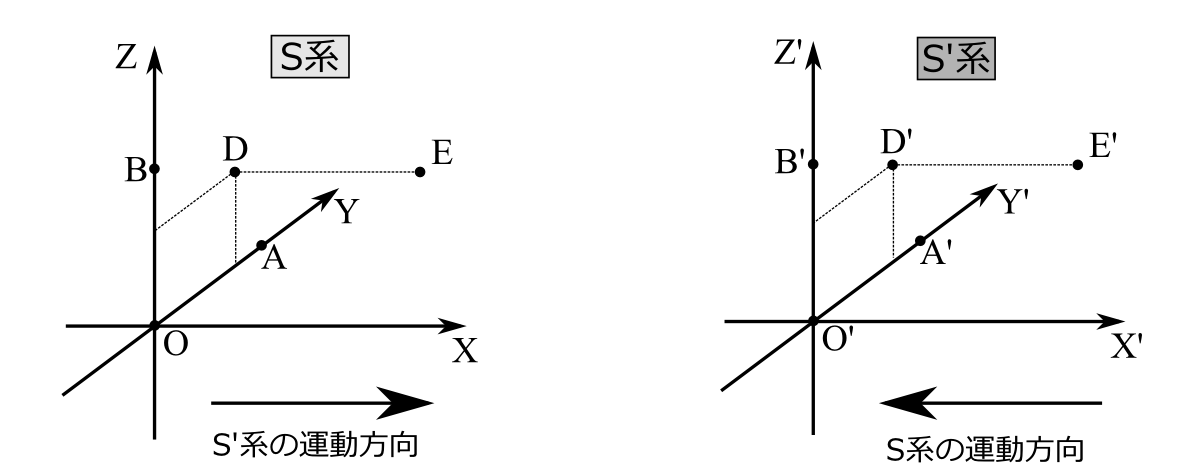
図2.18
S系において、この事象E(J)が起きた点をEとする。点EからYZ平面に垂線をおろした点をDとする(図2.18)。点Dにおいて、座標系を設定したときの事象O(J)と同時に起きた事象をD(J)としよう。D(J)のS'系での位置D'も命題6よりY'Z'平面に上にあり、かつ、\(y'\)座標、\(z'\)座標は、S系のそれに等しい。直線DEはS系においてX軸に平行なので、直線D'E'も命題9より、X’軸に平行である。よって点E'の\(y'\),\(z'\)座標は点D'のそれと等しい。よって点E'、点Eの\(y\)座標\(z\)座標はそれぞれ等しい。【証明終】
命題7と命題10より、今設定した座標系では光の軌跡の変換について以下のことが言える
命題11(任意の方向の光の軌跡の変換規則) 長さ\(a\)、\(x,y,z\)成分が\(b,c,d\)である光の軌跡はS'系では \[ (\alpha R+L/\alpha\, ,\, \alpha R-L/\alpha\, ,\, c\,,\,d) \] に変換される。ここで順番は、長さ、\(x',y',z'\)成分である。又、\(R=(a+b)/2,\quad L=(a-b)/2\)であり又\(\alpha=\sqrt{(1-v)/(1+v)}\)である。\(a>0\,,\,b,c,d\)は任意とする。\(R,L,\alpha\)を消去すれば \[ \left(\frac{1}{\sqrt{1-v^2}}\,a+\frac{-v}{\sqrt{1-v^2}}\,b\, ,\quad \frac{-v}{\sqrt{1-v^2}}\,a+\frac{1}{\sqrt{1-v^2}}\,b\, ,\quad c\,,\quad d\right) \] となる。
これで光の軌跡の変換則が完全にわかったわけである。第2.2節で述べたようにローレンツ変換は、光の軌跡の変換則を求めることに帰着する。つまり、任意の2つの事象の事象差の変換規則は、光の軌跡をつなぎ合わせた光の経路の変換を求めれば求まるわけである。
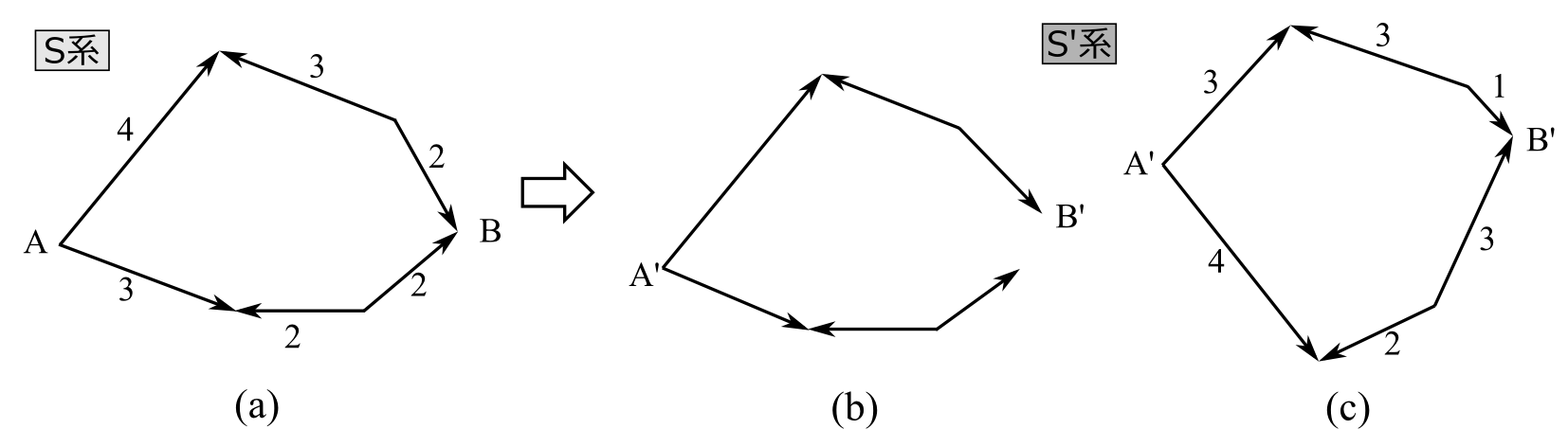
図2.19
2.9.3 矛盾がないこと
ところで、上記命題11で述べられた変換規則が第2会合の原理などに矛盾しないかを確かめる必要がある。つまり、2つの事象を2つの光の経路で表わしたとき、第2会合の原理で述べたように、この2つの経路の時間的距離が等しく、当然空間ベクトルも等しいわけであるが、これを上記命題11の方法で経路中の軌跡を変換したとき、この2つの光の時間的距離、空間ベクトルが、それぞれ等しくなるかということを確認する必要がある。これは、S系において図2.19(a)のように、点A、点Bで起きた事象を2つの経路で表わしたとき、それぞれの光の経路を命題11の方法でS'系に変換し、始点を合わせた場合、終点の位置が図2.19(b)のように異なってしまわないか。又、終点は一致するが、それぞれの経路の時間的距離が図2.19(c)のように異なってしまわないかということを確認したいわけである。つまり確認したいことは
確認すべきこと S系における2つの経路の時間的距離と空間ベクトルがそれぞれ互いに等しいなら、命題11の変換規則で変換したとき、S'系でも時間的距離と空間ベクトルがそれぞれ等しくなる。
ということである。それでは確認しよう。
空間ベクトルの\(y\)成分については、変換によって値が変化しない。そして、S系での2つの光の経路で空間ベクトルの\(y\)成分の変化量は等しい。よって、変換後の2つの経路の\(y'\)成分の変化量も互いに等しい。\(z\)成分も同様である。次に時間成分と\(x\)成分について考える。そのために、ある1つの光の経路 A\(\rightarrow\)Bが命題11の規則で、どう変換されるかを考えよう。簡単のた

図2.20
め、その経路A\(\rightarrow\)Bは、図2.20のように、3つの直線で構成されているとしよう。そして、各光の軌跡は経路の向きと(1)同じ(2)逆(3)同じであり、(長さ、\(x\)成分)がそれぞれ、 \[ (a_1,b_1)\quad(a_2,b_2)\quad(a_3,b_3)\quad a_i>0 \] だったとしよう。この経路の時間的距離は定義より\(a_1-a_2+a_3\)、空間ベクトルの\(x\)成分は\(b_1-b_2+b_3\)である。2番目の軌跡の向きは逆行しているので符号をマイナスにしなければならないことに注意しよう。さて、これをS'系に変換すると、各軌跡は命題11より、 \[ a'_i=Aa_i+Bb_i \quad b'_i=Ba_i+Ab_i \quad(i=1,2,3) \] と変換される。ここで\(A=1/\sqrt{1-v^2},\quad B=-v/\sqrt{1-v^2}\)と置いた。S'系でのこの光の経路の時間的距離と空間ベクトルの\(x'\)成分は、2番目の軌跡は逆行していることに注意すると、 \begin{equation} \begin{split} a_1'-a_2'+a_3'=A(a_1-a_2+a_3)+B(b_1-b_2+b_3)\\ b_1'-b_2'+b_3'=B(a_1-a_2+a_3)+A(b_1-b_2+b_3) \end{split} \label{ab} \end{equation} となる。このように光の経路のS'系における時間的距離、空間ベクトルの\(x'\)成分ともに、S系における時間的距離と\(x\)成分の値だけで完全に決まる。今の場合、光の経路は3つの軌跡で構成されていたが、このことは何個の軌跡で構成されていても成り立つことは明らかであろう。S系での2つの経路は、時間的距離も、空間ベクトルの\(x\)成分も互いに等しい。ゆえに、それを変換したS'系における時間的距離と空間ベクトルの\(x'\)成分はそれぞれ等しくなる。以上より
命題12 S系における2つの光の経路を命題11の方法でS'系に変換した場合、S系で2つの経路の時間的距離と空間的ベクトルがそれぞれ互いに等しければ、S'系でも時間的距離と空間的ベクトルがそれぞれ互いに等しくなる。
と言える。
さて、式\ref{ab}において\(a_1-a_2+a_3\)、\(a_1'-a_2'+a_3'\)は各系における2つの事象の時間差\(\Delta t, \Delta t'\)、\(b_1-b_2+b_3\)、\(b_1'-b_2'+b_3'\)は各系における\(x\)成分\(\Delta x, \Delta x'\)であった。今の場合は光の経路が3つの軌跡から構成されていたが、これが何個で構成されていようと式\ref{ab}は成り立つ。そして任意の2つの事象は、光の経路で表わすことができ、今確認したように、変換は一意であった。従って、任意の2つの事象の変換則について以下のことが言える。
命題13(ローレンツ変換) S系において任意の2つの事象の時間差、空間ベクトルの差が\((\Delta t,\Delta x, \Delta y ,\Delta z)\)のときS'系では
\[ \Delta t'= \frac{1}{\sqrt{1-v^2}}\Delta t+\frac{-v}{\sqrt{1-v^2}}\Delta x\qquad \Delta x'= \frac{-v}{\sqrt{1-v^2}}\Delta t+\frac{1}{\sqrt{1-v^2}}\Delta x\qquad \Delta y'=\Delta y\qquad \Delta z' =\Delta z \]
と変換される。座標系はこの節の最初に設定したものである。
以上で完全にローレンツ変換が求まったわけである。