第10章　電磁場と荷電粒子の解析力学

この章の目的はローレンツ力の式とマクスウェル方程式を正準方程式の形で書くことである。それは量子電磁気学のためである。粒子の量子力学の構成法というものを振り返ってみれば、古典力学のハミルトニアンの正準変数\(p,q\)から\([{\hat{q},\hat{p}}]=i\hbar\)という交換関係を設定することが始まりであった。同じことを量子電磁気学でもしたいわけである。電磁場でも\(p,q\)に対応するものをみつけ\([{\hat{q},\hat{p}}]=i\hbar\)としたいわけである。。

さて、粒子の力学ではハミルトニアンはラグランジアンをルジャンドル変換して導いた。それで電磁場と荷電粒子の場合も、ラグランジアンとラグランジュ方程式を作り、それからハミルトニアンと正準方程式を作ることにする。ラグランジュ方程式はローレンツ力の式とマクスウェル方程式を表すようにする。そうすれば自動的に正準方程式もそれらを表すことになる。考え方はこれにつきている。後は式変形をするだけである。 記号は非常にややこしく、計算は繁雑を極めているが、していることは単純作業である。

10-1節　ラグランジアン

まず簡単に古典電磁気学を復習しよう。マクスウェル方程式は \begin{equation} \nabla\cdot \mathbf{B}=0 \label{d1} \end{equation} \begin{equation} \nabla\times \mathbf{E}=-\frac{1}{c}\frac{\partial\, \mathbf{B}}{\partial\, t} \label{d2} \end{equation} \begin{equation} \nabla\cdot\mathbf{E}=4\pi k\rho \label{d3} \end{equation} \begin{equation} \nabla\times \mathbf{B}=\frac{4\pi k}{c}\mathbf{J}+\frac{1}{c}\frac{\partial\, \mathbf{E}}{\partial\, t} \label{d4} \end{equation} であり、ローレンツ力の式は \begin{equation} m\ddot{\mathbf{X}}=q\mathbf{E}+q\;\frac{\mathbf{\dot{X}}}{c}\times \mathbf{B} \label{d5} \end{equation} であった。ポテンシャルとして\(\phi,\mathbf{A}\)を導入して \[ \mathbf{E}=-\nabla \phi-\frac{1}{c}\frac{\partial\, \mathbf{A}}{\partial\, t} \qquad\qquad \mathbf{B}=\nabla\times \mathbf{A} \] と表せばマクスウェル方程式(\ref{d1})(\ref{d2})は自動的に満たされるのであった。単位系だが、cgs単位系なら\(k=1\)とし、SI単位系なら\(k=\frac{1}{4\pi \epsilon_0}\)とし、さらに\(\mathbf{B}\to c\mathbf{B}\)、\(\mathbf{A}\to c\mathbf{A}\)と置き換えればよい。

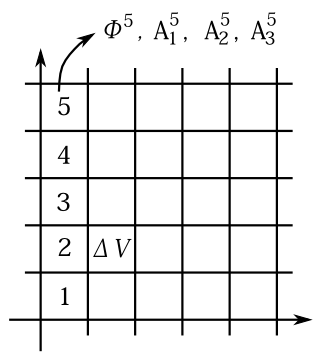
図10-1　 空間を細かい立方体に分割し、その各微小部分での\(\phi\),\(\mathbf{A}\)を力学変数とする。

さて、粒子の力学では、力学変数\(q\)は個々の粒子の位置座標\(X_i\)であった。一方、電磁場の場合、力学変数\(q\)に対応するのはポテンシャルの\(\phi(\mathbf{r}),\mathbf{A}(\mathbf{r})\)なのだが、それは次のような意味である。 空間を立方体の微小体積\(\Delta V\)ごとに十分細かく分割し、その１つ１つの体積領域に番号をふる(図10-1)。そして番号\(\beta\)の領域の位置でのポテンシャルを\(\phi^\beta,A_1^\beta,A_2^\beta,A_3^\beta\)と書き、これを力学変数とする。だから、今着目している系を100分割したとしたら、力学変数は400個できるわけである。粒子の力学変数\(X_i\)の指標\(i\)に対応するものが\(\phi^\beta\)の\(\beta\)であり、\(A_i^\beta\)の\(i\)と\(\beta\)である。ここで\(A_i\)の\(i\)は\(x,y,z\)の\(1,2,3\)である。粒子にも番号をふる。\(\lambda\)番目の粒子の位置座標を \(\mathbf{X}^\lambda=(X_1^\lambda,X_2^\lambda,X_3^\lambda)\)、電荷を\(q^\lambda\)、質量を\(m^\lambda\)と書こう。 この力学変数を使って天下り的にラグランジアンを書き下そう。

電荷と電磁場のラグランジアン \[ L= \sum_{\lambda,i}\frac{1}{2}m^\lambda (\dot{X}_i^\lambda)^2- \sum_\lambda q^\lambda\phi(\mathbf{X}^\lambda)+ \sum_{\lambda,i}\frac{q^\lambda}{c}\dot{X}_i^\lambda A_i(\mathbf{X}^\lambda)+ \frac{\Delta V}{8\pi k}\sum_\beta\left(\left|\mathbf{E}^\beta\right|^2-\left|\mathbf{B}^\beta\right|^2\right) \]

ここで\(\phi(\mathbf{X}^\lambda),A_i(\mathbf{X}^\lambda)\)の意味は\(\lambda\)番目の粒子が\(\beta\)番目の微小体積領域に入っていれば、それぞれ\(\phi^\beta,A_i^\beta\)の意味とする。

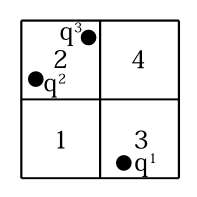
図10-2　

例えば図10-2のように系が微小領域1,2,3,4に分かれていて、電荷\(q^1,q^2,q^3\)がそれぞれ微小領域\(3,2,2\)に入っているとすると \[ \sum_{\lambda=1}^3 q^\lambda \phi(\mathbf{X}^\lambda)= q^1\phi^3+q^2\phi^2+q^3\phi^2 \] となる。 尚、このラグランジアン\(L\)は粒子の力学と違い、\(L=T-V\)ではない。 ラグランジアンの最後の項は\(\Delta V\to 0\)の極限で \[ \frac{\Delta V}{8\pi k}\sum_\beta\left(\left|\mathbf{E}^\beta\right|^2-\left|\mathbf{B}^\beta\right|^2\right) \quad \Longrightarrow \quad \frac{1}{8\pi k}\int\left|\mathbf{E}(\mathbf{r})\right|^2-\left|\mathbf{B}(\mathbf{r})\right|^2\;dV \] となる。偏微分\(\frac{\partial\, f}{\partial\, x}\)を短く\(\partial_xf\)、又は\(\partial_1f\)と書くことにする。\(\mathbf{E}\)は \[ \mathbf{E}=-\nabla \phi-\frac{1}{c}\frac{\partial\, \mathbf{A}}{\partial\, t} \] であり、その中の例えば\(\partial_x \phi\)は離散的に書くと \[ \partial_x \phi=\frac{\phi(x+\Delta x,y,z)-\phi(x,y,z)}{\Delta x} \] なので\(\nabla \phi\)の中には力学変数\(\phi\)が入っている。 \( \partial\, \mathbf{A}/\partial\, t \) は力学変数\(\mathbf{A}\)の時間微分なので\(\dot{\mathbf{A}}\)と書こう。又、\(\mathbf{B}\)は \[ \mathbf{B}=\nabla\times\mathbf{A} \] であり、\(\nabla\times\mathbf{A}\)は力学変数\(\mathbf{A}\)の空間微分なので、ここにも力学変数\(\mathbf{A}\)が含まれている。このラグランジアンでは 力学変数\(q\)に対応するのは\(X_i^\lambda,\phi^\beta,A_i^\beta\)であり、\(\dot{q}\)に対応するのが、その時間微分\(\dot{X}_i^\lambda\dot{A}_i^\beta\) である。この力学変数についてのラグランジュ方程式 \[ \frac{d}{dt}\left(\frac{\partial\, L}{\partial\, \dot{q}}\right)=\frac{\partial\, L}{\partial\, q} \] を作る。その式は 力学変数\(X\)に関してはローレンツ力の式(\ref{d5}) に、\(\phi\)に関しては、 マクスウェル方程式(\ref{d3}) に、\(\mathbf{A}\)に関しては、マクスウェル方程式(\ref{d4}) になる。そうなるようにラグランジアンを決めたのである。まとめると

定理10-1　 ラグランジアンを \[ L= \sum_{\lambda,i}\frac{1}{2}m^\lambda (\dot{X}_i^\lambda)^2- \sum_\lambda q^\lambda\phi(\mathbf{X}^\lambda)+ \sum_{\lambda,i}\frac{q^\lambda}{c}\dot{X}_i^\lambda A_i(\mathbf{X}^\lambda)+ \frac{\Delta V}{8\pi k}\sum_\beta\left(\left|\mathbf{E}^\beta\right|^2-\left|\mathbf{B}^\beta\right|^2\right) \] とすると、ラグランジュ方程式 \[ \frac{d}{dt}\left(\frac{\partial\, L}{\partial\, \dot{q}}\right)=\frac{\partial\, L}{\partial\, q} \] の、力学変数\(X\)成分はローレンツ力の式 \[ m\ddot{\mathbf{X}}=q\mathbf{E}+q\;\frac{\mathbf{\dot{X}}}{c}\times \mathbf{B} \] になる。\(\phi\)成分は、 マクスウェル方程式 \[ \nabla\cdot\mathbf{E}=4\pi k\rho \] になる。\(\mathbf{A}\)成分は、マクスウェル方程式 \[ \nabla\times \mathbf{B}=\frac{4\pi k}{c}\mathbf{J}+\frac{1}{c}\frac{\partial\, \mathbf{E}}{\partial\, t} \] になる。

10-2節　ラグランジュ方程式がローレンツ力の式、マクスウェル方程式になることの証明

さて、定理10-1を証明しよう。これは単純で煩雑な作業である。

(\(X\)成分)

まずX成分のラグランジュ方程式 \[ \frac{d}{dt}\left(\frac{\partial\, L}{\partial\, \dot{X}_i^\lambda}\right)=\frac{\partial\, L}{\partial\, X_i^\lambda} \] から計算していく。ラグランジアンは \[ L= \sum_{\lambda,i}\frac{1}{2}m^\lambda (\dot{X}_i^\lambda)^2- \sum_\lambda q^\lambda\phi(\mathbf{X}^\lambda)+ \sum_{\lambda,i}\frac{q^\lambda}{c}\dot{X}_i^\lambda A_i(\mathbf{X}^\lambda)+ \frac{\Delta V}{8\pi k}\sum_\beta\left(\left|\mathbf{E}^\beta\right|^2-\left|\mathbf{B}^\beta\right|^2\right) \] である。まず左辺だが、 \begin{equation} \frac{\partial\, L}{\partial\, \dot{X}_i^\lambda} =m^\lambda\dot{X}_i^\lambda+\frac{q^\lambda}{c}A_i(\mathbf{X}^\lambda) \label{9lambda} \end{equation} となる。そして、 \[ \frac{d}{dt}\left(\frac{\partial\, L}{\partial\, \dot{X}_i^\lambda}\right)= m^\lambda\ddot{X}_i^\lambda+\frac{q^\lambda}{c}\left(\sum_{j=1}^3\frac{\partial\, A_i(\mathbf{X}^\lambda)}{\partial\, X_j^\lambda}\dot{X}_j^\lambda+ \dot{A}_i(\mathbf{X}^\lambda) \right) \] となる。時間の全微分\(\frac{d}{dt}\)では力学変数である\(A_i^\beta\)も変化して\(\dot{A}_i\) も加えなければならないことに注意。一方右辺は \[ \frac{\partial\, L}{\partial\, X_i^\lambda}= -q^\lambda\frac{\partial\, \phi(\mathbf{X}^\lambda)}{\partial\, X_i^\lambda} + \frac{q^\lambda}{c}\sum_{j=1}^3\dot{X}_j^\lambda\frac{\partial\, A_j(\mathbf{X}^\lambda)}{\partial\, X_i^\lambda} \] である。だからラグランジュ方程式は \[ m^\lambda\ddot{X}_i^\lambda+\frac{q^\lambda}{c}\left(\sum_{j=1}^3\frac{\partial\, A_i(\mathbf{X}^\lambda)}{\partial\, X_j^\lambda}\dot{X}_j^\lambda+ \dot{A}_i(\mathbf{X}^\lambda) \right) = -q^\lambda\frac{\partial\, \phi(\mathbf{X}^\lambda)}{\partial\, X_i^\lambda} + \frac{q^\lambda}{c}\sum_{j=1}^3\dot{X}_j^\lambda\frac{\partial\, A_j(\mathbf{X}^\lambda)}{\partial\, X_i^\lambda} \] となる。整理すると \[ m^\lambda\ddot{X}_i^\lambda=q^\lambda\left( -\frac{\partial\, \phi(\mathbf{X}^\lambda)}{\partial\, X_i^\lambda}-\frac{1}{c}\dot{A}_i(\mathbf{X}^\lambda) \right) +\frac{q^\lambda}{c}\sum_{j=1}^3 \dot{X}_j^\lambda \left( \frac{\partial\, A_j(\mathbf{X}^\lambda)}{\partial\, X_i^\lambda}- \frac{\partial\, A_i(\mathbf{X}^\lambda)}{\partial\, X_j^\lambda} \right) \] となる。右辺の第1項は\(q^\lambda E_i(\mathbf{X}^\lambda)\) である。又、これは後で証明するが、一般に

補題10-1 \[ \sum_{j=1}^3\dot{x}_j \left( \frac{\partial\, A_j}{\partial\, x_i}- \frac{\partial\, A_i}{\partial\, x_j} \right)= (\mathbf{v}\times \mathbf{B})_i \] 成り立つ。ここで\(\mathbf{v}\)は点電荷の速度

だから\(X_i\)成分のラグランジュ方程式 \[ m^\lambda\ddot{X}_i^\lambda=q^\lambda E_i(\mathbf{X}^\lambda) +\frac{q^\lambda}{c}(\mathbf{v}^\lambda\times \mathbf{B})_i \] となり、ローレンツ力の式を表していることがわかる。

(\(\phi\)成分)

次に\(\phi\)成分のラグランジュ方程式 \[ \frac{d}{dt}\left(\frac{\partial\, L}{\partial\, \dot{\phi}^\beta}\right)=\frac{\partial\, L}{\partial\, \phi^\beta} \] を計算しよう。 ラグランジアンは \[ L= \sum_{\lambda,i}\frac{1}{2}m^\lambda (\dot{X}_i^\lambda)^2- \sum_\lambda q^\lambda\phi(\mathbf{X}^\lambda)+ \sum_{\lambda,i}\frac{q^\lambda}{c}\dot{X}_i^\lambda A_i(\mathbf{X}^\lambda)+ \frac{\Delta V}{8\pi k}\sum_\beta\left(\left|\mathbf{E}^\beta\right|^2-\left|\mathbf{B}^\beta\right|^2\right) \] である。 \(\dot{\phi}\)はラグランジアンに含まれていないので左辺は0である。右辺を計算しよう。最初に述べたように、\(\phi(\mathbf{X}^\lambda)\)というのは、\(\lambda\)番目の粒子が\(\beta\)番目の微小領域に入っていれば、その値は\(\phi^\beta\)であるということであった。だから\(\sum_\lambda q^\lambda\phi(\mathbf{X}^\lambda)\)を\(\phi^\beta\)で微分した値は\(\beta\)番目の領域に入っている電荷量となる。\(\beta\)番目の領域の電荷密度を\(\rho^\beta\)と書けば、\(\rho^\beta\Delta V\)がその領域の電荷量となるので \begin{equation} \frac{\partial\, }{\partial\, \phi^\beta}\sum_\lambda q^\lambda\phi(\mathbf{X}^\lambda) =\rho^\beta\Delta V \label{denka1} \end{equation} である。

最初に述べたように\(\partial_i \phi\)の中に\(\phi\)が含まれている。\(\partial_x\)に着目する。 \[ \frac{\partial\, \phi}{\partial\, x}(x,y,z)=\frac{\phi(x+\Delta x,y,z)-\phi(x,y,z)}{\Delta x} \] であるが、\(\beta\)番目の領域の\((\Delta x)\)だけ隣の領域を\((\beta+\Delta x)\)番と書くことにすると \[ \phi^\beta=\frac{\phi^{\beta+\Delta x}-\phi^\beta}{\Delta x} \qquad\qquad \phi^{\beta-\Delta x}=\frac{\phi^{\beta}-\phi^{\beta-\Delta x}}{\Delta x} \] である。だから \(\phi^\beta\)が含まれているのは \(\frac{\partial\, \phi^\beta}{\partial\, x}\)と\(\frac{\partial\, \phi^{(\beta-\Delta x)}}{\partial\, x}\) ということになる。そして \[ \frac{\partial\, \left(\partial_x\phi^\beta\right)}{\partial\, \phi^\beta}=-\frac{1}{\Delta x} \qquad\qquad \frac{\partial\, \left(\partial_x\phi^{(\beta-\Delta x)}\right)}{\partial\, \phi^\beta}=\frac{1}{\Delta x} \] である。そして \(E^\beta_x=-\partial_x\phi^\beta-\dot{A}^\beta_x/c\)で又\(E^{\beta-\Delta x}_x=-\partial_x\phi^{\beta-\Delta x}-\dot{A}^{\beta-\Delta x}_x/c\)ある。だから

\begin{eqnarray} \frac{\partial\,}{\partial\, \phi^\beta}\left[\sum_\gamma (E_x^\gamma)^2\right]&=& \frac{\partial (\partial_x\phi^\beta)}{\partial \phi^\beta}\frac{\partial}{\partial (\partial_x\phi^\beta)} \left(E_x^\beta\right)^2+ \frac{\partial (\partial_x\phi^{\beta-\Delta x})}{\partial \phi^\beta}\frac{\partial }{\partial (\partial_x\phi^{\beta-\Delta x})}\left(E_x^\beta\right)^2 \\ \notag &=&\left(-\frac{1}{\Delta x}\right)2E_x^\beta(-1)+\left(\frac{1}{\Delta x}\right)2E_x^{(\beta-\Delta x)}(-1)\notag \end{eqnarray}

となる。これは\(\Delta x\)が十分小さければ \[ 2\frac{\partial\, E_x^\beta}{\partial\, x} \] となる。 同様に \[ \frac{\partial\,}{\partial\, \phi^\beta}\left[\sum_\gamma (E_y^\gamma)^2\right]=2\frac{\partial\, E_y^\beta}{\partial\, y} \qquad\qquad \frac{\partial\,}{\partial\, \phi^\beta}\left[\sum_\gamma (E_z^\gamma)^2\right]=2\frac{\partial\, E_z^\beta}{\partial\, y} \] となる。 だから \[ \frac{\partial\,}{\partial\, \phi^\beta}\left[\sum_\gamma (\mathbf{E}^\gamma)^2\right] = 2\nabla\cdot\mathbf{E}^\beta \] となる。 だから \begin{equation} \frac{\partial\,}{\partial\, \phi^\beta}\left[\frac{\Delta V}{8\pi k}\sum_\gamma (\mathbf{E}^\gamma)^2\right] = \frac{\Delta V}{4\pi k}\nabla\cdot\mathbf{E}^\beta \label{denka2} \end{equation} となる。式(\ref{denka1})、(\ref{denka2})より、ラグランジュ方程式は \[ 0=-\rho^\beta\Delta V+\frac{\Delta V}{4\pi k}\nabla\cdot\mathbf{E}^\beta \] となる。すなわち \[ \nabla\cdot\mathbf{E}=4\pi k\rho \] となる。

(\(\mathbf{A}\)成分)

最後に\(\mathbf{A}\)成分のラグランジュ方程式 \[ \frac{d}{dt}\left(\frac{\partial\, L}{\partial\, \dot{A}_i^\beta}\right)=\frac{\partial\, L}{\partial\, A_i^\beta} \] を計算しよう。ラグランジアンは \[ L= \sum_{\lambda,i}\frac{1}{2}m^\lambda (\dot{X}_i^\lambda)^2- \sum_\lambda q^\lambda\phi(\mathbf{X}^\lambda)+ \sum_{\lambda,i}\frac{q^\lambda}{c}\dot{X}_i^\lambda A_i(\mathbf{X}^\lambda)+ \frac{\Delta V}{8\pi k}\sum_\beta\left(\left|\mathbf{E}^\beta\right|^2-\left|\mathbf{B}^\beta\right|^2\right) \] である。まず左辺を計算しよう。\(\dot{A}_i^\beta\)が含まれているのは\(E_i^\beta\)だけである。そして \(E^\beta_i=-\partial_i\phi^\beta-\dot{A}^\beta_i/c\)である。だから \[ \frac{\partial\,\left(E_i^\beta\right)^2 }{\partial\, \dot{A}_i^\beta}=-\frac{2E_i^\beta}{c} \] である。だから \begin{equation} \frac{\partial\, L}{\partial\, \dot{A}_i^\beta}= \frac{\partial\,}{\partial\, \dot{A}_i^\beta}\left[ \frac{\Delta V}{8\pi k}\sum_\gamma(\mathbf{E}^\gamma)^2\right] =-\frac{\Delta V}{4\pi k c}E_i^\beta \label{917} \end{equation} である。だから \begin{equation} \frac{d}{dt}\left(\frac{\partial\, L}{\partial\, \dot{A}_i(\mathbf{r}_\beta)}\right) = -\frac{1}{4\pi k c}\dot{E_i}^\beta\Delta V \label{denka3} \end{equation} である。

次に右辺を計算しよう。最初に述べたように、\(A_i(\mathbf{X}^\lambda)\)というのは、\(\lambda\)番目の粒子が\(\beta\)番目の微小領域に入っていれば、その値は\(A_i^\beta\)であるということであった。だから\(\sum_\lambda q^\lambda\dot{X}_i^\lambda A_i(\mathbf{X}^\lambda)\)を\(A_i^\beta\)で微分した値は \(\sum_{\beta\text{内}}q^\lambda \dot{X}_i^\lambda\)となる。\(\sum_{\beta\text{内}}\)は\(\beta\)番目の領域に入っている電荷について和を取ると言う意味である。\(\beta\)番目の領域の電流密度の\(i\)成分を\(J_i^\beta\)と書けば、\(\sum_{\beta\text{内}}q^\lambda \dot{X}_i^\lambda=J_i^\beta\Delta V\)である(注　\(\sum_{\beta\text{内}}q^\lambda \dot{X}_i^\lambda=J_i^\beta\Delta V\)となることは電磁気学の本を参照して欲しい)。 だから \begin{equation} \frac{\partial\, }{\partial\, A_i^\beta}\left[\sum_{\lambda,j} q^\lambda\dot{X}_j^\lambda A_j(\mathbf{X}^\lambda)\right] =J_i^\beta\Delta V \label{denryu1} \end{equation} である。

最初に述べたように、 \(\partial_jA_i\)の中に\(A_i\)が含まれている。\(\partial_x A_i\)に着目する。 \[ \partial_x A_i=\frac{A_i(x+\Delta x,y,z)-A_i(x,y,z)}{\Delta x} \] であり、\(\phi\)のときに導入した記号では \[ \partial_x A_i^\beta=\frac{A_i^{(\beta+\Delta x)}-A_i^\beta}{\Delta x} \qquad\qquad \partial_x A_i^{\beta-\Delta x}=\frac{A_i^{\beta}-A_i^{(\beta-\Delta x)}}{\Delta x} \] である。だから \(\partial_x A_i\)の中に\(A_i^\beta\)が含まれているのは\(\partial_x A_i^\beta\)と \(\partial_x A_i^{(\beta-\Delta x)}\)である。 そして \[ \frac{\partial\, \left(\partial\,_x A^\beta_i\right)}{\partial\, A^\beta_i}=-\frac{1}{\Delta x}\qquad\qquad \frac{\partial\, \left(\partial\,_x A^{(\beta-\Delta x)}_i\right)}{\partial\, A^\beta_i}=\frac{1}{\Delta x} \] である。 \(\partial_x A^\beta_i\)が含まれているのは\(\mathbf{B}^\beta\)である。\(\mathbf{B}\)の中には\(\partial_y A_i,\partial_z A_i\)も含まれているが、これは\(x\)の部分が\(y,z\)に置き換わるだけなので今は\(\partial_x A_i\)に含まれている\(A_i\)に関する微分のみを計算する。

\begin{eqnarray} \frac{\partial\, }{\partial\, A_i^\beta} \left[\sum_\gamma\left|\mathbf{B}^\gamma\right|^2\right] &=&\frac{\partial\, \left(\partial\,_x A^\beta_i\right)}{\partial\, A^\beta_i}\frac{\partial\, \left|\mathbf{B}^\beta\right|^2}{\partial\, \left(\partial_x A_i^\beta\right)} +\frac{\partial\, \left(\partial\,_x A^{(\beta-\Delta x)}_i\right)}{\partial\, A^\beta_i}\frac{\partial\, \left|\mathbf{B}^{(\beta-\Delta x)}\right|^2}{\partial\, \left(\partial_x A_i^{(\beta-\Delta x)}\right)} +\text{（\(y,z\)の項）} \notag\\ &=&-\frac{1}{\Delta x}\frac{\partial\, \left|\mathbf{B}^\beta\right|^2}{\partial\, \left(\partial_x A_i^\beta\right)} +\frac{1}{\Delta x}\frac{\partial\, \left|\mathbf{B}^{(\beta-\Delta x)}\right|^2}{\partial\, \left(\partial_x A_i^{(\beta-\Delta x)}\right)}+\text{（\(y,z\)の項）}\notag \end{eqnarray}

となる。ここで（\(y,z\)の項）というのは\(x\)の部分がそれぞれ\(y,z\)に置き換わった項のことである。\(\Delta x\)が十分小さければ、第1項は \[ -\frac{\partial\,}{\partial\, x}\left(\frac{\partial\, \left|\mathbf{B}^\beta\right|^2}{\partial\, \left(\partial_x A_i^\beta\right)} \right) \] となる。だから \[ \frac{\partial\,}{\partial\, A_i^\beta} \left[\sum_\gamma\left|\mathbf{B}^\gamma\right|^2\right] = -\sum_{j=1}^3\partial_j\left(\frac{\partial\,\left|\mathbf{B}^\beta\right|^2}{\partial\, \left(\partial_j A_i^\beta\right)}\right) \] となる。 後に示すように、一般に

補題10-2 \[ \sum_{j=1}^3\partial_j\left(\frac{\partial\,\left|\mathbf{B}\right|^2}{\partial\, \left(\partial_j A_i\right)}\right) =-2(\nabla\times\mathbf{B})_i \]

という式が成り立つ。だから \begin{equation} \frac{\partial\,}{\partial\, A_i^\beta}\left[\frac{\Delta V}{8\pi k}\sum_\gamma\left|\mathbf{B}^\gamma\right|^2\right] = \frac{\Delta V}{4\pi k}\left(\nabla\times\mathbf{B}^\beta\right)_i \label{denryu2} \end{equation} である。式(\ref{denryu1})、(\ref{denryu2})より、 \begin{equation} \frac{\partial\, L}{\partial\, A_i^\beta}= \frac{J_i^\beta}{c}\Delta V -\frac{1}{4\pi k}\left(\nabla\times\mathbf{B}^\beta\right)_i\Delta V \label{denryu3} \end{equation} となる。式(\ref{denka3})、(\ref{denryu3})より、ラグランジュ方程式は \[ -\frac{1}{4\pi k c}\dot{E_i}^\beta\Delta V = \frac{J_i^\beta}{c}\Delta V -\frac{1}{4\pi k}\left(\nabla\times\mathbf{B}^\beta\right)_i\Delta V \] となる。すなわち \[ \nabla\times \mathbf{B}=\frac{4\pi k}{c}\mathbf{J}+\frac{1}{c}\frac{\partial\, \mathbf{E}}{\partial\, t} \] となる。 後は補題10-1と10-2を示せば、定理10-1が示せたことになる。

(補題の証明)

補題10-1の \[ \sum_{j=1}^3 \dot{x}_j \left( \frac{\partial\, A_j}{\partial\, x_i}- \frac{\partial\, A_i}{\partial\, x_j} \right)= (\mathbf{v}\times \mathbf{B})_i \] を証明しよう。記号簡略化のため \[ F_{ij}\equiv \partial_i A_j-\partial\, _j A_i \] とおこう。\(F_{ij}\)は磁場テンソルと言われるものである。これの成分は、縦を\(i\)、横を\(j\)として \begin{equation} F_{ij}=\left( \begin{array}{ccc} 0&B_3&-B_2\\ -B_3&0&B_1\\ B_2&-B_1&0 \end{array}\right) \label{d26} \end{equation} となっていることはすぐわかろう。証明したいことは \[ \sum_{j=1}^3F_{ij}v_j=(\mathbf{v}\times \mathbf{B})_i \] である。式(\ref{d26})より \[ \sum_{j=1}^3F_{ij}v_j= \left( \begin{array}{ccc} 0&B_3&-B_2\\ -B_3&0&B_1\\ B_2&-B_1&0 \end{array}\right) \left( \begin{array}{c} v_1\\ v_2\\ v_3 \end{array}\right) = \left( \begin{array}{c} v_2B_3-v_3B_2\\ v_3B_1-v_1B_3\\ v_1B_2-v_2B_1 \end{array}\right) \] なので確かに\( \sum_{j=1}^3F_{ij}v_j=(\mathbf{v}\times \mathbf{B})_i \) になっている。これで補題10-1が証明ができたわけである。

次に補題10-2の \[ \sum_{j=1}^3 \partial_j\left(\frac{\partial\,|\mathbf{B}|^2}{\partial\, (\partial_j A_i)}\right) =-2(\nabla\times\mathbf{B})_i \] が成り立つことを証明しよう。\(|\mathbf{B}|^2\)と言うのは行列(\ref{d26})からわかるように \[ |\mathbf{B}|^2=\frac{1}{2}\sum_{k,l}(F_{kl})^2 \] である。\(\partial_j A_i\)が含まれているのは\(F_{ji}\)と\(F_{ij}\)であるから \[ \frac{\partial\, |\mathbf{B}|^2}{\partial\, (\partial_j A_i)}=F_{ji}-F_{ij}=2F_{ji} \] である。だから \[ \sum_{j=1}^3\partial_j\left(\frac{\partial\, |\mathbf{B}|^2}{\partial\, (\partial_j A_i)}\right) =2\sum_j \partial_j F_{ji}=-2\sum_j \partial_j F_{ij} \] となる。又、式(\ref{d26})から \[ \sum_{j=1}^3 \partial_j F_{ij}=(\nabla\times \mathbf{B})_i \] であることはすぐ確かめられる。だから \[ \sum_{j=1}^3\partial_j\left(\frac{\partial\, |\mathbf{B}|^2}{\partial\, (\partial_j A_i)}\right) = -2(\nabla\times \mathbf{B})_i \] である。 よって補題10-2が証明されたことになる。

10-3節　電磁場と荷電粒子のハミルトニアン

さて、いよいよ今のラグランジアン \begin{equation} L= \sum_{\lambda,i}\frac{1}{2}m^\lambda (\dot{X}_i^\lambda)^2- \sum_\lambda q^\lambda\phi(\mathbf{X}^\lambda)+ \sum_{\lambda,i}\frac{q^\lambda}{c}\dot{X}_i^\lambda A_i(\mathbf{X}^\lambda)+ \frac{\Delta V}{8\pi k}\sum_\beta\left(\left|\mathbf{E}^\beta\right|^2-\left|\mathbf{B}^\beta\right|^2\right) \label{iyo1} \end{equation} をルジャンドル変換してハミルトニアンを作ろう。それは \[ H=\sum_\alpha\frac{\partial\, L}{\partial\, \dot{q}_\alpha}\dot{q}_\alpha-L \] とするのであった。今の場合 \(\dot{\phi}\)はラグランジアンに含まれていないので\(\dot{X}_i^\lambda\)と\(\dot{A}_i^\beta\)に関してルジャンドル変換する。すなわちハミルトニアン\(H\)は \begin{equation} H= \sum_{i,\lambda}\frac{\partial\, L}{\partial\, \dot{X}_i^\lambda}\dot{X}_i^\lambda+ \sum_{i,\beta}\frac{\partial\, L}{\partial\, \dot{A}_i^\beta}\dot{A}_i^\beta-L \label{ha1} \end{equation} となる。\(X_i^\lambda,A_i^\beta,\)に対応する一般化運動量を\(u_i^\lambda,a_i^\beta\)と書こう。すなわち \[ u_i^\lambda\equiv \frac{\partial\, L}{\partial\, \dot{X}_i^\lambda} \qquad\qquad a_i^\beta\equiv\frac{\partial\, L}{\partial\, \dot{A}_i^\beta} \] である。これは式(\ref{9lambda}),(\ref{917})で計算したように \begin{equation} u_i^\lambda=m^\lambda\dot{X}_i^\lambda+\frac{q^\lambda}{c}A_i(\mathbf{X}^\lambda) \label{ha3} \end{equation} \begin{equation} a_i^\beta=-\frac{\Delta V}{4\pi c k}\;E_i^\beta \label{ha2} \end{equation} である。\(u_i^\lambda\)は通常の運動量である\(m^\lambda\dot{X}_i^\lambda\)と異なることに注意。 ハミルトニアンを計算しよう。 \begin{equation} \sum_{i,\lambda}u_i^\lambda\dot{X}_i^\lambda=\sum_{i,\lambda} m^\lambda\left(\dot{X}_i^\lambda\right)^2+\sum_{i,\lambda}\frac{q^\lambda}{c}\dot{X}_i^\lambda A_i(\mathbf{X}^\lambda) \label{ha5} \end{equation} となる。 又、 \begin{eqnarray} \sum_{i,\beta}a_i^\beta\dot{A}_i^\beta &=& -\frac{\Delta V}{4\pi c k}\sum_{i,\beta}E_i^\beta\cdot \dot{A}_i^\beta\notag\\ &=&-\frac{\Delta V}{4\pi c k}\sum_{i,\beta}E_i^\beta\cdot \left[-c\left(E_i^\beta+\partial_i\phi^\beta\right)\right]\notag\\ &=& \frac{\Delta V}{4\pi k}\sum_\beta\left(\left|\mathbf{E}^\beta\right|^2+\mathbf{E}^\beta\cdot\nabla\phi^\beta\right) \label{ha4} \end{eqnarray} となる。 式(\ref{iyo1}),(\ref{ha5}),(\ref{ha4})を式(\ref{ha1})に入れると

PDFファイルA4、158ページ、1.8MB

目次

序文

記号・用語

第1章

第2章

第3章

第4章

第5章

第6章

第7章

第8章

第9章

第10章

付録A

付録B

付録C

付録D

おわりに

となる。このハミルトニアンを\(p,q\)表示にしよう。すなわち 力学変数\(\dot{q}\)に対応する\(\dot{X}\)と\(\dot{A}\)を一般化運動量である\(u_i^\lambda,a_i^\beta\)で表してハミルトニアンから\(\dot{X}\)と\(\dot{A}\)を消そう。通常ハミルトニアンは\(p,q\)で表すものである。 式(\ref{ha3}),(\ref{ha2})より \[ m^\lambda\dot{X}_i^\lambda= u_i^\lambda-\frac{q^\lambda}{c}A_i(\mathbf{X}^\lambda) \] \[ E_i^\beta=-\frac{4\pi c k}{\Delta V}a_i^\beta \] である。又 \[ \left|\mathbf{B}^\beta\right|^2= \sum_{i,j}\frac{\left(\partial_i A_j^\beta-\partial_j A_i^\beta\right)^2}{2} \] である。 これらを使って、ハミルトニアンから\(\dot{X},\mathbf{E},\mathbf{B}\)を消去すると

となる。 さて第4-2節で述べたように \[ \frac{\partial\, H}{\partial\, p}=\dot{q} \] は\(\frac{\partial\, L}{\partial\, \dot{q}}=p\)を\(\dot{q}\)について解いたもの、すなわち\(p\)の定義式であり、 \[ \frac{\partial\, H}{\partial\, q}=-\dot{p} \] がラグランジュ方程式に対応することになるのであった。このことはルジャンドル変換の必然的結果である。だから\(\frac{\partial\, H}{\partial\, q}=-\dot{p}\)の \(X,\phi,\mathbf{A}\)成分はそれぞれ \begin{eqnarray} &&\frac{\partial\, H}{\partial\, X_i^\lambda}=-\dot{u}_i^\lambda \qquad\Longrightarrow\quad m\ddot{\mathbf{X}}^\lambda=q\mathbf{E}+q\;\frac{\mathbf{\dot{X}}^\lambda}{c}\times \mathbf{B}\notag\\ && \frac{\partial\, H}{\partial\, \phi^\beta}=0 \qquad\quad\Longrightarrow\quad \nabla\cdot \mathbf{E}=4\pi \rho\notag\\ && \frac{\partial\, H}{\partial\, A_i^\beta} =-\dot{a}_i^\beta \qquad\Longrightarrow\quad \nabla \times \mathbf{B}=\frac{4\pi k}{c}\mathbf{J}+\frac{1}{c}\dot{\mathbf{E}}\notag \end{eqnarray} を表していることになる。

さて、量子電磁気学を構成するためには \[ [\hat{X}_i^\lambda,\hat{u}_i^\lambda]=i\hbar \qquad\qquad [\hat{A}_i^\beta.\hat{a}_i^\beta]=i\hbar \] とするわけだが、\(\phi\)に対応する運動量がないところが残念なところである。

10-4節　ハミルトニアンがエネルギーとなること

さて、粒子の力学ではハミルトニアンは例外的な場合を除いて系のエネルギーと一致していた(定理4-5)。一方、式(\ref{ha6})を見ると、これはエネルギーと一致していないように思える。というのは電磁場と荷電粒子のエネルギー\(E\)は \begin{equation} E= \sum_{\lambda,i}\frac{1}{2}m_\lambda (\dot{X}_i^\lambda)^2+ \frac{1}{8\pi k}\int|\mathbf{E}(\mathbf{r})|^2+|\mathbf{B}(\mathbf{r})|^2\;dV \label{ha41} \end{equation} だからである。余分な項として \[ \sum_\lambda q^\lambda\phi(\mathbf{X}^\lambda)+ \frac{1}{4\pi k}\int\mathbf{E}(\mathbf{r})\cdot\nabla\phi(\mathbf{r}) \;dV \] がある。ところがこれは系がマクスウェル方程式を満たしているなら0になる。それを示そう。 部分積分により \[ \frac{1}{4\pi k}\int\mathbf{E}(\mathbf{r})\cdot\nabla\phi(\mathbf{r}) \;dV =\int \mathbf{E}\; \phi \;d\mathbf{s}-\int \nabla\cdot \mathbf{E}\; \phi \;dV \] となる。\(\int \mathbf{E} \;\phi\; d\mathbf{s}\)というのは面積分である。これは\(\mathbf{E},\phi\)が有限領域に限られるなら\(0\)になる。\(\nabla\cdot \mathbf{E}=4\pi k\rho\)なので、結局 \[ \frac{1}{4\pi k}\int\mathbf{E}(\mathbf{r})\cdot\nabla\phi(\mathbf{r}) \;dV=-\int\rho \;\phi\; dV \] となる。一方\(\sum_\lambda q^\lambda\phi(\mathbf{X}^\lambda)\)だが、ある\(\Delta V\)の領域に入っている電荷量は\(\rho \Delta V\)であり、すべての荷電粒子\(\lambda\)について和をとるということは全空間で和とることだから \[ \int\rho \;\phi\; dV \] に等しい。だから余分な項は消え、ハミルトニアンは古典電磁気学のエネルギーと等しくなる。すなわち

だが注意すべきことは、ハミルトニアンが古典電磁気学のエネルギー(\ref{ha41})に等しいからといって、式(\ref{ha41})をハミルトニアンにしてしまってはいけない。というのはハミルトンの正準方程式の一つである \[ \frac{\partial\, H}{\partial\, \phi^\beta}=0 \quad \Longleftrightarrow\quad \nabla\cdot \mathbf{E}=4\pi \rho \] を式(\ref{ha6})に代入すれば式(\ref{ha41})に等しくなるのであり、もしこの結果を先に代入してしまっては、肝心のこの式が出てこないのである。 今は系を有限領域に限ったが、有限領域に限らなければハミルトニアンはエネルギーに等しくならないことに注意。

10-5節　相対論への修正

今までは非相対論的に扱ってきたが、それを相対論的なものに修正しよう。 電磁気学において非相対論的扱いと相対論的扱いで異なるのはローレンツ力の式だけである。マクスウェル方程式は同じである。しかし、だからと言って、相対論によって電磁気学が修正を要しなかったとは思わないでもらいたい。というのはローレンツ力の式は電場と磁場の定義も含んでおり、ローレンツ力の式が修正を受けるということは、電場、磁場の定義も修正を受けるということだからである。

さて話を非相対論の場合と相対論の場合を対比しながら進めていこう。ローレンツ力の式はそれぞれ

\begin{eqnarray} &&\text{非相対論}\qquad m\ddot{\mathbf{X}}=q\mathbf{E}+q\;\frac{\mathbf{\dot{X}}}{c}\times \mathbf{B} \label{hhh}\\ &&\text{相対論}\qquad \frac{d}{dt}\left(\frac{m\dot{\mathbf{X}}}{\sqrt{1-\frac{v^2}{c^2}}}\right)=q\mathbf{E}+q\;\frac{\mathbf{\dot{X}}}{c}\times \mathbf{B} \label{so2} \end{eqnarray}

である。非相対論でのローレンツ力の式を表す式は \[ \frac{d}{dt}\left(\frac{\partial\, L}{\partial\, \dot{X}_i^\lambda}\right)=\frac{\partial\, L}{\partial\, X_i^\lambda} \] であった。この式が相対論でのローレンツ力の式(\ref{so2}) になるようにしたい。そこで非相対論的ラグランジアンでの\(\frac{1}{2}m\dot{X}_i^2\)の部分を \[ \sum_i \frac{1}{2}m\dot{X}_i^2\quad \Longrightarrow \quad -mc^2\sqrt{1-\frac{v^2}{c^2}} \] と置き換えよう。すなわちラグランジアンを

\begin{eqnarray} &&\text{非相対論}\qquad L=\sum_{i,\lambda}\frac{1}{2}m(\dot{X}_i^\lambda)^2+\text{[その他]} \notag\\ &&\text{相対論}\qquad L=-\sum_{\lambda}m^\lambda c^2\sqrt{1-\frac{(v^\lambda)^2}{c^2}}+\text{[その他]}\notag \end{eqnarray}

と修正しよう。ここで\(v\)は粒子の速度であり、\(v^2=\sum_i \dot{X}_i^2\)のことである。[その他]と書いた部分は非相対論と相対論で同じである項である。さてそうすると \begin{eqnarray} &&\text{非相対論}\qquad \frac{\partial\, L}{\partial\, \dot{X}_i^\lambda} =m^\lambda\dot{X}_i+\frac{q^\lambda}{c}A_i(\mathbf{X}^\lambda) \notag\\ &&\text{相対論}\qquad \frac{\partial\, L}{\partial\, \dot{X}_i^\lambda} =\frac{m^\lambda\dot{X}_i^\lambda}{\sqrt{1-\frac{(v^\lambda)^2}{c^2}}}+\frac{q^\lambda}{c}A_i(\mathbf{X}^\lambda) \label{sate} \end{eqnarray} となる。 \(\displaystyle\frac{\partial\, L}{\partial\, X_i^\lambda}\) は非相対論と相対論で同じである。だからラグランジュ方程式は非相対論での \[ \frac{d}{dt}\left(m^\lambda\dot{X}_i\right) \] の部分が相対論では \[ \frac{d}{dt}\left(\frac{m^\lambda\dot{X}_i^\lambda}{\sqrt{1-\frac{(v^\lambda)^2}{c^2}}}\right) \] に置き換わるだけである。 それゆえ非相対論でローレンツ力の式(\ref{hhh})がラグランジュ方程式から導かれるなら、相対論的なラグランジアンでローレンツ力の式(\ref{so2})がラグランジュ方程式から導かれるのがわかろう。\(\phi,\mathbf{A}\)に関わる項は全く修正されないので、相対論的ラグランジアンでもマクスウェル方程式が導かれる。ここで改めて相対論的ラグランジアンを書くと

である。さてこれをルジャンドル変換してハミルトニアンを作ろう。 すなわち \[ H=\sum_{i,\lambda}u_i^\lambda\dot{X}_i^\lambda+ \sum_{i,\beta}a_i^\beta\dot{A}_i^\beta -L \] とするわけである。ここで非相対論のときと変わったのは \(u_i^\lambda\)と\(L\)である。\(u_i^\lambda\)は \begin{eqnarray} &&\text{非相対論}\qquad u_i^\lambda =m^\lambda\dot{X}_i+\frac{q^\lambda}{c}A_i(\mathbf{X}^\lambda) \notag\\ &&\text{相対論}\qquad u_i^\lambda =\frac{m^\lambda\dot{X}_i^\lambda}{\sqrt{1-\frac{(v^\lambda)^2}{c^2}}}+\frac{q^\lambda}{c}A_i(\mathbf{X}^\lambda) \label{tai2} \end{eqnarray} となり\(L\)は前述の式(\ref{zenj})のとおりである。その点に注意して、非相対論のハミルトニアンと相対論のハミルトニアンを比較すると \begin{eqnarray} &&\text{非相対論}\qquad H=\sum_{i,\lambda}\left[m^\lambda(\dot{X}_i^\lambda)^2-\frac{1}{2}m^\lambda(\dot{X}_i^\lambda)^2\right]\quad+\text{[その他]} \notag\\ &&\text{相対論}\qquad H=\sum_{\lambda}\left[\frac{m^\lambda\left(v^\lambda\right)^2}{\sqrt{1-\frac{\left(v^\lambda\right)^2}{c^2}}}+ m^\lambda c^2\sqrt{1-\frac{(v^\lambda)^2}{c^2}}\right]\quad+\text{[その他]}\notag \end{eqnarray} [その他]とあるのは非相対論と相対論で同じ項ということ。 これを計算すると \begin{eqnarray} &&\text{非相対論}\qquad H=\sum_{i,\lambda}\left[\frac{1}{2}m^\lambda(\dot{X}_i^\lambda)^2\right]\quad+\text{[その他]} \notag\\ &&\text{相対論}\qquad H=\sum_{\lambda}\left[\frac{m^\lambda c^2}{\sqrt{1-\frac{\left(v^\lambda\right)^2}{c^2}}}\right]\quad+\text{[その他]}\notag \end{eqnarray} となる。 よって相対論的ハミルトニアンは 非相対論での\(\frac{1}{2}m^\lambda(\dot{X}_i^\lambda)^2\)の部分を \[ \sum_{i,\lambda}\left[\frac{1}{2}m^\lambda(\dot{X}_i^\lambda)^2\right] \quad \Longrightarrow \quad \sum_{\lambda}\left[\frac{m^\lambda c^2}{\sqrt{1-\frac{\left(v^\lambda\right)^2}{c^2}}}\right] \] と置き換えれば良い。だから式(\ref{ha6})でこの置き換えをすると

となる。

ハミルトニアンを\(p,q\)で表示しよう。非相対論でのハミルトニアンとは \(\frac{m^\lambda c^2}{\sqrt{1-\frac{(v^\lambda)^2}{c^2}}}\)の部分が異なるだけである。一般化運動量は式(\ref{tai2})より \begin{equation} u_i^\lambda =\frac{m^\lambda\dot{X}_i^\lambda}{\sqrt{1-\frac{\left(v^\lambda\right)^2}{c^2}}}+\frac{q^\lambda}{c}A_i(\mathbf{X}^\lambda) \label{so51} \end{equation} である。これ を使って\(\dot{X}_i^\lambda\)を\(u_i^\lambda\)で表せばよいのだが、これを愚直に\(\dot{X}_i^\lambda\)について解くのはめんどうである。それで相対論でよく知られた恒等式 \begin{equation} c\sqrt{m^2c^2+p^2}=\frac{mc^2}{\sqrt{1-\frac{v^2}{c^2}}} \label{yoku} \end{equation} を使おう。ここでの\(p\)は通常の運動量であり \[ p=\frac{mv}{\sqrt{1-\frac{v^2}{c^2}}} \] である。通常の運動量とハミルトニアンでの一般化運動量が異なることに注意。式(\ref{so51})より \[ u_i-\frac{q}{c}A_i(\mathbf{X}) = \frac{m\dot{X}_i}{\sqrt{1-\frac{v^2}{c^2}}} \] である。ここでは粒子の番号の指標を省いた。だから \[ \sum_{i=1}^3\left(u_i-\frac{q}{c}A_i(\mathbf{X})\right)^2 = \left(\frac{mv}{\sqrt{1-\frac{v^2}{c^2}}}\right)^2 =p^2 \] である。これを式(\ref{yoku})に入れると \[ c\sqrt{m^2c^2+\sum_i\left(u_i-\frac{q}{c}A_i(\mathbf{X})\right)^2} = \frac{mc^2}{\sqrt{1-\frac{v^2}{c^2}}} \] となる。これをハミルトニアン(\ref{oki3})の第1項に代入する。第1項以外は非相対論と相対論で同じである。よってハミルトニアンの\(p,q\)表示では

となるわけである。

10-6節　まとめ

荷電粒子と電磁場のハミルトニアンを作るのは量子電磁気学のためである。そのハミルトニアンを作るためにラグランジアンを作るのである。力学変数\(q\)は粒子の位置、電磁場のポテンシャル\(\phi\)、ベクトルポテンシャル\(\mathbf{A}\)である。\(\phi,\mathbf{A}\)は場所ごとに力学変数が存在することになる。 ラグランジアンは ラグランジュ方程式がローレンツ力の式とマクスウェル方程式を表すように作る。それが\(q,\dot{q}\)表示では

であり、\(p,q\)表示では

である。\(u_i^\lambda\)は粒子の位置座標\(X_i^\lambda\)に対応する一般化運動量である。\(a_i^\beta\)はベクトルポテンシャル\(A_i^\beta\)に対応する一般化運動量である。ルジャンドル変換の必然的結果として正準方程式 \[ \frac{\partial\, H}{\partial\, q}=-\dot{p} \] はラグランジュ方程式\(\displaystyle\dot{p}=\frac{\partial\, L}{\partial\, q}\)を表すことになるので、ローレンツ力とマクスウェル方程式を表すことになる。 このハミルトニアンは無限遠方で電磁場が0になるならエネルギーに等しい(定理10-2)。 量子電磁気学を構成するためには演算子の交換関係 \[ [\hat{q},\hat{p}]=i\hbar \] を設定する。しかし\(\phi\)に対応する一般化運動量がないので\(\phi\)に関してはできない。

今までは非相対論での話である。正しいのは相対論なのだから、相対論へ修正する。 非相対論と相対論で修正されるのはローレンツ力の式だけである。マクスウェル方程式は変わらない。形式的にはマクスウェル方程式は変わらないが、物理的意味は異なる。というのは、ローレンツ力の式が電磁場の定義式にもなっているからである。ラグランジュ方程式がローレンツ力とマクスウェル方程式を表すようにラグランジアンを作る。そうなるためには 非相対論的ラグランジアンでの\(\frac{1}{2}m\dot{X}_i^2\)の部分を \[ \sum_i \frac{1}{2}m\dot{X}_i^2\quad \Longrightarrow \quad -mc^2\sqrt{1-\frac{v^2}{c^2}} \] と置き換えて

とすればよい。 あとはルジャンドル変換してハミルトニアンを作る。それは 非相対論での\(\frac{1}{2}m^\lambda(\dot{X}_i^\lambda)^2\)の部分を \[ \left[\frac{1}{2}m^\lambda(\dot{X}_i^\lambda)^2\right] \quad \Longrightarrow \quad \left[\frac{m^\lambda c^2}{\sqrt{1-\frac{\left(v^\lambda\right)^2}{c^2}}}\right] \] と置き換えた

が相対論でのハミルトニアンとなる。\(p,q\)表示では

となる。正準方程式の \[ \frac{\partial\, H}{\partial\, q}=-\dot{p} \] がローレンツ力とマクスウェル方程式を表すことは非相対論のときと変わらない。これはルジャンドル変換の必然的結果だからである。