第3章 ラグランジュ方程式の幾何学的意味
この章は著者個人の趣味的な考察なので気軽に飛ばしてもらえばよい。 今までラグランジュ方程式を導出し、その例を見てきた。ここではラグランジュ方程式の幾何学的意味を考察したい。 ニュートンの運動方程式というのは 元々加速度は力に比例し、質量に反比例する。そして力の向きと等しい。というもので座標で表されたものではなく、図3-1のように幾何学的な
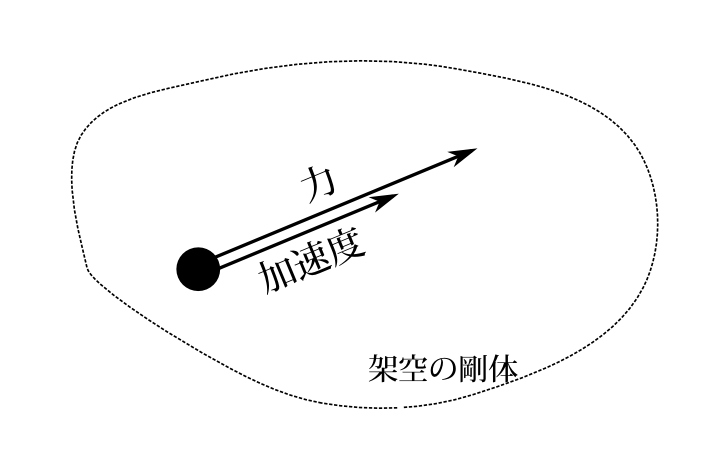
図3-1 ニュートンの運動法則は加速度は力に比例し、向きが等しいというもので、座標によるものではない。
ものである。ベクトル記号で書けば \[ m\ddot{\mathbf{r}}=\mathbf{F} \] というものである。 その法則を様々な一般座標で表したものがラグランジュ方程式である。ラグランジュ方程式を導く際に、直交座標でのニュートンの運動方程式 \[ m_i\ddot{x}_i=F_i \] に\(\frac{\partial\, x_i}{\partial\, q_\alpha}\)を掛けて\(i\)で和をとるという方法をとった。その和をとった式が一般座標でのラグランジュ方程式なわけである。 しかしながら直交座標も一般座標の1つであり、特別視するいわれはないような気がする。そこで直交座標を特別視せずにラグランジュ方程式の意味というものを考えてみたいわけである。
3-1節 直交座標
1粒子の系を考える。ニュートンの法則の座標によらない表現として \(\mathbf{r}\)を位置ベクトルとすると \begin{equation} m\ddot{\mathbf{r}}=\mathbf{F} \label{lahon1} \end{equation} と表される。位置ベクトルは単位直交基底を用いて \[ \mathbf{r}=x_1\mathbf{e}_1+x_2\mathbf{e}_2+x_3\mathbf{e}_3 \] と表される。これを時間で2回微分して、ベクトルの和差が順序を入れ替えることができることができる性質を使うと \begin{equation} \ddot{\mathbf{r}}=\ddot{x}_1\mathbf{e}_1+\ddot{x}_2\mathbf{e}_2+\ddot{x}_3\mathbf{e}_3 \label{lahon3} \end{equation} となる。力\(\mathbf{F}\)も同様に単位直交基底で分解して \begin{equation} \mathbf{F}=F_1\mathbf{e}_1+F_2\mathbf{e}_2+F_3\mathbf{e}_3 \label{lahon4} \end{equation} とする。式(\ref{lahon3})(\ref{lahon4})を式(\ref{lahon1})に入れる。各基底の係数は等しくならなければならないので \[ m\ddot{x}_1=F_1\qquad m\ddot{x}_2=F_2\qquad m\ddot{x}_3=F_3 \] でなければならない。 これが直交座標での運動方程式が成り立つ根拠である。この式はこの直交座標でのラグランジュ方程式でもある。さてこの式は \[ \mathbf{e}_1\cdot m\ddot{\mathbf{r}}=\mathbf{e}_1\cdot \mathbf{F} \qquad \mathbf{e}_2\cdot m\ddot{\mathbf{r}}=\mathbf{e}_2\cdot \mathbf{F} \qquad \mathbf{e}_3\cdot m\ddot{\mathbf{r}}=\mathbf{e}_3\cdot \mathbf{F} \] と同じことである。すなわち\(m\ddot{\mathbf{r}}\)を\(x_i\)軸へ正射影したものと、力をそれへ正射影したものは等しいという式である。正射影というのは図3-2のようにベクトルの視点と終点からその軸へ垂線を下ろした影の部分のことである。
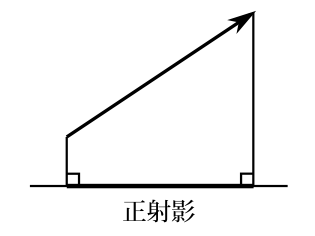
図3-2 ベクトルの視点と終点からその軸へ垂線を下ろした影の部分を正射影という。
単位直交座標のラグランジュ方程式とは\(m\ddot{\mathbf{r}}=\mathbf{F}\)を各軸に正射影したもの、すなわち\(\mathbf{e}_i\cdot m \ddot{\mathbf{r}}=\mathbf{e}_i\cdot \mathbf{F}\)である。
と言えるわけである。
3-2節 一般座標・1粒子
次に一般座標でのラグランジュ方程式の幾何学的意味を考えよう。まず1粒子の場合を考える。一般座標\(q_\alpha\)のラグランジュ方程式は \begin{equation} \sum_{i=1}^3\frac{\partial\, x_i}{\partial\, q_\alpha}m_i\ddot{x}_i=\sum_{i=1}^3\frac{\partial\, x_i}{\partial\, q_\alpha}F_i \label{lahon11} \end{equation} であった。一般座標\(q_\alpha\)が1変化したあたりの位置\(\mathbf{r}\)の変化量を\(\mathbf{e}_\alpha\)と書こう。すなわち \[ \mathbf{e}_\alpha\equiv\frac{\partial\, \mathbf{r}}{\partial\, q_\alpha} \] である。 \[ \mathbf{r}=x_1\mathbf{e}_1+x_2\mathbf{e}_2+x_3\mathbf{e}_3 \] なので \[ \mathbf{e}_\alpha=\frac{\partial\, x_1}{\partial\, q_\alpha}\mathbf{e}_1+\frac{\partial\, x_2}{\partial\, q_\alpha}\mathbf{e}_2+\frac{\partial\, x_3}{\partial\, q_\alpha}\mathbf{e}_3 \] である。一方\(m\ddot{\mathbf{r}}\)は直交成分に分解すると \[ m\ddot{\mathbf{r}}=m\ddot{x}_1\mathbf{e}_1+m\ddot{x}_2\mathbf{e}_2+m\ddot{x}_3\mathbf{e}_3 \] であった。又\(\mathbf{F}\)は \[ \mathbf{F}=F_1\mathbf{e}_1+F_2\mathbf{e}_2+F_3\mathbf{e}_3 \] である。だから \[ \mathbf{e}_\alpha\cdot m\ddot{\mathbf{r}}=\sum_i\frac{\partial\, x_i}{\partial\, q_\alpha}m_i\ddot{x}_i \qquad \mathbf{e}_\alpha\cdot\mathbf{F}=\sum_i\frac{\partial\, x_i}{\partial\, q_\alpha}F_i \] である。だからラグランジュ方程式(\ref{lahon11})は \begin{equation} \mathbf{e}_\alpha\cdot m\ddot{\mathbf{r}}=\mathbf{e}_\alpha\cdot\mathbf{F} \label{lahon12} \end{equation} ということである。これを\(q_\alpha\)座標系で表現したものが\(q_\alpha\)成分のラグランジュ方程式である。式(\ref{lahon12})は\(m\ddot{\mathbf{r}}=\mathbf{F}\)という式を\(\mathbf{e}_\alpha\)の方向に正射影して\(|\mathbf{e}_\alpha|\)を掛けたものになっている。本質的には正射影したものである(図3-3)。
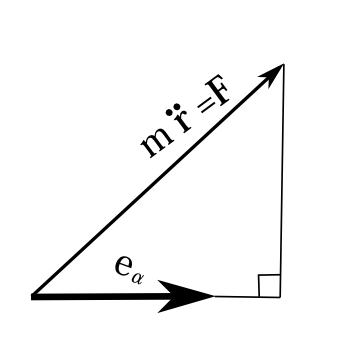
図3-3 1粒子のラグランジュ方程式は\(m\mathbf{\ddot{r}}=\mathbf{F}\)の正射影×\(|\mathbf{e}_\alpha|\)倍である。
だから
定理3-1 1粒子の\(q_\alpha\)成分のラグランジュ方程式というのは\(m\ddot{\mathbf{r}}=\mathbf{F}\)という式を、座標\(q_\alpha\)が増える方向に正射影し、両辺を\(|\mathbf{e}_\alpha|\)倍したものである。
と言える。これは直交座標でもあてはまることである。式(\ref{lahon11})というのは\(m\ddot{\mathbf{r}}=\mathbf{F}\)をいったん直交成分へ正射影して、それを再び\(\mathbf{e}_\alpha\)方向へ正射影して\(|\mathbf{e}_\alpha|\)倍したものなわけである。もちろんいきなり\(\mathbf{e}_\alpha\)へ正射影しても同じ式が得られる。
例3-1
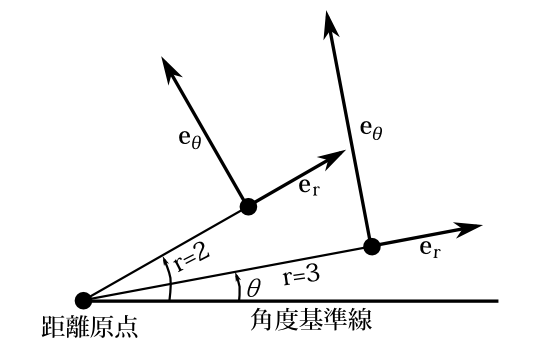
図3-4 \(r=2,r=3\)のときの\(\mathbf{e}_r,\mathbf{e}_\theta\)
例として2次元極座標を考えよう。 位置ベクトルを \[ \mathbf{r}=r\cos\theta \cdot \mathbf{e}_x+r\sin\theta\cdot \mathbf{e}_y \] と表すと、\(r\)に対応する\(\mathbf{e}_r\)は \[ \mathbf{e}_r=\cos\theta\cdot \mathbf{e}_x+\sin\theta\cdot \mathbf{e}_y \] であるので、\(|\mathbf{e}_r|=1\)である。だから\(r\)成分のラグランジュ方程式というのは\(m\ddot{\mathbf{r}}=\mathbf{F}\)の\(r\)方向への正射影そのままである。だから\(r\)方向の一般化力\(f_r\)というのは\(r\)方向の力の大きさを表している。これが2-5節の例2-7で\(f_r\)が拘束力であると述べた理由である。又\(\theta\)に対応する\(\mathbf{e}_\theta\)は \[ \mathbf{e}_\theta=-r\sin\theta\cdot\mathbf{e}_x+r\cos\theta\cdot \mathbf{e}_y \] なので\(|\mathbf{e}_\theta|=r\)である。だから\(\theta\)成分のラグランジュ方程式というのは\(m\ddot{\mathbf{r}}=\mathbf{F}\)の\(\theta\)方向へ正射影して両辺に\(r\)を掛けたものになる。図3-4に\(r=2,r=3\)のときの\(\mathbf{e}_r,\mathbf{e}_\theta\)を図示した。【例終】
例3-2
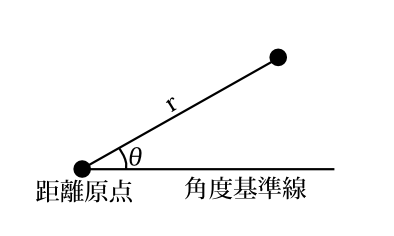
図3-5 極座標。直交座標という概念自体が不要である。
定理3-1の考えを使って直接正射影してラグランジュ方程式を導こう。いっさい直交座標という概念を除去して導こうというわけである。極座標というのは図3-5のように\(r\)を測る原点があり、角度を測る原点から伸びた基準線があればよいわけである。だから直交座標の概念は不要である。 極座標の場合\(\mathbf{e}_r,\mathbf{e}_\theta\)とも粒子の運動に伴って変化するので、直交座標へ正射影してから\(\mathbf{e}_r,\mathbf{e}_\theta\)方向へ正射影する方法より面倒である。
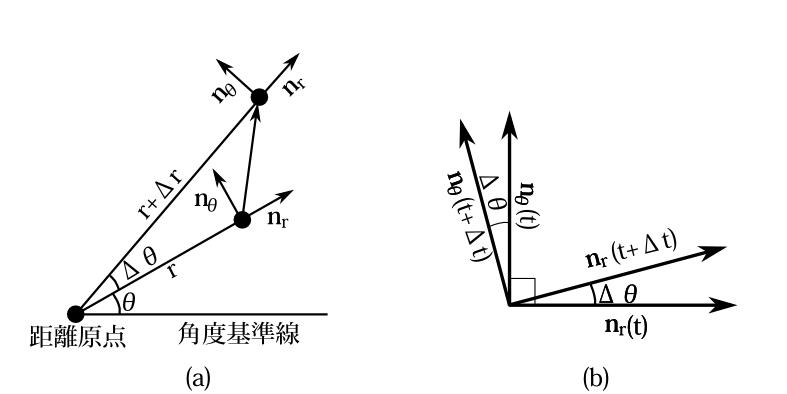
図3-6 (a):\(\mathbf{n}_r=\frac{\mathbf{e}_r}{|\mathbf{e}_r|}\quad \mathbf{n}_\theta=\frac{\mathbf{e}_\theta}{|\mathbf{e}_\theta|}\)、\(\mathbf{n}_r\)と\(\mathbf{n}_\theta\)は単位ベクトルで粒子の位置(角度)によって向きを変える。 (b):\(\mathbf{n}_r\)と\(\mathbf{n}_\theta\)の関係。\(\Delta \theta\)だけ粒子が動くと\(\mathbf{n}_r\)と\(\mathbf{n}_\theta\)は\(\Delta \theta\)だけ回転する。
計算のため \[ \mathbf{n}_r=\frac{\mathbf{e}_r}{|\mathbf{e}_r|}\qquad \mathbf{n}_\theta=\frac{\mathbf{e}_\theta}{|\mathbf{e}_\theta|} \] という単位ベクトルを導入しよう。時間\(t\)でのそれぞれの値を\(r(t),\theta(t),\dot{r}(t),\dot{\theta}(t),\mathbf{n}_r(t),\mathbf{n}_\theta(t)\)と書くと、時間\(t\)での 速度\(\mathbf{v}\)は \[ \mathbf{v}(t)=\dot{r}(t)\mathbf{n}_r(t)+r(t)\dot{\theta}(t)\mathbf{n}_\theta(t) \] である。これを成分表示で \[ \mathbf{v}(t)= \left( \begin{array}{l} \dot{r}(t)\\ r(t)\dot{\theta}(t) \end{array} \right) \] と書こう。時間が\(t\)から\(\Delta t\)増える間に角度は\(\Delta \theta\)増えるとしよう。時間\(t+\Delta t\)での \(\mathbf{n}_r(t+\Delta t),\mathbf{n}_\theta(t+\Delta t)\)は図3-6のように、時間\(t\)でのそれより角度が\(\Delta \theta\)回転している。 だから\(t+\Delta t\)での速度\(\mathbf{v}(t+\Delta t)\)は\(\mathbf{n}_r(t),\mathbf{n}_\theta(t)\)を基底とした成分表示では \begin{eqnarray} \mathbf{v}(t+\Delta t)&=& \left( \begin{array}{rr} \cos\Delta \theta&-\sin\Delta \theta\\ \sin\Delta \theta&\cos\Delta \theta \end{array} \right) \left( \begin{array}{l} \dot{r}(t+\Delta t)\notag\\ r(t+\Delta t)\dot{\theta}(t+\Delta t) \end{array} \right)\\ &=& \left( \begin{array}{c} \cos\Delta \theta\cdot\dot{r}(t+\Delta t)-\sin\Delta \theta\cdot r(t+\Delta t)\dot{\theta}(t+\Delta t)\\ \sin\Delta \theta\cdot \dot{r}(t+\Delta t)+\cos\Delta \theta\cdot r(t+\Delta t)\dot{\theta}(t+\Delta t) \end{array} \right)\notag \end{eqnarray} となる。だから \begin{equation} \frac{\mathbf{v}(t+\Delta t)-\mathbf{v}(t)}{\Delta t}= \frac{1}{\Delta t} \left( \begin{array}{l} \cos\Delta \theta\cdot\dot{r}(t+\Delta t)-\sin\Delta \theta\cdot r(t+\Delta t)\dot{\theta}(t+\Delta t)-\dot{r}(t)\\ \sin\Delta \theta\cdot \dot{r}(t+\Delta t)+\cos\Delta \theta\cdot r(t+\Delta t)\dot{\theta}(t+\Delta t)-r(t)\dot{\theta}(t) \end{array} \right) \label{lahon21} \end{equation} となり、\(\Delta t\to 0\)の極限では \begin{equation} \dot{\mathbf{v}}=\left( \begin{array}{c} \ddot{r}-r\dot{\theta}^2\\ 2\dot{r}\dot{\theta}+r\ddot{\theta} \end{array} \right) \label{lahon22} \end{equation} となる。式(\ref{lahon21})から(\ref{lahon22})へ至った計算の詳細は省くが、微小量の1次の項まで考慮すれば容易に導けると思う。さてこの加速度の\(r\)方向への正射影は\(\ddot{r}-r\dot{\theta}^2\)であり\(|\mathbf{e}_r|=1\)なので\(r\)成分のラグランジュ方程式は \begin{equation} m(\ddot{r}-r\,\dot{\theta}^2)=f_r \label{lahon222} \end{equation} である。\(f_r\)は\(r\)成分の一般化力。又、加速度の\(\theta\)方向への正射影は \((2\dot{r}\dot{\theta}+r\ddot{\theta})\) であり、\(|\mathbf{e}_\theta|=r\)なので\(\theta\)成分のラグランジュ方程式は \begin{equation} m(2\,r\,\dot{r}\,\dot{\theta}+r^2\ddot{\theta})=f_\theta \label{lahon23} \end{equation} である。\(f_\theta\)は\(\theta\)成分の一般化力。式(\ref{lahon222})(\ref{lahon23})とも以前に導いた2-3節の式(12)(13)と一致している。【例終】
3-3節 多粒子系
図3-7 各質点ごとに\(\mathbf{e}_\alpha^1\equiv \frac{\partial\,\mathbf{r}^1}{\partial\, q_\alpha},\mathbf{e}_\alpha^2\equiv \frac{\partial\,\mathbf{r}^2}{\partial\, q_\alpha},\cdots\)を作る。
次に粒子が幾つかある場合のラグランジュ方程式 \[ \sum_i\frac{\partial\, x_i}{\partial\, q_\alpha}m_i\ddot{x}_i=\sum_i\frac{\partial\, x_i}{\partial\, q_\alpha}F_i \] を考察する。1つ1つの粒子に番号をつけ、 \(\lambda\)番目の質量、位置、力を\(m^\lambda,\mathbf{r}^\lambda,\mathbf{F}^\lambda\)と書く。 そして座標\(q_\alpha\)が1増えるあたりの\(\lambda\)番目の粒子の位置の変化量を\(\mathbf{e}_\alpha^\lambda\)とする。すなわち \[ \mathbf{e}_\alpha^\lambda\equiv \frac{\partial\,\mathbf{r}^\lambda}{\partial\, q_\alpha} \] であり(図3-7)、直交座標に分解すると \begin{eqnarray} \mathbf{e}_\alpha^1&=&\frac{\partial\, x_1}{\partial\, q_\alpha}\mathbf{e}_1+\frac{\partial\, x_2}{\partial\, q_\alpha}\mathbf{e}_2+\frac{\partial\, x_3}{\partial\, q_\alpha}\mathbf{e}_3\notag\\ \mathbf{e}_\alpha^2&=&\frac{\partial\, x_4}{\partial\, q_\alpha}\mathbf{e}_1+\frac{\partial\, x_5}{\partial\, q_\alpha}\mathbf{e}_2+\frac{\partial\, x_6}{\partial\, q_\alpha}\mathbf{e}_3\notag\\ \notag\\ &&\cdots\cdots\cdots\cdots\cdots\cdots\notag \end{eqnarray} である。 一方 \begin{eqnarray} m^1\ddot{\mathbf{r}}^1&=&m_1\ddot{x}_1\mathbf{e}_1+m_2\ddot{x}_2\mathbf{e}_2+m_3\ddot{x}_3\mathbf{e}_3\notag\\ m^2\ddot{\mathbf{r}}^2&=&m_4\ddot{x}_4\mathbf{e}_1+m_5\ddot{x}_5\mathbf{e}_2+m_6\ddot{x}_6\mathbf{e}_3\notag\\ \notag\\ &&\cdots\cdots\cdots\cdots\cdots\cdots\notag \end{eqnarray} である。だから \begin{equation} \sum_\lambda \mathbf{e}_\alpha^\lambda\cdot m^\lambda\ddot{\mathbf{r}}^\lambda=\sum_i\frac{\partial\, x_i}{\partial\, q_\alpha}m_i\ddot{x}_i \label{rre1} \end{equation} となる。これは1つ目の質点について\(m^1\mathbf{\ddot{r}}^1\)を\(\mathbf{e}_\alpha^1\)方向へ正射影して\(|\mathbf{e}_\alpha^1|\)倍し、2つ目の質点について\(m^2\mathbf{\ddot{r}}^2\)を\(\mathbf{e}_\alpha^2\)方向へ正射影して\(|\mathbf{e}_\alpha^2|\)倍し、・・・ということをすべての質点にして、それをすべて足し合わせたものが\(\sum_i\frac{\partial\, x_i}{\partial\, q_\alpha}m_i\ddot{x}_i\)になっているということである。
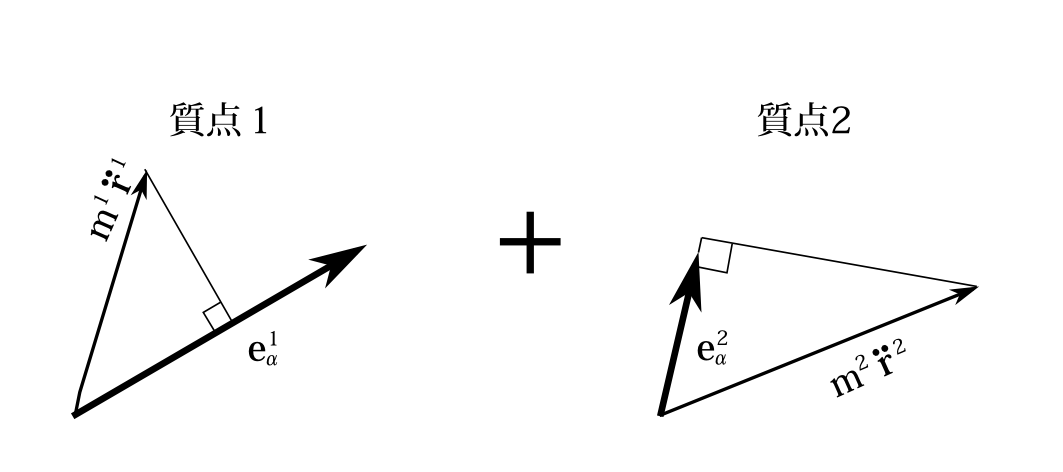
図3-8 \(m^1\mathbf{\ddot{r}}^1\)を\(\mathbf{e}_\alpha^1\)方向へ正射影して\(|\mathbf{e}_\alpha^1|\)倍、\(m^2\mathbf{\ddot{r}}^2\)を\(\mathbf{e}_\alpha^2\)方向へ正射影して\(|\mathbf{e}_\alpha^2|\)倍、・・・・をすべて合わせたものがラグランジュ方程式
同様に\(\mathbf{F}^1,\mathbf{F}^2,\mathbf{F}^3, \cdots\)をそれぞれ直交成分に分解すると \begin{eqnarray} \mathbf{F}^1&=&F_1\mathbf{e}_1+F_2\mathbf{e}_2+F_3\mathbf{e}_3\notag\\ \mathbf{F}^2&=&F_4\mathbf{e}_1+F_5\mathbf{e}_2+F_6\mathbf{e}_3\notag\\ \notag\\ &&\cdots\cdots\cdots\cdots\cdots\cdots\notag \end{eqnarray} であり \begin{equation} \sum_\lambda \mathbf{e}_\alpha^\lambda\cdot \mathbf{F}^\lambda= \sum_i\frac{\partial\, x_i}{\partial\, q_\alpha}F_i \label{fe1} \end{equation} となる。式(\ref{rre1})(\ref{fe1})からラグランジュ方程式は \[ \sum_\lambda \mathbf{e}_\alpha^\lambda\cdot m^\lambda\ddot{\mathbf{r}}^\lambda = \sum_\lambda \mathbf{e}_\alpha^\lambda\cdot \mathbf{F}^\lambda \] と表せる。だから一般に
定理3-2 ラグランジュ方程式の座標\(q_\alpha\)成分というのは、個々の粒子で\(m\ddot{\mathbf{r}}=\mathbf{F}\)という式を、その座標が増える方向に正射影して、その座標が1増えるときの長さ\(|\mathbf{e}_\alpha^\lambda|\)倍して、それをすべての粒子について足し合わせたものである。
と言える。だからどうということもないのだが、一応、直交座標を特別視せずにラグランジュ方程式の内容(注 内容と述べるのは、この式自体はラグランジュ方程式ではないが、ラグランジュ方程式は、この式の両辺を別の式に置き換えたものだからである)を書き下したことになるわけである。粒子が幾つかある場合は1粒子の場合のような幾何学的な簡単さはない。
3-4節 まとめ
ラグランジュ方程式は \[ \sum_\lambda \mathbf{e}_\alpha^\lambda\cdot m^\lambda\ddot{\mathbf{r}}^\lambda = \sum_\lambda \mathbf{e}_\alpha^\lambda\cdot \mathbf{F}^\lambda \] と表せる。ラグランジュ方程式の本質というのは、運動方程式の\(q_\alpha\)軸への正射影である。一般座標を使っての運動方程式であることがラグランジュ方程式の本質ではない。直交座標の\(m\ddot{x}_i=F_i\)を一般座標で表すことも可能なのである(注 例えば2-3節の式(16)のように)。そうではなくこの式に\(\frac{\partial\, x_i}{\partial\, q_\alpha}\)を掛けて\(q_\alpha\)軸に正射影することが本質である。