第8章 最小作用の原理
この章でも7章に引き続き、変分問題を扱う。いわゆる最小作用の原理というものである。ここでは1粒子の系に限定した最小作用の原理を扱う。7章での変分問題と異なり、今回の変分問題は空間の経路を色々変えて線積分\(\int_\alpha\sqrt{2m[E-V(\mathbf{r})]}\;ds\)の値を比較しようというのである。7章では時間の関数としての空間座標を色々変えた変分問題であった。同じ空間経路を通っても時間の関数としては異なることもあった。1次元なら空間経路は一つしか無いが時間の関数としてはいろいろある。この章で扱うのは空間経路を変えるので2次元以上でなければだめである。内容についてだが、まず作用積分というものを説明した。それから力学の法則を満たす軌道は、
停留軌道であるということを証明した。これは非常にわかりづらい証明である。力学の法則を満たす軌道は最小軌道になると考えられる。その証明はできないのだが、そう考える根拠を記した。
最小作用の原理を所要時間最小というものに結びつけた。これは少し無理矢理のようなところがある。これはフェルマの原理に似ているが、何か深い意味があるのかは不明である。まとめのところで多粒子系の最小作用の原理について簡単に言及した
作用積分
粒子は1つで、ポテンシャル\(V\)が与えられエネルギー\(E\)が保存する系を考える。空間軌道\(\alpha\)の
線積分
\[
\int_\alpha\sqrt{2m[E-V(\mathbf{r})]}\;ds
\]
を作用積分と呼ぼう。\(\int_\alpha\)は線積分の経路が軌道\(\alpha\)であるという意味。
\(E=\frac{p^2}{2m}+V\)なので、エネルギーと位置が与えられれば運動量の大きさが決まることになる。運動量の大きさが位置の関数という意味で\(p(\mathbf{r})\)と書こう。\(p(\mathbf{r})\)は
\[
p(\mathbf{r})=\sqrt{2m[E-V(\mathbf{r})]}
\]
である。だから作用積分は
\[
\int_\alpha p(\mathbf{r})ds
\]
とも書ける。
作用積分で想定される経路は何でもよい。もちろん力学の法則を満たす軌道でなくてよい。要はエネルギー保存の法則だけ満たしていればよい。
例題8-1
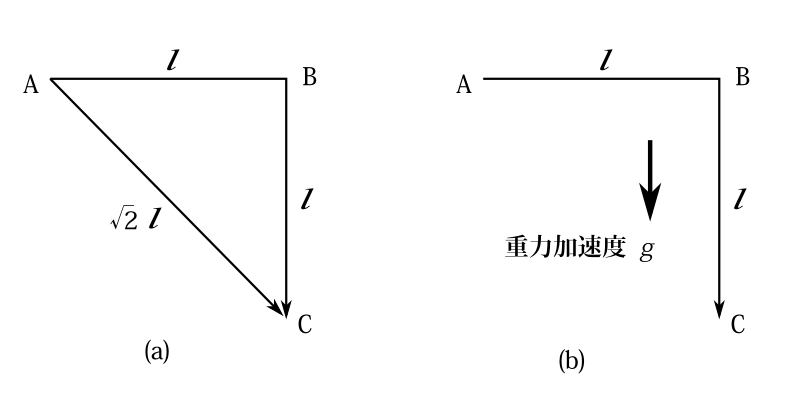
力が働いてない系で、エネルギー\(E\)
の粒子が図8-1(a)のようにAから直線を\(l\)進みBにつき、次に直角に曲がって\(l\)進んでCにつくという軌道の作用積分を求めよ。またAからCへまっすぐ進んだときの作用積分も求めよ。
【解】\(p=\sqrt{2mE}\)と一定でABC軌道の距離は\(2l\)なので作用積分は
\(2l\sqrt{2mE}\)である。又AC軌道の作用積分は\(\sqrt{2}\;l\sqrt{2mE}\)である。【解答終】
図8-1
例題8-2
図8-1(b)のように重力\(g\)があるときのABC軌道の作用積分を求めよ。点Aでの運動量を\(p_0\)とする。
【解】運動量を\(p_0\)とするとAB部分の作用積分は
\(p_0l\)である。一方BからCに向かって距離\(x\)進んだときの運動量\(p\)は、エネルギー保存の法則より\[\frac{p^2}{2m}=\frac{p_0^2}{2m}+mgx\]である。だから
\(p=\sqrt{p_0^2+2m^2gx}\)である。だからBC部分の作用積分は
\(\int_0^l\sqrt{p_0^2+2m^2gx}\;dx\)
である。だからABC軌道の作用積分は
\(p_0l+\int_0^l\sqrt{p_0^2+2m^2gx}\;dx\)である。【解答終】
変分
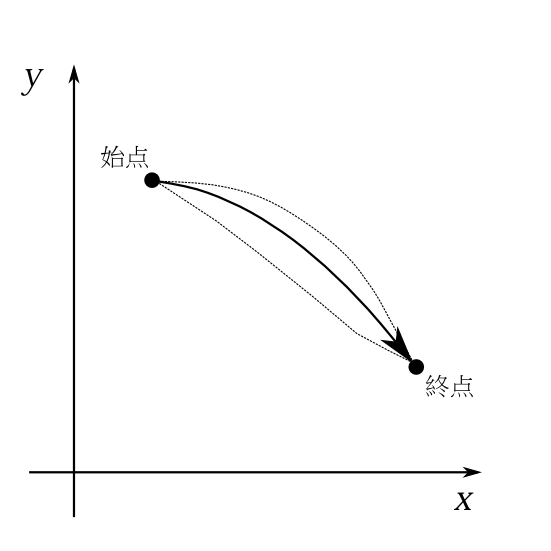
図8-2 始点と終点を固定して軌道を変化させ、
\(
\int_\alpha\sqrt{2m[E-V(\mathbf{r})]}\;ds
\)の値を比べる。
今から考える変分問題とは、軌道の始点と終点は同じで、エネルギーも同じである軌道
で
の作用積分の値を比較することである(図8-2)。作用積分
\(\int_\alpha\sqrt{2m(E-V(\mathbf{r}))}\;ds\)は軌道によって値が異なるので、軌道の関数である。それで、軌道の関数という意味で作用積分を
\[
I[\alpha]\equiv \int_\alpha\sqrt{2m(E-V(\mathbf{r}))}\;ds
\]
と書こう。
もしある軌道の作用積分が最小なら、その軌道を最小軌道と呼ぼう。もしある軌道をわずかに変化させたとき、作用積分の値が大きくなるなら、その軌道を極小軌道と呼ぼう。
もしある軌道をわずかに変化させても、変化の1次の範囲では、作用積分の値が変わらないとき、その軌道を停留軌道と呼ぼう。「わずかに変化」と言うのは意味が明瞭ではないが、わずかに変化させた軌道とは位置的に近く、かつ向きがほぼ平行な軌道と考えてもらいたい。
停留軌道のより詳細な定義は後で検討する
。最小軌道は定義から当然、極小軌道であり、停留軌道である。極小軌道は停留軌道である。
例題8-3
力の働いていない系では力学の法則を満たす軌道は最小軌道になることを示せ。
【解】\(V=0\)なので作用積分は\(\int_\alpha \sqrt{2mE}\;ds\)である。だから作用積分は\(\sqrt{2mE}\)に軌道の長さを掛けたものになる。\(E\)はどの軌道でも同じなので距離が一番短い軌道が最小軌道となる。始点と終点はどの軌道でも同じなので直線が最も短い。だから直線が最小軌道である。力学の法則を満たす軌道は直線である。よって力学の法則を満たす軌道は最小軌道である。【解答終】
図8-3
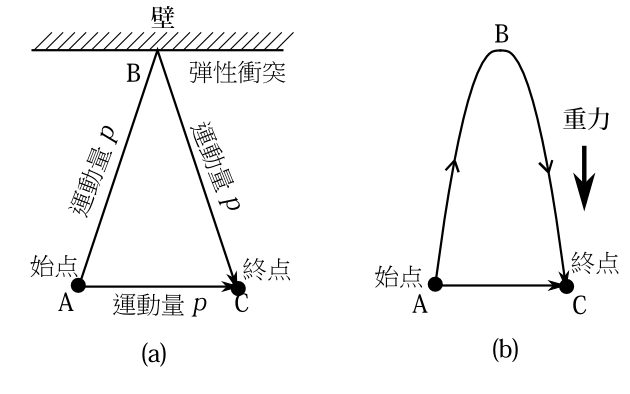
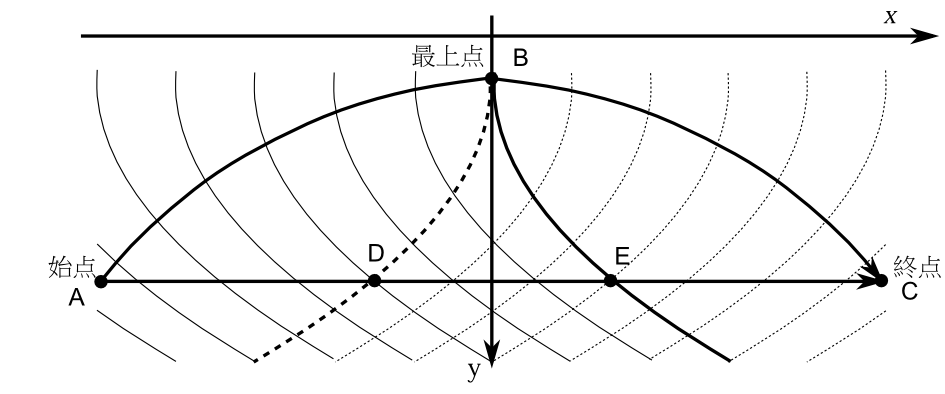
今の例題では力学の法則を満たす軌道は最小軌道になったが、力学の法則を満たす軌道すべてが最小軌道になるかというと、そうではない。図8-3(a)のように壁の所でしか力の働いていない系を考えよう。壁で弾性衝突するとしよう。AからBまで運動量が\(p\)で直線上に
進み、そこで強い力が働き、反射され運動量が\(p\)でCに戻ってくる軌道は力学の法則を満たす軌道である。一方直線ACを運動量\(p\)で通る軌道も力学の法則を満たす軌道である。そしてACの長さがABより短ければ、作用積分は明らかにAC軌道の方が小さい。
もう1つ例を見よう。図8-3(b)のように地球上でボールを点Aから初期運動量\(p\)で斜め上に投げ、最上点Bに達し、同じ高さの点Cに戻ってくるという軌道を考えよう。これは力学の法則を満たす軌道である。また直線ACを運動量\(p\)で進む軌道を考えよう。これは力学の法則を満たさない軌道である。ABに比してACの距離が十分短ければ作用積分は直線AC軌道の方が小さくなる。だから力学の法則を満たす軌道は最小軌道になっていない。今の2つの例は一種の反射のある場合である。反射のない場合は力学の法則を満たす軌道は最小軌道になると思う。その根拠は8-5節で説明する。
停留性については、反射のある場合も含めて以下のことが成り立つ。
定理8-1
力学の法則を満たす軌道は停留軌道である。
通常この数学的事実のことを最小作用の原理という。証明は正直言って、煩雑でわかりづらいく、そして何と言ってもつまらない。飛ばしてもらっていい。
(証明の準備)
証明のための補題を証明する。
粒子が始点を出発してから終点に到着するまでにかかる時間は軌道ごとに異なる。それでその時間が軌道\(\alpha\)の関数という意味で\(t(\alpha)\)と書こう。又始点を出発してからの時間\(t\)を決めれば位置が決まる。その時間依存性も軌道によって異なる。軌道\(\alpha\)と時間\(t\)の関数という意味で、それを\(\mathbf{r^\alpha}(t)\)と書こう。積分変数を距離の\(ds\)から時間\(dt\)に変えよう。
\[
ds=v dt
\]
なので
\[
\int_\alpha p(\mathbf{r})ds=\int_0^{t(\alpha)}p[\mathbf{r^\alpha}(t)]\cdot \frac{p[\mathbf{r^\alpha}(t)]}{m}\;dt
\]
が成り立つ。\(p^2/m\)は運動エネルギー\(T\)の2倍である。だから
\[
\int_\alpha p(\mathbf{r})ds=\int_0^{t(\alpha)}2T[\mathbf{r^\alpha}(t)]\;dt
\]
が成り立つ。\(2T=(T-V)+(T+V)=L+E\)なので(\(L\)はラグランジアン)、作用積分は
\[
\int_\alpha p(\mathbf{r})ds
=\int_0^{t(\alpha)}\Big(L\left[\mathbf{{r}^\alpha}(t),\mathbf{\dot{r}^\alpha}(t)\right]+E\Big)\;dt
\]
とも書ける
(注
今は直交座標で、ポテンシャルも時間を含まないので、ラグランジアンも時間を含まない。
)
。だから
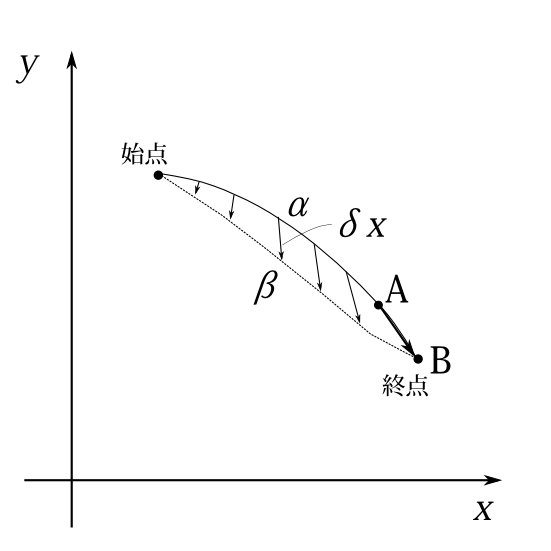
図8-4 \(\beta\)軌道が終点Bに着いたときの\(\alpha\)軌道の位置がA。\(\delta x\)は同一時刻での2つの軌道の差
2つの軌道\(\alpha\)と\(\beta\)の作用積分の差\(I[\alpha]-I[\beta]\)を考えよう。この2つの軌道は十分接近しているとする。始点を同時に出発し、\(\beta\)軌道の方が先に終点に着くとしよう。すなわち
\[
t(\beta) < t(\alpha)
\]
とする。\(\alpha\)軌道の作用積分の時間を\(0\)から\(t(\beta)\)と\(t(\beta)\)から\(t(\alpha)\)に分割しよう。すなわち
\[
I[\alpha]=\int_0^{t(\beta)}\Big(L\left[\mathbf{{r}^\alpha}(t),\mathbf{\dot{r}^\alpha}(t)\right]+E\Big)\;dt
+
\int_{t(\beta)}^{t(\alpha)}\Big(L\left[\mathbf{\dot{r}^\alpha}(t),\mathbf{r^\alpha}(t)\right]+E\Big)\;dt
\]
とする。
\(\alpha\)軌道のうち、時間\(t(\beta)\)から\(t(\alpha)\)の間に動く部分を\(\Delta \alpha\)と書こう。すると
\[
\int_{t(\beta)}^{t(\alpha)}\Big(L\left[\mathbf{{r}^\alpha}(t),\mathbf{\dot{r}^\alpha}(t)\right]+E\Big)\;dt
=\int_{\Delta\alpha}p(\mathbf{r})ds
\]
である。だから
\[
I[\alpha]=\int_0^{t(\beta)}\Big(L\left[\mathbf{{r}^\alpha}(t),\mathbf{\dot{r}^\alpha}(t)\right]+E\Big)\;dt
+
\int_{\Delta\alpha}p(\mathbf{r})ds
\]
となる。\(E\)は2つの軌道で等しいので
\begin{equation}
I[\beta]-I[\alpha]=
\int_0^{t(\beta)}\Big(L\left[\mathbf{{r}^\beta}(t),\mathbf{\dot{r}^\beta}(t)\right]-
L\left[\mathbf{{r}^\alpha}(t),\mathbf{\dot{r}^\alpha}(t)\right]\Big)
\; dt-
\int_{\Delta\alpha}p(\mathbf{r})ds
\label{gan1}
\end{equation}
となる。
ベクトル\(\mathbf{r^\beta}(t)-\mathbf{{r}^\alpha}(t)\)の\(i\)成分を\(\delta x_i(t)\)と書こう。
\(L\left[\mathbf{{r}^\alpha}(t),\mathbf{\dot{r}^\alpha}(t)\right]\)を短く\(L^\alpha(t)\)と書こう。
\(\alpha\)軌道で展開
\(\delta x_i,\delta \dot{x}_i\)の1次の範囲で
\[
\int_0^{t(\beta)}L^\beta(t)-L^\alpha(t)\; dt
\cong\int_0^{t(\beta)}\sum_{i=1}^3 \left[\frac{\partial\, L_\alpha(t)}{\partial\, x_i}\delta x_i+\frac{\partial\, L_\alpha(t)}{\partial\, \dot{x}_i}\delta \dot{x}_i \right]dt
\]
である。\(\displaystyle \frac{\partial\, L_\alpha}{\partial\, \dot{x}_i}\delta \dot{x}_i\)を部分積分すると、これは
\[
\int_0^{t(\beta)}\sum_{i=1}^3 \left[\frac{\partial\, L_\alpha(t)}{\partial\, x_i}-\frac{d}{dt}\left(\frac{\partial\, L_\alpha(t)}{\partial\, \dot{x}_i}\right) \right]\delta x_i\;dt
+
\sum_{i=1}^3\frac{\partial\, L_\alpha[t(\beta)]}{\partial\, \dot{x}_i}\delta x_i[t(\beta)]-\sum_{i=1}^3\frac{\partial\, L_\alpha(0)}{\partial\, \dot{x}_i}\delta x_i[0]
\]
となる。
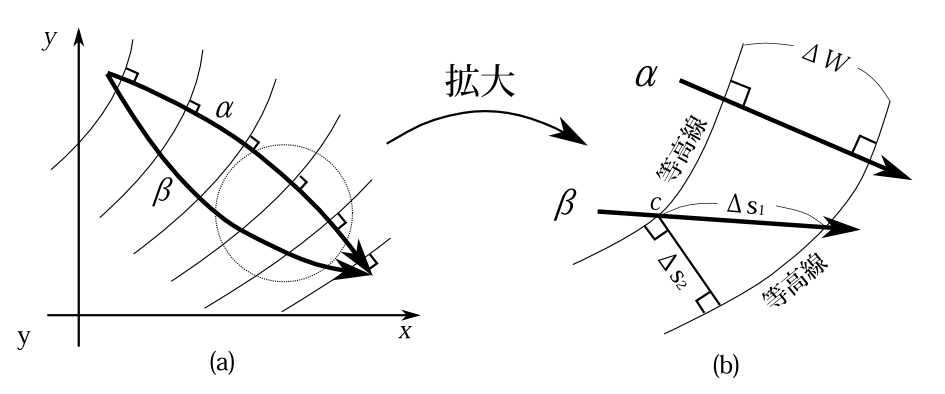
時間が\(t(\beta)\)のときの\(\alpha\)軌道、\(\beta\)軌道の位置をそれぞれA,Bとしよう(図8-4)。点Bは軌道の終点である。第2項の\(\delta x_i[t(\beta)]\)は、ベクトル\(\overrightarrow{\text{AB}}\)の\(i\)成分である。点Aでの\(\alpha\)軌道の運動量ベクトルを\(\mathbf{p^\alpha}(\text{A})\)と書くと、第2項は
\[
\mathbf{p^\alpha}(\text{A})\cdot \overrightarrow{\text{AB}}
\]
と書ける。第3項だが、2つの軌道は同時に出発しているので\(\delta x_i(0)=0\)である。だから第3項は0である。だから
\begin{equation}
I[\beta]-I[\alpha]\cong
\int_0^{t(\beta)}\sum_{i=1}^3 \left[\frac{\partial\, L_\alpha(t)}{\partial\, x_i}-\frac{d}{dt}\left(\frac{\partial\, L_\alpha(t)}{\partial\, \dot{x}_i}\right) \right]\delta x_i\;dt+
\mathbf{p^\alpha}(\text{A})\cdot \overrightarrow{\text{AB}} -
\int_{\Delta\alpha}p(\mathbf{r})ds
\label{tyokusen}
\end{equation}
となる。点Aでの運動量大きさを\(p(\text{A})\)と書こう。直線ABの長さを\(\overline{\text{AB}}\)と書こう。
もし2つの軌道が十分接近していて、その結果BとAが十分接近しいるとしてよく、その結果
A1. 点Aでの\(\alpha\)軌道の進む向きが、ベクトル\(\overrightarrow{\text{AB}}\)の向きに等しいとしてよいなら
\begin{equation}
\mathbf{p^\alpha}(\text{A})\cdot \overrightarrow{\text{AB}}\cong
p(\text{A})\,\overline{\text{AB}}
\label{sa11}
\end{equation}
と近似できる。
一方\(\int_{\Delta\alpha}p(\mathbf{r})ds\)は
、もし2つの軌道が十分接近していて、その結果BとAが十分接近しいるとしてよく、その結果
A2. AからBへの軌道上で運動量の大きさは常にAでの運動量の大きさとしてよく、かつAからBまでの軌道を直線とみなしてよいなら
\begin{equation}
\int_{\Delta\alpha}p(\mathbf{r})ds
\cong
p(\text{A})\overline{\text{AB}}
\label{sa12}
\end{equation}
と近似できる。式(\ref{sa11})、式(\ref{sa12})から、式(\ref{tyokusen})の第2項と第3項はキャンセルする。よって
\begin{equation}
I[\beta]-I[\alpha]\cong
\int_0^{t(\beta)}\sum_{i=1}^3 \left[\frac{\partial\, L_\alpha(t)}{\partial\, x_i}-\frac{d}{dt}\left(\frac{\partial\, L_\alpha(t)}{\partial\, \dot{x}_i}\right) \right]\delta x_i\;dt
\label{sa13}
\end{equation}
となる。
もし\(\alpha\)軌道が力学の法則を満たす軌道なら\(I[\beta]-I[\alpha]\cong 0\)である。
今示したことは力学の法則を満たす軌道の作用積分とその軌道より先に終点に着く軌道の作用積分との差は2つの軌道が十分接近していれば\(\delta x_i(t),\delta \dot{x}_i\)の1次の範囲では0であるということである。だから力学の法則を満たす軌道より後に終点に着く軌道の作用積分との差が\(0\)となることも示さなければならない。
\(\beta\)軌道で展開)
その方法は2つあるのだが、まず今のと同じ方法のものから書こう。
式(\ref{gan1})をもう一度書くと
\[
I[\beta]-I[\alpha]=
\int_0^{t(\beta)}L\left[\mathbf{{r}^\beta}(t),\mathbf{\dot{r}^\beta}(t)\right]-
L\left[\mathbf{{r}^\alpha}(t),\mathbf{\dot{r}^\alpha}(t)\right]
\; dt-
\int_{\Delta\alpha}p(\mathbf{r})ds
\]
である。ここでの
\(L^\beta(t)-L^\alpha(t)\)を前回は\(\alpha\)軌道を基準に展開したが、今回は\(\beta\)軌道を基準に展開しよう。
ベクトル\(\mathbf{r^\alpha}(t)-\mathbf{r^\beta}(t)\)の各成分は\((-\delta x_i)\)なので、\(L^\beta(t)-L^\alpha(t)\)は\(\delta x_i,\delta \dot{x}_i\)の1次の範囲で
\begin{eqnarray}
\int_0^{t(\beta)}L^\beta(t)-L^\alpha(t)\; dt&=&-\int_0^{t(\beta)}
L^\alpha(t)-L^\beta(t)\; dt\notag\\
&=&
-\int_0^{t(\beta)}\sum_{i=1}^3 \left[\frac{\partial\, L_\beta(t)}{\partial\, x_i}(-\delta x_i)+\frac{\partial\, L_\beta(t)}{\partial\, \dot{x}_i}(-\delta \dot{x}_i) \right]dt\notag\\
&=&
\int_0^{t(\beta)}\sum_{i=1}^3 \left[\frac{\partial\, L_\beta(t)}{\partial\, x_i}(\delta x_i)+\frac{\partial\, L_\beta(t)}{\partial\, \dot{x}_i}(\delta \dot{x}_i) \right]dt\notag
\label{gan2c}
\end{eqnarray}
となる。そして前回と同じように\(\displaystyle \frac{\partial\, L_\beta}{\partial\, \dot{x}_i}\delta \dot{x}_i\)を部分積分すると
\[
\int_0^{t(\beta)}\sum_{i=1}^3 \left[\frac{\partial\, L_\beta(t)}{\partial\, x_i}-\frac{d}{dt}\left(\frac{\partial\, L_\beta(t)}{\partial\, \dot{x}_i}\right) \right]\delta x_i\;dt
+
\sum_{i=1}^3\frac{\partial\, L_\beta[t(\beta)]}{\partial\, \dot{x}_i}\delta x_i[t(\beta)]-\sum_{i=1}^3\frac{\partial\, L_\beta(0)}{\partial\, \dot{x}_i}\delta x_i(0)
\]
となる。
前回と違うのは\(L_\alpha\)が\(L_\beta\)になっているだけである。
\(\beta\)軌道の点Bでの運動量ベクトルを\(\mathbf{p^\beta}(\text{B})\)と書こう。すると第2項は
\[
\mathbf{p^\beta}(\text{B})\cdot \overrightarrow{\text{AB}}
\]
となる。
前回は\(\mathbf{p^\alpha}(A)\)だったのが\(\mathbf{p^\beta}(B)\)に変わった。
第3項は\(\delta x_i(0)=0\)なので0である。だから
\begin{equation}
I[\beta]-I[\alpha]\cong
\int_0^{t(\beta)}\sum_{i=1}^3 \left[\frac{\partial\, L_\beta(t)}{\partial\, x_i}-\frac{d}{dt}\left(\frac{\partial\, L_\beta(t)}{\partial\, \dot{x}_i}\right) \right]\delta x_i\;dt+
\mathbf{p^\beta}(\text{B})\cdot \overrightarrow{\text{AB}} -
\int_{\Delta\alpha}p(\mathbf{r})ds
\label{dake}
\end{equation}
となる。
もし2つの軌道が十分接近していて、その結果BとAが十分接近しいるとしてよく、その結果
B1. 点Bでの\(\beta\)軌道の進む向きが、\(\overrightarrow{\text{AB}}\)の向きに等しいとしてよいなら
\begin{equation}
\mathbf{p^\beta}(\text{B})\cdot \overrightarrow{\text{AB}}\cong
p(\text{B})\overline{\text{AB}}
\label{sa11c}
\end{equation}
と近似できる。\(p(\text{B})\)というのは点Bでの運動量の大きさ。一方\(\int_{\Delta\alpha}p(\mathbf{r})ds\)は
、もし2つの軌道が十分接近していて、その結果BとAが十分接近しいるとしてよく、その結果
B2. AからBへの軌道上で運動量の大きさは常にBでの運動量の大きさとしてよく、かつAからBまでの軌道を直線とみなしてよいなら
\begin{equation}
\int_{\Delta\alpha}p(\mathbf{r})ds
\cong
p(\text{B})\overline{\text{AB}}
\label{sa12c}
\end{equation}
と近似できる。式(\ref{sa11c})、式(\ref{sa12c})から、式(\ref{dake})の第2項と第3項はキャンセルする。よって
\begin{equation}
I[\beta]-I[\alpha]\cong
\int_0^{t(\beta)}\sum_{i=1}^3 \left[\frac{\partial\, L_\beta(t)}{\partial\, x_i}-\frac{d}{dt}\left(\frac{\partial\, L_\beta(t)}{\partial\, \dot{x}_i}\right) \right]\delta x_i\;dt
\label{sa13c}
\end{equation}
となる。もし\(\beta\)軌道が力学の法則を満たす軌道なら\(I[\beta]-I[\alpha]\cong 0\)である。
だからもし\(\beta\)軌道、すなわち先に終点に着く軌道が力学の法則を満たしているならば、その軌道の作用積分と後に着く軌道の作用積分の差は\(\delta x,\delta \dot{x}\)の1次の範囲では0となるわけである。以上から、力学の法則を満たす軌道は停留軌道になるというわけである。
今は軌道がラグランジュ方程式を満たしているなら、作用積分の停留軌道になるということを証明したのだが、その逆
のすべての停留軌道はラグランジュ方程式を満たすかということについては何とも言えない。式(\ref{sa13})、(\ref{sa13c})の右辺
\[
\int_0^{t(\beta)}\sum_{i=1}^3 \left[\frac{\partial\, L_\alpha(t)}{\partial\, x_i}-\frac{d}{dt}\left(\frac{\partial\, L_\alpha(t)}{\partial\, \dot{x}_i}\right) \right]\delta x_i\;dt
\]
での\(\delta x_i\)は、第7章での変分のときと違い、\(E=\)一定という制限があるので任意ではない。だから、ラグランジュ方程式を満たさなくてもこの積分が0になるかもしれないからである。
(別証)
もう1つの証明法を書こう。今は汎軌道の変分は\(\delta x,\delta\dot{x}\)の1次の範囲で
\begin{equation}
I[\beta]-I[\alpha]\cong
\int_0^{t(\beta)}\sum_{i=1}^3 \left[\frac{\partial\, L_\alpha(t)}{\partial\, x_i}-\frac{d}{dt}\left(\frac{\partial\, L_\alpha(t)}{\partial\, \dot{x}_i}\right) \right]\delta x_i\;dt
\label{mat}
\end{equation}
と近似できかつ
\begin{equation}
I[\beta]-I[\alpha]\cong
\int_0^{t(\beta)}\sum_{i=1}^3 \left[\frac{\partial\, L_\beta(t)}{\partial\, x_i}-\frac{d}{dt}\left(\frac{\partial\, L_\beta(t)}{\partial\, \dot{x}_i}\right) \right]\delta x_i\;dt
\label{mat2}
\end{equation}
とも近似できるということをわざわざ示したわけである。軌道が近ければ、同時刻での\(\frac{\partial\, L}{\partial\, x_i}-\frac{d}{dt}\left(\frac{\partial\, L}{\partial\, \dot{x}_i}\right)\)の値も近いであろう。だから式(\ref{mat})が成り立つなら式(\ref{mat2})が成り立つと言えそうである。
\(\frac{\partial\, L}{\partial\, x_i}-\frac{d}{dt}\left(\frac{\partial\, L}{\partial\, \dot{x}_i}\right)\)というのは、それぞれ
\[
\frac{\partial\, L_\alpha}{\partial\, x_i}-\frac{d}{dt}\left(\frac{\partial\, L_\alpha}{\partial\, \dot{x}_i}\right)
=
F_i(\mathbf{r^\alpha})-m{\ddot{x}^\alpha_i}
\qquad\qquad
\frac{\partial\, L_\beta(t)}{\partial\, x_i}-\frac{d}{dt}\left(\frac{\partial\, L_\beta(t)}{\partial\, \dot{x}_i}\right)=
F_i(\mathbf{r^\beta})-m{\ddot{x}^\beta_i}
\]
である。ここで\(F_i\)は位置によって決まる力。前の記号で\(x^\alpha_i-x^\beta_i=(-\delta x_i)\)である。\((-\delta x_i)\)の1次の範囲で
\[
F_i(\mathbf{r^\alpha})-m{\ddot{x}^\alpha_i}\cong
F_i(\mathbf{r^\beta})-m{\ddot{x}^\beta_i}
+
\Big[
\sum_j\frac{\partial\,}{\partial\, x_j}F_i(\mathbf{r^\beta})(-\delta x_j)
-m(-\delta \ddot{x}_i)
\Big]
\]
である。
これを式(\ref{mat})に代入すると、
\begin{eqnarray}
I[\beta]-I[\alpha]\cong
\int_0^{t(\beta)}&\sum_{i=1}^3& \left[\frac{\partial\, L_\beta(t)}{\partial\, x_i}-\frac{d}{dt}\left(\frac{\partial\, L_\beta(t)}{\partial\, \dot{x}_i}\right) \right]\delta x_i\;dt\notag\\
&+&
\int_0^{t(\beta)}\sum_{i=1}^3 \Big[-
\sum_j\frac{\partial\,}{\partial\, x_j}F_i(\mathbf{r^\beta})\delta x_j
+m\delta \ddot{x}_i
\Big]\delta x_i \; dt
\label{keseru}
\end{eqnarray}
となる。ところで部分積分法を使うと
\[
\int_0^{t(\beta)}
\delta \ddot{x}_i\delta x_i dt
=[\delta \dot{x}\delta x_i] ^{t(\beta)}_0
-
\int_0^{t(\beta)}\delta \dot{x}_i\delta \dot{x}_i\; dt
\]
となる。だから式(\ref{keseru})の第2項にある\(\delta \ddot{x}\)の項は消せる。だから第2項は\(\delta x_i^2,\delta\dot{x}_i^2,\delta \dot{x}\delta x_i\)のオーダーとなる。だから式(\ref{mat})が成り立つなら
\(\delta x_i,\delta\dot{x}_i\)の1次の範囲で
式(\ref{mat2})が成り立つと言える。
別証の考え方はわかりやすいが、面倒でややこしいことには変わりがない。
今の証明は、いろいろと時間やら運動量やら、エネルギーやらでてきて実にややこしかったが、そういう物理量という概念を忘れて単に数学として考えた方がすっきりと本質が見えるかもしれない。
定理8-1の主張していることは、数学的には以下のことである。
与えられた数\(E\)、与えられた位置の関数\(V\)があるとき線積分
\[
\int_\alpha\sqrt{2m[E-V(\mathbf{r})]}\;ds
\]
が停留する軌道は何か。その答えというのは、まず
\[
dt=\frac{m}{\sqrt{2m[E-V(\mathbf{r})]}}\;ds
\]
という距離\(ds\)と異なるパラメータ\(t\)を導入する。\(t\)を時間だとか考えず、上の式に定義したただの積分変数と考える。与えられた軌道の位置を\(x_i(t)\)というように\(t\)の関数で表す。そしてその軌道がもし
\[
m\frac{d^2x_i}{dt^2}=-\frac{\partial\, V}{\partial\, x_i}
\]
を満たしているなら、その軌道は停留軌道になるということなのである。
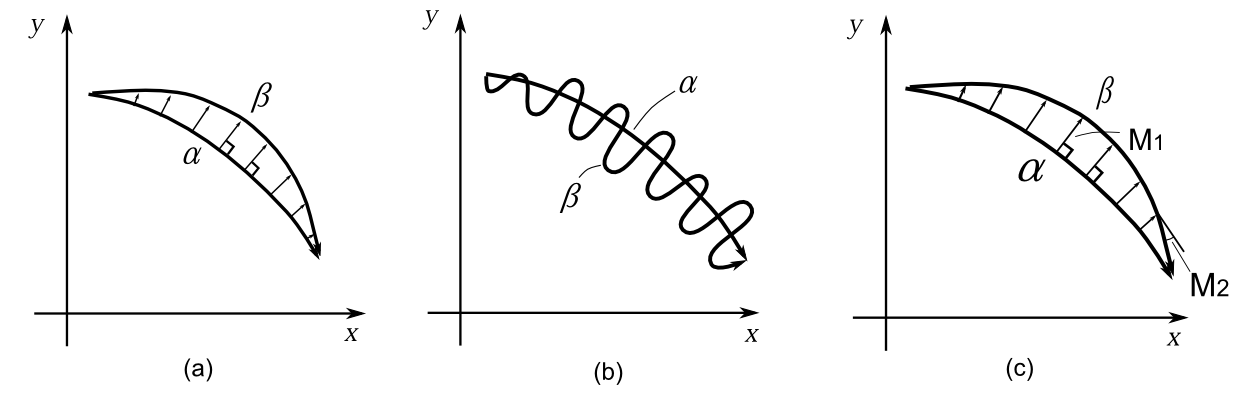
最初に停留軌道というのは軌道をわずかに変化させても、その作用積分が変化しない軌道だと述べた。それでは意味が少しあいまいなので、より厳密な言葉に置き換えたい。力学の法則を満たす軌道を\(\alpha\)、満たさない軌道を\(\beta\)軌道とする。\(\alpha\)軌道と\(\beta\)軌道との差ということだが、例えば、図8-5(a)のように\(\alpha\)軌道から直角に\(\beta\)軌道に線を引き、その長さと考えるのがよいだろう。
図8-5 (a):わずかに変化させた軌道というためには幅が狭く無くてはならない。(b):向きが大きく異なっていてはわずかに変化させたとは言えない。(c):幅の最大値が\(M_1\)角度差の最大値が\(M_2\)。
その長さの最大値が0に近づくとき、作用積分の差はそれより速く0に近づくというのが停留軌道であろう。しかし図8-5(b)のように、いくら幅を狭くしても、軌道の向きが全く異なるようでは、軌道をわずかに変化させたとは言えないであろう。
それに軌道が長くなると、作用積分も大きくなってしまう。
以上の考察から停留軌道の定義を以下のようにすればよいと思う。
\(\alpha\)軌道上の点から\(\alpha\)軌道に対して直角の線を引き、それが\(\beta\)軌道に当たるまでの長さがある。\(\alpha\)軌道のいろいろな点からの長さを測り、その最大値を\(M_1\)としよう(図8-5(c)参)。そして、その幅を測った線と\(\beta\)軌道との角度がある。それの90°との差の最大値を\(M_2\)としよう。\(M_1,M_2\)の大きい方を\(M_3\)としよう。今\(\alpha\)軌道を固定して、\(\beta\)軌道を変化させて、\(M_3\to 0\)となるようにしよう。そのとき任意の\(\beta\)軌道に対して
\[
\lim_{M_3\to 0}\frac{I[\beta]-I[\alpha]}{M_3}=0
\]
となるなら、\(\alpha\)軌道は停留軌道であるというのが停留軌道の定義でよいだろう。少し長くなってしまったが意味はわかったと思う。
さて、このように停留軌道を定義して、力学の法則を満たす軌道は停留軌道になるのだろうか。それにはもう一度、先の証明を検証してみる必要がある。仮定として使ったのはA.1、A.2、B.1、B.2である。だからそれが今の定義で成り立つかを検証すれば良い。ただそれは何か技術的で煩雑な作業に思えるので、そのことについては調べていない。私自身はこの定義でも停留軌道になると思っている。
力学の法則を満たす反射のない軌道は最小軌道になるであろうと述べたが、その根拠を書こう。力学の法則を満たす軌道があり、それはあるハミルトンヤコビの方程式の解から導かれたとする。すなわち
\[
\frac{\partial\, S}{\partial\, x_i}=p_i
\qquad\qquad
\frac{\partial\, S}{\partial\, \alpha_i}=\beta_i
\]
から\(x,p\)を\(\alpha,\beta,t\)の関数として求めて\(\alpha,\beta\)を適当に定めればその軌道になるということである。それで\(\alpha\)は定められたので\(S\)は\(x,t\)のみの関数となる。
1つの力学軌道に対して、必ずそれに対応するハミルトンヤコビの方程式の解があるかどうかは証明していないが、あると思う。
時間を含まないハミルトンヤコビの方程式は
\[
\frac{|\nabla W|^2}{2m}+V=E
\]
なので、
\[
\sqrt{2m(E-V)}=|\nabla W|
\]
である。だから作用積分\(I[\alpha]\)は
\[
I[\alpha]=\int_\alpha |\nabla W|\;ds
\]
と書ける。
微小距離\(ds\)に対応する微小変位ベクトルを\(\mathbf{ds}\)と書こう。力学の法則を満たす軌道では\(\mathbf{p}=\nabla W\)なので、\(\mathbf{ds}\)はベクトル\(\nabla W\)の向きに等しい。だから
\[
|\nabla W|\;ds=\nabla W\cdot \mathbf{d s}
\]
が成り立つ。だから
\[
I[\alpha]=\int_\alpha|\nabla W|ds=\int_\alpha \frac{\partial\, W}{\partial\, x}dx+\frac{\partial\, W}{\partial\, y}dy+\frac{\partial\, W}{\partial\, z}dz
\]
となる。だから
補題8-2
力学の法則を満たす軌道の作用積分はその軌道に対応するハミルトンヤコビの方程式の時間を含まない解\(W\)の始点から終点までの増加量である。
と言える。
では力学の法則を満たさない軌道の作用積分はどうなるか。図8-6(a)のように始点から終点まで\(W\)の等高線をその区間で軌道が直線とみなせるくらい十分細かく間隔でひこう。
図8-6
(a):力学の法則を満たす軌道\(\alpha\)は等高線に直交するが、そうでない軌道\(\beta\)は直交しない部分がある。(b):その拡大図。\(|\nabla W|\Delta s_1\le \Delta W\)となる。
\(\alpha\)を力学の法則を満たす軌道とする。\(\beta\)を力学の法則を満たさない軌道とする。
\(\alpha\)は常に等高線に直交するが、\(\beta\)には必ず等高線と直交しない箇所がある。というのは常に直交していたら、それは\(\alpha\)と同じになってしまうからである。その直交しない区間をとりだして拡大すると図8-6(b)のようになる。その区間での等高線間の作用積分の値を比較しよう。
その等高線間の\(W\)の差を\(\Delta W\)としよう。\(\alpha\)軌道ではその区間での作用積分の値は補題8-2より、\(\Delta W\)となる。
\(\beta\)軌道が等高線と交わる点を\(c\)とし(図8-6(b))、又、\(\beta\)軌道のこの2つの等高線間の距離を\(\Delta s_1\)とする。するとこの2つの等高線間の\(\beta\)軌道の作用積分は
\[
\sqrt{2m[E-V(c)]}\Delta s_1=
|\nabla W(c)|\Delta s_1
\]
となる。
同じ\(c\)を通って等高線に直交する線を考え、\(\Delta s_2\)をその等高線間の距離とする。\(\Delta s_2\)は\(\Delta s_1\)より短いので
\[
|\nabla W(c)|\Delta s_1>|\nabla W(c)|\Delta s_2
\]
が成り立つ。ところで\(\Delta s_2\)の向きは等高線に直交しているので\(\nabla W\)の向きに等しい。だから補題8-2を導いたのと同じ理由で、\(|\nabla W(c)|\Delta s_2\)は\(\Delta W\)に等しい。だから
\(\beta\)軌道のこの区間での作用積分は同じ等高線区間での\(\alpha\)軌道の作用積分より大きい。\(\beta\)軌道は等高線と直交している区間では、その部分の\(\alpha\)の作用積分と等しく、直交していない区間では、それよりも大きい。だから全体としては必ず大きくなる。力学の法則を満たす軌道が横切る等高線の数と同じ数だけ横切っている力学の法則を満たさない軌道の作用積分は力学の法則を満たす軌道のそれより必ず大きくなるということを示したわけである。もっと簡単に言えば\(W\)の連続な領域内にある軌道の中では最小ということである。すなわち
定理8-2
力学の法則を満たす軌道に対応する\(W\)が存在し、その\(W\)の定義域内に入っている軌道の中では、力学の法則を満たす軌道が最小である。
といえる。
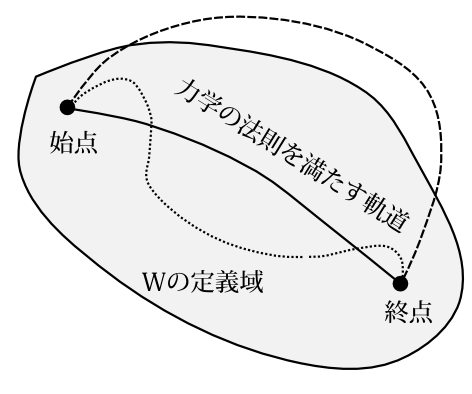
だから図8-7のように
1. 力学の法則を満たす軌道を包み込むような\(W\)が存在すればその軌道は極小軌道であり、
2. その\(W\)の定義域が作用積分で許される定義域をすべて包み込んでいるなら、その軌道は最小軌道である
と言えるわけである。この主張を具体例で見てみよう。
図8-7
グレイの部分が力学の法則を満たす軌道に対応する\(W\)の定義域。その定義域に入っている軌道の作用積分は力学の法則を満たす軌道の作用積分より大きい。その領域外を通る軌道については何とも言えない。
2次元自由粒子
2次元自由粒子を考えよう。この場合ハミルトンヤコビの方程式の解は
\[
S=-\frac{\alpha_x^2+\alpha_y^2}{2m}t+\alpha_xx+\alpha_yy
\]
である。この\(S\)から\(\alpha,\beta\)を適当に選べばどんな力学の法則を満たす軌道も表せる。そして
\[
W=\alpha_xx+\alpha_yy
\]
は\(x,y\)の全領域を覆っている。だから自由粒子での力学の法則を満たす軌道は最小軌道になる。これはこの章の始めにも述べたことだが、新たに証明し直したわけである。
2次元自由落下
2次元自由粒子を考えよう。6-7節で見たように\(y\)軸の正の向きを重力の向きにとったときの、\(W\)は
\[
W=p_x x+\int^y\sqrt{2m\left(E-\frac{p_x^2}{2m}+mgy'\right)}\;dy'
\]
であった
(注 これに
\[
E=E_y+\frac{p_x^2}{2m}
\qquad\qquad
p_x=\alpha_x
\]
を代入して積分すれば6章の式(20)になる。
)
。この\(W\)の定義域は\(y\)が\(E-\frac{p_x^2}{2m}+mgy\ge 0\)、すなわち
\[
y\ge\frac{1}{mg}\left(\frac{p_x^2}{2m}-E\right)
\]
を満たす領域である。
一方、作用積分で軌道の通ることができる領域というのは
\(E-V\ge 0\)が満たされる領域である。今の場合で言えば\(y\)が\(E+mgy\ge 0\)、すなわち
\[
y\ge\frac{1}{mg}\left(-E\right)
\]
を満たす領域である。だから作用積分で軌道が通ることが許される領域の方が、Wの定義域より広いのである。
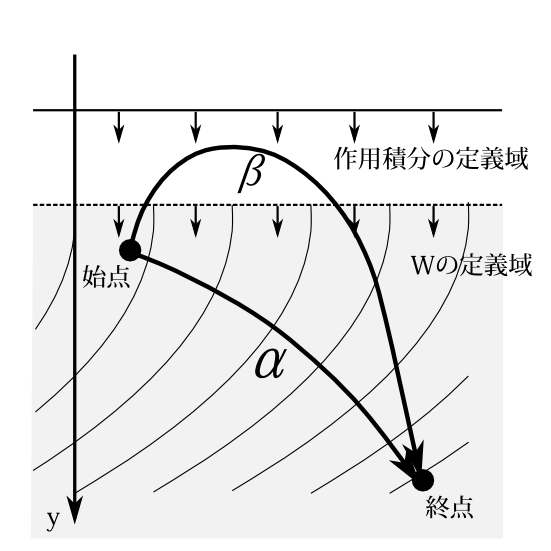
だから\(W\)の定義域を超えた図8-8の\(\beta\)のような軌道も作用積分の経路として考えることができる。
図8-8 \(W\)の定義域外を通る軌道に対しては、今の論法は使えない。実線より下が作用積分の定義域。破線より下が\(W\)の定義域。作用積分の定義域の方が広い。
今の論法では、そのような軌道の作用積分は、力学の法則を満たす軌道のそれより小さいとは断定できないのである。
しかしながら
\[
\int_\alpha p(\mathbf{r})ds
\]
という積分は運動量の大きさが小さく、距離が短い方が値は小さくなり、そのバランスで、それを最も小さくする軌道が定まるのである。例えば一様重力場の場合なのだが、図8-8の\(\alpha\)という軌道を徐々に上にずらしていき、図8-8の\(\beta\)軌道に持っていく。その軌道がすべて\(W\)の定義域に入っているときは作用積分は\(\alpha\)軌道より大きいのである。それが\(W\)
の定義域を超えたからと言って、急に作用積分が小さくなるというのは想像しにくいところである。だからおそらく力学の法則を満たす軌道は最小軌道になっているのであろう。
反射がある場合
図8-9 軌道のAB部分に対応するのは直線AE。軌道BCに対応するのは直線DC
次に一様重力場で反射がある場合を考えよう。
反射がある場合とは「力の向きの速度成分が反転する軌道」と定義しよう。今の場合上昇して最上点に達し下降する軌道が反射のある場合と言える。力は\(y\)方向で、\(y\)方向の速度成分が\(-\to 0\to +\)と変化しているからである。
一様重力場の\(W\)は、上昇しているときは
\[
W_-=p_x x-\int^y\sqrt{2m\left(E-\frac{p_x^2}{2m}+mgy'\right)}dy'
\]
であり、下降しているときは
\[
W_+=p_x x+\int^y\sqrt{2m\left(E-\frac{p_x^2}{2m}+mgy'\right)}dy'
\]
である。
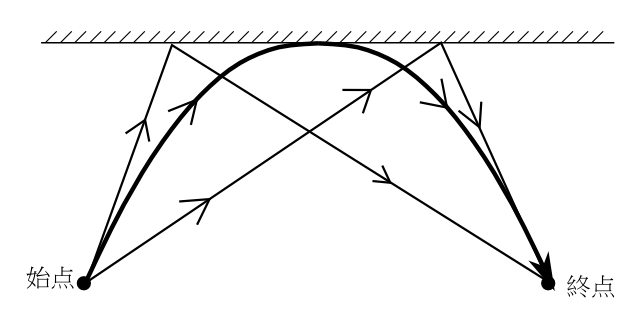
図8-9のように始点Aを出発して最上点Bに達し、始点と同じ高さの終点Cに戻ってくる軌道を考えよう。始点から最上点までは\(W_-\)を用い、最上点から終点までは\(W_+\)を用いなければならない。2つの\(W\)を用いなければならない。
積分定数を適当に決めればこの軌道の始点から終点まで\(W\)を連続にすることができる。そしてWの差が等しくなるように等高線を引く。直線ACを通る軌道を考えよう。
始点から最上点の等高線に対応するのは図8-9のように直線AEである。又、最上点から終点までの等高線に対応するのは図8-9のように直線DCである。直線DEの区間では等高線が重なってしまい、
ABCの軌道の作用積分の方が直線ACの作用積分より小さいとはいえないのである。
このようなことは力の向きの運動量が反転する場合は常に起こることなのではないかと思う。万有引力形のポテンシャルの場合も1つの連続な\(W\)では近日点から遠日点までしか表現できなかった。遠日点に達すれば\(\pm\)を反転した\(W\)を使わなければならなかった。
仮説
一般にはどの力学の法則を満たす軌道に対してもそれに対応するハミルトンヤコビの方程式の解が存在すると思う。だから一様重力場の考察から推察すると、一般に
仮説8-1
力学の法則を満たす反射のない軌道は最小軌道である。
ということが成り立つのではないかと思う。
図8-10 同じ高さまで到達する軌道同士での作用積分を比較すれば、力学の法則を満たす軌道が最も小さくなるのではないか。
また反射のある力学の法則を満たす軌道は最小軌道でないのだが、比較するのを反射のあるもの同士で比較したらどうだろうか。例えば一様重力場では図8-10のように最高点と同じ高さに到達する軌道同士で比べるわけである。そうすると力学の法則を満たす軌道の作用積分が一番小さくなるのではないかと思う。
仮説8-2
反射のある者同士で比べれば力学の法則を満たす軌道の作用積分が一番小さい。
ということが成り立つのではないかと思う。
8-6節 最小時間、フェルマの原理との類似
作用積分
\(\int_\alpha p ds\)というのは単なる運動量の線積分で、簡単な物理量に結びついたものではない。そこでこの量について、やや強引だが解釈を加えてみよう。ハミルトンヤコビの方程式の解\(S\)を使って波動関数を
\[
\psi\cong\exp\left(i\frac{S}{\hbar}\right)
\]
と近似した場合、位相の速さ\(v'\)は
\(
v'=E/p
\)
であると述べた(6章の式(24)参照)。だから
\[
v'=\frac{E}{\sqrt{2m[E-V(\mathbf{r})]}}
\]
である。
この\(v'\)を使うと作用積分は
\[
\int_\alpha\sqrt{2m[E-V(\mathbf{r})]}\;ds=E\int_\alpha\frac{ds}{v'(\mathbf{r})}
\]
と書ける。\(ds/v'(\mathbf{r})\)というのは速さ\(v'\)で動くものが距離\(ds\)進むのに必要な時間である。だから作用積分は位相速さで動く何者かが(そんなものはないのだが)、軌道の始点から終点に着くまでにかかる時間に系のエネルギー\(E\)を掛けたものである。系のエネルギーは同一のものを比較するので、作用積分が最小の経路は所要時間が最小の経路である。だから
定理8-3
仮説8-1、8-2が正しいなら、位相速さで動く何者かが
ある点からある点まで着くのにかかる時間は経路をいろいろ変えたとき、力学の法則を満たす軌道で最小になる
と言える。
これは光学のフェルマの原理に似ている。フェルマの原理は光の軌道は最も所要時間が短い経路を通る。というものである。
線積分
\(\int_\alpha \sqrt{2m(E-V)}\;ds\)
を作用積分という。始点と終点とエネルギーを固定して、経路を変えて作用積分の値を比較することがこの章の主題であった。作用積分は
\[
\int_\alpha p(\mathbf{r})ds
,\quad\int_\alpha |\nabla W|ds
,\quad\int_0^{t(\alpha)}2T[\mathbf{r^\alpha}(t)]dt
,\quad\int_0^{t(\alpha)}L\left[\mathbf{{r}^\alpha}(t),\mathbf{\dot{r}^\alpha}(t)\right]+E\;dt
\]
とも書ける。
力学の法則を満たす軌道は停留軌道になることを証明した。その逆は証明できなかった。
力学の法則を満たす軌道に対応する\(W\)が存在するときは、
その\(W\)の定義域内に入っている軌道の中では、力学の法則を満たす軌道が最小である。
だから\(W\)の定義域が作用積分の定義域を包み込んでいれば、力学の法則を満たす軌道は最小軌道になるといえる。しかし一様重力場の例で見たように包み込んでいない。だから最小軌道になると証明はできていない。そして証明の前提となるべき、
力学の法則を満たす軌道に対応する\(W\)が必ず存在するということを証明していない。ただこれは存在すると思う。
又、力学の法則を満たす軌道は最小軌道になると思っている。反射のある場合は2つの\(W\)が必要となる。だから最小軌道にならないのである。ただこれも想像だが、反射のある者同士で比べれば最小になるのではと思っている。
力学の法則を満たす軌道が作用積分の最小値をとるということは次のように言い換えられる。
シュレディンガーの波動方程式の解を
\[
\psi\cong\exp\left(i\frac{S}{\hbar}\right)
\]
と近似して、速度場としてこの波動関数
の位相速度を使うと、この位相速度で動く何者かは、力学の法則を満たす軌道を通ると所要時間が最も短くなる。これは光学のフェルマの原理と同じものである。しかしあくまでも
\(\psi\cong\exp\left(i\frac{S}{\hbar}\right)\)
という近似での位相速度である。これが何か深い意味があるのかは私には不明である。
多粒子系での最小作用の原理
このテキストでは、系を1粒子の場合に限定して話を進めてきたが、今まで述べてきた命題が多粒子系の場合どうなるかについて簡単に言及したい。
作用積分\(\int_\alpha \sqrt{2m(E-V)}\,ds\)での\(m\)というのは質量であり、多粒子系では各質量が等しいとは限らないので、この作用積分は意味をなさない。そこで
多粒子系の作用積分は
\[
\int_\alpha \sum_ip_i dx_i
\]
と定義される。
ここで\(dx_i\)は経路の微小変位ベクトルである。\(p_i\)は\(m_iv_i\)のことであり、\(v_i\)は
\[
\sum_i\frac{1}{2}m_iv_i^2+V=E
\]
を満たし、\(v_i\)は経路の向きと一致するとする。これで経路を決めれば各位置で\(v_i\)そして\(p_i\)が決まる。そして作用積分の値も決まる。1粒子の場合は\(p_i\)と\(dx_i\)の向きが一致するので
\[
\sum_i p_i dx_i=pds=\sqrt{2m(E-v)}\,ds
\]
となる。すなわち
この定義と\(\int_\alpha \sqrt{2m(E-v)}\,ds\)は一致する。多粒子の場合は各質量が同じとは限らないので
\[
p_idx_i\ne pds
\]
である。ここで\(p\)は\(p_i\)の大きさ。だから
\[
\int _\alpha \sum_ip_i dx_i\ne\int_\alpha pds
\]
である。例えば2粒子系である位置で、速度成分はすべて同じで、質量は一方の粒子が1,もう一方が2のとき、すなわち
\(v_i=(1,1,1,1,1,1),m_i=(1,1,1,2,2,2)\)のとき
\(p_i=(1,1,1,2,2,2)\)となり\(p_i\)の向きと\(v_i\)の向きは異なる。すなわち\(p_i\)の向きは経路の向きと異なるわけである。もちろん6次元では幾何学的な意味での経路の向きなどはないので、経路上の微小変位ベクトル\(dx_i\)と\(p_i\)が比例していないという意味である。
尚、\(\int_\alpha\sum_i p_i dx_i\)を一般座標\(q'\)と、それに対応する一般化運動量は\(p'\)で表すと
\[
p_i=\sum_\beta\frac{\partial\, q'_\beta}{\partial\, x_i}p'_\beta
\qquad\qquad
dx_i=\sum_\lambda\frac{\partial\, x_i}{\partial\, q'_\lambda}dq'_\lambda
\]
である(定理4-3)。
だから
\[
\int_\alpha\sum_i p_i dx_i=\int_\alpha
\sum_i\left(\sum_\beta\frac{\partial\, q'_\beta}{\partial\, x_i}p'_\beta\right)
\left(\sum_\lambda\frac{\partial\, x_i}{\partial\, q'_\lambda}dq'_\lambda\right)
=
\int_\alpha\sum_\beta p'_\beta dq'_\beta
\]
となる。だから直交座標を用いずに、一般化座標・運動量\(q,p\)を用いて作用積分を
\[
\int_\alpha \sum_\beta p_\beta dq_\beta
\]
と定義してもよい。
停留性
1粒子での「力学の法則を満たす軌道は作用積分の停留軌道である」という命題は多粒子系ではどうなるか見てみよう。
\[
\int_\alpha \sum_i p_i dx_i=\int_0^{t(\alpha)} \sum_i p_i \frac{dx_i}{dt}dt
=\int_0^{t(\alpha)}2T\; dt=\int_0^{t(\alpha)} L+E \;dt
\]
と変形でき、1粒子の場合と同様に作用積分は\(\int_0^{t(\alpha)} L+E \;dt\)と表せる。
そして1粒子の場合と同じように計算して、2つの軌道\(\alpha,\beta\)の作用積分の差は
\[
I[\beta]-I[\alpha]\cong
\int_0^{t(\beta)}\sum_{i=1}^3 \left[\frac{\partial\, L_\alpha(t)}{\partial\, x_i}-\frac{d}{dt}\left(\frac{\partial\, L_\alpha(t)}{\partial\, \dot{x}_i}\right) \right]\delta x_i\;dt+
\sum_ip_i(A)\Delta x_i -
\int_{\Delta\alpha}\sum_i p_i dx_i
\]
となる。ここで\(\Delta x_i\)は点Aから点Bへの変位である。これは式(\ref{tyokusen})に対応している。そして1粒子系のときと同じ理由でこの第2項と第3項はキャンセルする。だから力学の法則を満たす軌道では
\[
I[\beta]-I[\alpha]\cong 0
\]
となる。すなわち多粒子系でも力学の法則を満たす軌道は停留軌道となる。
最小性
1粒子での定理8-2
「力学の法則を満たす軌道に対応する\(W\)の定義域内に入っている軌道の中では、力学の法則を満たす軌道が最小である」という命題は多粒子系ではどうなるか見てみよう。
1粒子での証明では力学の法則を満たす軌道は\(\frac{\partial\, W}{\partial\, x_i}\)と
向きが等しいということを使った。
多粒子系では一般には
\(p_i\)と\(dx_i\)の向きが一致しない。そして力学の法則を満たす軌道では\(p_i=\frac{\partial\, W}{\partial\, x_i}\)である。だから
多粒子径では力学の法則を満たす軌道と\(\frac{\partial\, W}{\partial\, x_i}\)は向きが一致しない。
そういうわけで多粒子系での定理8-2の主張は、少なくとも1粒子の場合に示した論法では、証明できないのである。ただ培風館の物理学辞典によると力学の法則を満たす軌道は極小軌道になると書いてある。