第9章　ファインマンの経路積分

この章ではファインマンの経路積分について簡単に紹介する。私自身、ファインマンの経路積分について詳しくないので、簡単に紹介するだけである。 これは変分法の知識が物理の理解に役立つ数少ない例である。 この章での経路というのはただの空間の経路ではなく、第7章と同様の時間の関数としての空間経路である。第8章で扱ったような空間経路という意味ではない。この章は量子力学のブラケットの取扱の知識を前提とした。ここでの説明は、JJ桜井の現代の量子力学（吉岡書店）で得た知識を元に記述している。

9-1節　シュレディンガー方程式のプロパゲーター

シュレディンガー方程式に従う量子状態というものは、初期状態\(\big|\phi_0\big>\)が与えられれば、時間\(t\)経過後の状態は \[ \exp\left(\frac{\hat{H}}{i\hbar}t\right)\big|\phi_0\big> \] と決まる。そして\(\mathbf{r}'\)での時間\(t\)経過後の波動関数\(\phi(\mathbf{r}',t)\)は \[ \phi(\mathbf{r}',t)= \big<\mathbf{r}'|\exp\left(\frac{\hat{H}}{i\hbar}t\right) |\phi_0\big> \] である。右辺に\(\big|\mathbf{r}\big>\big<\mathbf{r}\big|d\mathbf{r}\)を挟んで積分すると \[ \phi(\mathbf{r}',t)= \int_\mathbf{r} \big<\mathbf{r}'|\exp\left(\frac{\hat{H}}{i\hbar}t\right) |\mathbf{r}\big> \big<\mathbf{r}|\phi_0\big>d\mathbf{r} \] となる。 \[ K(\mathbf{r}',\mathbf{r},t)\equiv \big<\mathbf{r}'|\exp\left(\frac{\hat{H}}{i\hbar}t\right)|\mathbf{r}\big> \] とおけば \[ \phi(\mathbf{r}',t)= \int_\mathbf{r} K(\mathbf{r}',\mathbf{r},t) \phi_0(\mathbf{r}) d\mathbf{r} \] と書ける。ここで\(\phi_0(\mathbf{r})\)は\(\big<\mathbf{r}|\phi_0\big>\)のことで初期状態の波動関数である。この\(K(\mathbf{r}',\mathbf{r},t)\)をプロパゲーターと呼ぶ。定義からわかるように、これは時間発展演算子の位置基底表現であり、最初\(\mathbf{r}\)に局在していた波動関数が時間\(t\)後に\(\mathbf{r}'\)へ移る遷移振幅である。

さてこの\(K(\mathbf{r}',\mathbf{r},t)\)を経路積分の形に書き換えよう。そのためにまず、簡単な例として時間を\(t=\frac{t}{2}+\frac{t}{2}\)と分割しよう。するとプロパゲーターは次のように変形できる。 \begin{eqnarray} K(\mathbf{r}',\mathbf{r},t)&=& \big<\mathbf{r}'|\exp\left(\frac{\hat{H}}{i\hbar}\left(\frac{t}{2}+\frac{t}{2}\right)\right)|\mathbf{r}\big>\notag\\ &=& \big<\mathbf{r}'|\exp\left(\frac{\hat{H}}{i\hbar}\frac{t}{2}\right)\cdot\exp\left(\frac{\hat{H}}{i\hbar}\frac{t}{2}\right)|\mathbf{r}\big>\notag\\ &=& \int_{\mathbf{r}''}\big<\mathbf{r}'|\exp\left(\frac{\hat{H}}{i\hbar}\frac{t}{2}\right)|\mathbf{r}''\big>\big<\mathbf{r}''|\exp\left(\frac{\hat{H}}{i\hbar}\frac{t}{2}\right)|\mathbf{r}\big>d\mathbf{r}''\notag\\ &=& \int_{\mathbf{r}''}K(\mathbf{r}',\mathbf{r}'',t/2)\cdot K(\mathbf{r}'',\mathbf{r},t/2)d\mathbf{r}'' \label{kei21} \end{eqnarray} 時間\(t\)での\(\mathbf{r}\)から\(\mathbf{r}'\)への遷移振幅というものは、時間\(t/2\)での\(\mathbf{r}\)から\(\mathbf{r}''\)への遷移振幅に、時間\(t/2\)での\(\mathbf{r}''\)から\(\mathbf{r}'\)への遷移振幅を掛けたものを、すべての\(\mathbf{r}''\)で足し合わせたものになっている(図9-1参)。

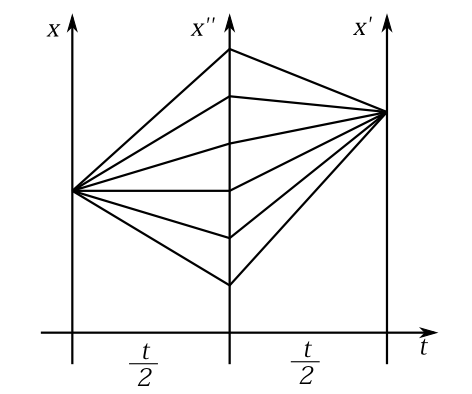
図9-1

式で書くと \(K(\mathbf{r}',\mathbf{r},t)\)は \[ K(\mathbf{r}',\mathbf{r}'',t/2)\cdot K(\mathbf{r}'',\mathbf{r},t/2)\Delta \mathbf{r}'' \] という数を、\(\mathbf{r}''\)を動かして、すべての経路について足し合わせたものになっている。今は時間を2等分したが、これは何等分でもいいわけで、一般に\(n\)等分としたら \(K(\mathbf{r}_n,\mathbf{r}_0,t)\)というのは

\begin{equation} K(\mathbf{r}_n,\mathbf{r}_0,t) =\int K(\mathbf{r}_n,\mathbf{r}_{n-1},t/n)\cdot K(\mathbf{r}_{n-1},\mathbf{r}_{n-2},t/n)\cdots K(\mathbf{r}_{1},\mathbf{r}_{0},t/n)\cdot d \mathbf{r}_{n-1} d\mathbf{r}_{n-2}\cdots d\mathbf{r}_{1} \label{kei1} \end{equation}

となる。これを経路積分と呼ぶ。位置基底でなく、運動量基底やエネルギー基底を使っても同様なことが言える。

9-2節　自由粒子のプロパゲーター

さて、次に自由粒子のプロパゲーターを具体的な形にしてみよう。要するに既知関数で表そうというわけである。 \(|\phi_i\big>\)を\(\hat{H}\)のエネルギー固有状態、\(E_i\)をそのエネルギー固有値とすると、\(K(\mathbf{r}',\mathbf{r},t)\)は \begin{eqnarray} K(\mathbf{r}',\mathbf{r},t)&=& \big<\mathbf{r}'|\exp\left(\frac{\hat{H}}{i\hbar}t\right)|\mathbf{r}\big>\notag\\ &=& \sum_{i,j} \big<\mathbf{r}'|\phi_i\big> \big<\phi_i| \exp\left(\frac{\hat{H}}{i\hbar}t\right)|\phi_j\big> \big<\phi_j|\mathbf{r}\big>\notag\\ &=& \sum_{i,j}\phi_i(\mathbf{r}')\big<\phi_i|\phi_j\big>\phi^*_j(\mathbf{r}) \exp\left(\frac{E_j}{i\hbar}t\right)\notag\\ &=& \sum_i \phi_i(\mathbf{r}')\phi^*_i(\mathbf{r})\exp\left(\frac{E_i}{i\hbar}t\right) \label{gut} \end{eqnarray} となる。自由粒子の場合、エネルギー固有値は \[ E_i=\frac{p_x^2+p_y^2+p_z^2}{2m} \] であり、固有関数は条件を使い周期を\(L\)として \[ \phi_i(\mathbf{r})=\frac{1}{\sqrt{L^3}}\exp\left[\frac{i}{\hbar}(p_x x+p_y y+p_z z)\right] \] である。\(p_x\)は周期境界条件のため、\(n\)を整数として \[ \frac{p_x}{\hbar}=\frac{2\pi}{L}n \] でなければならない。\(p_y,p_z\)も同様である (注　周期境界条件を使うというのは単に便宜上であって、要は\(\phi_i(\mathbf{r})\)が、その着目している空間を張ることができる基底になれればよいのである。それは\(L\to\infty\)すれば可能である。ここらへんは単に数学上の話なのであまり細かいことに拘らずに進んでもらいたい。)。 さて、これを式(\ref{gut})に入れてプロパゲーターを計算しよう。これからは退屈な作業なので、特に計算を追う必要はないであろう。結果だけみればいいと思う。

\begin{eqnarray} K(\mathbf{r}',\mathbf{r},t)&=& \sum_{\mathbf{p}} \exp\left[\frac{t}{i\hbar}\frac{p_x^2+p_y^2+p_z^2}{2m}\right]\frac{1}{\sqrt{L^3}}\exp\left[\frac{i}{\hbar}(p_x x'+p_y y'+p_z z')\right]\cdot \frac{1}{\sqrt{L^3}}\exp\left[\frac{i}{\hbar}(-p_x x-p_y y-p_z z)\right]\notag\\ &=& \sum_{p_x}\frac{1}{L}\exp\frac{i}{\hbar}\left(p_x(x'-x)-\frac{p_x^2}{2m}t\right)\cdot \sum_{p_y}\frac{1}{L}\exp\frac{i}{\hbar}\left(p_y(y'-y)-\frac{p_y^2}{2m}t\right)\cdot \sum_{p_z}\frac{1}{L}\exp\frac{i}{\hbar}\left(p_x(z'-z)-\frac{p_z^2}{2m}t\right) \notag \end{eqnarray}

となる。 \[ K_x\equiv \sum_{p_x}\frac{1}{L}\exp\frac{i}{\hbar}\left(p_x(x'-x)-\frac{p_x^2}{2m}t\right) \] と置こう。 \(K_y,K_z\)も同様に置く。すると \[ K(\mathbf{r}',\mathbf{r},t)=K_x\cdot K_y\cdot K_z \] となる。\(x,y,z\)成分とも同じなので、\(K_x\)だけ計算しよう。まず\(\exp\)の中を\(p_x\)の完全平方にする。すなわち \begin{equation} p_x(x'-x)-\frac{p_x^2}{2m}t=-\frac{t}{2m}\left(p_x-\frac{m(x'-x)}{t}\right)^2+\frac{m}{2}\frac{(x'-x)^2}{t} \label{kei41} \end{equation} とする。離散和\(\sum_{p_x}\)では計算できないので、\(L\to \infty\) として積分に置き換える。周期境界条件より \[ \frac{p_x}{\hbar}=\frac{2\pi}{L}n \quad \Longleftrightarrow \quad n=\frac{Lp_x}{2\pi \hbar} \] なので \begin{equation} \sum_{p_x}\quad\Longrightarrow\quad\frac{L}{2\pi \hbar}\int_\infty^\infty dp_x \label{kei42} \end{equation} と置き換えればよい。式(\ref{kei41})(\ref{kei42})から

\[ K_x=\frac{1}{2\pi\hbar}\exp\frac{i}{\hbar}\left[\frac{m}{2}\frac{(x'-x)^2}{t}\right] \int_\infty^\infty \exp \left[-\frac{it}{2m\hbar}\left(p_x-\frac{m(x'-x)}{t}\right)^2 \right] dp_x \]

となる。ここで積分変数を\(p_x\)から \[ \sqrt{\frac{t}{2m\hbar}} \left(p_x-\frac{m(x'-x)}{t}\right) =s \] と\(s\)に変換すると \[ K_x=\frac{1}{2\pi\hbar}\sqrt{\frac{2m\hbar}{t}}\exp\frac{i}{\hbar}\left[\frac{m}{2}\frac{(x'-x)^2}{t}\right] \int_\infty^\infty \exp (-is^2) ds \] となる。 \[ \int_\infty^\infty\exp (-is^2) ds=\sqrt{\frac{\pi}{i}} \] という公式を使うと \[ K_x=\sqrt{\frac{m}{2\pi i\hbar t}}\exp\frac{i}{\hbar}\left[\frac{m}{2}\frac{(x'-x)^2}{t}\right] \] となる。だから

3次元自由粒子のプロパゲーターは \[ K(\mathbf{r}',\mathbf{r},t)= \sqrt{\frac{m}{2\pi i\hbar t}}^{\;3}\exp\Bigg(\frac{i}{\hbar}\frac{m}{2}\left[\frac{(x'-x)^2}{t} +\frac{(y'-y)^2}{t} +\frac{(z'-z)^2}{t} \right]\Bigg) \] となる。

9-3節　ファインマンの経路積分の導出

\(\mathbf{r}\)から\(\mathbf{r}'\)へ時間\(t\)で動く力学の法則を満たす軌道のラグランジアンを時間\(t'\)の関数という意味で \[ L[\;\mathbf{r}',\mathbf{r},t\;](t'\,) \] と書こう。 \(\mathbf{r}=(x,y,z)\)から\(\mathbf{r}'=(x',y',z')\)へ時間\(t\)で動き、力学の法則を満たす軌道の、今の場合等速直線運動する軌道の、ラグランジアンの時間積分は \[ \int_0^t L[\;\mathbf{r}',\mathbf{r},t\;](t'\,)dt' = \frac{m}{2} \left[ \frac{(x'-x)^2}{t}+\frac{(y'-y)^2}{t}+\frac{(y'-y)^2}{t} \right] \] である。これを使うと

3次元自由粒子のプロパゲーターは \begin{equation} K(\mathbf{r}',\mathbf{r},t)= \sqrt{\frac{m}{2\pi i\hbar t}}^{\;3}\exp\left[\frac{i}{\hbar}\int_0^t L[\;\mathbf{r}',\mathbf{r},t\;](t'\,)dt' \right] \label{kei44} \end{equation} と書ける。

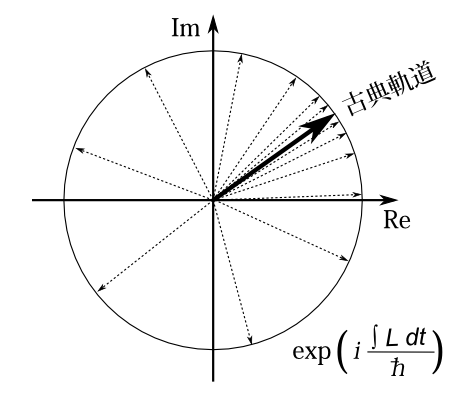
さて、プロパゲーターは時間を分割して経路の和で表すことが出来たのであった。例えば式(\ref{kei21})のように時間を2等分した場合、 \(K(\mathbf{r}',\mathbf{r},t)\)は \[ K(\mathbf{r}',\mathbf{r}'',t/2)\cdot K(\mathbf{r}'',\mathbf{r},t/2)\Delta \mathbf{r}'' \] という数を、\(\mathbf{r}''\)を動かして、すべての経路について足し合わせれば良いのであった。 式(\ref{kei44})を使うと、これは

\[ \sqrt{\frac{m}{2\pi i\hbar (t/2)}}^{\;3}\exp\left[\frac{i}{\hbar}\int_{t/2}^{t} L[\;\mathbf{r}',\mathbf{r''},t/2\;](t'\,)dt'\right] \cdot \sqrt{\frac{m}{2\pi i\hbar (t/2)}}^{\;3}\exp\left[\frac{i}{\hbar}\int_0^{t/2} L[\;\mathbf{r''},\mathbf{r},t/2\;](t'\,)dt' \right] \Delta \mathbf{r}'' \]

となり、これは

\[ \sqrt{\frac{m}{2\pi i\hbar (t/2)}}^{\;3\cdot 2}\exp\left[\frac{i}{\hbar} \left(\int_{t/2}^{t} L[\;\mathbf{r}',\mathbf{r''},t/2\;](t'\,)dt' + \int_0^{t/2} L[\;\mathbf{r}'',\mathbf{r},t/2\;](t'\,)dt'\right) \right] \Delta \mathbf{r}'' \]

と変形できる。 \[ \int_{t/2}^{t} L[\;\mathbf{r}',\mathbf{r}'',t/2\;](t'\,)dt' + \int_0^{t/2} L[\;\mathbf{r}'',\mathbf{r},t/2\;](t'\,)dt' \] は\(\mathbf{r}(0)\to \mathbf{r}''(t/2)\to \mathbf{r}'(t)\)を通る軌道のラグランジアンの時間積分であり、基本的には力学の法則を満たさない軌道である。\(\mathbf{r}''\)が変われば軌道も変わるので、 それぞれの軌道のラグランジアンを指標\(\lambda\)で区別して、時間\(t\)の関数としての\(L_\lambda(t)\)と書こう。 すると\(K(\mathbf{r}',\mathbf{r},t)\)は \[ K(\mathbf{r}',\mathbf{r},t) = \sqrt{\frac{m}{2\pi i\hbar (t/2)}}^{\;3\cdot 2}\int\exp\left[\frac{i}{\hbar} \left(\int_0^t L_\lambda(t')dt'\right)\right] d \mathbf{r}'' \] となる。 式(\ref{kei1})のように時間を\(n\)等分して、今と同様に考えれば

PDFファイルA4、158ページ、1.8MB

目次

序文

記号・用語

第1章

第2章

第3章

第4章

第5章

第6章

第7章

第8章

第9章

第10章

付録A

付録B

付録C

付録D

おわりに

積分の部分は \[ (d\mathbf{r})^{n-1}\sum_\lambda \exp\left[\frac{i}{\hbar}\int_0^tL_\lambda(t')dt'\right] \] と書いたほうがいろんな経路の和というて意味がよくわかるかもしれない。

さて、今はポテンシャルのない場合に式(\ref{kei46})の形の和でプロパゲーターを表せるということを示したのだが、ポテンシャルが存在するときは式(\ref{kei46})の形に表せるのだろうか。実は私はここらへんについては詳しくないのだが、時間の分割数\(n\to\infty\)とすれば、表せるようである。すなわち、ポテンシャルのある系でもプロパゲーターは指数にラグランジアンの時間積分をのせた、すべての経路の和で表せるというわけである。

このことをファインマンの経路積分という。

9-4節　変分法の停留との関係

プロパゲーターは \[ A\exp\left[\frac{i}{\hbar}\int_0^t L_1 dt'\right]+ A\exp\left[\frac{i}{\hbar}\int_0^t L_2 dt'\right]+ A\exp\left[\frac{i}{\hbar}\int_0^t L_3 dt'\right]+ \cdots\cdots \] の といろんな経路での\(A\exp\left[\frac{i}{\hbar}\int_0^t L_\lambda dt\right]\)を足すのであった。 ここで\(A\)は軌道と無関係な数であり \[ A= \sqrt{\frac{m}{2\pi i\hbar t/n}}^{\;3n} \cdot\Delta \mathbf{r}_{n-1}\Delta \mathbf{r}_{n-2}\cdots\Delta \mathbf{r}_{1} \] である。さてこの中で 一体どういう経路がその和に寄与するのだろうか。力学の法則を満たす軌道というのは汎関数 \[ I[x]=\int_0^tL(x,\dot{x},t')dt' \] の停留関数であった(定理7-4)。 ということは、その軌道をわずかにずらしても、この積分の値はほとんど変わらないということである。ということは \[ A\exp\left[\frac{i}{\hbar}\int_0^t L_{cl} dt'\right] \] に近い値を多く足すということである。\(L_{cl}\)は力学の法則を満たす軌道のラグランジアンである。

図9-2　\(\exp\left[\frac{i}{\hbar}\int _0^t Ldt'\right]\)を複素平面で表した図。

だから図9-2にあるように、位相の近いものの和は、プロパゲーターへの寄与が大きい。一方古典軌道からはずれると、\(\int_0^tLdt'\)は軌道をわずかにずらしても大きく変化する。ということは位相が大きく変化するのでプロパゲーターへの寄与は小さい。すなわち、力学の法則を満たす軌道とその周辺のみの軌道だけが寄与するということである。古典軌道から少しでもずれると\(\int_0^tLdt'\)が大きく変化するような系では古典軌道からの寄与が大きい。古典軌道から大きくずれても\(\int_0^tLdt'\)があまり変化しない系なら、そういう軌道もプロパゲーターに寄与するので、古典軌道からの寄与は小さくなる。同じポテンシャルで同じ軌道では、質量がより大きい粒子の方が古典軌道からの寄与が大きくなる。 これが変分法とファインマンの経路積分との関係である。思わぬところで古典力学と量子力学の関係があるものであり、おもしろいと思う次第である。しかしながら、このことが古典力学と量子力学の橋渡しになっているのかというと、少なくとも私には明瞭ではない。

9-5節　まとめ

シュレディンガー方程式の時間発展は初期状態\(|\phi_0\big>\)が決まれば一意的である。時間\(t\)経過後の状態は \[ \exp\left(\frac{\hat{H}}{i\hbar}t\right)|\phi_0\big> \] である。 これを位置表示したものが \[ \int K(\mathbf{r}',\mathbf{r},t) \phi_0(\mathbf{r}) d\mathbf{r} \] である。 \(K(\mathbf{r}',\mathbf{r},t)\)は演算子\(\exp\left(\frac{\hat{H}}{i\hbar}t\right)\)の位置基底表現による行列である。 この\(K\)は時間の関数としての経路の和で表せる。経路の和で表せるので経路積分と言おう。

ここまではどうってことない話である。ところがこの経路和というのが \[ A\exp\left[\frac{i}{\hbar}\int_0^t L_1 dt'\right]+ A\exp\left[\frac{i}{\hbar}\int_0^t L_2 dt'\right]+ A\exp\left[\frac{i}{\hbar}\int_0^t L_3 dt'\right]+ \cdots\cdots \] と表せるのである。このことはこのテキストでは自由粒子で証明しただけであるが、一般のポテンシャルでも成り立つようである。古典軌道は\(\int_0^t L dt'\)の停留関数である。すなわち多少軌道が変化しても\(\int_0^t L dt'\)の値はあまり変化しない。ということは経路和で効くのは古典軌道の近辺である。他の軌道は打ち消し合って和に寄与しない。だからある点からある点へある時間で移る遷移成分を計算するのに古典軌道のみを考慮すればいい近似になるということである。非常に面白い話なのだが、このことが量子力学のある極限が古典力学になるということを示しているわけでは全くない。