第2章 ラグランジュ方程式
最初に直交座標でのラグランジュ方程式というものを紹介する。ラグランジュ方程式とは何かというものを知りたければそこだけ読めばよい。その後、一般の座標でのラグランジュ方程式を紹介する。例を多く入れたが、それは抽象的な式変形だけでは意味がどこまで伝わるか不安であるし、言葉だけで概念は説明できないという考えからである。例から概念をくみ取ってもらいたい。本文の説明だけで意味がよく分かるなら、例はどんどん飛ばせば良いと思う。
2-1節 ラグランジュ方程式の紹介
まず簡単な例でラグランジュ方程式というものを紹介しよう。直線上を運動する質点の場合の運動方程式は \begin{equation} m\ddot{x}=F \label{nyuton} \end{equation} である。\(\ddot{x}\)は解析力学独特の記号で \[ \dot{x}\equiv\frac{dx}{dt},\qquad \ddot{x}\equiv\frac{d^2x}{dt^2} \] のことである。運動エネルギー \[T=\frac{1}{2}m\dot{x}^2\] を使うと、\(m\ddot{x}\)は \begin{equation} m\ddot{x} =\frac{d}{dt}\left(\frac{\partial\, T}{\partial\, \dot{x}}\right)-\frac{\partial\, T}{\partial\, x} \label{ww1} \end{equation} と書き換えられることは容易にわかろう(注 \(\frac{\partial\, T}{\partial\, x}\)は今の場合必要ないが今後必要なので入れた)。 だから式(\ref{nyuton})は \[ \frac{d}{dt}\left(\frac{\partial\, T}{\partial\, \dot{x}}\right)-\frac{\partial\, T}{\partial\, x}=F \] と同じことである。これをラグランジュ方程式という。これは単に運動方程式を書き換えただけである。力が \(F=-\frac{\partial\, V}{\partial\, x}\)とポテンシャル\(V\)から導かれるときは \[ \frac{d}{dt}\left(\frac{\partial\, T}{\partial\, \dot{x}}\right)-\frac{\partial\, T}{\partial\, x}=-\frac{\partial\, V}{\partial\, x} \] となる。\(V\)は\(\dot{x}\)を含んでなく、\(T\)は\(x\)を含んでいないので、さらに \[ \frac{d}{dt}\left(\frac{\partial\, (T-V)}{\partial\, \dot{x}}\right)=\frac{\partial\, (T-V)}{\partial\, x} \] と書き換えられる。 ラグランジアン \[ L\equiv T-V \] というものを定義し、これを使うと \[ \frac{d}{dt}\left(\frac{\partial\, L}{\partial\, \dot{x}}\right)=\frac{\partial\, L}{\partial\, x} \] と書き換えられる。 これもラグランジュ方程式という。
今の話は1次元でなくとも、又、粒子が何個あっても同様で、今と全く同じように以下のことが言える。
定理2-1(直交座標でのラグランジュ方程式)
質点が\(n\)個のときの\(3n\)個の直交座標の運動方程式
\begin{equation}
m_i\ddot{x}_i=F_i\qquad \qquad(i=1,2,3\cdots 3n)
\label{l61}
\end{equation}
は運動エネルギー
\[
T=\sum_{i=1}^{3n}\frac{1}{2}m_i\dot{x}_i^2
\]
を使うと、
\begin{equation}
\frac{d}{dt}\left(\frac{\partial\, T}{\partial\, \dot{x}_i}\right)-\frac{\partial\, T}{\partial\, x_i}=F_i
\label{lat}
\end{equation}
と書き換えられる。そして力が\(F_i=-\frac{\partial\, V}{\partial\, x_i}\)とポテンシャル\(V\)から導かれるときはラグランジアン
\[
L\equiv T-V
\]
というものを定義し、それを使うと
\begin{equation}
\frac{d}{dt}\left(\frac{\partial\, L}{\partial\, \dot{x}_i}\right)=\frac{\partial\, L}{\partial\, x_i}
\label{lat2}
\end{equation}
と書ける。式(\ref{lat})(\ref{lat2})もラグランジュ方程式という。式(\ref{lat2})は式(\ref{lat})の特別な場合である。
今は直交座標でこのラグランジュ方程式が成り立つことを示したのだが、実はどんな座標でも成り立つ(注 細かいことを言えば式(\ref{lat})の右辺は少し異なる)。それを今から述べていく。
2-2節 一般座標でのラグランジュ方程式
さて準備ができたので一般座標でのラグランジュ方程式というものを説明しよう。一般座標というのは、直交座標を含めた任意の座標という意味である。ニュートンの運動法則を直交座標で書くと \[ m\ddot{x}=F \] である。今、質点が\(n\)個あるとすると、この式は\(3n\)個あることになる。各式に番号をふると \begin{equation} m_i\ddot{x}_i=F_i\qquad i=1,2\cdots 3n \label{tyo} \end{equation} と書ける。さて、この\(x_i\)の可能な運動を\(3n\)個又はそれより少ない変数\(q_\alpha\)と\(t\)の関数で表せたとしよう。すなわち \begin{eqnarray} &&x_1=x_1(q_1,q_2,\cdots q_k, t)\notag\\ &&x_2=x_2(q_1,q_2,\cdots q_k, t)\notag\\ &&\cdots\cdots\cdots\cdots\cdots\cdots\cdots\notag\\ &&x_{3n}=x_{3n}(q_1,q_2,\cdots q_k, t)\notag \end{eqnarray} ということである。 \(q_\alpha\)が\(3n\)個あるときとは、拘束条件がないときである。拘束条件が1つあれば\(q_\alpha\)は\(3n-1\)個、2個なら\(q_\alpha\)は\(3n-2\)個、拘束条件が1つ増えるごとに\(q_\alpha\)の自由度が1つ減るわけである。拘束条件とは、例えば粒子が球面上しか動けないとか、2つの粒子の距離が不変に保たれているなどのように運動を制限するものである。さて式(\ref{tyo})に\(\frac{\partial\, x_i}{\partial\, q_\alpha}\)を掛けて、\(i\)で和をとった \begin{equation} \sum_i\frac{\partial\, x_i}{\partial\, q_\alpha}m_i\ddot{x}_i=\sum_i\frac{\partial\, x_i}{\partial\, q_\alpha}F_i \label{lah} \end{equation} が実質的なラグランジュ方程式の内容を表す式である。というのは、この左辺を、恒等式に置き換えたものがラグランジュ方程式だからである。もちろん、世間一般ではラグランジュ方程式とは呼ばれてはいない。 これは行列で書くと \[ \left( \begin{array}{ccc} \frac{\partial\, x_1}{\partial\, q_1}&\frac{\partial\, x_2}{\partial\, q_1}&\cdots\\ \frac{\partial\, x_1}{\partial\, q_2}&\frac{\partial\, x_2}{\partial\, q_2}&\cdots\\ \cdots&\cdots&\cdots\\ \end{array} \right) \left( \begin{array}{c} m_1 \ddot{x}_1\\ m_2 \ddot{x}_2\\ \cdots\\ \end{array} \right) = \left( \begin{array}{ccc} \frac{\partial\, x_1}{\partial\, q_1}&\frac{\partial\, x_2}{\partial\, q_1}&\cdots\\ \frac{\partial\, x_1}{\partial\, q_2}&\frac{\partial\, x_2}{\partial\, q_2}&\cdots\\ \cdots&\cdots&\cdots\\ \end{array} \right) \left( \begin{array}{c} F_1\\ F_2\\ \cdots\\ \end{array} \right) \] となる。 この左辺を変形しよう。式(\ref{ww1})で見たように \[ m_i\ddot{x}_i=\frac{d}{dt}\left(\frac{\partial\, T}{\partial\, \dot{x}_i}\right)-\frac{\partial\, T}{\partial\, x_i} \] と変形できた。だがら \[ \sum_i\frac{\partial\, x_i}{\partial\, q_\alpha}m_i\ddot{x}_i= \sum_i\frac{\partial\, x_i}{\partial\, q_\alpha} \left[\frac{d}{dt}\left(\frac{\partial\, T}{\partial\, \dot{x}_i}\right)-\frac{\partial\, T}{\partial\, x_i}\right] \] と書き換えられる。 \(T\)は\(\dot{x}_i\)の関数であり、\(\ddot{x}_i\)以上を含んでいないので定理1-2が使える。これを使うと \[ \frac{d}{dt}\left(\frac{\partial\, T}{\partial\, \dot{q}_\alpha}\right)-\frac{\partial\, T}{\partial\, {q}_\alpha} =\sum_i\frac{\partial\, x_i}{\partial\, q_\alpha} \left[\frac{d}{dt}\left(\frac{\partial\, T}{\partial\, \dot{x}_i}\right)-\frac{\partial\, T}{\partial\, x_i}\right] \] である。だから式(\ref{lah})の左辺は
(恒等式) \begin{equation} \sum_i\frac{\partial\, x_i}{\partial\, q_\alpha}m_i\ddot{x}_i = \frac{d}{dt}\left(\frac{\partial\, T}{\partial\, \dot{q}_\alpha}\right)-\frac{\partial\, T}{\partial\, {q}_\alpha} \label{l615} \end{equation}
と書き換えられる。これは最も重要な恒等式である。一方式(\ref{lah})の右辺は 一般化力というもので \begin{equation} f_\alpha\equiv \sum_i\frac{\partial\, x_i}{\partial\, q_\alpha}F_i \label{l152} \end{equation} と定義される。恒等式(\ref{l615})と定義式(\ref{l152})を使うと式(\ref{lah})は
(ラグランジュ方程式) \begin{equation} \frac{d}{dt}\left(\frac{\partial\, T}{\partial\, \dot{q}_\alpha}\right)-\frac{\partial\, T}{\partial\, {q}_\alpha}=f_\alpha \label{lah2} \end{equation}
と書き換えられる。この方程式をラグランジュ方程式という。
ところで \[ \sum_i F_i \Delta x_i \] は変位が\(\Delta x_i\)のときの力\(F_i\)がする仕事量である。\(\Delta x_i\)を\(\Delta q_\alpha\)の変位に対応する変位とし、この式を\(\Delta q_\alpha\)で割ると \[ \sum_i F_i \frac{\Delta x_i}{\Delta q_\alpha}\qquad\Longrightarrow\qquad \sum_i F_i \frac{\partial\, x_i}{\partial\, q_\alpha} \] である。よって
定理2-2 一般化力\(f_\alpha\)とは座標\(q_\alpha\)の単位変位あたりの仕事量である。
と言える。だから\(q_\alpha\)の変位に対して仕事をしないような力は一般化力から削除してよい。
2-3節 例
例2-1 平面極座標でのラグランジュ方程式
平面極座標でのラグランジュ方程式(\ref{lah2})を作ってみよう。 \[ x=r\cos\theta\qquad y=r\sin\theta \] とすると、 \[ \dot{x}=\dot{r}\cos\theta-r\sin\theta\cdot\dot{\theta} \qquad \dot{y}=\dot{r}\sin\theta+r\cos\theta\cdot\dot{\theta} \] となる。だから運動エネルギー\(T\)は \begin{eqnarray} T&=&\frac{1}{2}m(\dot{x}^2+\dot{y}^2)\notag\\ &=&\frac{1}{2}m(\dot{r}^2+r^2\dot{\theta}^2) \label{tu1} \end{eqnarray} となる。だからラグランジュ方程式(\ref{lah2})は\(r\)成分に関しては \begin{equation} m\ddot{r}-mr\dot{\theta}^2=f_r \label{rsei} \end{equation} となる。ここで\(f_r\)は\(r\)成分に関する一般化力。\(\theta\)成分に関しては \begin{equation} \frac{d}{dt}(mr^2\dot{\theta})=f_\theta \label{thea} \end{equation} となる。ここで\(f_\theta\)は\(\theta\)成分に関する一般化力。【例終】
例2-2 平面極座標での恒等式(\ref{l615})の確認
ラグランジュ方程式(\ref{lah2})を導くにあたって \begin{equation} \sum_i\frac{\partial\, x_i}{\partial\, q_\alpha}m_i\ddot{x}_i = \frac{d}{dt}\left(\frac{\partial\, T}{\partial\, \dot{q}_\alpha}\right)-\frac{\partial\, T}{\partial\, {q}_\alpha} \label{lb10} \end{equation} という恒等式を使った。これが極座標で成り立っていることを確認してみよう。 左辺は今の場合、行列で表せば \begin{equation} m \left( \begin{array}{cc} \frac{\partial\, x}{\partial\, r}&\frac{\partial\, y}{\partial\, r}\\ \frac{\partial\, x}{\partial\, \theta}&\frac{\partial\, y}{\partial\, \theta} \end{array} \right) \left( \begin{array}{c} \ddot{x}\\ \ddot{y} \end{array} \right) \label{gyou} \end{equation} である。 \[ x=r\cos\theta\qquad y=r\sin\theta \] を時間で2階微分すると \begin{eqnarray} \ddot{x}&=&\ddot{r}\cos\theta-2\,\dot{r}\,\dot{\theta}\sin\theta-r\,\ddot{\theta}\sin\theta-r\,\dot{\theta}^2\cos\theta\notag\\ \ddot{y}&=&\ddot{r}\sin\theta+2\,\dot{r}\,\dot{\theta}\cos\theta+r\,\ddot{\theta}\cos\theta-r\,\dot{\theta}^2\sin\theta \label{lb8} \end{eqnarray} となる。又 \begin{equation} \left( \begin{array}{cc} \frac{\partial\, x}{\partial\, r}&\frac{\partial\, y}{\partial\, r}\\ \frac{\partial\, x}{\partial\, \theta}&\frac{\partial\, y}{\partial\, \theta} \end{array} \right) = \left( \begin{array}{cc} \cos\theta&\sin\theta\\ -r\sin\theta&r\cos\theta \end{array} \right) \label{lb9} \end{equation} である。式(\ref{lb8})(\ref{lb9})を式(\ref{gyou})に代入すると \[ m \left( \begin{array}{c} \ddot{r}-r\dot{\theta}^2\\ r^2\ddot{\theta}+2r\dot{r}\dot{\theta} \end{array} \right) \] となる。これはそれぞれ、式(\ref{rsei})と(\ref{thea})の左辺に一致している。恒等式(\ref{lb10})が平面極座標で成り立っていることが確認できた。【例終】
例2-3 重心・相対座標のラグランジュ方程式
粒子が2つの場合の、いわゆる重心・相対座標のラグランジュ方程式(\ref{lah2}) を作ろう。簡単のため1次元とする。重心座標\(x_g\)、相対座標\(x_s\)は \[ \text{(重心座標)}\quad x_g=\frac{m_1x_1+m_2x_2}{m_1+m_2}\qquad\qquad \text{(相対座標)}\quad x_s=x_2-x_1 \] である。添字の\(1,2\)は粒子を区別する指標。これを逆に解くと \begin{equation} x_1=x_g-\frac{m_2}{m_1+m_2}x_s\qquad x_2=x_g+\frac{m_1}{m_1+m_2}x_s \label{jcd} \end{equation} である。だから運動エネルギー\(T\)は \begin{eqnarray} T&=&\frac{1}{2}m_1\left(\dot{x}_g-\frac{m_2}{m_1+m_2}\dot{x}_s\right)^2+ \frac{1}{2}m_2\left(\dot{x}_g+\frac{m_1}{m_1+m_2}\dot{x}_s\right)^2\notag\\[3mm] &=& \frac{1}{2}(m_1+m_2){\dot{x}_g}^{\;2}+\frac{1}{2}\frac{m_1m_2}{m_1+m_2}{\dot{x}_s}^{\;2} \label{lb5} \end{eqnarray} となる。だからラグランジュ方程式(\ref{lah2})の左辺はそれぞれ \begin{equation} \frac{d}{dt}\left(\frac{\partial\, T}{\partial\, \dot{x}_g}\right)-\frac{\partial\, T}{\partial\, x_g}=(m_1+m_2)\ddot{x}_g \qquad \frac{d}{dt}\left(\frac{\partial\, T}{\partial\, \dot{x}_s}\right)-\frac{\partial\, T}{\partial\, x_s}=\frac{m_1m_2}{m_1+m_2}\ddot{x}_s \label{j78} \end{equation} となる。重心座標と相対座標の一般化力\(f_{g},f_{s}\)は、粒子1,2にかかる力をそれぞれ\(F_1,F_2\)とすると \[ \left( \begin{array}{c} f_{g}\\ f_{s} \end{array} \right) = \left( \begin{array}{cc} \frac{\partial\, x_1}{\partial\, x_g}&\frac{\partial\, x_2}{\partial\, x_g}\\ \frac{\partial\, x_1}{\partial\, x_s}&\frac{\partial\, x_2}{\partial\, x_s} \end{array} \right) \left( \begin{array}{c} F_{1}\\ F_{2} \end{array} \right) \] であり、 式(\ref{jcd})より \begin{eqnarray} \left( \begin{array}{c} f_{g}\\ f_{s} \end{array} \right) &=& \left( \begin{array}{cc} 1&1\\[2mm] \displaystyle-\frac{m_2}{m_1+m_2}&\displaystyle\frac{m_1}{m_1+m_2}\\ \end{array} \right) \left( \begin{array}{c} F_{1}\\ F_{2} \end{array} \right)\notag\\[3mm] &=& \left( \begin{array}{c} F_{1}+F_2\\[2mm] \displaystyle-\frac{m_2}{m_1+m_2}F_1+\frac{m_1}{m_1+m_2}F_{2} \end{array} \right)\notag \end{eqnarray} となる。だからラグランジュ方程式(\ref{lah2})は \[ (m_1+m_2)\ddot{x}_g=F_{1}+F_{2}\qquad \frac{m_1m_2}{m_1+m_2}\ddot{x}_s=-\frac{m_2}{m_1+m_2}F_{1}+\frac{m_1}{m_1+m_2}F_{2} \] となる。【例終】
例2-4 重心相対座標での恒等式(\ref{l615})の確認
再び恒等式 \[ \sum_i\frac{\partial\, x_i}{\partial\, q_\alpha}m_i\ddot{x}_i = \frac{d}{dt}\left(\frac{\partial\, T}{\partial\, \dot{q}_\alpha}\right)-\frac{\partial\, T}{\partial\, {q}_\alpha} \] が重心相対座標で成り立っていることを確認してみよう。 左辺は \begin{eqnarray} \left( \begin{array}{cc} \frac{\partial\, x_1}{\partial\, x_g}&\frac{\partial\, x_2}{\partial\, x_g}\\ \frac{\partial\, x_1}{\partial\, x_s}&\frac{\partial\, x_2}{\partial\, x_s} \end{array} \right) \left( \begin{array}{c} m_1\ddot{x}_1\\ m_2\ddot{x}_2 \end{array} \right) &=& \left( \begin{array}{cc} 1&1\\[2mm] \displaystyle-\frac{m_2}{m_1+m_2}&\displaystyle\frac{m_1}{m_1+m_2}\\ \end{array} \right) \left( \begin{array}{c} m_1\ddot{x}_1\\ m_2\ddot{x}_2 \end{array} \right)\notag\\[3mm] &=& \left( \begin{array}{c} m_1\ddot{x}_1+m_2\ddot{x}_2\\[2mm] \displaystyle-\frac{m_2m_1\ddot{x}_1}{m_1+m_2}+\frac{m_1m_2\ddot{x}_2}{m_1+m_2}\\ \end{array} \right)\notag\\[3mm] &=& \left( \begin{array}{c} (m_1+m_2)\ddot{x}_g\\[2mm] \displaystyle\frac{m_1m_2}{m_1+m_2}\ddot{x}_s\\ \end{array} \right)\notag \end{eqnarray} となり、式(\ref{j78})で計算したものと一致していることがわかる。【例終】
2-4節 力が、ポテンシャルからの力と仕事をしない力から構成されている場合
今、力が、ポテンシャルからの力と可能な変位に対して仕事をしない力の和で構成されている場合を考えよう。すなわち
条件1 力の直交座標成分\(F_i\)が \[ F_i=-\frac{\partial\, V}{\partial\, x_i}+\mathcal{K}_i \] と書けて、\(K_i\)は、\(q_\alpha\)の変位に対して仕事をしない、すなわち \begin{equation} \sum_i\frac{\partial\, x_i}{\partial\, q_\alpha}\mathcal{K}_i=0 \label{lb1} \end{equation} を満たす
としよう。このとき一般化力\(f_\alpha\)は \[ f_\alpha=\sum_i\frac{\partial\, x_i}{\partial\, q_\alpha}\left(-\frac{\partial\, V}{\partial\, x_i}+\mathcal{K}_i\right)=-\frac{\partial\, V}{\partial\, q_\alpha} \] となってくれる。だからラグランジュ方程式(\ref{lah2})は \begin{equation} \frac{d}{dt}\left(\frac{\partial\, T}{\partial\, \dot{q}_\alpha}\right)-\frac{\partial\, T}{\partial\, {q}_\alpha} =-\frac{\partial\, V}{\partial\, q_\alpha} \label{lav} \end{equation} となる。この条件1を満たす場合は非常に多い(注 拘束力は私の知る限り必ず式(\ref{lb1})を満たす)。その結果ラグランジュ方程式の一般化力が\(-\frac{\partial\, V}{\partial\, q_\alpha}\)と単純なものになる。これこそが\(m_i\ddot{x}_i=F_i\)に\(\frac{\partial\, x_i}{\partial\, q_\alpha}\)を掛けて、\(i\)で和をとった理由である。もしこのようにラグランジュ方程式の一般化力が簡単にならないなら、\(\frac{\partial\, x_i}{\partial\, q_\alpha}\)を掛ける必要など全くなく、\(\frac{\partial\, q_\alpha}{\partial\, x_i}\)でもいいし、又は他の数でもよいのである。さてラグランジアン\(L\)を \[ L\equiv T-V \] と定義すると式(\ref{lav})は \[ \frac{d}{dt}\left(\frac{\partial\, L}{\partial\, \dot{q}_\alpha}\right)=\frac{\partial\, L}{\partial\, {q}_\alpha} \] と書ける。この式はラグランジュ方程式として最もポピュラーな形である。これは式(\ref{lah2})の特別な場合なのだが、普通、ラグランジュ方程式といえばこの式のことである。まとめると
定理2-3 (ラグランジュ方程式)
系が条件1を満たすときはラグランジュ方程式(\ref{lah2})は
\begin{equation}
\frac{d}{dt}\left(\frac{\partial\, L}{\partial\, \dot{q}_\alpha}\right)\equiv\frac{\partial\, L}{\partial\, {q}_\alpha}
\label{lah4}
\end{equation}
と書ける。ここで\(L\)はラグランジアンといい
\[
L=T-V
\]
で定義される。
2-5節 ラグランジュ方程式の例
例2-5 中心力ポテンシャル
例えば力が万有引力のように\(r\)のみの関数のポテンシャル\(V\)から導かれるときは ラグランジュ方程式として式(\ref{lah4})が使える。運動エネルギーとして式(\ref{tu1})の結果を使うと、ラグランジアンは、 \begin{equation} L=\frac{1}{2}m(\dot{r}^2+r^2\dot{\theta}^2)-V(r) \label{lb2} \end{equation} となる。 \(r\)成分のラグランジュ方程式は \begin{equation} m\ddot{r}=mr\dot{\theta}^2-\frac{\partial\, V}{\partial\, r} \label{tuika13} \end{equation} \(\theta\)成分に関しては \[ \frac{d}{dt}(mr^2\dot{\theta})=0 \] となる。尚、\(\theta\)成分のラグランジュ方程式は角運動量が一定であることを述べている。【例終】
例2-6 2点間の距離に依存するポテンシャル
2点間の距離のみに依存するポテンシャルからの力でそれ以外はないとき。例えば2つの粒子がバネでつながれているときなどである。このときもラグランジュ方程式として式(\ref{lah4})が使える。1次元とすると重心・相対座標のラグランジアンは式(\ref{lb5})を使って \[ L=\frac{1}{2}(m_1+m_2){\dot{x}_g}^2+\frac{1}{2}\frac{m_1m_2}{m_1+m_2}{\dot{x}_s}^2-V(x_s) \] となる。だからラグランジュ方程式は \[ (m_1+m_2)\ddot{x}_g=0\qquad \frac{m_1m_2}{m_1+m_2}\ddot{x}_s=-\frac{\partial\, V}{\partial\, x_s} \] となる。【例終】
例2-7 拘束力のある運動、半径一定
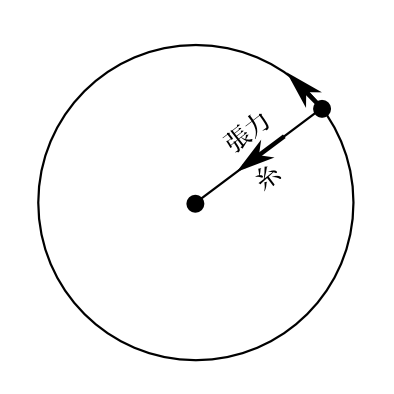
図2-1 糸の張力によって円上を運動する粒子。拘束力である糸の張力は仕事をしない。
図2-1のように一端が固定されたひもに結び付けられた質点があるとしよう。この場合運動は\(\theta\)のみによって表される。力は糸の張力なので運動方向に直角で 仕事をしない。だからラグランジュ方程式として式(\ref{lah4})が使える。平面極座標でのラグランジアンは式(\ref{lb2})で\(\dot{r}=0,V=0\) とした \[ L=\frac{1}{2}m(r^2\dot{\theta}^2) \] である。だからラグランジュ方程式は \begin{equation} mr^2\ddot{\theta}=0 \label{la91} \end{equation} となる。
拘束力を求めてみよう。 \[ m\ddot{x}=F_x\qquad m\ddot{y}=F_y \] に式(\ref{la91})の方程式の解を入れて\(F_x,F_y\)を求めれば良い。今の場合 \[ x=r\cos\theta\qquad y=r\sin\theta \] を\(\dot{r}=\ddot{\theta}=0\)に注意して微分すると \[ F_x=m\ddot{x}=-mr\dot{\theta}^2\cos\theta \qquad F_y=m\ddot{x}=-mr\dot{\theta}^2\sin\theta \] となり、張力である\(F\)の大きさは\(mr\dot{\theta}^2\)で向きは回転の中心方向だとわかる (注 しかし今の場合別の方法でも拘束力を求めることができる。 3-2節の例3-1で述べるが、 \(r\)成分の一般化力\(f_r\)というのは、 力の半径方向の成分(正射影)となっている。 だから\(f_r\)は糸の張力になっているのである。そして式(\ref{rsei})から \[ f_r=-mr\dot{\theta}^2 \] と求まる。)。【例終】
例2-8 拘束力のある運動、2点間の距離一定
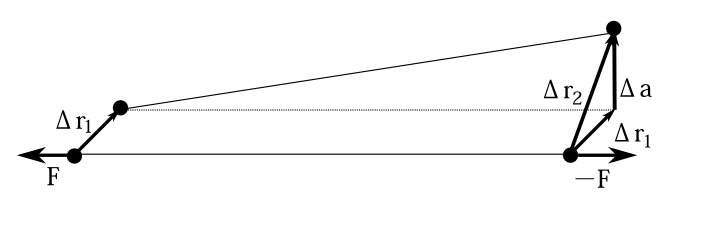
図2-2 2点間の距離を一定に拘束する力は仕事をしない。
今、2つの質点の距離が変わらないという拘束条件があるとしよう。2つの質点が堅い棒で結ばれているような場合である。2つの質点が互いに及ぼす力は向きが反対で大きさは等しい。力の方向は質点を結ぶ直線上である。この内力が可能な変位に対して仕事をしないことを示そう。 図2-2のように一方の質点の微小変位を\(\Delta \mathbf{r}_1\)、もう一方の質点の微小変位を\(\Delta \mathbf{r}_2\)とする。\(\Delta \mathbf{r}_2\)を \[ \Delta \mathbf{r}_2=\Delta \mathbf{r}_1+\Delta \mathbf{a} \] と分解しよう。すなわち、質点1の微小変位とそれ以外に分けるのである。質点1にかかる内力を\(\mathbf{F}\)とすると質点2にかかる内力は\(-\mathbf{F}\)である。可能な微小変位に対する仕事は \[ \mathbf{F}\cdot\Delta \mathbf{r}_1-\mathbf{F}\cdot(\Delta \mathbf{r}_1+\Delta\mathbf{a})=-\mathbf{F}\cdot \Delta\mathbf{a} \] である。\(\Delta \mathbf{a}\)は質点1を固定して質点2を、2つの質点の距離を一定のまま動かすわけだから(図2-2参照)、2つの質点を結ぶ線に直交する。すなわち\(\mathbf{F}\)と直交する。よって内力は可能な変位に対して仕事をしない。 だから、ラグランジュ方程式では、2つの質点間の力は一般化力に入れなくてよい。このことは応用性が高い。剛体は質点間の距離が変わらない。だから剛体の内力は一般化力に入れなくてよい。
1次元で2点間の距離が一定という拘束力があり、それ以外の力がないとき、この拘束力は仕事をしないのでラグランジュ方程式として式(\ref{lah4})が使える。相対・重心座標でのラグランジアンは式(\ref{lb5})の\(\dot{x}_s=0\)の場合で \[ L=\frac{1}{2}(m_1+m_2){\dot{x}_g}^2 \] である。だからラグランジュ方程式は \[ (m_1+m_2)\ddot{x}_g=0 \] となる。【例終】
2-6節 ラグランジアンの定義再考、時間を含むラグランジアン
この節では少し細かい話をするので飛ばしてもらっても一向に差し支えない。 今までラグランジアンを\(T-V\)だと安易に定義してきた。それは正しいのだが、少しそのことを反省してみよう。ラグランジアンの構成要素の運動エネルギー\(T\)についてまず考えよう。ある瞬間の運動エネルギーというのは慣性系ごとに値が異なる。例えばある慣性系で粒子が静止していたとすると運動エネルギーは0だが、その慣性系に対して速度\(u\)で等速運動している慣性系から見れば、その粒子の運動エネルギーは\(\frac{1}{2}mu^2\)である。 次にもう一つのラグランジアンの構成要素であるポテンシャル\(V\)について考えよう。ある粒子のある瞬間でのポテンシャルというのはどの座標系でも同じである。これは同じというよりもポテンシャルというものは定義からして同じものなのである。そういうわけで、ラグランジアンというのは慣性系ごとに異なる値を持つ。だからラグランジアンというものは、どの慣性系の運動エネルギーを採用しているかにも言及しなければならない。しかし通常はそんなことは全く気にしなくて良い。それは基本的にはその座標が張り付いている慣性系の運動エネルギーを採用すればよいからである。
次に時間を含むラグランジアンというものについて述べよう。まず運動エネルギーについてまず考えよう。簡単のために1次元で考える。慣性系に張り付いた単位座標で運動エネルギーは \(\frac{1}{2}m\dot{x}^2\)である。この座標に対して \[ x'=x+t^2 \] というように変換すると、速度の変換は \[ \dot{x}'=\dot{x}+2t \] となる。速度の変換も時間を含むことになり、運動エネルギーはこの座標系で表すと\(\frac{1}{2}m(\dot{x}'-2t)^2\)と、時間を含むことになる。慣性系に固定された単位座標との座標変換で時間を含むと必ず運動エネルギーに時間を含むようになるかというと、そんなことはない。要は速度の変換に時間を含むかどうかである。例えばその\(x\)系に対して速度\(u\)で等速直線運動している慣性系\(x'\)系との座標変換は \[ x'=x-ut \] であり、速度の変換は \[ \dot{x}'=\dot{x}-u \] である。速度の変換に時間を含んでいない。だから運動エネルギーは \[ T=\frac{1}{2}m(\dot{x}'+u)^2 \] となり時間を含まない。だから
慣性系の直交座標では、運動エネルギーとしてどの慣性系での運動エネルギーを採用しようとも時間を含まない。
今まで直交座標という言葉を安易に使ってきたが、直交座標とは慣性系に固定された直交する棒で長さを測った座標系のことである。慣性系と直交座標は同一視する場合もあるがここでは意味は異なる。詳細な議論はしないが、ここでの慣性系は架空の剛体とでも考えてもらいたい。直交座標との変換で時間を含まな い座標変換なら、その座標系で運動エネルギーは時間を含まない。時間を含まない座標変換というのは要するにある座標値間の対応関係が時間によらないということである。ある座標値が3でそれが6に変換されるなら、その1秒後も座標3は6に変換されるという意味である。物理的に言えば、直交座標と時間を含まない変換で結ばれた座標系とは、直交座標に固定された座標系とい言うことである。直交座標は慣性系に固定された座標系なので、直交座標と時間を含まない変換で結ばれた座標系とは、慣性系に固定された座標系のことである。だから
慣性系に固定された座標系では、運動エネルギーとしてどの慣性系での運動エネルギーを採用しようとも時間を含まない。
一方ポテンシャルに時間を含むかどうかだが、 ポテンシャルが時間を含まない座標(ポテンシャルを定義した座標系という意味だが)との変換が時間を含むときは、その座標系では必ずポテンシャルは時間を含むことになる。例えば調和振動子ポテンシャル \[ V=\frac{1}{2}kx^2 \] があるとしよう。この系に対して速度\(u\)で等速直線運動している慣性系の単位座標とは \[ x'=x-ut \] と変換する。するとこの座標を使うとポテンシャルは \[ V=\frac{1}{2}k(x'+ut)^2 \] というように必ず時間を含むことになる。
まとめると、まずラグランジアンは慣性系ごとに値が異なるということ。しかし通常どの慣性系での運動エネルギーを使うかは、最も式が簡単なものを採用するに決まっているので気にしなくて良い。次に時間を含むラグランジアンについてだが、 運動エネルギーは慣性系に固定された座標系ではどの慣性系の運動エネルギーを採用しようとも時間を含まない。時間を含むのは速度の変換に時間を含む場合である。ポテンシャルについては、座標変換に時間を含む場合は、ポテンシャルに時間を含むことになる。通常、座標変換に時間を含むような特殊な座標系など考えることはない。だから時間を含むラグランジアンなど考える必要は全くない。だから、今後の説明ではラグランジアンに時間を含んでいても通用するような議論をするのだが、ラグランジアンに時間など含んでないと思って読んでもらえば良い。
2-7節 ラグランジュ方程式と直交座標でのニュートンの運動方程式との同値性
ラグランジュ方程式 が、これを作る元になった直交座標の\(3n\)個の式 \begin{equation} m_i\ddot{x}_i=F_i\qquad i=1,2\cdots 3n \label{tyoc} \end{equation} と同値であるかについて簡単にふれたい。 それにはラグランジュ方程式と同値である \begin{equation} \frac{\partial\, x_i}{\partial\, q_\alpha}m_i\ddot{x}_i=\frac{\partial\, x_i}{\partial\, q_\alpha}F_i \label{lahc} \end{equation} との同値性を考えれば良い。 もし拘束条件がないなら、すなわち一般座標でも自由度が直交座標のそれと等しいなら、式(\ref{lahc})の両辺に\(\frac{\partial\, q_\alpha}{\partial\, x_j}\)を掛けて\(\alpha\)で和をとれば式(\ref{tyoc})に戻るわけだから、明らかに同値である。拘束条件がある場合は少しややこしい。拘束力というのは未定だから何をもって同値かというのが難しいのである。それで常識的に考えてみよう。拘束条件が例えば2つなら、\(q_\alpha\)系の自由度は\(3n-2\)となり、ラグランジュ方程式(\ref{lahc})の数も\(3n-2\)個できるわけである。この場合\(3n-2\)個の変数に対し、\(3n-2\)個の微分方程式があるわけだから、初期条件を決めてやれば、\(q_\alpha\)は時間の関数として決まるだろう。だから運動は完全に決まるわけである。そしてそれを使って\(\ddot{x}_i\)を求めることができ、それを使って式(\ref{tyoc})から\(F_i\)の値も求まるであろう。そういう意味でラグランジュ方程式(\ref{lahc})は直交座標の運動方程式(\ref{tyoc})と同値だと考えていいであろう。
2-8節 まとめ
ラグランジュ方程式というのは、直交座標でのニュートンの運動方程式である \[ m_i\ddot{x}_i=F_i \] の両辺に\(\frac{\partial\, x_i}{\partial\, q_\alpha}\)を掛けて指標\(i\)について和をとった \begin{equation} \sum_i\frac{\partial\, x_i}{\partial\, q_\alpha}m_i\ddot{x}_i=\sum_i\frac{\partial\, x_i}{\partial\, q_\alpha}F_i \label{lahd} \end{equation} という式を、他の式に置き換えたものである。この式は行列で書くと \[ \left( \begin{array}{ccc} \frac{\partial\, x_1}{\partial\, q_1}&\frac{\partial\, x_2}{\partial\, q_1}&\cdots\\ \frac{\partial\, x_1}{\partial\, q_2}&\frac{\partial\, x_2}{\partial\, q_2}&\cdots\\ \cdots&\cdots&\cdots\\ \end{array} \right) \left( \begin{array}{c} m_1 \ddot{x}_1\\ m_2 \ddot{x}_2\\ \cdots\\ \end{array} \right) = \left( \begin{array}{ccc} \frac{\partial\, x_1}{\partial\, q_1}&\frac{\partial\, x_2}{\partial\, q_1}&\cdots\\ \frac{\partial\, x_1}{\partial\, q_2}&\frac{\partial\, x_2}{\partial\, q_2}&\cdots\\ \cdots&\cdots&\cdots\\ \end{array} \right) \left( \begin{array}{c} F_1\\ F_2\\ \cdots\\ \end{array} \right) \] である。\(q,\dot{q},\ddot{q}\)系についての恒等式 \[ \sum_i\frac{\partial\, x_i}{\partial\, q_\alpha}m_i\ddot{x}_i = \frac{d}{dt}\left(\frac{\partial\, T}{\partial\, \dot{q}_\alpha}\right)-\frac{\partial\, T}{\partial\, {q}_\alpha} \] と 一般化力の定義 \[ f_\alpha\equiv \sum_i\frac{\partial\, x_i}{\partial\, q_\alpha}F_i \] を使うと式(\ref{lahd})は \begin{equation} \frac{d}{dt}\left(\frac{\partial\, T}{\partial\, \dot{q}_\alpha}\right)-\frac{\partial\, T}{\partial\, {q}_\alpha}=f_\alpha \label{lah2c} \end{equation} と書き換えられる。これは単に式(\ref{lahd})を別の記号で置き換えただけであり、何の物理的内容も追加していない。この式をラグランジュ方程式という。一般化力\(f_\alpha\)というのは\(q_\alpha\)の単位変化あたりの仕事量のことである。もし条件1(2-4節参照)が満たされるなら、すなわち力が、ポテンシャル\(V\)からの力と仕事をしない力以外は含まないときは、一般化力は \[ f_\alpha=-\frac{\partial\, V}{\partial\, q_\alpha} \] となり、ラグランジアン\(L\equiv T-V\)を使うと、 式(\ref{lah2c})は \begin{equation} \frac{d}{dt}\left(\frac{\partial\, L}{\partial\, \dot{q}_\alpha}\right)=\frac{\partial\, L}{\partial\, {q}_\alpha} \label{lah4c} \end{equation} と書き換えられる。直交座標での運動方程式 \(m_i\ddot{x}_i=F_i\)に \(\frac{\partial\, x_i}{\partial\, q_\alpha}\)を掛けて\(i\)で和をとっているのは、条件1を満たせばラグランジュ方程式(\ref{lah2c})の右辺が\(f_\alpha=-\frac{\partial\, V}{\partial\, q_\alpha}\)と簡単になるからである。まとめると式(\ref{lahd})を\(q_\alpha\)座標系で表したものがラグランジュ方程式であり、それを書き換えたものが式(\ref{lah2c})であり、状況が特別な場合はそれは式(\ref{lah4c})とも書けるということである。