第7章 変分法とハミルトンの原理1
この章では解析力学と変分法の関係について述べたい。どういう関係かというと、簡単に言えば、力学の法則を満たす軌道はラグランジアンの時間積分の停留関数となるということ(ハミルトンの原理)である。これは単なる数学的事実である。そんなことを知ったからと言って、物理をより深く理解できるようになるということは全くないだろう。ただファインマンの経路積分の考えの理解には役立つと思う。解析力学の方程式を導出するのに変分法は必要なかったことは今までに示したことである。 後半では力学の法則を満たす軌道は最小関数になるのかを考察した。この部分は興味のある人だけ読めばいいと思う。後の章で使うこともない。7-3節と7-4節は脱線した話なので飛ばしてもらえば良い。
7-1節 変分法について
まず簡単に変分法というものについて述べよう。\(x(t)\)を時間の関数とする。\(x\)と\(\dot{x}\)と\(t\)の関数\(f(x,\dot{x},t)\)が与えられているとしよう。例えばラグランジアン\(L=\frac{1}{2}m\dot{x}^2-V(x)\)は\(x\)と\(\dot{x}\)の関数なので、そういう関数の1つである。さて \begin{equation} I[x(t)]\equiv\int_{t_a}^{t_b} f(x(t),\dot{x}(t),t)dt \label{toumen} \end{equation} という積分は\(x(t)\)を変化させれば、その積分値がかわる。だからこの積分は、時間の関数\(x(t)\)の関数である。それで左辺を\(I[x(t)]\)と書いたのである。これは関数の関数だから汎関数という。\(x(t)\)を変関数と呼ぶことにしよう。ここでの主題というのは\(x(t)\)を、積分区間の両端では変化させないという条件のもとで、図7-1のように微小量\(\delta x\)だけ変化させたとき、その微小量の1次の範囲では、この積分値が変化しないという\(x(t)\)を探すことである。このような関数\(x(t)\)を停留関数と呼ぼう。
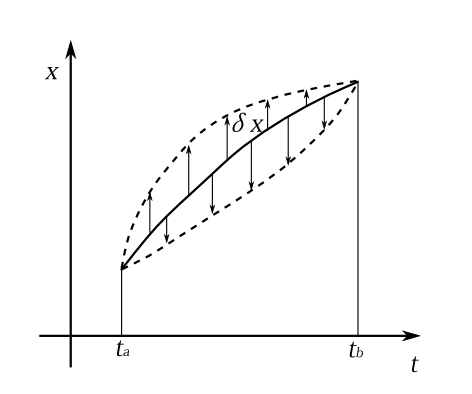
図7-1 始点\(t_a\)と終点\(t_b\)では\(x\)の値を固定して、\(x\)を変化させる。
それで\(x(t)\)が停留関数となるための必要十分条件を見つけよう。 \begin{eqnarray} I[x+\delta x]-I[x]&=&\int_{t_a}^{t_b} f(x+\delta x,\dot{x}+\delta \dot{x},t)dt-\int_{t_a}^{t_b} f(x(t),\dot{x}(t),t)dt\notag\\ &=&\int_{t_a}^{t_b} f(x+\delta x,\dot{x}+\delta \dot{x},t)-f(x(t),\dot{x}(t),t)\; dt\notag \end{eqnarray} そして\(\delta x\)と\(\delta \dot{x}\)の1次の範囲では \[ I[x+\delta x]-I[x]\cong \int_{t_a}^{t_b}\left(\frac{\partial\, f}{\partial\, x}\delta x+\frac{\partial\, f}{\partial\, \dot{x}} \delta \dot{x}\right)dt \] である。 部分積分により \[ \int_{t_a}^{t_b}\frac{\partial\, f}{\partial\, \dot{x}} \delta \dot{x}dt= \left[\frac{\partial\, f}{\partial\, \dot{x}}\delta x\right]_{t_a}^{t_b} -\int_{t_a}^{t_b}\frac{d}{dt}\left(\frac{\partial\, f}{\partial\, \dot{x}}\right)\delta x dt \] となる。\(\delta x\)は積分区間の両端で\(0\)なので第1項は\(0\)である。だから \begin{equation} I[x+\delta x]-I[x]\cong \int_{t_a}^{t_b}\left[\frac{\partial\, f}{\partial\, x}-\frac{d}{dt}\left(\frac{\partial\, f}{\partial\, \dot{x}}\right)\right]\delta x\; dt \label{he3} \end{equation} となる。\(x(t)\)が停留関数となるための必要十分条件は \begin{equation} \int_{t_a}^{t_b}\left[\frac{\partial\, f}{\partial\, x}-\frac{d}{dt}\left(\frac{\partial\, f}{\partial\, \dot{x}}\right)\right]\delta x\; dt \label{he4} \end{equation} が、任意の\(\delta x\)で\(0\)となることである。そうなるためには \[ \frac{\partial\, f}{\partial\, x}-\frac{d}{dt}\left(\frac{\partial\, f}{\partial\, \dot{x}}\right) \] がこの区間で常に\(0\)であればもちろんよいが、もし、\(0\)とならない区間があったとしたら 、これを\(a(t)\)と置いて、 \(\epsilon\)をただの定数として、\(\delta x=\epsilon a(t)\)とすれば式(\ref{he4})は \[ \epsilon\int_{t_a}^{t_b}a(t)^2\; dt\ne 0 \] となってしまう。だから\(a(t)\)は常に\(0\)でなければならない。すなわち
定理7-1 \(x(t)\)が汎関数 \[ I[x(t)]=\int_{t_a}^{t_b} f(x(t),\dot{x}(t),t)dt \] の停留関数となるための必要十分条件は\(f\)に対する\(x\)のオイラーの方程式 \begin{equation} \frac{d}{dt}\left(\frac{\partial\, f}{\partial\, \dot{x}}\right)=\frac{\partial\, f}{\partial\, x} \label{he5} \end{equation} をこの積分区間で満たすことである。
今、停留の定義を汎関数\(I[x(t)]\)の\(\delta x,\delta\dot{x}\)の1次までの変化量が\(0\)であることとしていた。これをもう少し厳密にすると、次のようなことが停留の定義でいいと思う。\(\delta x,\delta\dot{x}\)の積分区間での最大値が\(0\)に近づくとき、\(I[x+\delta x]-I[x]\)がそれより速く\(0\)に収束すること。数学的記号を使うと、\(\delta x,\delta\dot{x}\)のうち積分区間内での最大値を\(M\)とすると \[ \lim_{M\to 0}\frac{I[x+\delta x]-I[x]}{M}=0 \] となること。私は数学者でもなく、この分野の現代的な数学書も読んだことはないが、これが停留の定義でいいと思う。
今の定義での停留のための必要十分条件がオイラーの方程式(\ref{he5})を満たすことである、ということは当然変わらないであろう。ただその証明は難しいことではないと思うのだが、技術的でつまならい細かさがありそうなのでやめておくことにする。
7-2節 変関数が2つ以上のとき
今は汎関数\(I[x(t)]\)の変換数として1つの場合を扱ったが、次に変関数が\(x(t),y(t)\)と2つの場合を考えよう。すなわち汎関数 \begin{equation} I[x(t),y(t)]=\int_{t_a}^{t_b} f\big(x(t),\dot{x}(t),y(t),\dot{y}(t),t\big)dt \label{hen1} \end{equation} の停留関数を考えるのである。2変数関数のときの停留関数の意味も、1変関数のときと同じで\(x(t),y(t)\)を積分区間の両端で変化させないという条件で変化させ、その変化量の1次の範囲では\(I[x,y]\)が変化しないときに、その\(x(t),y(t)\)を停留関数と呼ぶのである。このときも1変関数のときと同様に考えれば、停留のための必要十分条件が1変関数のときと同じであることは明らかであろう。すなわち汎関数(\ref{hen1})で\(x(t),y(t)\)が停留関数であるための必要十分条件は積分区間内で、\(f\)に対して\(x(t),y(t)\)共にオイラーの方程式 \[ \frac{d}{dt}\left(\frac{\partial\, f}{\partial\, \dot{x}}\right)=\frac{\partial\, f}{\partial\, x} \qquad\qquad \frac{d}{dt}\left(\frac{\partial\, f}{\partial\, \dot{y}}\right)=\frac{\partial\, f}{\partial\, y} \] を満たすことである。これは変関数が何個あっても同じであり、いつものようにそれぞれの変関数を指標で分類して \(x_i(t)\)とかくと
定理7-2 汎関数 \[ I[x_i(t)]=\int_{t_a}^{t_b} f\big(x_i(t),\dot{x}_i(t),t\big)dt \] で\(x_i(t)\)が停留関数となるための必要十分条件はすべての\(x_i\)がこの積分区間で\(f\)に対してオイラーの \[ \frac{d}{dt}\left(\frac{\partial\, f}{\partial\, \dot{x}_i}\right)=\frac{\partial\, f}{\partial\, x_i} \] を満たすことである。
といえる。
7-3節 時間で全微分した関数がオイラーの方程式をみたすことの変分法的意味
少し、脱線した話をするのでこの節は飛ばしてもらって良い。
さて、定理1-1の等式4で任意の関数\(f(x_i(t),t)\)の時間での全微分\(\frac{df}{dt}\)は任意の\(x_i(t)\)についてオイラーの方程式を満たすということを述べた。このことを変分法との関係で見てみよう。今汎関数 \[ I[x_i(t)]=\int_{t_a}^{t_b} \frac{d}{dt}f(x_i(t),t)dt \] の停留関数を考える。この積分は \[ I[x_i(t)]=f(x_i(t_b),t_b)-f(x_i(t_a),t_a) \] である。すなわち、この汎関数は\(x_i(t)\)の積分区間の両端の値で決まってしまい、積分区間内で\(x_i\)を変化させても汎関数\(I[x_i(t)]\)は変化しない。すなわち、任意の\(x_i(t)\)が停留関数になるということである。\(x_i(t)\)が停留関数ならばオイラーの方程式 \[ \frac{d}{dt}\left(\frac{\partial\, \dot{f}}{\partial\, \dot{x}}\right)=\frac{\partial\, \dot{f}}{\partial\, x} \] を満たすということである。このことは任意の関数\(f(x_i,t)\)に言えることである。このように\(x_i(t),f(x_i,t)\)がどんな関数であろうとも、\(x_i\)が\(\dot{f}\)に対してオイラーの方程式を満たすことが変分法の方法でも証明できたわけである。
7-4節 変分法を多変数関数として考える
ここも少し脱線した話なので飛ばしてもらって良い。
変分法というのは少しわかりづらいかもしれない。そこで変分法を多変数関数の微分と考え、変数の個数が無限に多くなる極限が変分問題であるとして扱ってみよう。簡潔なため、1変関数の変分 \begin{equation} I[x(t)]=\int_{t_a}^{t_b} f(x(t),\dot{x}(t),t)dt \label{henbu1} \end{equation} を考える。
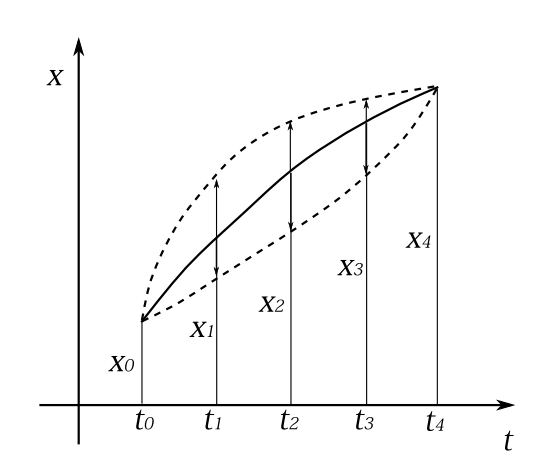
図7-2
積分区間を図7-2のように\(\Delta t\)ごとに\(n\)等分し(図7-2では4等分している)、始点を\(t_0\)とし、\(\Delta t\)増えるごとに\(t_1,t_2,\cdots\)として終点を\(t_n\)とする。そして \[ x_m\equiv x(t_m),\qquad \dot{x}_m\equiv \frac{x_{m+1}-x_m}{\Delta t},\qquad f_m\equiv f(x_m,\dot{x}_m,t) \] と書くことにする。式(\ref{henbu1})の右辺 をこの記号を使って離散的に書くと \[ \sum_{m=0}^{n-1}f_m \Delta t \] となる。これを\(\Delta t\to 0\)とした極限が式(\ref{henbu1})の右辺である。ここでは\(x_1,x_2\cdots, x_{n-1}\)を変数と考える。\(x_1,x_2\cdots,x_{n-1}\)が停留点であるため必要十分条件は \[ \frac{\partial\,}{\partial\, x_m}\sum_{j=0}^{n-1}f_j \Delta t=0\qquad\qquad(m=1,2,\cdots,n-1) \] である。これは \[ \frac{\partial\, f_m}{\partial\, x_m}+\frac{\partial\, \dot{x}_m}{\partial\, x_m}\frac{\partial\, f_m}{\partial\, \dot{x}_m}+\frac{\partial\, \dot{x}_{m-1}}{\partial\, x_m}\frac{\partial\, f_{m-1}}{\partial\, \dot{x}_{m-1}}=0 \] ということであり、 \[ \frac{\partial\, \dot{x}_m}{\partial\, x_m}=-\frac{1}{\Delta t} \qquad\qquad \frac{\partial\, \dot{x}_{m-1}}{\partial\, x_m}=\frac{1}{\Delta t} \] なので \[ \frac{\partial\, f_m}{\partial\, x_m}-\frac{1}{\Delta t}\left(\frac{\partial\, f_m}{\partial\, \dot{x}_m}-\frac{\partial\, f_{m-1}}{\partial\, \dot{x}_{m-1}}\right) =0 \] となる。これがすべての\(x_m\)で で成り立つことが停留点となるための必要十分条件である。ここで\(\Delta t\to 0\)の極限とすれば \[ \frac{\partial\, f}{\partial\, x}-\frac{d}{dt}\left(\frac{\partial\, f}{\partial\, \dot{x}}\right)=0 \] というオイラーの方程式が得られる。このように時間の関数\(x(t)\)を離散的に捉えて、汎関数\(I[x(t)]\)をただの多変数関数として考えるのは、わかりやすいし、数値計算で停留関数を求めるのにも有用であろう。
7-5節 停留関数の変数変換
汎関数の停留関数というのは変数変換しても、停留関数になる。これはどういうことかというと、例えば1変関数\(x(t)\)が汎関数 \begin{equation} I[x(t)]=\int_{t_a}^{t_b} f(x(t),\dot{x}(t),t)dt \label{h91} \end{equation} での停留関数ならば、\(x'(t)=2x(t)\)という関数も不変量としての\(I[x]\)の停留関数になるだろう。すなわち\(x=\frac{x'}{2}\)なので、これを式(\ref{h91})に代入して \[ I[x'/2]=\int_{t_a}^{t_b} f(x'(t)/2,\dot{x}(t)/2,t)dt \] という汎関数を作り、\(x'\)がこの汎関数の停留関数になるということである。今のような線形な変換でなく、\(x'=x^2\)というような変換でも\(x'\)は汎関数(\ref{h91})の停留関数になろう。さらには、変関数が2つ以上、例えば\(x(t),y(t)\)とあって、\(x(t),y(t)\)が汎関数 \begin{equation} I[x(t),y(t)]=\int_{t_a}^{t_b} f(x(t),\dot{x}(t),y(t),\dot{y}(t),t)dt \label{h92} \end{equation} の停留関数だとしたら \begin{equation} x'=x'(x,y,t), \qquad\qquad y'=y'(x,y,t) \label{h93} \end{equation} という変換をすれば、\(x'(t),y'(t)\)も汎関数(\ref{h92})の停留関数になろう。すなわち変換(\ref{h93})を逆に解いた \(x=x(x',y',t),\;y=y(x',y',t)\)を式(\ref{h92})に代入した汎関数 \[ I[x(x',y',t),y(x',y',t)]=\int_{t_a}^{t_b} f(x(x',y',t),\dot{x}(x',y',t),y(x',y',t),\dot{y}(x',y',t),t)dt \] を考えた場合、\(x',y'\)はこの汎関数の停留関数になろう。一般に
定理7-3 \(x_i(t)\)が \begin{equation} I[x_i(t)]=\int_{t_a}^{t_b} f(x_i(t),\dot{x}_i(t),t)dt \label{h94} \end{equation} の停留関数ならば\(x_i\)を変数変換した\(x'_k=x'_k(x_i,t)\) もこの汎関数の停留関数となる。
と言える。これをオイラーの方程式の不変性から証明しよう。
【証明】\(x_i(t)\)が汎関数(\ref{h94})の停留関数ならば、すべての\(x_i(t)\)について、オイラーの方程式
\[
\frac{d}{dt}\left(\frac{\partial\, f}{\partial\, \dot{x}_i}\right)-\frac{\partial\, f}{\partial\, x_i}=0
\]
を満たす。
ところで第1章定理1-3で述べたように\(x_i(t)\)がオイラーの方程式を満たすなら、それを変数変換した\(x'_k=x'_k(x_i,t)\)も不変量としての\(f\)に対してオイラーの方程式を満たす。オイラーの方程式を満たすことと停留関数であることは同値であった(定理7-2)。よって\(x'_k(t)\)は汎関数(\ref{h94})の停留関数となる。【証明終】
定理7-3は停留の意味を考えれば、当然予想される結果である。汎関数\(I[x]\)は\(x_i\)がわずかに変化しても変化しないわけである。ところで\(x\)と\(x'\)は\(x'=x'(x,t)\)という連続関数で結ばれているわけだから
\(\delta x\)は\(\delta x'\)に比例し、\(\delta \dot{x}\)は\(\delta \dot{x}'\)に比例する。だから
\(x'\)がわずかに動いても\(x\)もわずかしか動かない。よって汎関数は変化しないというわけである。
7-6節 ラグランジアンの停留関数
ハミルトンの原理
ようやく準備もできたので、この節では変分法と解析力学の関わりについて述べる。力学の法則を満たす軌道\(q_i(t)\)というのはラグランジアン\(L(q,\dot{q},t)\)についてのオイラーの方程式 \[ \frac{d}{dt}\left(\frac{\partial\, L}{\partial\, \dot{q}_i}\right)-\frac{\partial\, L}{\partial\, q_i}=0 \] を満たすのであった。ということは
定理7-4 ハミルトンの原理 力学の法則を満たす軌道\(q_i(t)\)というのは汎関数 \begin{equation} I[q(t)]=\int_{t_a}^{t_b} L(q(t),\dot{q}(t),t)dt \label{h111} \end{equation} の停留関数である
ということである。このことをハミルトンの原理という。力学の法則を満たす軌道が停留関数であるという事実を知ったからと言って、何か力学についての知見が得られるわけではない。しかしながら、ファインマンの経路積分では、この事実を使って古典力学と量子力学のつながりを説明している。
もう一つの変分問題
今の程はポピュラーではないが、もう1つ似たようなものを述べよう。力学の法則を満たす軌道と運動量\(q(t),p(t)\)というのは \[ \mathcal{L}(q,\dot{q},p,t) \equiv \sum_ip_i\dot{q}_i-H(q,p,t) \] に対してオイラーの方程式を満たすのであった(5章定理5-5)。左辺を\(\mathcal{L}(q,\dot{q},p,t)\)と書いたのはもし \[ p_i=\frac{\partial\, L(q,\dot{q},t)}{\partial\, \dot{q}_i} \] を満たすならば右辺はラグランジアンと等しいからである。さて、オイラーの方程式を満たすということは力学の法則を満たす\(q(t),p(t)\)は汎関数 \begin{equation} I[q(t),p(t)]=\int _{t_a}^{t_b}\sum_i p_i\dot{q}_i-H(q,p,t)\;dt \label{h112} \end{equation} の停留関数であるということである。注意としては、この変分問題は、ラグランジアン\(L\)を\(q,\dot{q},t\)で表した変分問題とは全く異なるということである。汎関数(\ref{h111})の変分問題は\(q\)を自由に動かしての停留問題であった。今の汎関数(\ref{h112})は\(q\)も\(p\)も独立に自由に動かしての停留問題だということである。しかし実際の空間上の軌道ならば\(q\)を変化させれば、それに応じて\(p\)も変化するはずである。例えば直交座標なら\(p_i=m\dot{q}_i\)という関係があり、\(q\)が変化すれば\(\dot{q}\)が変化して、そして\(p\)も変化するはずである。それなのに\(q\)も\(p\)も独立の変関数として扱うということは、この変分問題は物理的な空間上の軌道の変分問題ではなく、数学上の\(q,p\)空間での、無理やり作ったような変分問題なのである。
7-7節 変分問題の最小性、極小性1
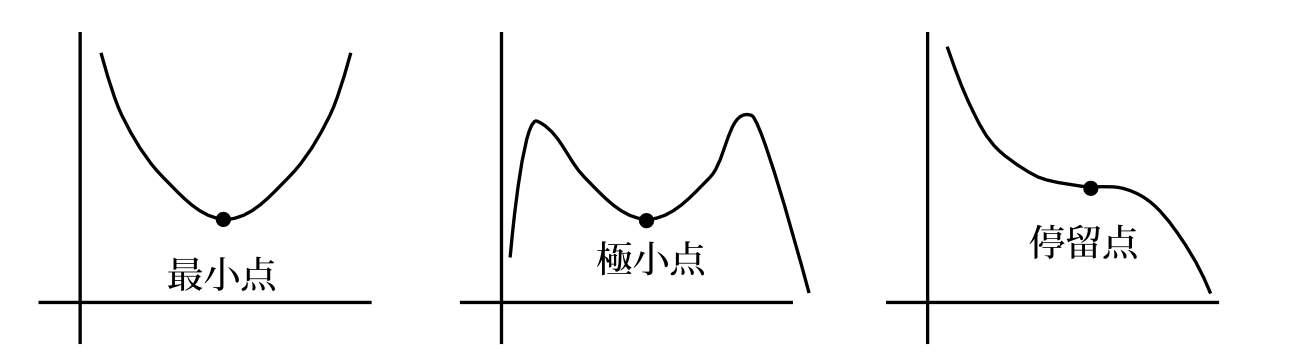
図7-3 関数での最小点、極小点、停留点。汎関数での最小関数、極小関数、停留関数の意味もこれからの類推で想像できよう。
さて、力学の法則を満たす軌道というのは \begin{equation} I[q(t)]=\int_{t_a}^{t_b} L(q(t),\dot{q}(t),t)dt \label{h131} \end{equation} の停留関数であった。このことを最小作用の原理と呼んでいる文献もある。例えばファインマンの本がそうである。次の第8章で述べる変分問題を最小作用の原理と読んでいる本もある。どちらかというとそういう本の方が多いような気がする。ところで力学の法則を満たす軌道というのは汎関数(\ref{h131})を最小にするのであろうか、又は極小にするのか、はたまた、最小でもなく、極小でもないのか、ということは興味あることである。それでそのことを調べようというわけである。微分法の「最小値」、「極小値」からの類推で想像はつくと思うが一応、最小関数と極小関数というものも定義しておこう(図7-3)。ある関数\(x(t)\)を積分区間の両端を固定した上で変化させたとき、汎関数 \[ I[x(t)]\equiv\int_{t_a}^{t_b} f(x(t),\dot{x}(t),t)dt \] の値が必ず大きくなるなら、その関数\(x(t)\)を最小関数と呼ぼう。ある関数\(x(t)\)を積分区間の両端を固定した上で微小量\(\delta x\)だけ変化させたとき、この汎関数が必ず大きくなるなら、その関数\(x(t)\)を極小関数と呼ぼう。
1次元自由粒子
まず一番簡単な1次元自由粒子について調べよう。この場合の汎関数は \begin{equation} I[x]=\int_{t_a}^{t_b}\frac{1}{2}m\dot{x}^2 dt \label{h130} \end{equation} である。\(\delta x(t)\)を積分区間の両端で\(0\)となる\(t\)の関数とする。この章では以後その意味で使うとする。変関数として\(x(t)+\delta x(t)\)を使うと \begin{eqnarray} I[x+\delta x]&=&\int_{t_a}^{t_b}\frac{1}{2}m(\dot{x}+\delta \dot{x})^2 dt\notag\\ &=&\int_{t_a}^{t_b}\left(\frac{1}{2}m\dot{x}^2+m\dot{x}\delta\dot{x}+\frac{1}{2}m\delta \dot{x}^2\right) dt\notag \end{eqnarray} となる。\(\int_{t_a}^{t_b}m\dot{x}\delta\dot{x} \;dt\)を部分積分すると \[ \int_{t_a}^{t_b}m\dot{x}\delta\dot{x} \;dt= [m\dot{x}\delta x]_{t_a}^{t_b}-\int_{t_a}^{t_b}m\ddot{x}\delta x\; dt \] となる。 \(\delta x\)は積分区間の両端で\(0\)なので第1項は0である。だから \begin{equation} \int_{t_a}^{t_b}\frac{1}{2}m(\dot{x}+\delta \dot{x})^2 dt= \int_{t_a}^{t_b}\left(\frac{1}{2}m\dot{x}^2-m\ddot{x}\delta x+\frac{1}{2}m\delta \dot{x}^2\right) dt \label{h133} \end{equation} となる。この式は後でも使う。\(x(t)\)を力学の法則を満たす軌道とすると\(\ddot{x}=0\)なので \[ I[x+\delta x]=I[x]+\int_{t_a}^{t_b}\frac{1}{2}m\delta \dot{x}^2 dt \] となる。第2項は任意の\(\delta x\)で\(0\)以上となる。だから\(x(t)\)を力学の法則を満たす軌道とすると、任意の変分\(\delta x\)に対して \[ I[x+\delta x]\ge I[x] \] となる。すなわちポテンシャルのないときは力学の法則を満たす軌道は、汎関数(\ref{h130})の最小関数である。
1次元自由落下
次に簡単な1次元自由落下の場合を考えよう。\(x\)軸の正の向きを落下方向にとると、ポテンシャルは\(-mgx\)なので汎関数は \begin{equation} I[x]=\int_{t_a}^{t_b}\frac{1}{2}m\dot{x}^2+mgx \;dt \label{h134} \end{equation} である。変関数を\(x+\delta x\)とすると \[ I[x+\delta x]=\int_{t_a}^{t_b}\frac{1}{2}m(\dot{x}+\delta \dot{x})^2+mg(x+\delta x) \;dt \] である。式(\ref{h133})の結果を使うと \[ I[x+\delta x]=I[x]+\int_{t_a}^{t_b}(-m\ddot{x}+mg)\delta x\;dt+\int_{t_a}^{t_b}\frac{1}{2}m\delta \dot{x}^2 dt \] となる。ここまでは任意の\(x(t)\)で成り立つ式なのだが、ここで\(x(t)\)を力学の法則を満たす軌道とすると\(\ddot{x}=g\)なので \[ I[x+\delta x]=I[x]+\int_{t_a}^{t_b}\frac{1}{2}m\delta \dot{x}^2 dt \] となる。ゆえに1次元自由粒子の場合と同じ理屈で、力学の法則を満たす軌道は汎関数(\ref{h134})の最小関数である。
1次元調和振動子
次に1次元調和振動子の場合を考えよう。この場合汎関数は \[ I[x]=\int_{t_a}^{t_b}\frac{1}{2}m\dot{x}^2-\frac{1}{2}m\omega^2 x^2 \;dt \] である。変関数を\(x+\delta x\)とすると \[ I[x+\delta x]=\int_{t_a}^{t_b}\frac{1}{2}m(\dot{x}+\delta \dot{x})^2-\frac{1}{2}m \omega^2 (x+\delta x)^2 \;dt \] である。式(\ref{h133})の結果を使うと \[ I[x+\delta x]=I[x]+\int_{t_a}^{t_b}(-m\ddot{x}-m \omega^2 x)\delta x\;dt+\frac{1}{2}m\int_{t_a}^{t_b}(\delta \dot{x}^2-\omega^2\delta x^2) dt \] となる。ここで\(x(t)\)を力学の法則を満たす軌道とすると\(\ddot{x}=-\omega^2 x\)なので \[ I[x+\delta x]=I[x]+\frac{1}{2}m\left(\int_{t_a}^{t_b}\delta \dot{x}^2 dt-\omega^2\int_{t_a}^{t_b}\delta x^2\; dt\right) \] となる。 だから任意の\(\delta x\)に対して \[ \int_{t_a}^{t_b}\delta \dot{x}^2 dt-\omega^2\int_{t_a}^{t_b}\delta x^2\; dt>0 \] となることが最小関数となるための必要十分条件である。 \(\int_{t_a}^{t_b}\delta \dot{x}^2 dt\)も\(\int_{t_a}^{t_b}\delta x^2\; dt\)も必ず正になるので、この不等式は \[ \frac{\int_{t_a}^{t_b}\delta \dot{x}^2 dt}{\int_{t_a}^{t_b}\delta x^2\; dt}>\omega^2 \] と同値である。 だから
\(\delta x\)をいろいろ変化させたときの \begin{equation} D[\delta x]\equiv\frac{\int_{t_a}^{t_b}\delta \dot{x}^2 dt}{\int_{t_a}^{t_b}\delta x^2\; dt} \label{ew2} \end{equation} が最も小さくなるときでも \begin{equation} \frac{\int_{t_a}^{t_b}\delta \dot{x}^2 dt}{\int_{t_a}^{t_b}\delta x^2\; dt}>\omega^2 \label{ew3} \end{equation} が成り立つことが最小関数になるための必要十分条件である
と言える。そしてこれが成り立たないことが、最小関数にならないための必要十分条件である。(\ref{ew2}) には最小値が存在するということは想像つくと思う。すなわち、\(\delta x\)を変化させたときに、いくらでも0に近づくことはないということである。とりあえず最小値があるとして、 それを\(D_{\text{min}}\)と書こう。だから\(D_\text{min} > \omega^2\)ならその軌道は最小関数になるし、これが成り立たないなら最小関数にならないのである。\(D_{\text{min}}\)の値は軌道の積分時間\(t_b-t_a\)にのみ依存している。だから与えられた\(t_b-t_a\)に対して\(\omega\)が十分大きければ\(D_\text{min} > \omega^2\)が成り立たない。そのような軌道は最小関数にならない。
もう少し詳しく述べよう。 まず\(D_{\text{min}}\)を与える\(\delta x\)を求めよう。これは \(\int_{t_a}^{t_b}\delta x^2\; dt\) が一定の条件、例えば\(\int_{t_a}^{t_b}\delta x^2\; dt=3\)という条件の中から\(\int_{t_a}^{t_b}\delta \dot{x}^2 dt\)が最小となる関数を求めるということと同じである。 というのは、もしある関数\(\delta x_\text{min}\)が\(D\)を最小にするなら、 すなわち\(D[\delta x_\text{min}]=D_\text{min}\)なら、この定数\(k\)倍の\(k\delta x_\text{min}\)も\(D\)を最小にする。 すなわち\(D[k\delta x_\text{min}]=D_\text{min}\)となる。\(k\)を適当にとれば\(\int_{t_a}^{t_b}k^2(\delta x_\text{min})^2\; dt\)は任意の正の値、例えば3という値をとることができる。だから\( \int_{t_a}^{t_b}\delta x^2\; dt \)が3という値をとるものの中から\(D[\delta x]\)が最小となるものを探せば十分なのである。そして\(D\)の分母が一定ならば、分子の\(\int_{t_a}^{t_b}\delta \dot{x}^2 dt\)が最小となる\(\delta x\)を探せばよいわけである。 そういうわけでこの方法で最小とする\(\delta x\)を探そう。それにはラグランジュの未定乗数法を使おう。それは \[ \int_{t_a}^{t_b}\delta \dot{x}^2 -\lambda \delta x^2\; dt \] という変分問題となる。ここで\(\lambda\)は未定定数。これに対するオイラーの方程式は \[ \frac{d}{dt}(2\delta \dot{x})=-\lambda (2\delta x) \] でありその解は \[ \delta x=A\cos \sqrt{\lambda} \;t+B\sin \sqrt{\lambda} \;t \] である。ここで\(A,B\)は積分定数。境界条件を考慮すると \(D[\delta x]\) を停留させるのは \[ \delta x=\sin\frac{\pi (t-t_a)}{t_b-t_a} \] のときである。この\(\delta x\)が\(D\)を最小にするとは証明できないが、おそらく最小にしているのであろう。そして、これを式(\ref{ew2})に入れると \[ D_\text{min}=\frac{\pi^2}{(t_b-t_a)^2} \] と求まる。 これを式(\ref{ew3})に入れると \begin{equation} \frac{\pi^2}{(t_b-t_a)^2}>\omega^2 \label{ew4} \end{equation} となる。この調和振動子ポテンシャルでの周期を\(T\)とすると\(2\pi/T=\omega\)なので、式(\ref{ew4})は \[ \frac{T}{2}>t_b-t_a \] となる。だから最小関数となるための必要十分条件は積分区間がポテンシャルによって決まる周期の半分より小さい時である。だから十分時間が短ければ最小関数になるし十分長ければ最小関数にならない。ポテンシャルだけでは最小関数になるかどうかは決まらず、積分時間との兼ね合いで決まるということである(図7-4)。
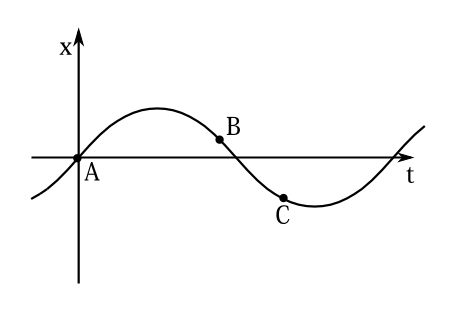
図7-4 始点A、終点Bの軌道は半周期より短いので最小関数になる。始点A、終点Cの軌道は半周期より長いので最小関数にならない。
1次元一般のポテンシャル
今まで1次元の自由粒子、自由落下、調和振動子での最小問題を論じてきた。自由粒子と自由落下では最小になる。調和振動子では最小になるかどうかは力の大きさと積分時間の兼ね合いである。次に、1次元の場合の一般のポテンシャルのときの極小問題を考えたい。 最小でなく、極小しか論じられないのは、汎関数を\(\delta x\)で展開する方法では最小かどうかについて何も結論を出せないからである。 ポテンシャル\(V(x)\)のときの汎関数は \[ I[x]=\int_{t_a}^{t_b}\frac{1}{2}m\dot{x}^2-V(x) \;dt \] である。変関数を\(x+\delta x\)とすると \begin{equation} I[x+\delta x]=\int_{t_a}^{t_b}\frac{1}{2}m(\dot{x}+\delta \dot{x})^2-V(x+\delta x) \;dt \label{h137} \end{equation} である。\(V(x+\delta x)\)は\(\delta x\)の2次まででは \[ V(x+\delta x)\cong V(x)+\frac{d V}{d x}\delta x+\frac{1}{2}\frac{d^2 V}{d x^2}\delta x^2 \] であり、これを式(\ref{h137})に入れ、式(\ref{h133})の結果を使うと \[ I[x+\delta x]\cong I[x]+\int_{t_a}^{t_b}\left(-m\ddot{x}-\frac{d V}{d x}\right)\delta x\;dt+\frac{1}{2}m\int_{t_a}^{t_b}\delta \dot{x}^2\; dt -\frac{1}{2}\int_{t_a}^{t_b}\frac{d^2 V}{d x^2}\delta x^2\; dt \] となる。\(x(t)\)を力学の法則を満たす軌道とすると、\(-m\ddot{x}-\frac{\partial\, V}{\partial\, x}=0\)なので第2項は消える。よって \[ I[x+\delta x]\cong I[x]+\frac{1}{2}m\int_{t_a}^{t_b}\delta \dot{x}^2\; dt -\frac{1}{2}\int_{t_a}^{t_b}\frac{d^2 V}{d x^2}\delta x^2\; dt \] となる。もし\(x(t)\)の軌道上で常に\(\frac{d^2 V}{d x^2}\le 0\)ならば(上に凸ということ)、\(\delta x\)の2次までの範囲では \(I[x+\delta x]\ge I[x]\)となる。\(\delta x\)が十分小さければ3次以上の項は 2次までの項に比して限りなく小さくなる(近似を用いているのはポテンシャルの項のみであることに注意。運動エネルギーの部分は近似をしていない。)。よって
軌道上で常に\(\frac{d^2 V}{d x^2}\le 0\)(上に凸)となる軌道は極小関数となる。
最小かどうかについては何も言えない。このように\(\delta x\)で展開する方法では何次まで展開しようと最小問題については何も結論をだせない。 自由粒子の場合は\(\frac{d^2 V}{d x^2}=0\)であり、自由落下の場合も\(\frac{d^2 V}{d x^2}=0\)なので極小の条件を 満たしていたのである。調和振動子の場合は\(\frac{d^2 V}{d x^2}=m\omega^2>0\)で、極小となるための十分条件を満たしていなかったのである。
与えられた軌道中で\(\frac{d^2V}{dx^2}>0\)となる部分があるとする。その軌道中での\(\frac{d^2V}{dx^2}\)の最大値を\(M\)としよう。そのとき \[ \frac{1}{2}m\int_{t_a}^{t_b}\delta \dot{x}^2\; dt -\frac{1}{2}\int_{t_a}^{t_b}\frac{d^2 V}{d x^2}\delta x^2\; dt \ge \frac{1}{2}m\int_{t_a}^{t_b}\delta \dot{x}^2\; dt -\frac{1}{2}M\int_{t_a}^{t_b}\delta x^2\; dt \] である。 だから任意の\(\delta x\)に対して \[ \frac{1}{2}m\int_{t_a}^{t_b}\delta \dot{x}^2\; dt -\frac{1}{2}M\int_{t_a}^{t_b}\delta x^2\; dt>0 \] なら、その軌道は極小関数だと言える。このことは、 調和振動子のときと全く同じように考えれば、 \[ \frac{\pi^2}{(t_b-t_a)^2}>\frac{M}{m} \] が成り立つこと同じことであることがわかる。これは\(t_b-t_a\)が十分小さければ成り立つ。だから
与えられた軌道があり、その軌道の十分微小な部分をとれば、それは極小関数になる。
と言える(図7-5)。
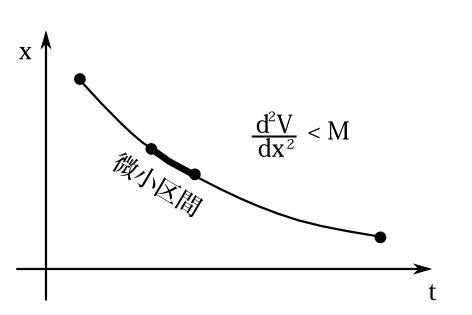
図7-5 与えられた軌道の微小区間を選べば、その軌道は極小関数となる。
7-8節 変分問題の最小性、極小性2
最後に一般のラグランジアンでの汎関数 \[ I[q]=\int_{t_a}^{t_b}L(q,\dot{q},t) \;dt \] の極小性について簡単に考察しよう。変換数を\(q+\delta q\)とすると \[ I[q+\delta q]=\int_{t_a}^{t_b}L(q+\delta q,\dot{q}+\delta \dot{q},t) \;dt \] であるが、これを\(\delta q\)と\(\delta \dot{q}\)の2次まで展開すると( \(\delta \dot{q}\)に関しては運動エネルギーの項にしか含まれないので元々2次までしかない)0次、1次、2次の項はそれぞれ
\begin{eqnarray} 0次:&\quad\quad& I[q]\notag\\ \notag\\ 1次:&\quad\quad& \int_{t_a}^{t_b}\sum_i\left[\frac{\partial\, L}{\partial\, q_i}-\frac{d}{dt}\left(\frac{\partial\, L}{\partial\, \dot{q_i}}\right)\right]\delta q_i\;dt\label{tui13}\\ \notag\\ 2次:&\quad\quad&\frac{1}{2} \int_{t_a}^{t_b}\sum_{i,j}\left[\frac{\partial\,^2 L}{\partial\, q_j\partial\, q_i}\delta q_i\delta q_j+ \frac{\partial\,^2 L}{\partial\, \dot{q}_j\partial\, \dot{q}_i}\delta \dot{q}_i\delta \dot{q}_j+\frac{\partial\,^2 L}{\partial\, \dot{q}_j\partial\, q_i}\delta q_i\delta \dot{q}_j+\frac{\partial\,^2 L}{\partial\, q_j\partial\, \dot{q}_i}\delta \dot{q}_i\delta q_j\right]\;dt\notag \end{eqnarray}
となる。ここで1次の項に関しては変分法のときの式(\ref{he3})の結果を使った。 \(q(t)\)を力学の法則を満たす軌道とすると、それはラグランジュ方程式を満たすので1次の項は0となる。今までわざわざ1次の項を計算して、そのつどそれが0となるとしていたが、この式を使えばわざわざ計算するまでもなかったのである。2次の項が任意の\(\delta q\)に対して常に正だと言えるなら、その軌道は極小関数だと言える。それはポテンシャル次第である。
直交座標では式(\ref{tui13})の2次の項は、\(q\)を\(x\)と書き換えて、 \begin{equation} -\frac{1}{2} \int_{t_a}^{t_b}\sum_{i,j}\frac{\partial\,^2 V}{\partial\, x_j\partial\, x_i}\delta x_i\delta x_j\;dt+\frac{1}{2} \int_{t_a}^{t_b} \sum_i m_i(\delta \dot{x}_i)^2\;dt \label{daini} \end{equation} となる。第2項は任意の\(\delta x\)に対して正となるので、第1項が任意の\(\delta x\)に対して0以上となる軌道は極小関数だといえる。 \(\frac{\partial\, V}{\partial\, x_j\partial\, x_i}\)は対称行列である。よく知られているように対称行列は直交行列で対角化できる。だからこの固有値が全て0以下ならば第1項は0以上となる。固有値がすべて0以下のときは、 幾何学的には1次元、2次元では、\(V\)が上に凸という意味である。3次元以上のときは図で表せないので幾何学的なイメージはないが、\(\frac{\partial\,^2 V}{\partial\, x_j\partial\, x_i}\)の固有値がすべて0以下のとき、それを上に凸であると呼ぶことにしよう。例えば \[ V=-x^2-2y^2-3z^2 \] は、固有値がすべて負なので上に凸である。今得られた結論は
定理7-5 極小関数となるための十分条件
ポテンシャル\(V\)が軌道上で常に上に凸なら、その軌道は極小関数である。
ということである。 極小かどうかは座標系によらないので、これは任意の座標系で成り立つことである。ポテンシャル\(V\)が軌道上で常には上に凸でない場合は、極小になるかどうかは式(\ref{daini})の第2項との兼ね合いであろう。この場合は、おそらく1次元の場合と同様、 積分時間が十分短ければ極小関数になる と思うのだが調べていない。
中心力ポテンシャルの場合
例として、中心力ポテンシャルの場合を考えよう。中心力ポテンシャルのラグランジアンは2次元極座標表示で \[ L=\frac{1}{2}m(\dot{r}^2+r^2\dot{\theta}^2)-V(r) \] である。このラグランジアンで、2階微分はそれぞれ \begin{eqnarray} &&\frac{\partial\,^2 L}{\partial\, \dot{r}^2}=m,\quad \quad \frac{\partial\,^2 L}{\partial\, \dot{\theta}^2}=mr^2,\quad\quad \frac{\partial\,^2 L}{\partial\, r^2}=m\dot{\theta}^2-\frac{\partial\,^2 V}{\partial\, r^2},\notag\\ &&\frac{\partial\,^2 L}{\partial\, r\partial\, \dot{\theta}}=2mr\dot{\theta},\quad \frac{\partial\,^2 L}{\partial\, \dot{\theta}\partial\, r}=2mr\dot{\theta}\notag \end{eqnarray} なので、式(\ref{tui13})の2次の項は
\begin{equation} \frac{1}{2} \int_{t_a}^{t_b} \left[ m(\delta\dot{r})^2+mr^2(\delta\dot{\theta})^2+m\dot{\theta}^2(\delta r)^2-\frac{\partial\,^2 V}{\partial\, r^2}(\delta r)^2+4mr\dot{\theta}(\delta r)(\delta\dot{\theta}) \right]dt \label{h192} \end{equation}
となる。これでは見通しがわるいので\(mr^2(\delta\dot{\theta})^2+4mr\dot{\theta}(\delta r)(\delta\dot{\theta})\) を\(\delta \dot{\theta}\)の完全平方にすると、これは \[ mr^2\left( (\delta \dot{\theta})^2+\frac{4\dot{\theta}(\delta r)(\delta\dot{\theta})}{r} \right) = mr^2\left[ (\delta \dot{\theta})+\frac{2}{r}\dot{\theta}(\delta r) \right]^2 - 4m\dot{\theta}^2(\delta r)^2 \] となる。 これを式(\ref{h192})に代入すると \begin{equation} \frac{1}{2} \int_{t_a}^{t_b} \left[ m(\delta\dot{r})^2 + mr^2\left[ (\delta \dot{\theta})+\frac{2}{r}\dot{\theta}(\delta r) \right]^2 + \left( -3m\dot{\theta}^2-\frac{\partial\,^2 V}{\partial\, r^2} \right) (\delta r)^2 \right]dt \label{h193} \end{equation} となる。これが任意の\(\delta r,\delta \theta\)で正なら、力学の法則を満たす軌道は極小になるわけである。この第1項と第2項は必ず正になる。もし第3項が常に正となるような軌道なら、その軌道は極小となる。正でないときは、第1項、第2項とのかねあい次第で極小にならない場合もあろう。
中心力ポテンシャルの場合角運動量である\(mr^2\dot{\theta}\)は一定なので、\(mr^2\dot{\theta}=h\)とおくと、 \(3m\dot{\theta}^2\)は \[ 3m\frac{h^2}{m^2r^4}=3\frac{h^2}{mr^4} =\frac{\partial\,^2}{\partial\, r^2}\left(\frac{h^2}{2mr^2}\right) \] となる。だから 式(\ref{h193})は \[ \frac{1}{2} \int_{t_a}^{t_b} \left[ m(\delta\dot{r})^2 + mr^2\left[ (\delta \dot{\theta})+\frac{2h^2}{r^3}(\delta r) \right]^2 -\frac{\partial\,^2}{\partial\, r^2} \left( \frac{h^2}{2mr^2}+V(r) \right) (\delta r)^2 \right]dt \] と書きかえられる。中心力の場合 \begin{equation} m\ddot{r}=-\frac{\partial\,}{\partial\, r} \left( \frac{h^2}{2mr^2}+V(r) \right) \label{iu} \end{equation} が成り立つので (注 \(r\)成分のラグランジュ方程式は(2章の式(25)参照) \[ m\ddot{r}=mr\dot{\theta}^2-\frac{\partial\, V}{\partial\, r} \] である。\(h=mr^2\dot{\theta}\)を使うと、 \[ mr\dot{\theta}^2=mr\frac{h^2}{m^2h^4}=\frac{h^2}{mr^3}=-\frac{\partial\,}{\partial\, r} \left(\frac{h^2}{2mr^2}\right) \] となる。だから式(\ref{iu})になるのである。 ) \( \frac{h^2}{2mr^2}+V(r) \) は\(r\)方向の有効ポテンシャルと言える。\(\frac{h^2}{2mr^2}\)は遠心力のポテンシャルである。そこで \[ V_e(r)\equiv\frac{h^2}{2mr^2}+V(r) \] とおこう。軌道が\(\frac{d^2V_e}{dr^2}<0\)となる所のみを通るなら、その軌道は極小関数になるわけである。
万有引力のとき
今、ポテンシャルとして万有引力形の \[ V=-\frac{k}{r} \] としよう。。ここで\(k\)は定数。この場合の\(V\)は上に凸ではないので、あらゆる軌道が極小関数になるとは断定できない(定理7-5参)。\(V_e(r)\)は 図7-6のようになる。
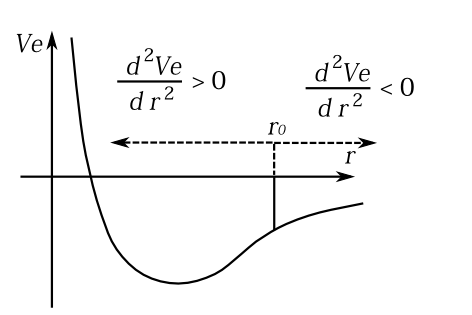
図7-6 軌道が有効ポテンシャルの上に凸な部分のみを通るときは極小関数となる。
\(\frac{d^2 V_e}{d r^2}\)は\(r\)の小さいところでは正である。ある大きさ\(r_0\)以上のところでは負になる。だから\(r>r_0\)となるところのみ通る軌道は極小関数になる。又\(h=0\)のときは、これは運動が\(r\)方向の場合だが、有効ポテンシャル\(V_e\)は万有引力形のポテンシャルになり\(\frac{d^2}{dr^2}\left(-\frac{k}{r}\right)\)は常に負なので(図7-7)、そういう軌道は極小関数になる。
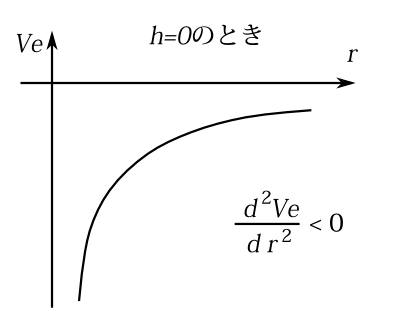
図7-7 軌道の角運動量が0のときは有効ポテンシャルは全領域で上に凸になるので極小関数になる。
以上少し長くなってしまったが、力学の法則を満たす軌道\(q(t)\)が汎関数 \[ I[q]=\int_{t_a}^{t_b}L(q,\dot{q},t)\; dt \] の停留関数になることを最小作用の原理と呼ぶ文献もあるが、決して最小になるわけではないとうことがわかったと思う。そして最小とならないのは、決して特殊な状況でなはく、通常の軌道で最小にならないのである。
7-9節 まとめ
汎関数 \[ I[x]=\int^{t_b}_{t_a}f(x,\dot{x},t)dt \] で、\(x(t)\)が停留関数であるための必要十分条件は、\(x(t)\)がオイラーの方程式 \[ \frac{d}{dt}\left(\frac{\partial\, f}{\partial\, \dot{x}_i}\right)=\frac{\partial\, f}{\partial\, x_i} \] を満たすことである。力学の法則を見たす軌道\(q_i\)はラグランジアン\(L\)に対してオイラーの方程式 \[ \frac{d}{dt}\left(\frac{\partial\, L}{\partial\, \dot{q}_i}\right)=\frac{\partial\, L}{\partial\, q_i} \] を満たす。ということは力学の法則を満たす軌道は汎関数 \[ I[q]=\int^{t_b}_{t_a}L(q,\dot{q},t)dt \] の停留関数である。これとは別に力学の法則を満たす軌道は \[ I[q,p]=\int^{t_b}_{t_a}\sum_ip_i\dot{q}-H(q,p,t)dt \] の停留関数でもある。 力学の法則を満たす軌道がこの汎関数の極小関数になるかどうかはポテンシャル、空間上どこを通るか、積分範囲である時間、による。軌道が、ポテンシャルが上に凸の部分のみを通るなら、その軌道は極小関数になる。また、時間が十分に短い軌道は極小関数になると思う。