第5章 正準変換
この章は飛ばしてもらっても後の章の理解に一切関係ない。正準変換というのは微分方程式の変数変換なのだが、実際問題に役に立つわけではない。役に立つ場合もあるのかもしれないが私は知らない。後の章との関係では単にハミルトンヤコビの方程式の導出に使っているだけである。しかしながらハミルトンヤコビの方程式の解から正準方程式の解が得られることの証明は次の章で簡潔に記してある。ここでの導出は単に歴史的な興味しか無いと思う。 例題を多く入れたが、計算自体は簡単なものなので、概念がわかりづらいときは飛ばさずにした方がいいと思う。概要としてはまず正準変換の定義をした。しかしこの定義は世間一般の定義とは異なるようなので注意してほしい。このテキストで正準変換に含まれる変換で、世間一般での正準変換に含まれないものもある(付録B参照)。それから正準変換というものの性質について説明した。正準変換というものは解軌道を対応させるものなのである。その後、母関数による正準変換の説明をした。これが世間でいう正準変換というもののようである。これは巧妙ゆえにわかりづらいものである。他の本にあるような変分法に基礎を置かず微分に基礎をおいた説明をしている。変分法の(最小ならまだわかりやすいのだが)停留というのはわかりづらいし数学的に厳密性にかけているような気がするからである。
5-1節 正準変換の定義
正準変換というのは、大ざっぱに言えば、正準変数\(q,p\)を変数変換して、新たな変数でも正準方程式を満たす変換のことである。以下で正準変換の明確な定義を与えるが言葉の意味というのは文脈によって異なるものなので、柔軟にとらえてもらいたい。また、世間一般の正準変換より広い意味で定義している。尚、この章での\(H,K\)はハミルトニアンの定義である \( \sum_i p_i\dot{q}_i -L \) である必要は全くない。
正準変換の定義
1. \(q,p,H(q,p,t)\)は正準方程式
\begin{equation}
\frac{\partial\, H}{\partial\, p_i}=\dot{q}_i\qquad\qquad \frac{\partial\, H}{\partial\, q_i}=-\dot{p}_i
\label{s1}
\end{equation}
を満たす。
2. \(q,p\to Q,P\)という変換があり、それは
逆変換可能である、
3. 1を満たすなら、\(Q,P,t\)の関数\(K(Q,P,t)\)と\(q,p\)から変換された\(Q,P\)は正準方程式
\[
\frac{\partial\, K}{\partial\, P_i}=\dot{Q}_i\qquad\qquad \frac{\partial\, K}{\partial\, Q_i}=-\dot{P}_i
\]
を満たす。
このとき\(q,p,H\to Q,P,K\)の変換を正準変換と呼ぶことにしよう。
例えば直交座標を極座標に変換し、\(H=K\)とするのも正準変換である。この場合は位置座標同士の変換であり、\(H=K\)であるが、正準変換は位置座標同士の変換である必要はないし、\(H=K\)である必要もない。
例5-1
\[ Q=p\qquad\qquad P=-q\qquad\qquad K=H \] は正準変換である。実際 \[ \frac{\partial\, K}{\partial\, P}=\frac{\partial\, H}{\partial\,(-q)}=\dot{p}=\dot{Q} \] すなわち正準方程式 \[ \frac{\partial\, K}{\partial\, P}=\dot{Q} \] が成り立っている。又 \[ \frac{\partial\, K}{\partial\, Q}=\frac{\partial\, H}{\partial\, p}=\dot{q}=-\dot{P} \] すなわち正準方程式 \[ \frac{\partial\, K}{\partial\, Q}=-\dot{P} \] が成り立っている。【例終】
5-2節 正準変換についての幾つかの性質
この節では、記述の簡潔性と図での扱いのため、正準変数を\(q\)を1つ、\(p\)を1つとするが、それで本質的なことは何ら変わることはない。この節での主張は\(q,p\)が何個あっても通じる内容である。
任意の座標変換に対する正準変換
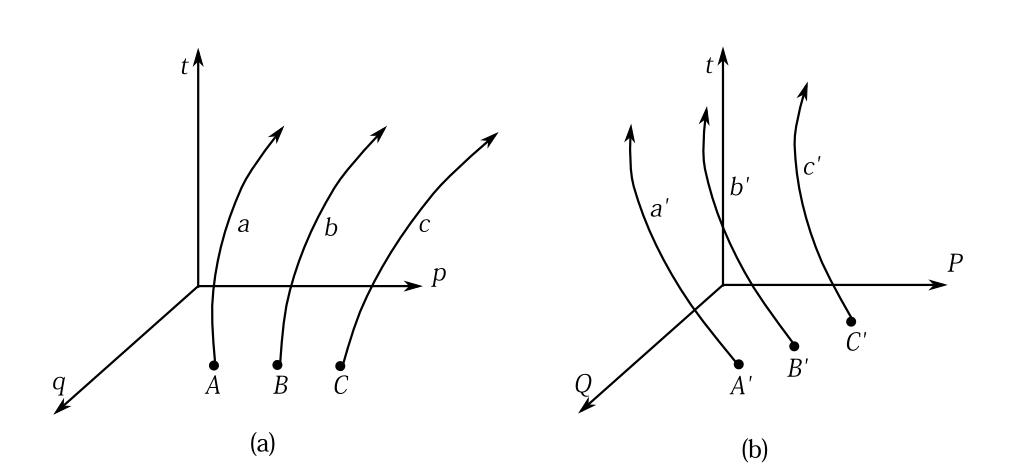
図5-1 座標変換による軌道の変化。(a): \(\dot{q}=\frac{\partial\, H(q,p,t)}{\partial\, p}, \quad \dot{p}=-\frac{\partial\, H(q,p,t)}{\partial\, q}\) なので\(q,p,t\)を決めれば\(\dot{q},\dot{p}\)は決まる。 (b):a,b,c軌道を\(Q,P\)座標へ変換したものがa',b',c'軌道。座標\(Q,P\)が決まれば\(\dot{Q},\dot{P}\)も決まる。
正準変換というものを図形的に考えてみよう。 \(\dot{q},\dot{p}\)は正準方程式(\ref{s1})によって決まり、\(\partial\, H/\partial\, p,\partial\, H/\partial\, q\)は\(q,p,t\)の関数だから、\(\dot{q},\dot{p}\)は\(q,p,t\)で決まる。だから\(q,p,t\)空間では図5-1(a)のように解軌道の流れ場があるのである。 \(q,p\to QP\)へ変換すると、この解軌道群は\(QP,t\)空間上での軌道群に変換される(5-1(b))。だから変換\(q,p\to Q,P\)が与えられれば\(\dot{Q},\dot{P}\)は\(Q,P,t\)の関数として定まる 。その関数を \(\dot{Q}(Q,P,t),\dot{P}(Q,P,t)\)と書こう (注 \(\dot{Q},\dot{P}\)は \begin{eqnarray} \dot{Q}&=&\frac{\partial\, Q}{\partial\, q}\dot{q}+\frac{\partial\, Q}{\partial\, p}\dot{p}+\frac{\partial\, Q}{\partial\, t}\notag\\ &=&\frac{\partial\, Q}{\partial\, q}\frac{\partial\, H}{\partial\, p}-\frac{\partial\, Q}{\partial\, p}\frac{\partial\, H}{\partial\, q}+\frac{\partial\, Q}{\partial\, t}\notag \end{eqnarray} である。同様に \begin{eqnarray} \dot{P}&=&\frac{\partial\, P}{\partial\, q}\dot{q}+\frac{\partial\, P}{\partial\, p}\dot{p}+\frac{\partial\, P}{\partial\, t}\notag\\ &=&\frac{\partial\, P}{\partial\, q}\frac{\partial\, H}{\partial\, p}-\frac{\partial\, P}{\partial\, p}\frac{\partial\, H}{\partial\, q}+\frac{\partial\, P}{\partial\, t}\notag \end{eqnarray} である。この右辺を\(Q,P,t\)で表したものが関数\(\dot{Q}(Q,P,t),\dot{P}(Q,P,t)\)となる。 )。 この変換が正準変換の条件を満たすためには、\(K\)は \[ \frac{\partial\, K}{\partial\, P}=\dot{Q}(Q,P,t)\qquad\qquad \frac{\partial\, K}{\partial\, Q}=-\dot{P}(Q,P,t) \] を満たさなければならない。そのような\(K\)が存在するための必要十分条件は、よく知られているように、 \begin{equation} -\frac{\partial\, \dot{P}(Q,P,t)}{\partial\, P}=\frac{\partial\, \dot{Q}(Q,P,t)}{\partial\, Q} \label{dde1} \end{equation} を満たすことである (注 これは正準変数が\(q,p\)が1つづつの場合である。2つ以上のときは、もう少し必要な式が増える。 ) 。 しかしながら、任意の変換\(q,p\to Q,P\)が必ずしもこの式を満たすわけではない。 だから
定理5-1 任意の座標・運動量変換\(q,p\to Q,P\)に対して、正準方程式を満たす\(K\)が必ず存在するわけではない。
と言える。
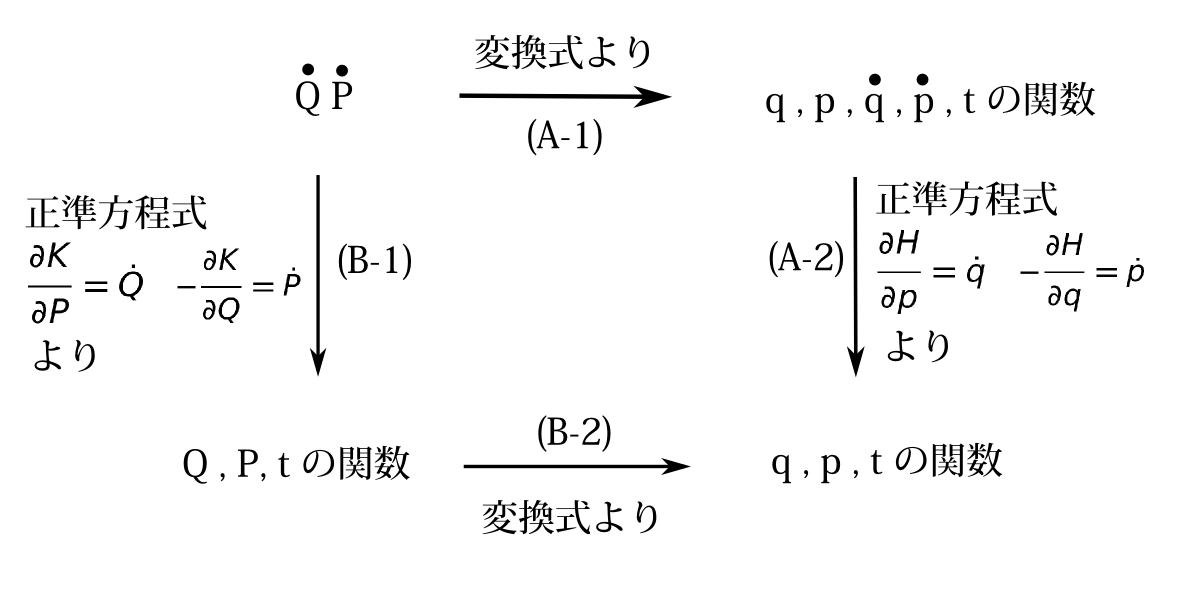
図5-2 正準変換であるかを調べるための手順
今のことを図5-2を使って図式的に説明しよう。\(\dot{Q},\dot{P}\)は変換式より\(q,p,\dot{q},\dot{p},t\)の関数として表せる(A-1)。\(\dot{q},\dot{p}\)は正準方程式より\(q,p,t\)の関数として表せるので\(\dot{Q},\dot{P}\)は\(q,p,t\)の関数として表せる(A-2)。そして変換式より\(q,p\)は\(Q,P,t\)で表されるので\(\dot{Q},\dot{P}\)は\(Q,P,t\)の関数として表せる(B-2の逆)。その表した式がそれぞれ\(\frac{\partial\, K}{\partial\, P},-\frac{\partial\, K}{\partial\, Q}\)になっていなければ正準変換にはならないのである(B-1)。そうなる\(K\)は必ずしも存在するわけではない。 今の説明からわかると思うが、与えられた変換\(q,p,H\to Q,P,K\)が正準変換かどうかは\(\dot{Q},\dot{P}\)を(A-1)(A-2)の手順で\(q,p,t\)で表したものと(B-1)(B-2)の手順で\(q,p,t\)で表したものが一致しているかどうかで判定できる。一致していればそれは正準変換であり、一致していなければ正準変換ではない。
例題5-1 \[ H=\frac{p^2}{2} \] として \begin{equation} Q=q+p,\quad P=p \label{da0} \end{equation} という変換で、正準方程式を満たす\(K\)は存在するか。もし存在するなら求めよ。
【解】変換を逆に解くと \begin{equation} q=Q-P\qquad\qquad p=P \label{da1} \end{equation} である。又、変換式(\ref{da0})より \begin{equation} \dot{Q}=\dot{q}+\dot{p},\quad \dot{P}=\dot{p} \label{da3} \end{equation} である(図5-2、A-1)。正準方程式から \[ p=\dot{q} \qquad\qquad 0=\dot{p} \] である。これを式(\ref{da3})に入れると \[ \dot{Q}=p\qquad\qquad \dot{P}=0 \] となる(図5-2、A-2)。式(\ref{da1})を使うと \begin{equation} \dot{Q}=P \qquad \dot{P}=0 \label{da4} \end{equation} である(図5-2、B-2の逆)。 これで\(\dot{Q},\dot{P}\)が\(Q,P,t\)の関数で表せた。\(K\)が存在するための条件式(\ref{dde1})は \[ -\frac{\partial\, \dot{P}}{\partial\, P}=0 \qquad\qquad\frac{\partial\, \dot{Q}}{\partial\, Q}=0 \] となって満たされる。よって正準方程式を満たす\(K\)が存在する。\(K\)は正準方程式を満たすように決めればよい。式(\ref{da4})を使うと \[ \frac{\partial\, K}{\partial\, P}=P \qquad\qquad \frac{\partial\, K}{\partial\, Q}=0 \] を満たしていれば良いわけである。だから \[ K=\frac{P^2}{2} \] とすればよい。 これが正準方程式を満たす\(K\)である。【解答終】
\(K\)に対応する正準変換
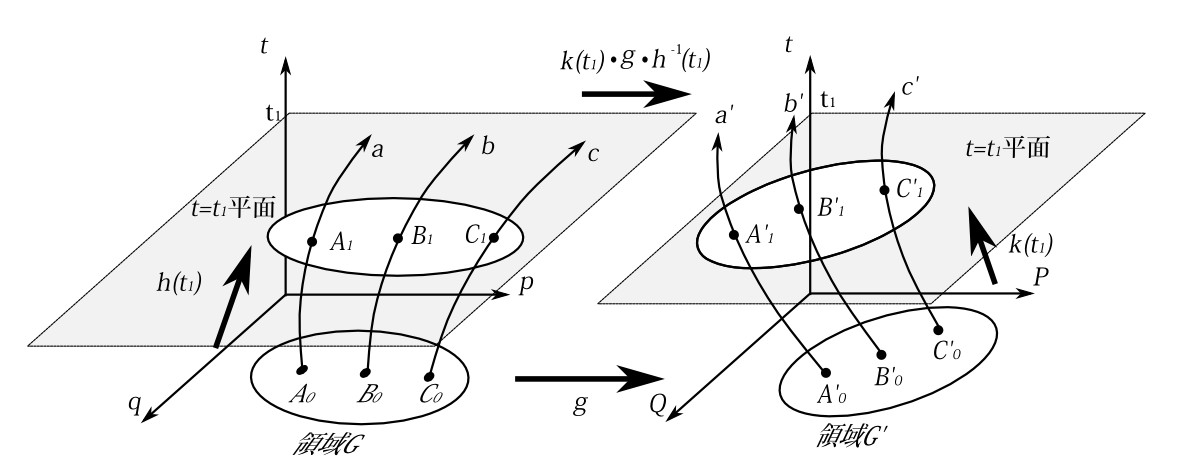
図5-3 \(t=0\)での変換\(q,p\to Q,P\)を任意に決める。解軌道を対応させれば変換は決まる。
一方、
定理5-2 与えられた\(K\)に対応する正準変換は必ず存在する。
【証明】 \(q,p,t\)空間で\(t=0\)のある領域\(G\)を、連続という条件を満たして、\(G'\)に変換する(図5-3)。これでまず\(t=0\)での\(q,p\)から\(Q,P\)への変換を決めたわけである。領域\(G\)のある点\(A_0\)を初期条件とすると\(q,p,t\)空間では軌道\(a\)が決まる。\(A_0\)に対応する\(Q,P,t\)空間での点を\(A'_0\)としよう。\(K\)は与えられているので、これによって軌道の時間発展は完全に決まる。その軌道を\(a'\)としよう。\(t=0\)以外の時間での変換だが、\(t=t_1\)で 軌道\(a\)が\(A_1\)、軌道\(a'\)が\(A'_1\)にあるなら、\(t=t_1\)では\(A_1\to A'_1\)と変換させればよい。このようにして 初期条件を変えれば他の軌道ができ、同様にその軌道と、それに対応する軌道ができ、\(t=t_1\)での変換がきまる。同じ論法であらゆる時刻での変換が決まる。すなわち、ある時刻、今の場合\(t=0\)、での\(q,p\)から\(Q,P\)への変換を決めてやれば、他の時刻での変換は一意的に決まる。そしてこの\(Q,P\)の軌道は \[ \frac{\partial\, K}{\partial\, P}=\dot{Q}\qquad\qquad \frac{\partial\, K}{\partial\, Q}=-\dot{P} \] を満たすように決めたのだから、その新しい変数\(Q,P\)は与えられた\(K\)に対して正準方程式を満たす。【証明終】
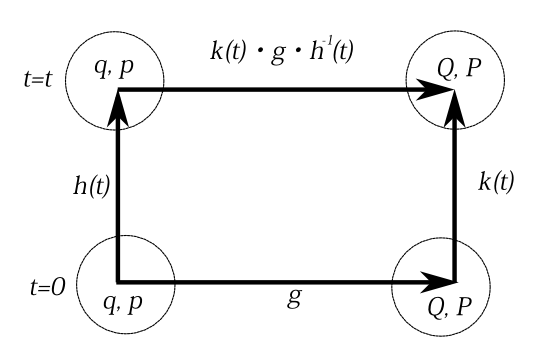
図5-4 変換の模式図。任意の時間\(t\)での変換\(q,p\to Q,P\)は、一端, 解軌道上を\(t=0\)の点まで戻す、\(t=0\)での任意の変換\(g\)で\(QP\)上の点に移し、そこから解軌道にそって時間\(t\)での点に移せば良い。
さて今のことを 記号を使って簡潔に書こう。\(q,p\)空間上の\(t=0\)の点は解軌道にそって動き、\(t=t_1\)のときは\(q,p\)空間上のある点に移る。この\(q,p\to q,p\)への写像を\(h(t_1)\)と書こう(図5-3、図5-4)。同様に\(Q,P\)空間上の\(t=0\)の点が\(t=t_1\)のときに移る写像を\(k(t_1)\)と書こう。\(t=0\)での\(q,p\to QP\)の写像を\(g\)と書こう。すると\(t=t_1\)での\(q,p\to Q,P\)の写像は \begin{equation} k(t_1)\cdot g\cdot h^{-1}(t_1) \label{ir1} \end{equation} となるわけである。
さて、今証明したように\(q,p,H\to Q,P,K\)の変換が正準変換だというのは\(q,p,t\)空間の解軌道と\(Q,P,t\)空間の解軌道が対応しているということであった。となると、この逆の \(Q,P,K\to q,p,H\)という変換も解軌道が対応しているので、正準変換になる。すなわち
定理5-3 正準変換の逆変換も正準変換になる。
そして\(q,p,H\to Q,P,K\)が正準変換で、さらに\(Q,P,K\to Q',P',K'\)が正準変換なら、これを続けて行った、 \(q,p,H\to Q',P',K'\)も正準変換になる。このことと、今述べた定理5-3から、
定理5-4 正準変換は群をなす
と言える。ただ、群をなすからといってこの性質をあとで使うわけではない。
例題5-2 \[ H=\frac{p^2}{2m}-mgq\qquad K=Q \] のときの正準変換を求めよ。\(H\)は自由落下でのハミルトニアンである。
【解】\(q,p\)についての正準方程式は \[ \frac{p}{m}=\dot{q}\qquad mg=\dot{p} \] となり、これから \[ q=\frac{1}{2}\,g\,t^2+\frac{p_0}{m}\,t+q_0 \qquad\qquad p=mgt+p_0 \] と求まる。ここで\(q_0,p_0\)は\(t=0\)での\(q,p\)の値。一方\(Q,P\)の正準方程式は \[ 0=\dot{Q}\qquad\qquad -1=\dot{P} \] であり、これから \[ Q=Q_0 \qquad\qquad P=-t+P_0 \] と求まる。ここで\(Q_0,P_0\)は\(t=0\)での\(q,p\)の値。 式(\ref{ir1})での\(h^{-1}(t)\)は \[ h^{-1}(t):\quad q_0=q-\frac{1}{2}gt^2-\frac{p-mgt}{m}\,t\qquad p_0=p-mgt \] となる。\(k(t)\)は \[ k(t):\quad Q=Q_0 \qquad\qquad P=P_0-t \] となる。\(g\)として恒等変換を選ぶ、すなわち\(g\)を \[ g:\quad Q_0=q_0\qquad\qquad\qquad P_0=p_0 \] とすると \(k(t)\cdot g\cdot h^{-1}(t)\)は \[ Q=q-\frac{1}{2}\,g\,t^2-\frac{p-mgt}{m}\,t \qquad\qquad P=p-mgt-t \] となる。
念のためにこの変換が正準変換となっていることを図5-2の方法で直接確かめてみよう。まず変換式より(A-1) \[ \dot{Q}=\dot{q}-gt-\frac{\dot{p}-mg}{m}t-\frac{p-mgt}{m} \qquad\qquad \dot{P}=\dot{p}-mg-1 \] となる。そして正準方程式\(\frac{p}{m}=\dot{q},mg=\dot{p}\)を使って\(\dot{q},\dot{p}\)を消すと(A-2) \[ \dot{Q}=\frac{p}{m}-gt-\frac{mg-mg}{m}t-\frac{mg-mgt}{m}=0 \qquad\qquad \dot{P}=mg-mg-1=-1 \] となる。一方\(Q,P\)系の正準方程式を使うと(B-1) \[ \dot{Q}=0\qquad\dot{P}=-1 \] となり、この2つの方法で求めた\(\dot{Q},\dot{P}\)は一致する。よって正準変換であることが確かめられた。 【解答終】
5-3節 母関数による正準変換1
さて、これから母関数による正準変換について説明する。 それは巧妙で、わかりづらい理屈である。まず準備として次の命題を述べよう。
定理5-5 \(q,p\)が、\(q,p,t\)の関数(ではあるが\(\dot{q},\dot{p}\)の関数ではない)\(H(q,p,t)\)に対して、正準方程式を満たすことと、\(q,p\)が \[ \mathcal{L}\equiv\sum_i p_i\dot{q}_i-H(q,p,t) \] についてのオイラーの方程式を満たすことは同値である。
【証明】
\(\mathcal{L}\)に対して\(p_i,q_i\)についてのオイラーの方程式は、\(p_i\)については
\[
0=\dot{q}_i-\frac{\partial\, H}{\partial\, p_i}
\]
\(q_i\)については
\[
\dot{p}_i=-\frac{\partial\, H}{\partial\, q_i}
\]
となり、正準方程式と一致する。【証明終】
だから、
1. \(P,Q\)が\(K(Q,P,t)\)に対して正準方程式を満たすためには
\[
\mathcal{L'}\equiv\sum_i P_i\dot{Q}_i-K(Q,P,t)
\]
が\(P,Q\)についてのオイラーの方程式を満たしていればよい。
さて定理1-1の等式4で述べたように\(q,p,t\)の任意の関数\(F\)の時間微分\(dF(q,p,t)/dt\)は\(q,p\)について、オイラーの方程式を満たす
(注 等式4での
\(f\)が\(F\)、\(q\)が\(q,p\)に対応)
。\(q,p\)が\(H\)に対して正準方程式を満たしているのだから
\[
\mathcal{L}+\frac{d F(q,p,t)}{dt}
\]
は\(q,p\)についてのオイラーの方程式を満たしている。
定理1-3で述べたように、ある変数に対してオイラーの方程式が成り立つなら、逆変換可能な変数変換\(q,p\to Q,P\)
で
(注
逆変換可能なことが必要なのは定理1-2で述べたように\(q,p\)が\(Q,P\)で表されることが必要だから。
)
、その新たな変数\(Q,P\)についてもオイラーの方程式が成り立つのであった。だから
2. \(\mathcal{L}+d F(q,p,t)/dt\)は\(Q,P\)についてもオイラーの方程式を満たしている
(注
もちろん、これを\(Q,P,\dot{Q},\dot{P},t\)の関数であらわしたときにオイラーの方程式を満たしているという意味である。)
。
\(\mathcal{L}+d F(q,p,t)/dt\)は
\[
\mathcal{L}+\frac{dF(q,p,t)}{dt}=
\sum_i p_i\dot{q}_i-H+\sum_i \frac{\partial\, F}{\partial\, q_i}\dot{q}_i+\sum_i \frac{\partial\, F}{\partial\, p_i}\dot{p}_i+\frac{\partial\, F}{\partial\, t}
\]
であり、\(q,p,\dot{q},\dot{p},t\)の関数である。そして定理1-8より\(Q,P,\dot{Q},\dot{P},t\)の関数である。それでもし
3.
変換\(q,p\to Q,P\)を使って、\(\mathcal{L}+d F(q,p,t)/dt\)を\(Q,P,\dot{Q},\dot{P},t\)の関数で表したとき、これが\(\mathcal{L}'\)となる
なら、1と2より\(Q,P,K\)は正準方程式を満たす。
まとめると
定理5-6
1. \(q,p,H\)が正準方程式を満たす。
2. 変換\(q,p\to Q,P\)は逆変換可能である。
3. この変換\(q,p\to Q,P\)を使うと
\begin{equation}
\sum_i P_i\dot{Q}_i-K=\sum_i p_i\dot{q}_i-H+\frac{d F(q,p,t)}{dt}
\label{s62}
\end{equation}
は\(Q,P,\dot{Q},\dot{P},t\)についての恒等式となる
。
このとき\(Q,P\)は\(K\)に対して正準方程式を満たす。すなわち\(q,p,H\to Q,P,K\)は正準変換となる。
式(\ref{s62})が成り立つことの意味は、\(Q,P,\dot{Q},\dot{P},t\)についての恒等式になることであり、定理1-9より\(q,p,\dot{q},\dot{p},t\)についての恒等式になることである。しかし、決して正準方程式を使って \(\dot{q},\dot{p}\)を\(q,p,t\)で表し、その結果\(q,p,t\)の(同じことだが\(Q,P,t\)の)恒等式になるという意味ではない(例題5-4参照)。 尚、\(F\)は母関数という (注 母関数\(F\)の定義が通常の文献とは符号が逆になっていることに注意。 ) 。 式(\ref{s62})を満たす正準変換が世間一般での正準変換の定義である。正準変換ではあるが式(\ref{s62})を満たさないものもある。すなわち
定理5-7
\[
\sum_i P_i\dot{Q}_i-K=\sum_i p_i\dot{q}_i-H+\frac{d F(q,p,t)}{dt}
\]
を満たすことは正準変換のための必要条件ではない。
その例は本筋と関係ないことなので付録Bに記した (注 2022年10月追記:正準変換のための必要十分条件は \[ \sum_i P_i\dot{Q}_i-K=\sum_i p_i\dot{q}_i-H+G(q,\dot{q},p,\dot{p},t) \] で、\(G\)がオイラーの方程式を満たすことである。\(G\)が\(dF/dt\)なら、もちろんオイラーの方程式を満たすが、必ずしも時間の全微分である必要はない(付録B参照)。) 。
例題5-3 \begin{equation} Q=-p-qt \qquad\qquad P=q \label{qq1} \end{equation} \[ H=q\qquad\qquad K=P-\frac{P^2}{2} \] という変換は正準変換になる。そのことを 式(\ref{s62})が \[ F=-qp-\frac{1}{2}q^2t \] とすれば成り立つことを示し、確認せよ。
【解】 式(\ref{qq1})を逆に解くと \[ q=P \qquad\qquad p=-Q-Pt \] となるので、この変換は逆変換可能であり、定理5-6の2が満たされる。これを使って\(F\)を\(Q,P,t\)で表すと \begin{eqnarray} F&=&-P(-Q-Pt)-\frac{1}{2}P^2t\notag\\ &=&PQ+\frac{1}{2}P^2t\notag \end{eqnarray} となる。\(\mathcal{L}+d F(q,p,t)/dt\)を\(Q,P,\dot{Q},\dot{P},t\)で表すと \begin{eqnarray} p\dot{q}-H+\frac{dF}{dt}&=& (-Q-Pt)\dot{P}-P+\left( \dot{P}Q+P\dot{Q}+Pt\dot{P}+\frac{P^2}{2} \right)\notag\\ &=&P\dot{Q}-\left(P-\frac{P^2}{2}\right)\notag \end{eqnarray} となる。これは \( \mathcal{L}' \) になっている。だからこの変換は正準変換になっている。
念のためにこの変換が正準変換となっていることを図5-2の方法で直接確かめてみよう。まず変換式より(A-1) \[ \dot{Q}=-\dot{p}-\dot{q}t-q \qquad\qquad \dot{P}=\dot{q} \] となる。そして正準方程式より\(0=\dot{q},-1=\dot{p}\)である。これを使って\(\dot{q},\dot{p}\)を消すと(A-2) \[ \dot{Q}=1-q \qquad\qquad \dot{P}=0 \] となる。一方\(Q,P\)系の正準方程式を使うと(B-1) \[ \dot{Q}=1-P \qquad\dot{P}=0 \] となる。そして変換式より(B-2) \[ \dot{Q}=1-q \qquad\qquad \dot{P}=0 \] となり、この2つの方法で求めた\(\dot{Q},\dot{P}\)は一致する。よって正準変換であることが確かめられた。 【解答終】
例題5-4 変換式\(q,p\to Q,P\)が恒等変換、すなわち \begin{equation} Q=q\qquad\qquad P=p \label{tok1} \end{equation} で、\(H,K\)がそれぞれ \[ H=\frac{p^2}{2}-\frac{q^2}{2} \qquad\qquad K=-\frac{P^2}{2}-\frac{3}{2}Q^2 \] のときは正準変換ではない。そして \[ F=pq \] のときは 式(\ref{s62})も満たされない。しかし、正準方程式の結果を使って、式(\ref{s62})を\(q,p,t\)又は\(Q,P,t\)で表せば、式(\ref{s62})は満たされてしまう。以上のことを示せ。
【解】まず正準変換ではないことを示そう。
図5-2の手順に沿って示すことにする。
(A-1)変換式から
\[
\dot{Q}=\dot{q}\qquad\qquad\dot{P}=\dot{p}
\]
(A-2)正準方程式から\(\dot{q}=p,\dot{p}=q\)なので
\[
\dot{Q}=p\qquad\qquad \dot{P}=q
\]
となる。もう一つの方法で\(\dot{Q},\dot{P}\)を計算する。
(B-1)正準方程式から
\[
\dot{Q}=-P\qquad\qquad\dot{P}=3Q
\]
(B-2)変換式から
\[
\dot{Q}=-p\quad\quad \dot{P}=3q
\]
2つの方法で得られた\(\dot{Q},\dot{P}\)が一致しないのでこれは正準変換ではない。
次に \begin{equation} \mathcal{L'}=\mathcal{L}+\frac{dF}{dt} \label{tok4} \end{equation} が\(q,p,\dot{q},\dot{p},t\)の恒等式になっていないことを示そう。 \(\mathcal{L'}\)を\(q,p,\dot{q},\dot{p},t\)で表すと \begin{equation} \mathcal{L'}=P\dot{Q}-\left(-\frac{P^2}{2}-\frac{3}{2}Q^2\right)=p\dot{q}+\frac{p^2}{2}+\frac{3}{2}q^2 \label{tok2} \end{equation} となる。一方、\(\mathcal{L}+\frac{dF}{dt}\)を\(q,p,\dot{q},\dot{p},t\)で表すと \begin{equation} \mathcal{L}+\frac{dF}{dt}=p\dot{q}-\left(\frac{p^2}{2}-\frac{q^2}{2}\right)+(p\dot{q}+q\dot{p})= 2p\dot{q}+q\dot{p}-\frac{p^2}{2}+\frac{q^2}{2} \label{tok3} \end{equation} である。式(\ref{tok2})、(\ref{tok3})より、式(\ref{tok4})は\(q,p,\dot{q},\dot{p},t\)の恒等式になっていない。
ところが正準方程式から得られる \[ \dot{q}=p\qquad \qquad \dot{p}=q \] を使うと \[ \mathcal{L'}=\frac{3}{2}{p^2}+\frac{3}{2}q^2 \] となり、 \[ \mathcal{L}+\frac{dF}{dt}=\frac{3}{2}{p^2}+\frac{3}{2}q^2 \] となり、式(\ref{tok4})は\(q,p,t\)についての恒等式となる。【解答終】
5-4節 母関数による正準変換2
さて、正準変換になるためには式(\ref{s62})を満たせばよいということはわかったが、このままでは使いづらいので、式(\ref{s62})をもっと具体的な形にしてみよう。 そこでやや天下り的だが、
変換\(q,p\to Q,P\)は逆変換可能なことは当然として、そのうえ\(q,p\)が\(q,Q\)で表せるような変換に限定する
としよう 。 例えば \[ Q=q+p\qquad\qquad P=q-p \] という変換なら \[ q=q \qquad\qquad p=Q-q \] というように\(q,p\)は\(q,Q\)で表せる。しかし \[ Q=2q\qquad\qquad P=q-p \] は\(q,Q\)で\(p\)を表すことが出来ない。 尚、\(q,p\)が\(q,Q\)で表せる変換であるためには、 \[ \det\left|\frac{\partial\, Q_i(q,p,t)}{\partial\, p_j}\right|\ne 0 \] であればよい(定理1-5陰関数定理の系参照)。
\(q,Q\)は当然\(q,p\)で表せる。だから\(q,Q\)と\(q,p\)は逆変換可能な変換だということである。そして\(q,Q\)と\(Q,P\)も逆変換可能な変換だと言える(図5-5参照)。すなわち、座標空間が\(q,Q\)で表せるということである。 まとめると
図5-5
補題5-1 \(q,p\)が\(q,Q\)で表せるなら、\(q,Q\)から\(q,p\)の変換も\(q,Q\)から\(Q,P\)の変換も逆変換可能な変換である。
そして定理1-8を適応すると、 \(q,p\)が\(q,Q\)で表せるなら、\(q,Q,\dot{q},\dot{Q}\)から\(q,p,\dot{q},\dot{p}\)の変換も逆変換可能な変換であると言える。 だから式(\ref{s62})、すなわち\(\mathcal{L}'=L+\frac{dF}{dt}\)は変数\(q,Q,\dot{q},\dot{Q},t\)で表すことができる。そして定理1-9を適応すると、
\(\mathcal{L}'=L+\frac{dF}{dt}\)が変数\(q,Q,\dot{q},\dot{Q},t\)について恒等式になることと、変数\(q,p,\dot{q},\dot{p},t\)について恒等式になることは同値である。
と言える。そこで\(q,Q,\dot{q},\dot{Q},t\)についての恒等式になるような条件を求めよう。母関数\(F\)を\(q,Q,t\)で表して時間微分すると 式(\ref{s62})は \begin{equation} \sum_i P_i\dot{Q}_i-K=\sum_i p_i\dot{q}_i-H+\sum_i\frac{\partial\, F}{\partial\, q_i}\,\dot{q}_i+\sum_i \frac{\partial\, F}{\partial\, Q_i}\,\dot{Q}_i+\frac{\partial\, F}{\partial\, t} \label{mo1} \end{equation} となる。もし \[ P_i=\frac{\partial\, F(Q.q,t)}{\partial\, Q_i} \qquad\qquad -p_i=\frac{\partial\, F(Q.q,t)}{\partial\, q_i} \] \[ -K=-H+\frac{\partial\, F(Q,q,t)}{\partial\, t} \] が変数\(q,Q,t\)の恒等式になるなら 式(\ref{mo1})は\(q,Q,\dot{q},\dot{Q},t\)についての恒等式になる。だから\(Q,P,\dot{Q},\dot{P},t\)の恒等式にもなる。よって\(q,p,H\to Q,P,K\)は正準変換となる。以上、まとめると
定理5-8
1. 変換\(q,p\to Q,P\)は逆変換可能であり、
2, かつ、変換\(q,p\to Q,P\)は変換\(q,Q\to q,p\)が存在するような変換である。
3.
\begin{equation}
P_i=\frac{\partial\, F(Q.q,t)}{\partial\, Q_i}
\qquad\qquad
-p_i=\frac{\partial\, F(Q.q,t)}{\partial\, q_i}
\label{mo2c}
\end{equation}
が\(q,Q\)の恒等式になる。
4.
\begin{equation}
K=H-\frac{\partial\, F(Q,q,t)}{\partial\, t}
\label{mo3c}
\end{equation}
が\(q,Q\)の恒等式になる。
このとき\(Q,P,K\)は正準方程式を満たす。すなわち\(q,p,H\to Q,P,K\)は正準変換となる。
例題5-5
例題5-3でも示したように
\begin{equation}
Q=-p-qt
\qquad\qquad
P=q
\label{qq1c}
\end{equation}
\[
H=q\qquad\qquad K=P-\frac{P^2}{2}
\]
\[
F=-qp-\frac{1}{2}q^2t
\]
とすれば
\[
\mathcal{L}'=\mathcal{L}+\frac{dF}{dt}
\]
を満たすことを示した。この\(q,p,H\to Q,P,K\)の変換と\(F\)が
式(\ref{mo2c})(\ref{mo3c})を満たしていることを確かめよ。
【解】まず、この定理5-8の2が可能かを確認しよう。\(q,p\)を\(q,Q\)で表すと \[ q=q \qquad\qquad p=-qt-Q \] となるので可能である。 次に式(\ref{mo2c})を確かめよう。 この式を使って\(F\)から\(p\)を消去すると \begin{eqnarray} F&=&-q(-qt-Q)-\frac{1}{2}q^2t\notag\\ &=&\frac{1}{2}q^2 t+qQ\notag \end{eqnarray} となる。だから \[ \frac{\partial\, F}{\partial\, Q}=q\qquad\qquad \frac{\partial\, F}{\partial\, q}=qt+Q \] である。一方、変換式(\ref{qq1c})を使って、\(p,P\)を\(q,Q\)で表すと \[ P=q\qquad\qquad p=-qt-Q \] である。よって式(\ref{mo2c})が成り立っていることがわかる。最後に式(\ref{mo3c})が成り立っていることを確かめよう。 \[ H-\frac{\partial\, F(q,Q,t)}{\partial\, t}=q-\frac{1}{2}q^2 \] である。一方\(K\)を\(q,Q\)で表すと \begin{eqnarray} K&=&P-\frac{P^2}{2}\notag\\ &=&q-\frac{q^2}{2}\notag \end{eqnarray} である。よって式(\ref{mo3c})が成り立っていることが確かめられた。だからこの変換は正準変換になると言えるわけである。【解答終】
定理5-8を使って、与えられた母関数\(F\)から正準変換を作り出す方法と与えられたKから正準変換を作り出す方法を示そう。定理1-6から次のことが言える。
補題5-2 関数\(F(q,Q,t)\)が \begin{equation} \det\left|\frac{\partial\,^2 F}{\partial\, Q_j\,\partial\, q_i}\right|\ne 0 \label{bbk0} \end{equation} を満たすなら、 \begin{equation} \frac{\partial\, F(q,Q,t)}{\partial\, Q_i}=P_i \label{bbk1} \end{equation} \begin{equation} \frac{\partial\, F(q,Q,t)}{\partial\, q_i}=-p_i \label{bbk2} \end{equation} の陰関数から変換\(q,p\to Q,P\)を定めることができ、それは逆変換可能である。
では、準備ができたので母関数\(F\)から正準変換を作る方法を述べよう。
定理5-9 母関数\(F\)から正準変換を作る
1. \(F(q,Q,t)\)は
\begin{equation}
\det\left|\frac{\partial\,^2 F}{\partial\, Q_j\,\partial\, q_i}\right|\ne 0
\label{bk0}
\end{equation}
を満たし、
2. 変換\(q,p\to Q,P\)を
\begin{equation}
\frac{\partial\, F(q,Q,t)}{\partial\, Q_i}=P_i
\qquad\qquad
\frac{\partial\, F(q,Q,t)}{\partial\, q_i}=-p_i
\label{df2}
\end{equation}
の陰関数から定め、
3. \(K\)を
\begin{equation}
K\equiv H\left(q,p,t\right)-\frac{\partial\, F(q,Q,t)}{\partial\, t}
\label{dai10}
\end{equation}
と定め、
4. 2を使ってこの式の\(q,p\)を消去し\(K\)を\(Q,P,t\)で表す。
このとき
\(Q,P,K\)は正準方程式を満たす。すなわち\(q,p,H\to Q,P,K\)は正準変換となる。
【証明】定理5-8の条件を満たしていることを確認すればよい。
定理5-8の1:式(\ref{bk0})が成り立つので補題5-2より逆変換可能といえる。
定理5-8の2:ここでの2から\(p\)が\(Q,q\)で表わせているので\(q,p\)は\(q,Q\)で表せる。
定理5-8の3:ここでの2そのままである。
定理5-8の4:式(\ref{dai10})で\(K\)を定理5-8の4が成り立つように決めているのだから成り立つ。【証明終】
例題5-6 母関数\(F=qQ+qt\)、\(H=q^2\)として、これから正準変換となる ように\(q,p\)から\(Q,P\)への変換と\(K\)をもとめよ。
【解】 式(\ref{df2})をこれに適用すると \[ q=P\qquad\qquad Q+t=-p \] これから変換\(q,p\to Q,P\)は \[ Q=-p-t\qquad P=q \] となる。又式(\ref{dai10})を適用すると \begin{eqnarray} K&=&q^2-q\notag\\ &=&P^2-P\notag \end{eqnarray} となる。【解答終】
次に与えられた\(K\)から正準変換を作る方法を示そう。
定理5-10 与えられた\(K\)から正準変換を作る。
\(K\left(Q,\frac{\partial\, F}{\partial\, Q},t\right)\)は\(K(Q,P,t)\)の\(P_j\)のところに\(\frac{\partial\, F(q,Q,t)}{\partial\, Q_i}\)を代入したもの。同じく\(H\left(q,-\frac{\partial\, F}{\partial\, q},t\right)\)は\(H(q,p,t)\)の\(p_i\)のところに\(-\frac{\partial\, F(q,Q,t)}{\partial\, q_i}\)を代入したものとする。
1. \(F(q,Q,t)\)は偏微分方程式
\begin{equation}
K\left(Q,\frac{\partial\, F}{\partial\, Q},t\right)=H\left(q,-\frac{\partial\, F}{\partial\, q},t\right)-\frac{\partial\, F(q,Q,t)}{\partial\, t}
\label{dai10c}
\end{equation}
の解である。
2. そして\(F(q,Q,t)\)は
\begin{equation}
\det\left|\frac{\partial\,^2 F}{\partial\, Q_j\,\partial\, q_i}\right|\ne 0
\label{bk0d}
\end{equation}
を満たす
3. そして
\begin{equation}
\frac{\partial\, F(q,Q,t)}{\partial\, Q_i}=P_i
\qquad\qquad
\frac{\partial\, F(q,Q,t)}{\partial\, q_i}=-p_i
\label{bk2}
\end{equation}
の陰関数から変換\(q,p\to Q,P\)を定める。
このとき
\(Q,P,K\)は正準方程式を満たす。すなわち\(q,p,H\to Q,P,K\)は正準変換となる。
【証明】定理5-8の条件を満たしていることを確認すればよい。
定理5-8の1:ここでの2が成り立つので補題5-2を使うと逆変換可能といえる。
定理5-8の2:ここでの3から\(p\)が\(Q,q\)で表わせているので\(q,p\)は\(q,Q\)で表せる。
定理5-8の3:ここでの3の陰関数から変換\(q,p\to Q,P\)を定めるということは、当然成り立つ。
定理5-8の4:式(\ref{dai10c})を満たしているということは、式(\ref{dai10c})は\(q,Q,t\)についての恒等式になっているということである。定理5-8の4はある変数系\(q,p,t\)でもいいし\(Q,P,t\)でもよいし\(q,Q,t\)でもいいので、それで恒等式になるという意味である。だから\(q,Q,t\)で恒等式なら成り立つのである。
【証明終】
今は、変換は\(q,p\)が\(q,Q\)で表せる場合に限定していたが、\(q,Q\)で表せないときもある。その場合の条件も記述したいが本筋から離れるので付録Cとした。
例題5-7 \[ H=q\qquad K=P \] のとき、偏微分方程式式(\ref{dai10c})を解いて、\(K,Q,P\)が正準方程式を満たすような変換\(q,p\to Q,P\)を求めよ。
【解答】 この場合偏微分方程式(\ref{dai10c})は \[ \frac{\partial\, F}{\partial\, Q}=q-\frac{\partial\, F}{\partial\, t} \] となる。この解として\(F=qQ\)がある。そしてこの\(F\)は \[ \frac{\partial\,^2 F}{\partial\, Q\,\partial\, q}=1 \] なので、式(\ref{bk0d})を満たしている。そして式(\ref{bk2})より \[ q=P\qquad Q=-p \] を得る。だから変換\(q,p\to Q,P\)は \[ Q=-p \qquad\qquad P=q \] と求まる。【解答終】
5-5節 ハミルトンヤコビの方程式の導出
さて、今式(\ref{dai10c})で\(H=0\)の場合を考えよう。 すると式(\ref{dai10c})は \begin{equation} K\left(Q,\frac{\partial\, F}{\partial\, Q},t\right)+\frac{\partial\, F(q,Q,t)}{\partial\, t}=0 \label{ddai10} \end{equation} となる。 \(H=0\)で、\(q,p\)は\(H\)に対して正準方程式を満たすわけだから、\(q\)も\(p\)も時間に依存しない定数となる。だから \[ \frac{\partial\, F(q,Q,t)}{\partial\, Q_i}=P_i \qquad\qquad \frac{\partial\, F(q,Q,t)}{\partial\, q_i}=-p_i \] の陰関数から求めた\(Q,P\)は正準方程式のいわゆる解になる。この偏微分方程式(\ref{ddai10})をハミルトンヤコビの方程式という。 変換を図形的に表すと図5-6のようになる。\(q,p\)は時間経過しても変化しない。
今述べたことを通常の文献に合わせた記号に改め、記号を整理してまとめよう。\(q_i,p_i\)は時間に依存しない定数なので\(\alpha_i,-\beta_i\)とする。そして\(K,Q,P\)を\(H,q,p\)と書き改めよう。\(F\)は\(S\)と改める。その記号で以下のことが言える。
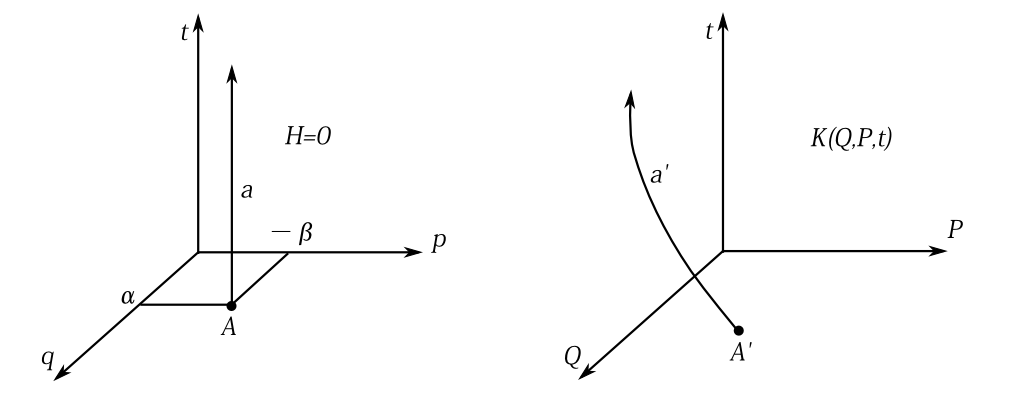
図5-6
定理5-11 ハミルトニアン\(H(q,p,t)\)に対して、未知関数\(S(q,\alpha,t)\)についての偏微分方程式 \[ H\left(q,\frac{\partial\, S}{\partial\, q},t\right)+\frac{\partial\, S}{\partial\, t}=0 \] をハミルトンヤコビの方程式という。\(H\left(q,\partial\, S/\partial\, q,t\right)\)は\(H(q,p,t)\)の\(p_i\)のところに\(\partial\, S/\partial\, q_i\)を代入したもの。さらにSは \[ \det\left|\frac{\partial\,^2 S}{\partial\, q_j\,\partial\, \alpha_i}\right|\ne 0 \] も満たす。 そして、この方程式の解\(S\)を使った式で \[ \frac{\partial\, S(q,\alpha,t)}{\partial\, q_i}=p_i\qquad\qquad\frac{\partial\, S(q,\alpha,t)}{\partial\, \alpha_i}=\beta_i \] の陰関数から求まる\(q,p\)は\(H\)に対して正準方程式 \[ \frac{\partial\, H}{\partial\, q_i}=-\dot{p}_i\qquad\qquad \frac{\partial\, H}{\partial\, p_i}=\dot{q}_i \] を満たす。
5-6節 まとめ
正準変換とは\(q,p,H\)が正準方程式を満たしているとき、\(q,p\to Q,P\)と変数変換して、\(H\to K\)と変換して、その変換によって\(Q,P,K\)が正準方程式を満たすような変換である。簡単に言えば微分方程式の変数変換である。この定義は世間一般での正準変換の定義とは異なることに注意。範囲が広いのである。
任意の変換\(q,p\to Q,P\)に対して\(Q,P\)と正準方程式を満たすような\(K\)が必ず存在するわけではないが(定理5-1)。しかし与えられた\(K\)に対して、\(Q,P,K\)が正準方程式を満たすような変換\(q,p\to Q,P\)は必ずある(定理5-2)。それは \(q,p,H\)系と\(Q,P,K\)系の解軌道を対応させればよいからである。 このことから、正準変換の逆変換も正準変換になると言える。又、正準変換を続けて行っても正準変換になるので、正準変換は群をなすと言える。
正準変換を実際に作り出す方法として母関数を使った方法がある。それは
\begin{equation}
\mathcal{L}'=\mathcal{L}+\frac{dF}{dt}
\label{ew1}
\end{equation}
を満たせば、正準変換になるというものである。ここで\(\mathcal{L}\)は\(\sum_i p_i\dot{q}_i-H\)のこと。\(F\)を母関数という。その根拠は
1. \(\mathcal{L}\)
に対して\(q,p\)がオイラーの方程式を満たすことと正準方程式は同値(定理5-5)
2. \(q,p,t\)の任意の関数\(F(q,p,t)\)
の時間微分はオイラーの方程式を満たす(定理1-1等式4)。
3. ある系でオイラーの方程式を満たすなら他の系でも満たす。(定理1-3)
である。この(\ref{ew1})式を満たす
正準変換が世間一般での正準変換の定義である。
(\ref{ew1})式を満たす
ことは正準変換のために必要条件ではない(定理5-7)。その証明は付録Bに記した
。
変換\(q,p\to Q,P\)が、\(q,p\)が\(q,Q\)で表せるような変換の場合(他の場合は付録C参照)、式(\ref{ew1})は \begin{equation} P_i=\frac{\partial\, F(q,Q,t)}{\partial\, Q_i} \qquad\qquad -p=\frac{\partial\, F(q,Q,t)}{\partial\, q} \label{ma2} \end{equation} \begin{equation} K-H+\frac{\partial\, F(q,Q,t)}{\partial\, t}=0 \label{ma3} \end{equation} と同値である。そこで与えられた母関数\(F(q,Q,t)\)から式(\ref{ma2})を使って変換\(q,p\to Q,P\) を定め、式(\ref{ma3})から\(K\)を定めて正準変換を作るという方法がある。又、与えられた\(K\)から\(F\)を未知関数とする偏微分方程式 \begin{equation} K\left(Q,\frac{\partial\, F}{\partial\, Q},t\right)=H\left(q,-\frac{\partial\, F}{\partial\, q},t\right)-\frac{\partial\, F(q,Q,t)}{\partial\, t} \label{eew2} \end{equation} を解き、その解\(F\)から式(\ref{ma2})を使って変換\(q,p\to Q,P\)を定めるという方法もある。尚、どちらの場合も式(\ref{ma2})から変換\(q,p\to Q,P\)を定めることができるためには \[ \det\left|\frac{\partial\,^2 F}{\partial\, Q_j\,\partial\, q_i}\right|\ne 0 \] であればよい。式(\ref{eew2})で\(H=0\)とした偏微分方程式をハミルトンヤコビの方程式という。\(H=0\)なので\(q,p\)は時間によらない定数となる。だから式(\ref{ma2})を使って\(Q,P\)を\(q,p,t\)の関数として求めたものは正準方程式 のいわゆる解となる。