第6章 ハミルトンヤコビの方程式
前章でハミルトンヤコビの方程式を導出したが、この章ではその解について考察する。ハミルトンヤコビの方程式というのは具体的な問題について解いてみないとわかった気がしないと思う。いくつか解いていけば、その物理的な意味が感覚的にわかってくると思う。ハミルトンヤコビの方程式から正準方程式の解軌道を求めるというのは実用上は全く役に立たない。しかし、ハミルトンヤコビの方程式の解\(S\)をプランク定数\(\hbar\)で割ったものが、シュレディンガー方程式の解\(\psi\)の位相と近似できる。すなわち \[ \exp\left(i\frac{S}{\hbar}\right)\cong\psi \] とできるということにその意義があると思う。そのように近似できることの証明は最後の第6-14節で述べる。1粒子の系のみを扱うが、多粒子系でもその本質は変わらないと思う。 概要としてはまずハミルトンヤコビの方程式の解から正準方程式の解が得られることを証明した。具体例としては直交座標と平面極座標でのハミルトンヤコビの方程式の解と軌道の性質について調べた。常にハミルトンヤコビの方程式の解が波動関数の位相と関係あるということを前提として説明した。ハミルトンヤコビの方程式の解の図形的な側面を個々の場合で調べた。具体例を考えながらハミルトンヤコビの方程式の解の一般的な特徴を述べるという帰納的な方法を取った。ハミルトンヤコビの方程式というのは1階偏微分方程式であり、その一般論というのがあるようだが、私自身その知識がないので扱わない(注 2022年10月追記:筆者の個人的な話だが、その後、スミルノフ高等数学教程9巻から、1階偏微分方程式についての知識を得た。このテキストで扱っているハミルトンヤコビの方程式の解というのは、エネルギーの等しい軌道群が得られる解だけである。正準方程式を解くという観点からは、それで十分だと思う。) 。ハミルトンヤコビの方程式は不変方程式であり、その解が不変量であることを示した。またハミルトンヤコビの方程式の解とラグランジアンの関係、ハミルトンヤコビの方程式の解の等高線と軌道が直交すること、等高線の間隔は\(p\)に逆比例すること、近似波動関数の群速度が古典軌道の速度と一致していること、角運動量の量子化などについて述べた。
6-1節 ハミルトンヤコビの方程式の解から正準方程式の解が得られること
前章でハミルトンヤコビの方程式を導出し、その解から正準方程式の解が得られることを示した。しかしその導出は長く紆余曲折したものであった。歴史的にはそうやってハミルトンヤコビの方程式を見つけたのだろうが決してわかりやすいものではない。そこでこの章の初めにハミルトンヤコビの方程式の解から正準方程式の解が得られるということを簡明な方法で証明しよう。そうすれば前章を飛ばした読者にも役立とう。
定理6-1 ハミルトンヤコビの方程式は未知関数\(S\)についての偏微分方程式 \begin{equation} H\left(q,\frac{\partial\, S}{\partial\, q},t\right)+\frac{\partial\, S}{\partial\, t}=0 \label{ar1} \end{equation} である。\(H\)は系のハミルトニアンである。\(H\left(q,\partial\, S/\partial\, q,t\right)\)は\(H(q,p,t)\)の\(p_i\)のところに\(\partial\, S/\partial\, q_i\)を代入したものである。\(S\)は\(q_i,\alpha_i,t\)の関数である。\(q_i\)と\(\alpha_i\)の個数は等しい。例えば\(q\)が2個、\(q_1,q_2\)なら、\(\alpha\)も\(\alpha_1,\alpha_2\)と2個あるいうことである。\(\alpha_i\)は\(t\)に依存しない定数である。ハミルトンヤコビの方程式の解\(S\)から \begin{equation} \frac{\partial\, S(q,\alpha,t)}{\partial\, q_i}=p_i \label{ar2} \end{equation} \begin{equation} \frac{\partial\, S(q,\alpha,t)}{\partial\, \alpha_i}=\beta_i \label{ar3} \end{equation} という式を作る。 \(\beta_i\)は\(t\)に依存しない定数である。そして\(S\)は式(\ref{ar1})と共に \begin{equation} \det\left|\frac{\partial\,^2 S}{\partial\, q_j\,\partial\, \alpha_i}\right|\ne 0 \label{ar4} \end{equation} も満たしていればならないとする。そうすれば定理1-6より、式(\ref{ar2}),(\ref{ar3})の陰関数として\(q,p\)が\(\alpha,\beta,t\)の関数として求まり、その\(q_i,p_i\)は正準方程式 \[ \frac{\partial\, H}{\partial\, p_i}=\dot{q}_i \qquad\qquad \frac{\partial\, H}{\partial\, q_i}=-\dot{p}_i \qquad(i=1,\cdots,k) \] を満たす。\(\alpha_i,\beta_i\)を正準定数と呼ぶことにする。
【証明】少し長く冗長な定理となってしまったが、ここで主張していることは \(S\)が式(\ref{ar1})を満たし、\(\alpha,\beta\)が時間に依存しないなら、式(\ref{ar2})、式(\ref{ar3}) の陰関数から求まった\(q,p\)が正準方程式 \[ \frac{\partial H(q,p,t)}{\partial p_i}=\dot{q}_i \qquad\qquad \frac{\partial H(q,p,t)}{\partial q_i}=-\dot{p}_i \] を満たすということである。すなわち、\(q,p\)は 式(\ref{ar2})、式(\ref{ar3}) の陰関数から\(\alpha,\beta,t\)の関数として求まり、 それを時間で微分すれば\(\dot{p},\dot{q}\)も\(\alpha,\beta,t\)の関数として求まる。 そして\(\frac{\partial H(q,p,t)}{\partial p},-\frac{\partial H(q,p,t)}{\partial q}\)も、その\(q,p\)を使えば\(\alpha,\beta,t\)の関数として求まる。それが一致するということである。 すなわち正準方程式の左辺と右辺が\(\alpha,\beta,t\)の恒等式になるということである。 定理1-6より、\(\alpha,\beta\)から\(q,\alpha\)への変換は互いに逆変換可能なので定理1-7より \(q,\alpha,t\)の恒等式であることが示されればよいことになる。もちろん\(q,p,t\)の恒等式であることを示してもいいのだが、ハミルトンヤコビの方程式の解が\(q,\alpha,t\)の関数として表されているので\(q,\alpha,t\)の方が楽なのである。そういうわけで\(q,\alpha,t\)の恒等式であることを証明しよう。
式(\ref{ar3}) を時間で全微分すると \begin{equation} \sum_j \frac{\partial\, ^2 S(q,\alpha,t)}{\partial\, q_j\,\partial\, \alpha_i}\dot{q}_j+\frac{\partial\, ^2 S(q,\alpha,t)}{\partial\, t\,\partial\, \alpha_i}=0 \label{ar5} \end{equation} が成り立つ。これを\(\dot{q}\)について解けば\(\dot{q}\)が\(q,\alpha,t\)で表せるわけである。ところでハミルトンヤコビの方程式(\ref{ar1})での\(H\Big(q,\frac{\partial S}{\partial q},t\Big)\)というのは\(H(q,p,t)\)の\(p_j\)のところに\(\frac{\partial S}{\partial q_j}\)を代入したものであった。そして\(p\)自体も\(p_j=\frac{\partial S(q,\alpha,t)}{\partial q_j}\)という式で\(q,\alpha,t\)の関数として表されるのであった。だから\(\frac{\partial S(q,\alpha,t)}{\partial q_j}\)を\(p_j(q,\alpha,t)\)と書けば、ハミルトンヤコビの方程式は \begin{equation} H\Big(q,p(q,\alpha,t),t\Big)+\frac{\partial\, S(q,\alpha,t)}{\partial\, t}=0 \label{y1208} \end{equation} と書ける。 これは\(q,\alpha,t\)の恒等式なので、\(\alpha_i\)で偏微分すると \begin{equation} \sum_j \frac{\partial\, p_j(q,\alpha,t)}{\partial\, \alpha_i}\frac{\partial\, H(q,p,t)}{\partial\, p_j} +\frac{\partial\, ^2 S(q,\alpha,t)}{\partial\, \alpha_i\,\partial\, t}=0 \label{ar6} \end{equation} が成り立つ。さて\(\frac{\partial\, ^2 S(q,\alpha,t)}{\partial\, q_j\,\partial\, \alpha_i}=\frac{\partial\, p_j(q,\alpha,t)}{\partial\, \alpha_i}\)であることを思い出して、式(\ref{ar5})と式(\ref{ar6}) を見比べると\(\dot{q}_j\)の部分が\(\frac{\partial\, H}{\partial\, p_j}\)に置き換わっただけである。だからそれぞれの式で \(\dot{q}_j\)と\(\frac{\partial\, H}{\partial\, p_j}\)について解くことができるならば、解は同じものになる。そして条件式(\ref{ar4}) より解くことは可能である。だから正準方程式\(\frac{\partial\, H}{\partial\, p_j}=\dot{q}_j\)の両辺を\(q,\alpha,t\)で表せばそれは\(q,\alpha,t\)の恒等式になる。
もう1つの方を証明しよう。式(\ref{ar2})を時間で全微分すると \begin{equation} \sum_j \frac{\partial\, ^2 S(q,\alpha,t)}{\partial\, q_j\,\partial\, q_i}\dot{q}_j+\frac{\partial\, ^2 S(q,\alpha,t)}{\partial\, t\,\partial\, q_i}=\dot{p}_i \label{ar7} \end{equation} が成り立つ。一方ハミルトンヤコビの方程式(\ref{y1208})は\(q,\alpha,t\)の恒等式なので\(q_i\)で偏微分すると \begin{equation} \frac{\partial\, H(q,p,t)}{\partial\, q_i} +\sum_j\frac{\partial\, p_j(q,\alpha,t)}{\partial\, q_i} \frac{\partial\, H(q,p,t)}{\partial\, p_j} +\frac{\partial\, ^2 S(q,\alpha,t)}{\partial\, q_i\,\partial\, t}=0 \label{ar8} \end{equation} が成り立つ。さて式(\ref{ar7})と式(\ref{ar8})を比べると、\(\frac{\partial\,^2 S(q,\alpha,t)}{\partial\, q_j\,\partial\, q_i}=\frac{\partial\, p_j(q,\alpha,t)}{\partial\, q_i}\)であり、\(\frac{\partial\, H}{\partial\, p_j}=\dot{q}_j\)であるので、 \(\frac{\partial H(q,p,t)}{\partial q_i}=-\dot{p}_i\)の両辺を\(q,\alpha,t\)で表せばそれは\(q,\alpha,t\)の恒等式になる。 【証明終】
ある時間での系の状態は\(q\)と\(\dot{q}\)を定めれば決まる。\(q,\dot{q}\)から\(q,p\)への変換は逆変換可能なので、系の状態は\(q,p\)を定めても決まる。又、定理1-6より、\(\alpha,\beta\)から\(q,\alpha\)への変換は互いに逆変換可能なのだから
ある時間での系の状態は\(q\)と\(\alpha\)を指定すれば決まる。
と言える。大ざっぱに言えばラグランジュ方程式は系の状態を\(q,\dot{q}\)で指定するもの、正準方程式は系の状態を\(q,p\)で指定するもの、ハミルトンヤコビの方程式は系の状態を\(q,\alpha\)で指定するものと言える。
6-2節 1次元自由粒子
最も簡単な例として、1次元自由粒子の場合を考えよう。1次元自由粒子のハミルトニアンは \[ H=\frac{p^2}{2m} \] である。だからハミルトンヤコビの方程式は\(p\)のところに\(\frac{\partial\, S}{\partial\, x}\)を代入した \begin{equation} \frac{1}{2m}\left(\frac{\partial\, S(x,\alpha,t)}{\partial\, x}\right)^2+\frac{\partial\, S(x,\alpha,t)}{\partial\, t}=0 \label{kai1} \end{equation} である。この偏微分方程式を満たす\(S(x,\alpha,t)\)を求めればよいわけである。そこで \begin{equation} S=-Et+\alpha x+c \label{kai2} \end{equation} とおいてみよう。\(E\)と\(c\)は\(x,t\)に依存しない定数である。これを式(\ref{kai1})に代入すると、 \begin{equation} \frac{\alpha^2}{2m}=E \label{kai3} \end{equation} が成り立つなら式(\ref{kai2})はハミルトンヤコビの方程式の解になることがわかる。だから \begin{equation} S=-\frac{\alpha^2}{2m}t+\alpha x+c \label{kai4} \end{equation} が1次元自由粒子のハミルトンヤコビの方程式の解である。そして\(S\)の満たすべき条件式(\ref{ar4})が満たされていることを確認しなければならない。今の場合\(\det\left|\frac{\partial\,^2 S}{\partial\, q_j\,\partial\, \alpha_i}\right|\)は1行1列の行列で成分は \[ \frac{\partial\, ^2 S}{\partial\, x \,\partial\, \alpha}=1 \] である。行列式の値は1であり、 条件式(\ref{ar4})は満たされている。 次にこの\(S\)から\(x\)と\(p\)を時間の関数として求めてみよう。前章で述べたように \[ \frac{\partial\, S}{\partial\, \alpha}=\beta\qquad\qquad \frac{\partial\, S}{\partial\, x}=p \] から\(x,p\)を求める。そうすると \[ -\frac{\alpha}{m}t+x=\beta\qquad\qquad \alpha=p \] を得る。よって \[ x=\frac{\alpha}{m}t+\beta \qquad\qquad p=\alpha \] と求まる。これがハミルトニアン\(H=p^2/2m\)のときの正準方程式の解である。
6-3節 正準定数について
さて、もう少し1次元自由粒子の例を考察して理解を深めよう。解は \[ S=-\frac{\alpha^2}{2m}t+\alpha x+c \] であったが、正準定数\(\alpha\)の役は、この式の\(\alpha\)でなくてもよい。正準定数としての\(\alpha\)の役割とは、\(\frac{\partial\, S}{\partial\, \alpha}=\beta\)に使う定数のことである。式(\ref{kai3})に立ち戻って、(条件式(\ref{ar4})さえ満たしていれば、)\(E\)をその役としても良いわけである。この場合、解\(S\)は \[ S=-E\;t+\sqrt{2mE}\;x+c \] と表される。条件式(\ref{ar4})は今の場合 \[ \frac{\partial\, ^2 S}{\partial\, x \,\partial\, E}\ne 0 \] なので満たされている。 そして \[ \frac{\partial\, S}{\partial\, E}=\beta\qquad\qquad \frac{\partial\, S}{\partial\, x}=p \] より \[ -t+\frac{m}{\sqrt{2mE}}x=\beta\qquad\qquad\sqrt{2mE}=p \] を得る。これから \[ x=\frac{\sqrt{2mE}}{m}t+\frac{\sqrt{2mE}}{m}\beta \qquad\qquad p=\sqrt{2mE} \] と求まる。
ところで、ハミルトンヤコビの方程式の解(\ref{kai4})の \[ S=-\frac{\alpha^2}{2m}t+\alpha x+c \] で、この\(c\)を正準変数としての定数とできるだろうか。この場合 \[ \frac{\partial\, ^2 S}{\partial\, x \,\partial\, c}=0 \] となり、条件式(\ref{ar4})は満たされないので、だめなのである。実際 \[ \frac{\partial\, S}{\partial\, c}=\beta \qquad\qquad \frac{\partial\, S}{\partial\, x}=p \] より \[ 1=\beta \qquad\qquad \alpha=\beta \] となる。これでは\(x,p\)が求まらないのである。
一般に
\(\alpha\)が正準定数で、\(\alpha\to\alpha'\)と変換したとき、\(\det\left|\frac{\partial\,\alpha'_j}{\partial\,\alpha_i}\right|\ne 0\)なら、\(\alpha'\)も正準定数となる。
【証明】\(\det\left|\frac{\partial\,\alpha'_j}{\partial\,\alpha_i}\right|\ne 0\)なら \[ \det\left|\frac{\partial\,\alpha_j}{\partial\,\alpha'_i}\right|\ne 0 \] である。そして \[ \frac{\partial\,^2 S}{\partial\,\alpha'_i\partial\, q_j}=\sum_k\frac{\partial\, \alpha_k}{\partial\, \alpha'_i}\frac{\partial\, ^2 S}{\partial\, \alpha_k \partial\, q_j} \] である。だから \[ \det\left|\frac{\partial\,^2 S}{\partial\,\alpha'_i\partial\, q_j}\right| = \det\left|\frac{\partial\, \alpha_k}{\partial\, \alpha'_i}\right|\det\left|\frac{\partial\, ^2 S}{\partial\, \alpha_k \partial\, q_j}\right| \ne 0\] となる。だから\(\alpha'\)も正準定数となる。【証明終】
6-4節 時間を含まないハミルトニアンのハミルトンヤコビの方程式
さて今のようにハミルトニアンが時間を含まない場合(基本的には時間を含まない場合しか扱わないのだが)、\(E\)を定数として \[ S(q,\alpha,t)=-Et+W(q,\alpha) \] とおくと ハミルトンヤコビの方程式は \begin{equation} H\left(q,\frac{\partial\, W(q,\alpha)}{\partial\, q}\right) =E \label{kai7} \end{equation} となる。この\(E\)というのはハミルトンヤコビの方程式から求められた軌道のエネルギーに対応することになる。それは \(\partial\, w/\partial\, q=p\)だからである。
6-5節 1次元でポテンシャルがある場合
次に1次元でポテンシャルがある場合のハミルトンヤコビの方程式を考えよう。 \[ H=\frac{p^2}{2m}+V(x) \] なのでハミルトンヤコビの方程式は\(S=-Et+W(x,\alpha)\)とおいて \[ \frac{1}{2m}\left(\frac{\partial\, W}{\partial\, x}\right)^2+V(x)=E \] である。これから \begin{equation} \frac{\partial\, W}{\partial\, x}=\pm\sqrt{2m[E-V(x)]} \label{po1} \end{equation} であればよいわけである。だから \[ W=\pm \int^x\sqrt{2m[E-V(x')]}dx' \] であれば良く、 \[ S=-E\;t\pm \int^x\sqrt{2m[E-V(x')]}dx' \] と解が求まる。この場合において\(E\)をそのまま正準定数としてみよう。このとき \[ \frac{\partial\,^2 S}{\partial\, E\partial\, x}=\frac{m}{\sqrt{2m[E-V(x)]}} \] なので、\(E-V(x)= 0\)でない領域で正準定数として使える。 \[ \frac{\partial\, S}{\partial\, E}=\beta \qquad\qquad \frac{\partial\, S}{\partial\, x}=p \] より \[ -t\pm\int^x\frac{m}{\sqrt{2m[E-V(x')]}}dx'=\beta \qquad\qquad \sqrt{2m[E-V(x)]}=p \] が得られる。 尚、ハミルトンヤコビの方程式の解の定義域は式(\ref{po1})より、\(E-V(x)\ge 0\)という領域に限られる。
6-6節 2次元自由粒子
解と軌道
次に自由粒子の2次元の場合を考える。解き方は1次元の場合と全く同じである。直交座標でハミルトニアンは \[ H=\frac{1}{2m}\left(p_x^2+p_y^2\right) \] なので時間を含まないハミルトンヤコビの方程式(\ref{kai7})は \[ \frac{1}{2m}\left[\left(\frac{\partial\, W}{\partial\, x}\right)^2+\left(\frac{\partial\, W}{\partial\, y}\right)^2\right] =E\] である。 \[ W=\alpha_x x+\alpha_y y \] として代入すると \[ \frac{1}{2m}(\alpha_x^2+\alpha_y^2)=E \] であればよい。だからハミルトンヤコビの方程式の解は \begin{equation} S=-\frac{1}{2m}(\alpha_x^2+\alpha_y^2)t+\alpha_x x+\alpha_y y \label{2ji} \end{equation} である。 \[ \frac{\partial\, S}{\partial\, \alpha_x}=\beta_x, \quad \frac{\partial\, S}{\partial\, x}=p_x, \quad \frac{\partial\, S}{\partial\, \alpha_y}=\beta_y, \quad \frac{\partial\, S}{\partial\, y}=p_y \] より \[ -\frac{\alpha_x}{m}t+x=\beta_x, \qquad \alpha_x=p_x \qquad -\frac{\alpha_y}{m}t+y=\beta_y, \qquad \alpha_y=p_y \] を得る。よって正準方程式の解は \[ x=\frac{\alpha_x}{m}t+\beta_x, \qquad p_x=\alpha_x \qquad y=\frac{\alpha_y}{m}t+\beta_y, \qquad p_y=\alpha_y \] と求まる。尚、2次元自由粒子のハミルトンヤコビの方程式の解はもう1つある (注 2022年10月追記:ハミルトンヤコビの方程式の解は無限にあるが、ここでは代表的なものがもう1つある程度の意味と考えてもらいたい。) 。それは6-9節で簡単に紹介する。
軌道と\(S\)の図形関係
さて、今から2次元自由粒子の\(S\)と軌道の図形的な関係を見よう。 まず\(S\)の空間部分\(W(x,y,\alpha_x,\alpha_y)=\alpha_x x+\alpha_y y\)について考える。\(\alpha_x,\alpha_y\)が与えられれば、すなわち運動量が与えられれば、\(W\)は位置座標\(x,y\)のみの関数となる。そこで\(W\)が一定となる線、いわゆる等高線を、\(W\)の変化が等しい間隔ごとに描いてみよう。
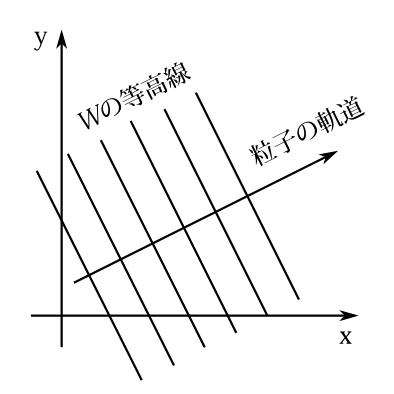
図6-1 \(W=2x+y\)としたときの軌道と\(W\)の等高線の関係
\(W=\alpha_x x+\alpha_y y\)で例えば\((\alpha_x,\alpha_y)=(2,1)\)とし\(W=0\)として、その線を描き、次に\(W=1,W=2\)と変えて、その線を描けば良いわけである。図6-1がその様子である。ところで等高線の方向の変位ベクトル\((\Delta x,\Delta y)\)は、それに対応する\(W\)の変化\(\Delta W\)は\(0\)だというのだから \[ \frac{\partial\, W}{\partial\, x}\Delta x+\frac{\partial\, W}{\partial\, y}\Delta y=0 \] である。すなわち等高線と\(\nabla W=\left(\frac{\partial\, W}{\partial\, x},\frac{\partial\, W}{\partial\, y}\right)\)は直交する。又 \[ \left(\frac{\partial\, W}{\partial\, x},\frac{\partial\, W}{\partial\, y}\right)=(p_x,p_y) \] なので、等高線と\((p_x,p_y)\)を成分とするベクトルは直交する。\((p_x,p_y)\)は軌道の進行方向なので等高線は軌道と直交すると言える (注 2022年10月追記:多粒子系の場合は、個々の粒子の質量が異なれば、運動量は軌道の向きと一致しなくなるので、等高面と軌道が直交するとは言えない。 ) 。等高線と軌道が直交することはポテンシャルがある場合でも成り立つことである。それは今の証明からわかろう。そして、等高線と軌道が直交することは、どの座標でハミルトンヤコビの方程式の方程式を解いた場合でも成り立つことである。その証明は6-12節で述べる。もしシュレディンガーの波動関数\(\psi\)が \[ \psi\cong \exp\left( i\frac{S}{\hbar}\right) \] と近似できるなら、等高線というのは同位相線となるから、同位相線と軌道は直交すると言える。
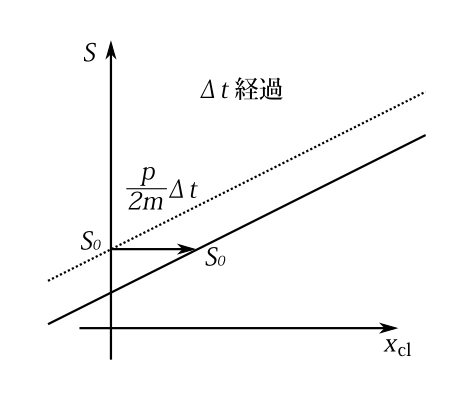
図6-2 一つの軌道をとりだし、その軌道に沿った\(S\)一定の点の動き。点線が最初の\(S\)の値。実線が\(\Delta t\)後の\(S\)の値。Sが一定の点\(S_0\)は\(\frac{p}{2m}\Delta t\)動く。
次に時間を含めて、等高線がどう動くかを見てみよう。そこで粒子の運動方向を\(x_\text{cl}\)軸としてみると、 \begin{equation} S=-\frac{p^2}{2m}t+p\,x_\text{cl} \label{kai71} \end{equation} となる。ここで\(p\)は運動量の大きさ。そして図6-2のように横軸を粒子の進行方向の\(x_\text{cl}\)、縦軸を\(S\)とする。ある瞬間では、\(x\)と\(S\)の関係は図6-2の点線のようであり、それから\(\Delta t\)たつと\(S\)は\(\frac{p^2}{2m}\Delta t\)下がって図6-2の実線になる。\(S\)一定の点がどう動くかというと、式(\ref{kai71})より \[ x_\text{cl}=\frac{p}{2m}t+\frac{S}{p} \] だから\(p/2m\)の速さで動く。すなわち粒子の速さの半分で動くわけである。自由粒子の場合\(\exp\left( i\frac{S}{\hbar}\right)\)はシュレディンガー方程式の解になっている。だから\(S\)一定は、位相が一定ということであり、それが\(p/2m\)の速さで動くということは、位相速度が\(p/2m\)だということである。
6-7節 2次元一様重力場
解と軌道
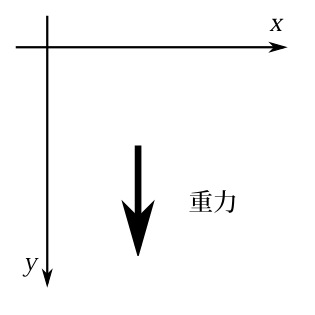
図6-3 下向き=重力の向きに\(y\)軸の正の向きをとる。
次に自由落下粒子のハミルトンヤコビの方程式を解こう。この場合の解\(S\)を研究すれば、他の場合の\(S\)の概要も予想がつく。というのは他のポテンシャルのときでも、狭い領域では力の大きさ、向きは共に一定と考えられるからである。空間を2次元として座標軸は図6-3のように重力の方向に\(y\)軸の正の向きをとると ハミルトニアンは \[ H=\frac{1}{2m}\left(p_x^2+p_y^2\right)-mgy \] となる。だから時間を含まないハミルトンヤコビの方程式は \begin{equation} \frac{1}{2m}\left[\left(\frac{\partial\, W}{\partial\, x}\right)^2+\left(\frac{\partial\, W}{\partial\, y}\right)^2\right] -mgy =E \label{kai91} \end{equation} となる。左辺に\(x\)は現れないので \[ W=\alpha_x x+Y(y) \] とおこう。ここで\(Y(y)\)は\(y\)のみの関数という意味である。これを式(\ref{kai91})に代入すると \[ \frac{1}{2m}\left[\alpha_x^2+\left(\frac{\partial\, Y}{\partial\, y}\right)^2\right] -mgy =E \] となる。だから \[ \frac{dY}{dy}=\pm\sqrt{2m\left(E-\frac{\alpha_x^2}{2m}+mgy\right)} \] であれば良いわけである。ここでの\(\pm\)は\(\frac{dY}{dy}\)が運動量なので、運動量の正負に、今の場合下向きか上向きに対応している。そして \begin{equation} S=-Et+\alpha_x x\pm\int^y \sqrt{2m\left(E-\frac{\alpha_x^2}{2m}+mgy'\right)}dy' \label{koremo} \end{equation} が解である。 さて、\(E\)と\(\alpha_x\)を正準変数としての定数としてもよいが、式を簡単にするために \[ E=E_y+\frac{\alpha_x^2}{2m} \] とおこう。 すると \[ Y=\pm\int^y\sqrt{2m}\sqrt{E_y+mgy'}\;\;dy' \] となる。これを積分すると \[ Y=\pm\frac{2\sqrt{2m}}{3mg}(E_y+mgy)^{\frac{3}{2}} \] となる。 だからハミルトンヤコビの方程式の解\(S\)は
2次元自由落下のハミルトンヤコビの方程式の解
\begin{equation}
S=
-\left(E_y+\frac{\alpha_x^2}{2m}\right)t+\alpha_x x\pm\frac{2\sqrt{2m}}{3mg}(E_y+mgy)^{\frac{3}{2}}
\label{kai95}
\end{equation}
となる。
\(\pm\)とあるのは\(+\)のときも\(-\)のときも解となるという意味である。この\(S\)から軌道を求めよう。
(\(x\)成分)
\(\partial\, S/\partial\, \alpha_x=\beta_x,\,\partial\, S/\partial\, x=p_x\)より
\[
-\frac{\alpha_x}{m}t+x=\beta_x,
\qquad\qquad
\alpha_x=p_x
\]
これから
\[
x=\frac{\alpha_x}{m}t+\beta_x\qquad\qquad
p_x=\alpha_x
\]
(\(y\)成分)
\(\partial\, S/\partial\, E_y=\beta_y,\,
\partial\, S/\partial\, y=p_y
\)
より
\begin{equation}
-t\pm \frac{\sqrt{2m(E_y+mgy)}}{mg}=\beta_y
\qquad\qquad
\pm\sqrt{2m(E_y+mgy)}=p_y
\label{1207}
\end{equation}
右の式を左の式に入れて
\[
p_y=mg(t+\beta_y)
\]
式(\ref{1207})の右の式を自乗して
\[
y=\frac{1}{mg}\left(
\frac{p_y^2}{2m}-E_y
\right)
\]
を得る。
まとめると解軌道は
2次元自由落下の解軌道 \begin{eqnarray} &x=\frac{\alpha_x}{m}t+\beta_x\qquad\qquad &p_x=\alpha_x\notag\\ &y=\frac{1}{mg}\left( \frac{p_y^2}{2m}-E_y \right) \qquad\qquad &p_y=mg(t+\beta_y) \notag \end{eqnarray}
となる。
軌道と\(W\)の図形関係
次にこの\(W\)の等高線と軌道の関係を図示してみよう。まず式(\ref{kai95})での\(\pm\)の\(+\)の場合を図示しよう。これは落下している場合である。 \[ W=\alpha_x x+\frac{2\sqrt{2m}}{3mg}(E_y+mgy)^{\frac{3}{2}} \] を文字を改めて \begin{equation} W=\alpha_x x+\kappa(y+y_0)^{\frac{3}{2}} \label{tt1} \end{equation} としよう。ここで\(\kappa=\frac{2m\sqrt{2g}}{3},\;y_0=E_y/mg\)である。 この式を\(x\)に関して解くと \begin{equation} x=-\frac{\kappa}{\alpha_x}(y+y_0)^{\frac{3}{2}}+\frac{W}{\alpha_x} \label{tt2} \end{equation} となる。\(W\)一定の等高線は \[ x=-\frac{\kappa}{\alpha_x}y^{\frac{3}{2}} \] という曲線を \(y\)方向に\(-y_0\)ずらして\(x\)方向に\(W/\alpha_x\)ずらしたものになる。 図6-4に\(y_0=0\)のときの\(W\)の等高線と軌道の模式図を描いた。等高線の間隔は\(W\)の変化量が等しいように描いてある。 一つ一つの等高線は\(x=-\frac{\kappa}{\alpha_x}y^{\frac{3}{2}}\)の曲線を\(x\)軸方向へ等間隔に平行移動したものである。又、軌道は等高線と直交するので、一つ一つの軌道は、すべて互いに\(x\)軸方向へ平行移動したものになっている。
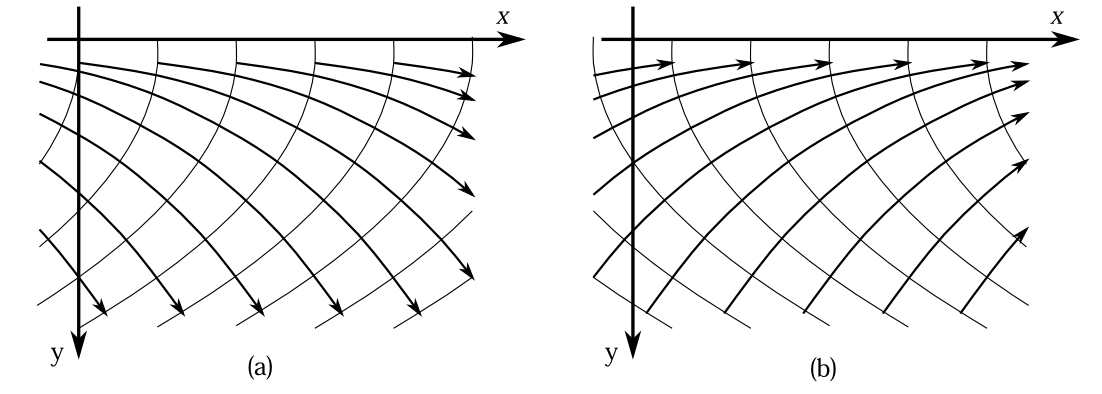
図6-4 自由落下の等高線と軌道線。(a):下降しているとき。(b):上昇しているとき
次に運動方向が上向きの場合の\(S\)の等高線を描こう。それは式(\ref{kai95})で\(\pm\)の\(-\)の方の\(S\)である。だから式(\ref{tt1})(\ref{tt2})はそれぞれ \[ W=\alpha_xx-\kappa(y+y_0)^{\frac{3}{2}} \] \[ x=\frac{\kappa}{\alpha_x}(y+y_0)^{\frac{3}{2}}+\frac{W}{\alpha_x} \] となる。図6-4(b)に\(y_0=0\)のときの等高線と軌道を描いた。等高線は図6-4(a)で\(y\)軸で反転したものになる。
どんなポテンシャルでも狭い領域では力の大きさと向きは一定と考えられるので、そのような領域では図6-4のような\(W\)と軌道の関係が得られるであろう。だから一般に次のことが言えると思う。
仮説6-1 力の大きさと向きが一定と考えられるほどの十分狭い領域では、ハミルトンヤコビの方程式の解\(S\)からなる軌道群は1つの軌道を力の方向に直角にずらしたものの集まりとなる。そして、力の方向の運動量が反転するときは、運動量部分のプラスマイナスを反転させた\(S\)を用いなければならない。
6-8節 位相としての\(S\)について
一般のポテンシャルでのハミルトンヤコビの方程式の解\(S\)の位相としての性質を考察する。すなわちシュレディンガー方程式の波動関数を \[ \psi\cong\exp\left(i\frac{S}{\hbar}\right) \] と近似できるとして、その波動関数の波長、振動数、位相速度、群速度について調べる。 この節の考察は1粒子の系に限定する。\(x_i\)を直交座標とする。正準定数\(\alpha\)は与えられていて変化しないとする。\(x_i,t\)の微小変位\(\Delta x_i,\Delta t\)とそれに対応する\(S\)の変位\(\Delta S\)との関係は、1次まででは \[ \Delta S=\frac{\partial\, S}{\partial\, t}\Delta t+\sum_{i=1}^3\frac{\partial\, S}{\partial\, x_i}\Delta x_i \] である。\(\partial\, S/\partial\, x_i=p_i\)であり、 ハミルトンヤコビの方程式より \(H+\frac{\partial\, S}{\partial\, t}=0\)で\(H=E\)なので\(\frac{\partial\,S}{\partial\, t}=-E\)である。だから \[ \Delta S=-E\Delta t+\sum_{i=1}^3p_i\Delta x_i \] となる。今、変位\(\Delta x_i\)の向きを軌道の動く方向と同じ向きにとる。そしてその大きさを\(\Delta x_\text{cl}\)と書こう。又、運動量の大きさを\(p\)と書くとしよう。軌道の動く方向と運動量の向きは同じなので 、このときは \[ \sum_{i=1}^3p_i\Delta x_i=p \Delta x_{cl} \] となる。だから\(\Delta x_i\)の向きが運動方向と同じときは \[ \Delta S=-E\Delta t+p\Delta x_\text{cl} \] となる。 だから運動方向の等高線の間隔は運動量の大きさ\(p\)に逆比例する。一様重力場の場合、位置が下がるほど運動量は大きくなり、等高線の間隔は狭くなる(図6-4参)。等高線の間隔というのは波長のことなので(正確には波長に比例した長さ)波長は運動量の大きさに逆比例する。 又、軌道方向への\(S\)一定の点の速さは \begin{equation} \frac{E}{p} \label{atosan} \end{equation} となる。\(E\)一定なので、運動量が大きいほど速さが遅くなる。ただ\(E\)の大きさはポテンシャルの0点のとり方によって変わるので、この速さ自体には意味がない。図6-5に自由落下ポテンシャルでの軌道に沿ったS一定の点の動きを書いた。これは図6-4(a)の一つの軌道を取り出しその軌道上でのSと\(\Delta t\)後のSを書いたものである。軌道に沿って運動量は大きくなるので\(S\)の傾きも大きくなる。\(S\)一定の点の速さというのは位相速度のことである。
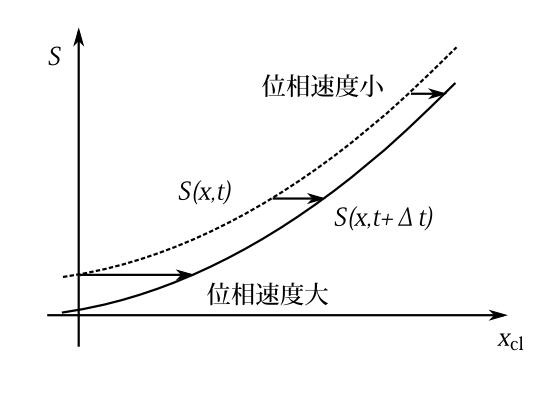
図6-5 図6-4(a)の一つの軌道をとりだし、その軌道に沿った\(S\)一定の点の動き。点線が最初の\(S\)の値。実線が\(\Delta t\)後の\(S\)の値
次に \( \psi\cong\exp\left(i\frac{S}{\hbar}\right) \) とした場合の群速度を考えよう。群速度というのは、方向は同じだが大きさが異なる運動量の波動関数を重ね合わせたときに意味を持つ。位相の変化は \[ \frac{\Delta S}{\hbar}=-\frac{E}{\hbar}\Delta t+\frac{p}{\hbar}\Delta x_\text{cl} \] なので、 角振動数\(w=E/\hbar\)、波数\(k=p/\hbar\)となる。群速度は\(dw/dk\)なので、群速度は \[ \frac{dW}{dk}=\frac{\partial\, E}{\partial\, p}=\frac{\partial\,}{\partial\, p}\left(\frac{p^2}{2m}+V\right) =\frac{p}{m} \] となる。群速度は軌道の速さと一致する。ただこれは近似式で波動関数の群速度が古典軌道の速さと一致していると言っているだけである。ここでの結果をまとめると
定理6-2
1粒子の系では、波動関数\(\psi\)を
\[
\psi\cong\exp\left(i\frac{S}{\hbar}\right)
\]
と近似すると、古典軌道に沿った線上では
1. 波長は運動量に逆比例する
2. 位相速度は\(\frac{E}{p}\)である。
3. 群速度は古典速度に一致する。
となる。
6-9節 平面極座標
中心力場
今までは直交座標でのハミルトンヤコビの方程式を扱ってきたが、それ以外の座標系の例として、2次元中心力場の極座標でのハミルトンヤコビの方程式を考えよう。この場合ハミルトニアンは4章式(16)より
\[
H=\frac{1}{2m}\left(p_r^2+\frac{p_\theta^2}{r^2}\right)+V(r)
\]
である。だから時間を含まないハミルトンヤコビの方程式は
\[
\frac{1}{2m}\left[\left(\frac{\partial\, W}{\partial\, r}\right)^2+\frac{1}{r^2}\left(\frac{\partial\, W}{\partial\, \theta}\right)^2\right]+V(r)
=E
\]
となる。\(H\)に\(\theta\)が含まれないので
\[
W=\alpha_\theta \theta +R(r)
\]
とおく。\(R(r)\)は\(r\)のみの関数という意味。\(R\)は
\[
\frac{\partial\, R}{\partial\, r}=\pm
\sqrt{2m\left(E-\frac{\alpha_\theta^2}{2mr^2}-V\right)}
\]
を満たしていればよい。だからハミルトンヤコビの方程式の解は
\begin{equation}
S=-E\;t+\alpha_\theta \theta\pm \int^r
\sqrt{2m\left(
E-\frac{\alpha_\theta^2}{2mr'^2}-V\right)} \;dr'
\label{kai161}
\end{equation}
となる。\(S\)は
\[
E-\left(\frac{\alpha_\theta^2}{2mr^2}+V\right)\ge 0
\]
の範囲で定義される。この\(S\)から軌道を求めよう。
(\(\theta\)について)
\(\partial\, S/\partial\, \theta=p_\theta,\; \partial\, S/\partial\, \alpha_\theta=\beta_\theta\)より
\begin{equation}
\alpha_\theta=p_\theta
\qquad\qquad
\theta\mp\alpha_\theta\int^r\frac{1}{r'^2\sqrt{2m\left(
E-\frac{\alpha_\theta^2}{2mr'^2}-V\right)}}\;\; dr'=\beta_\theta
\label{tyu1}
\end{equation}
(\(r\)について)
\(\partial\, S/\partial\, r=p_r,\; \partial\, S/\partial\, E=\beta_r\)より
\begin{equation}
\pm\sqrt{2m\left(
E-\frac{\alpha_\theta^2}{2mr^2}-V\right)}=p_r
\qquad
-t\pm\frac{\sqrt{2m}}{2}\int^r\frac{1}{\sqrt{2m\left(
E-\frac{\alpha_\theta^2}{2mr'^2}-V\right)}}\;\; dr'=\beta_r
\label{tyu3}
\end{equation}
となる。実際に積分するのは困難なのでここでやめておく。
次にこのWの等高線と軌道の関係を図示してみよう。 そしてポテンシャルとして万有引力型の\(V=-\frac{k}{r}\)としてみよう。\(k\)は定数。 \(E<0\)なら楕円。\(E=0\)なら放物線。\(E>0\)なら双曲線になることはよく知られたことである。 今\(E<0\)だとして\(W(r,\theta)\)の等高線の概略を描いてみよう。式(\ref{kai161})の\(\pm\)の\(+\)としよう。 これは式(\ref{tyu3})より\(p_r\ge 0\)の場合である。第4章の式(14)で見たとおり、\(p_r=m\dot{r}\)なので、\(\dot{r}\ge 0\)の軌道である。だから、 この\(S\)に含まれるのは、楕円の近日点から遠日点への軌道である。等高線は軌道と直交することを利用して等高線の様子を概観する。近日点と遠日点では\(\dot{r}=0\)なので等高線は半径方向となる。それ以外では\(\dot{r}>0\)なので等高線は図6-6}のようになろう。\(W\)の\(\theta\)への依存は\(\alpha_\theta \theta\)という項からで、線形になっている。だから等高線は\(\Delta W\)を一定の間隔にすると、図6-6のように\(\theta\)方向にずらしたものになる。\(W(r,\theta)\)は\(\theta\)が一周すると元の\(W\)と異なった値となる。

図6-6 楕円軌道群での\(W\)の等高線と軌道の模式図
1つの\(S\)からなる軌道群は、1つの軌道を角\(\theta\)だけずらしたものの集まりになる。すなわち1つの軌道を回転したものの集まりになる。それはハミルトニアン\(H\)に\(\theta\)が含まれないからである。
再び2次元自由粒子
2次元自由粒子のハミルトンヤコビの方程式の円対称な解を紹介しよう。解は式(\ref{kai161})で\(V=0\) とした \[ S=-E\;t+\alpha_\theta \theta\pm \int^r \sqrt{2m\left( E-\frac{\alpha_\theta^2}{2mr'^2}\right)} \;dr' \] である。これは最初に紹介した解(\ref{2ji})とは異なる。これを積分すると(過程は省略するが) \[ S=-Et+\alpha_\theta\theta\pm\alpha_\theta(\tan\phi-\phi) \] となる。ここで\(\phi\)は \( r\cos\phi=\alpha_\theta/\sqrt{2mE} \)を満たすものである。ここで\(\pm\)の\(+\)を選択すると、等高線と軌道は図6-7のようになるであろう。
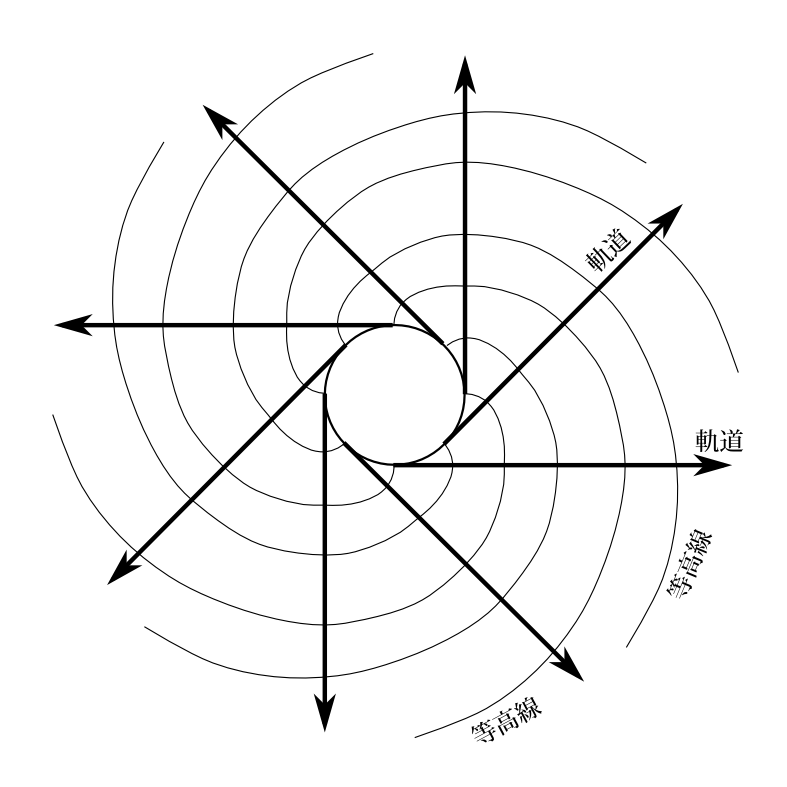
図6-7 2次元自由粒子の円対称な解の等高線と軌道。
角運動量の量子化
ここで量子力学との関係を少し述べたい。もしシュレディンガーの波動関数が \begin{equation} \psi\cong\exp\left(i\frac{S}{\hbar}\right) \label{sou31} \end{equation} と近似してよいなら、\(\theta\)が一回転したとき\(\psi\)の値は同じにならなければならない。だから\(\theta\)が\(2\pi\)増えたとき\(S/\hbar\)はちょうど\(2\pi\)の整数倍だけ変化しなければならない。すなわち\(n\)を整数として \[ \frac{\alpha_\theta\cdot 2\pi}{\hbar}=2\pi n \] でなければならない。式(\ref{tyu1})より \[ p_\theta=\alpha_\theta \] なので、 \begin{equation} p_\theta=n\hbar \label{sou32} \end{equation} という条件が出る。第4章式(14)で見たように、\(p_\theta\)というのは角運動量なので、これは量子力学でよく知られた角運動量の量子化である。 ただ式(\ref{sou31})というのは近似なので、式(\ref{sou32})という量子力学と同じ式が導出されたのは、何か意味があるのではなく、単なる偶然なのかもしれない。
6-10節 \(S\)が不変量であること
ハミルトンヤコビの方程式というのは一見すると各座標で異なる方程式のように見える。例えば2次元自由粒子の場合、直交座標では \[ \frac{1}{2m}\left[\left(\frac{\partial\, S}{\partial\, x}\right)^2+\left(\frac{\partial\, S}{\partial\, y}\right)^2\right]+\frac{\partial\, S}{\partial\, t} =0 \] であり、平面極座標では \[ \frac{1}{2m}\left[\left(\frac{\partial\, S}{\partial\, r}\right)^2+\frac{1}{r^2}\left(\frac{\partial\, S}{\partial\, \theta}\right)^2\right]+\frac{\partial\, S}{\partial\, t} =0 \] である。しかし実際この2つの偏微分方程式の解は共通である。一方の方程式の解は必ずもう一方の方程式の解になる。それを証明しよう。
\(q\)系のハミルトニアンは関数として、すなわち\(q,p,t\)からある数を与える規則として \[H=h(q_i,p_i,t) \] であるとしよう。すると ハミルトンヤコビの方程式は \[ h\left( q_i,\frac{\partial\, S}{\partial\, q_i},t \right)+\frac{\partial\, S}{\partial\, t}=0 \] となる。偏微分\(\partial\,/\partial\, q\)を\(q'\)の偏微分に書き改めると \begin{equation} h\left( q_i,\sum_k \frac{\partial\, q'_k}{\partial\, q_i}\frac{\partial\, S}{\partial\, q'_k},t \right)+\frac{\partial\, S}{\partial\, t}=0 \label{ky4} \end{equation} となる。次に\(q'\)系のハミルトンヤコビの方程式を作ろう。\(p\)と\(p'\)、\(H\)と\(H'\)の関係は定理4-3で示したように \[ p_i=\sum_k\frac{\partial\, q'_k}{\partial\, q_i}p'_k \] であり、座標変換に時間を含まないときは 定理4-4で示したように \[ H=H' \] であった。だから\(q'\)系のハミルトニアンは \[ H'=h\left(q_i(q'_k), \sum_k\frac{\partial\, q'_k}{\partial\, q_i}p'_k,t\right) \] である。そして ハミルトンヤコビの方程式は \[ h\left( q_i(q'_k),\sum_k\frac{\partial\, q'_k}{\partial\, q_i}\frac{\partial\, S}{\partial\, q'_k},t \right)+\frac{\partial\, S}{\partial\, t}=0 \] である。これは式(\ref{ky4})と同じ方程式である。よって2つの座標系のハミルトンヤコビの方程式の解は共通なのである。
定理6-3 座標の変換に時間を含まないときハミルトンヤコビの方程式の解は同じである。すなわち\(S\)は不変量である。
要するにある座標系のハミルトンヤコビの方程式を偏微分方程式の変数変換をして(例えばシュレディンガー方程式でも直交座標を極座標に変数変換するであろう。それと同じことをするということ)別の座標系で表すと、それはその座標系でのハミルトニアンから作られたハミルトンヤコビの方程式と一致するというわけである。以下の具体例を見ればよくわかると思う。
例6-1
2次元自由粒子の直交座標でのハミルトンヤコビの方程式は \[ \frac{1}{2m}\left[\left(\frac{\partial\, S}{\partial\, x}\right)^2+\left(\frac{\partial\, S}{\partial\, y}\right)^2\right]+ \frac{\partial\, S}{\partial\, t}=0\] である。この偏微分方程式を平面極座標に変数変換すると \[ \frac{1}{2m}\left[\left(\frac{\partial\, r}{\partial\, x}\frac{\partial\, S}{\partial\, r}+\frac{\partial\, \theta}{\partial\, x}\frac{\partial\, S}{\partial\, \theta}\right)^2+\left(\frac{\partial\, r}{\partial\, y}\frac{\partial\, S}{\partial\, r}+\frac{\partial\, \theta}{\partial\, y}\frac{\partial\, S}{\partial\, \theta}\right)^2\right]+ \frac{\partial\, S}{\partial\, t}=0 \] である。これに \[ \frac{\partial\, r}{\partial\, x}=\cos\theta \quad\quad \frac{\partial\, \theta}{\partial\, x}=-\frac{\sin\theta}{r} \quad\quad \frac{\partial\, r}{\partial\, y}=\sin\theta \quad\quad \frac{\partial\, \theta}{\partial\, y}=\frac{\cos\theta}{r} \] を代入すると \[ \frac{1}{2m}\left[\left(\frac{\partial\, S}{\partial\, r}\right)^2+\frac{1}{r^2}\left(\frac{\partial\, S}{\partial\, \theta}\right)^2\right]+ \frac{\partial\, S}{\partial\, t}=0 \] となる。一方平面極座標の自由粒子のハミルトニアンは \[ H=\frac{1}{2m}\left(p_r^2+\frac{p_\theta^2}{r^2}\right) \] であり、ハミルトンヤコビの方程式は \begin{equation} \frac{1}{2m}\left[\left(\frac{\partial\, S}{\partial\, r}\right)^2+\frac{1}{r^2}\left(\frac{\partial\, S}{\partial\, \theta}\right)^2\right]+ \frac{\partial\, S}{\partial\, t}=0 \label{tg1} \end{equation} である。だから2つの偏微分方程式は一致するのである。6-6節で求めた \[ S=-\frac{1}{2m}(\alpha_x^2+\alpha_y^2)t+\alpha_xx+\alpha_yy \] が両者に共通な解である (注 6-9節で紹介した \[ S=-Et+\alpha_\theta\theta\pm\alpha_\theta(\tan\phi-\phi) \] も両者に共通な解である。 ) 。 このSが平面極座標のハミルトンヤコビの方程式の解になっていることを代入して確かめてみよう。 Sに\(x=r\cos\theta,y=r\sin\theta\)を代入した \begin{equation} S=-\frac{1}{2m}(\alpha_x^2+\alpha_y^2)t+\alpha_xr\cos\theta+\alpha_yr\sin\theta \label{dais} \end{equation} を偏微分方程式(\ref{tg1})の左辺に代入すると \[ \frac{1}{2m}\left[ (\alpha_x\cos\theta+\alpha_y\sin\theta)^2+\frac{1}{r^2}(-\alpha_xr\sin\theta+\alpha_yr\cos\theta)^2 \right] -\frac{1}{2m}(\alpha_x^2+\alpha_y^2) \] となり、これは\(0\)となることが容易に確かめられる。【例終】
6-11節 解軌道も同じであること
2つの座標系でのハミルトンヤコビの方程式の解が共通なのはわかったが、それから \begin{equation} \frac{\partial\, S}{\partial\, \alpha_i}=\beta_i \qquad\qquad \frac{\partial\, S}{\partial\, q_i}=p_i \label{okoru} \end{equation} によって得られる解軌道は同じなのだろうか。 当然一致すると考えられる が、それを証明しよう。
\(q\)系と\(q'\)系の変換は時間を含まないとする。 \(q\)系のハミルトンヤコビの方程式の解を \[ S=Y(q_i,\alpha_i,t) \] とする。\(Y(q_i,\alpha_i,t)\)は不変量表示でなく関数形での表示とする。すると、今証明した定理6-3より、\(q'\)系でのハミルトンヤコビの方程式の解は \[ S=Y(q_i(q'_k),\alpha_i,t) \] となる。\(q_i\)についての\(q\)系の解軌道を求める式は \begin{equation} \frac{\partial\, Y(q_i,\alpha_i,t)}{\partial\, \alpha_i}=\beta_i \label{hak1} \end{equation} である。\(q'_i\)についての\(q'\)系の解軌道を求める式は \begin{equation} \frac{\partial\, Y(q_i(q'_k),\alpha_i,t)}{\partial\, \alpha_i}=\beta_i \label{hak2} \end{equation} である。\(\alpha_i,\beta_i,t\)から\(q'_k\)への写像は、式(\ref{hak1})の陰関数から求まった\(\alpha_i,\beta_i,t\)から\(q_i\)への写像に、さらに\(q_i\)から\(q'_k\)への座標変換での写像をしたものになる。すなわち\(q\)については\(q\)系の解軌道は\(q'\)系の解軌道に一致する。
\(p_i\)についての\(q\)系の解軌道を求める式は \begin{equation} \frac{\partial\, Y(q_i,\alpha_i,t)}{\partial\, q_i}=p_i \label{hak3} \end{equation} である。この\(q_i\)のところには式(\ref{hak1})で求まった\(q_i\)を入れるわけである。そうすれば \(\alpha_i,\beta_i,t\)の関数として\(p_i\)が求まる。 \(p'_i\)についての\(q'\)系の解軌道を求める式は \begin{equation} \frac{\partial\, Y(q_i(q'_k),\alpha_i,t)}{\partial\, q'_k}=p'_k \label{hak4} \end{equation} である。この\(q'_i\)のところには式(\ref{hak2})で求まった\(q'_i\)を入れるわけである。そうすれば \(\alpha_i,\beta_i,t\)の関数として\(p'_k\)が求まる。 式(\ref{hak4})は \[ \sum_i\frac{\partial\, q_i}{\partial\, q'_k}\frac{\partial\, Y(q_i(q'_k),\alpha_i,t)}{\partial\, q_i}=p'_k \] と変形できる。だから式(\ref{hak3})を使うとこれは \[ \sum_i\frac{\partial\, q_i}{\partial\, q'_k}p_i=p'_k \] となる。これは定理4-3で示した運動量の変換式と同一である。 だから\(\alpha_i,\beta_i,t\)から\(p'_k\)への写像は、\(\alpha_i,\beta_i,t\)から\(p_i\)への写像して、さらに\(p_i\)から\(p'_k\)への運動量の変換式に従った写像を続けたものになる。すなわち\(p\)についても\(q\)系の解軌道は\(q'\)系の解軌道と一致する。 解軌道が一致するのはハミルトンヤコビの方程式の解が同じときであり、それは座標変換に時間を含まないときである。だから今は
定理6-4 2つの座標系が時間を含まない座標変換で結ばれているとき、それぞれのハミルトンヤコビの方程式から導かれる解軌道は等しい。
ということを証明したわけである。
今の証明は少しピンとこないところがあったかもしれない。例6-2を見てもらえば、当たり前のことを言っているということがわかると思う。 要するに\[ \frac{\partial\, S}{\partial\, \alpha_i}=\beta_i \]は両座標系で共通であり、 \[ \frac{\partial\, S}{\partial\, q_i}=p_i \] は左辺右辺ともに共変ベクトルとして変換するということである。
例6-2
例6-1で述べた、2次元自由粒子のハミルトンヤコビの方程式の解の極座標表示(\ref{dais})の \[ S=-\frac{1}{2m}(\alpha_x^2+\alpha_y^2)t+\alpha_xr\cos\theta+\alpha_yr\sin\theta \] から解軌道を求めよう。 解軌道を求める式\(\partial\, S/\partial\, \alpha_x=\beta_x,\,\partial\, S/\partial\, \alpha_y=\beta_y\)は \[ -\frac{\alpha_x}{m}t+r\cos\theta=\beta_x \qquad\qquad -\frac{\alpha_y}{m}t+r\sin\theta=\beta_y \] となる。これは \[ r\cos\theta=\frac{\alpha_x}{m}t+\beta_x \qquad\qquad r\sin\theta=\frac{\alpha_y}{m}t+\beta_y \] となる。\(r\cos\theta=x,\;r\sin\theta=y\)と変換されるので、これは6-6節で求めた \[ x=\frac{\alpha_x}{m}t+\beta_x \qquad\qquad y=\frac{\alpha_y}{m}t+\beta_y \] と同じである。又もう一つの 解軌道を求める式\(\partial\, S/\partial\, r=p_r,\,\partial\, S/\partial\, \theta=p_\theta\)は \begin{equation} \alpha_x\cos\theta+\alpha_y\sin\theta=p_r \qquad\qquad -\alpha_x r\sin\theta+\alpha_yr\cos\theta=p_\theta \label{de1} \end{equation} となる。 一方定理4-3より運動量は \begin{eqnarray} p_r&=&\frac{\partial\, x}{\partial\, r}\;p_x+\frac{\partial\, y}{\partial\, r}\;p_y\notag\\ &=&\cos\theta\; p_x+\sin\theta \;p_y\notag\\ \notag\\ p_\theta&=&\frac{\partial\, x}{\partial\, \theta}\;p_x+\frac{\partial\, y}{\partial\, \theta}\;p_y\notag\\ &=&-r\sin\theta \;p_x+r\cos\theta \;p_y\notag \end{eqnarray} と変換するのであった。6-6節で述べたように\(p_x=\alpha_x,\,p_y=\alpha_y\)であった。だから式(\ref{de1})は 運動量の変換と一致しており、同じ運動量軌道を意味する。【例終】
6-12節 等高線と軌道が直交すること
中心力場のとき、極座標でのハミルトンヤコビの方程式の解\(S\)と、それに含まれる軌道は図6-6のように直交するとしていたが、証明はしていなかった。このことは\(S\)が不変量で解軌道が同じであることからただちにわかる。というのは、ある座標での解\(S\)とそれから導かれる解軌道は直交座標での解と解軌道でもあり、直交座標での\(S\)と軌道は直交するからである。 すなわち
定理6-5 1粒子の系で、直交座標でない座標系でハミルトンヤコビの方程式の解\(S\)を求め、その\(S\)から軌道を求めたとしよう。その座標系は直交座標との座標変換では時間を含まないとする。その\(S\)の等高線と軌道は、それを直交座標で描くと、直交する。
といえる。
6-13節 \(S\)とラグラジアンの関係
ハミルトンヤコビの方程式の解\(S\)とラグランジアン\(L\)の関係を述べよう。\(q_i(t)\)をハミルトンヤコビの方程式の解\(S\)から導かれる力学の法則を満たす軌道としよう。その軌道にそって\(S\)を時間微分すると \[ \frac{dS}{dt}=\sum_i\frac{\partial\, S}{\partial\, q_i}\dot{q}_i+\frac{\partial\, S}{\partial\, t} \] となる。 \[ \frac{\partial\, S}{\partial\, q_i}=p_i\qquad\qquad \frac{\partial\, S}{\partial\, t}=-H \] なので \[ \frac{dS}{dt}=\sum_i p_i\dot{q}_i-H \] である。ハミルトニアンの定義式 \[ H=\sum_i p_i\dot{q}_i-L \] を使うと、これは系のラグランジアン\(L\)に等しい。だから
定理6-6 力学の法則を満たす軌道にそって、その軌道に対応するハミルトンヤコビの方程式の解を時間で全微分したものは、ラグランジアンに等しい。すなわち \begin{equation} \frac{d S(q,t)}{dt}=L(q,\dot{q},t) \label{kai221} \end{equation}
といえるわけである (注 第5章を読んだ読者向けに言うと、 ハミルトンヤコビの解というのは母関数であった。すなわち、ハミルトンヤコビの方程式の解というのは \[ \sum_ip_i\dot{q}_i-H=\frac{dS}{dt} \] という式を満たすのであった。これが式(\ref{kai221})のわけである。 )。 これをある軌道\(q(t)\)で\(t_a\)から\(t_b\)まで積分すると \[ \int_{t_a}^{t_b}L dt=S[q(t_b),t_b]-S[q(t_a),t_a] \] となる。又、\(H\)に時間を含まないときは\(S=-Et+W(q)\)と置けるので \[ \int_{t_a}^{t_b}L dt=-E(t_b-t_a)+W[q(t_b)]-W[q(t_a)] \] が成り立つ。
例6-3
1次元自由粒子で式(\ref{kai221}) が成り立っていることを確かめてみよう。この場合のハミルトンヤコビの方程式の解\(S\)は、式(\ref{kai4})より \[ S=-\frac{p^2}{2m}t+p x \] である。\(p\)は定数である。そして \[ \frac{dS}{dt}=-\frac{p^2}{2m}+p\dot{x} \] である。\(p=m\dot{x}\)なので \[ \frac{dS}{dt}=\frac{1}{2}m\dot{x}^2 \] となる。これはラグランジアン \[ L=\frac{1}{2}m\dot{x}^2 \] に等しい。【例終】
6-14節 波動関数の位相とハミルトンヤコビの方程式の解と波動関数の位相
近似の条件
今まで、ある条件を満たせば、ハミルトンヤコビの方程式の解\(S\)を使って、シュレディンガー方程式の解\(\psi\)は \[ \psi\cong\exp\left(i\frac{S}{\hbar}\right)\] と近似できると述べてきた。その条件をここで考えよう。 簡単のため1粒子とするが何粒子でも考え方は同じである。波動関数を \[ \psi=\exp\left(i\frac{S}{\hbar}\right) \] とおいて、1粒子のシュレディンガー方程式 \[ -\frac{\hbar^2}{2m}\triangle \psi +V\psi=i\hbar \frac{\partial\, \psi}{\partial\, t} \] に代入してみよう。すると \begin{equation} \frac{1}{2m} \left[ \left|\nabla S\right|^2 -i\hbar \triangle S \right] +V=-\frac{\partial\, S}{\partial\, t} \label{ry0} \end{equation} となる。 Sの空間部分の変化は\(|\nabla S|^2\)と\(i\hbar \triangle S\)によって決定される。 もし \begin{equation} |\nabla S|^2\gg |\hbar\triangle S| \label{ry1-1} \end{equation} ならば、\(i\hbar\triangle S\)は 無視してよいということである。すると式(\ref{ry0})は \[ \frac{1}{2m} \left[ \left(\frac{\partial\, S}{\partial\, x}\right)^2+\left(\frac{\partial\, S}{\partial\, y}\right)^2+\left(\frac{\partial\, S}{\partial\, z}\right)^2 \right] +V+\frac{\partial\, S}{\partial\, t}=0 \] となり、ハミルトンヤコビの方程式と一致する。
自由粒子
具体的な例で見てみよう。まず自由粒子の場合を考えよう。この場合\(S\)は式(\ref{2ji})より \[ S=-Et+p_xx+p_yy+p_zz \] なので、\(S\)の2階微分は0である。だから、\(\exp\left(i\frac{S}{\hbar}\right)\)すなわち \[ \exp\left[\frac{i}{\hbar}(-Et+p_xx+p_yy+p_zz)\right] \] はシュレディンガー方程式の解になる。
ポテンシャルのある場合
次に\(x,y\)座標で、ポテンシャルは\(y\)方向のみに依存する場合を考える。具体的には一様重力場と思ってもらえればよい。この場合のハミルトンヤコビの方程式の解は、 \[ S=-Et+p_xx+\int^y\sqrt{2m\left(E-\frac{p_x^2}{2m}-V(y')\right)}dy' \] である(これが解であることは入れてみればすぐわかる。式(\ref{koremo})参照)。これは\(y\)方向の運動量が正の場合である。条件式(\ref{ry1-1})を今の場合に適用しよう。 \[ \frac{\partial\,^2 S}{\partial\, x^2}+\frac{\partial\,^2 S}{\partial\, y^2} =-m\frac{dV}{dy}\frac{1}{\sqrt{2m\left(E-\frac{p_x^2}{2m}-V(y)\right)}} \] であり、\(-\frac{dV}{dy}\)は\(y\)方向の力なので\(F_y\)と書き、\(\sqrt{2m\left(E-\frac{p_x^2}{2m}-V(y)\right)}=p_y\)なので \[ \hbar\left( \frac{\partial\,^2 S}{\partial\, x^2}+\frac{\partial\,^2 S}{\partial\, x^2}\right) =\hbar \frac{F_y}{v_y} \] である。一方 \[ \left(\frac{\partial\, S}{\partial\, x}\right)^2+\left(\frac{\partial\, S}{\partial\, y}\right)^2 = p_x^2+p_y^2 \] である。だから \begin{equation} \frac{\left|\hbar \frac{F_y}{v_y}\right|}{p_x^2+p_y^2}\ll 1 \label{ry2c} \end{equation} なら条件式(\ref{ry1-1})が満たされることになり、ハミルトンヤコビの方程式の解\(S\)を \(\exp\left(i\frac{S}{\hbar}\right)\)としたものはシュレディンガー方程式の解に近いといえる。式(\ref{ry2c})をながめれば、運動量が大きく、力が弱ければこの近似は成り立つということがわかる。\(\hbar=10^{-34}\)J・s程度なので、\(m,F\)が1kg,1N程度なら成り立つわけである。又、\(|F_y/v_y|\)という項があるので、力の方向の速さが小さいときは、例え力に直角の向きの運動量が大きくてもこの近似は使えない。
一様重力場

図6-8 自由落下の粒子では\(\psi\cong\exp\left(i\frac{S}{\hbar}\right)\)という近似は粒子が最上点にいる場合は使えない。最上点より上は\(S\)の定義外である。
さて、一様重力場で図6-8のような上昇して下降する運動に対応する波動関数の様子をハミルトンヤコビの方程式の解\(S\)を使って想像してみよう。この場合、力\(F_y\)は一定なので粒子が下の方にあり、そのために運動量が大きければ条件(\ref{ry2c})は満たされる。しかし最上点付近では\(v_y\to 0\)となるので条件(\ref{ry2c})は満たされなくなる。そして最上点より上では\(S\)が定義されていないので、ここはシュレディンガー方程式から求めるしかない。粒子が上昇するときは、式(\ref{koremo})より、 \[ S_{(-)}=-Et+p_xx-\int^y\sqrt{2m\left(E-\frac{p_x^2}{2m}+mgy'\right)}dy' \] であり、下降するときは \[ S_{(+)}=-Et+p_xx+\int^y\sqrt{2m\left(E-\frac{p_x^2}{2m}+mgy'\right)}dy' \] である。これを重ね合わせた \[ A\exp\left(i\frac{S_{(-)}}{\hbar}\right)+B\exp\left(i\frac{S_{(+)}}{\hbar}\right) \] というのが最上点より少し下でのシュレディンガー方程式の解に近いであろう。
6-15節 まとめ
ハミルトンヤコビの方程式の解から正準方程式という微分方程式の解が得られるわけだが、実際の微分方程式を解く手法としてのこの方法は何のメリットもない。そうではなく、その逆にメリットが有る。すなわち古典力学の軌道からハミルトンヤコビの方程式の解の概要が得られるということである。その方法とは
1. 1つの古典軌道を力と直角の方に平行移動して軌道群を作る(仮説6-1)。
2. その軌道群に直角な線を引く(定理6-5)。これがW一定の線である。
3. W一定の線の間隔は\(p\)に逆比例するということを使って、又は等高線群は力に直角の方向に平行移動したものであるという性質を使って、等高線群を引く。
正準方程式の解からハミルトンヤコビの方程式の解が得られるということは証明はしていないし、私自身調べてもいないが、おそらく得られると思う (注 2022年10月追記:ハミルトンヤコビの方程式の解は正準方程式から得られる。私はそのことをスミルノフ高等数学教程9巻で学んだ。) 。 ハミルトンヤコビの方程式の解は、ある条件下では量子力学の波動関数の位相に近似できる。 だから上記1,2,3の方法によって古典軌道から波動関数の概要が得られるということである(例えば節6-7の一様重力場)。我々は多くの経験から古典軌道というものの予想がつく。しかしシュレディンガー方程式の解の概略は予想がつかない。しかしながら、ハミルトンヤコビの方程式の解がそれを結びつけてくれるわけである。 ここにハミルトンヤコビの方程式の最大のメリットが有る。
この章の説明は具体例から一般論へと言う説明をとったのでややまとまりが欠けたと思っている。