第1章 量子力学の原理
この章では量子力学の基本原理を述べる。通常の量子力学の体系とは異なる記述の仕方をしているが、私が量子力学を解釈して、これがその意味しているところだろうと思うところを書いた。確率振幅というのは計算のための便宜であり、確率分布こそが物理的意味のあるものだということを強調した。確率分布というものの存在自体にも大いに疑問を感じるが、そこで止まっていても先に進まないので、とりあえず量子力学の体系というものを述べた。
1.1節 基本原理
量子力学の原理を古典力学と対比して述べたい。今、一つの粒子がポテンシャル中を運動しているとする。説明をわかりやすくするため、スピンは無視する。古典力学では、最初の位置と運動量が与えられれば、その後の運動は完全に決まる。量子力学では最初の位置の確率分布と運動量の確率分布が与えられれば、その後の位置の確率分布と運動量の確率分布が完全に決まる。位置の確率分布とは、簡単に言えば、実際に位置を測ってある位置で粒子を見出す確率のことである。運動量の確率分布についても同様。量子力学ではあるゆる瞬間で、位置や運動量、エネルギーなどの物理量の確率分布を持っている。私の目の前に鉛筆があり、その中には電子がある。その電子が今どのような確率分布の状態にあるかを私は知らない。しかし私が知っていようが知るまいがこの電子には確率分布が付随しているということである。そして測定したら、その測定値を見出す確率がその確率分布に従うということである。ここらへんには疑問を感じるが、量子力学の体系ではそういうことになっている。
古典力学では位置と運動量が定まれば、他の物理量は定まる。単に位置と運動量の関数だからである。一方、量子力学では位置の確率分布と運動量の確率分布が定まれば他の物理量の確率分布も定まる。 その結果として、位置の確率分布と運動量の確率分布が与えられれば、その後の他の物理量の確率分布の時間発展も一意的に決まる。 古典力学では系の状態という言葉はあまり使わないが、量子力学では常に登場する。量子力学で使う「系の状態」というのも、普通の意味と同じであり、文脈によって意味も異なったりするが、ここでは 「ある状態Aとある状態Bは同じ状態だ」といえば、それは位置や運動量などすべての物理量の確率分布がAとBで等しい場合であるとする。位置の確率分布と運動量の確率分布で他の物理量の確率分布も定まるので、系の状態は位置の確率分布と運動量の確率分布で定まると言える。
測定のときは、確率分布の時間発展は一意的には決まらない。例えば位置を測るとする。どこで粒子を見出すことができるかは、確率的にしかわからない。そして、あるAというところで検出したとしよう。すると位置の確率分布は、Aだけが0でない確率分布に瞬間的に移る。というのはもし、Aで検出された直後に再び位置を測れば、当然100%の確率でAで検出されるはずだからである。これは測定後にはAだけが0でない確率分布にあるという意味に他ならない。位置の確率分布の突然の変化に伴い、運動量の確率分布も変化する。どう変化するかはおいおい述べていくが、運動量はどの値も等しい確率分布になる。他の物理量を測っても、測定値だけが0でない確率分布に移り、その他の物理量の確率分布もそれに応じて変化する。測定値だけが0でない確率分布となる状態のことを測定状態と呼ぶことにする。エネルギーを測って測定値が100ジュールだったら、状態はエネルギー100ジュールの測定状態に飛び移るし、この粒子は今、エネルギーが100ジュールの測定状態にあるといえば、エネルギーを測れば必ずエネルギーは100ジュールになる。
古典力学では測定値は連続であるが、量子力学では測定値は必ずしも連続ではない。角運動量の測定値は常に飛び飛びであるし、束縛状態のエネルギーも飛び飛びの測定値しか現れない。以上まとめると
【原理1】あらゆる瞬間で、物理量の、どの測定値が得られるかについ
ての確率分布が存在する。
【原理2】位置の確率分布と運動量の確率分布で他の物理量の確率分布
も定まる。
【原理3】確率分布の時間発展は、測定時を除いて、現在の確率分布か
ら一意的に決まる。
【原理4】測定すると、その物理量の確率分布は、測定値だけが0でな
い確率分布に瞬間的に移る。この状態を測定状態という。
【原理5】測定値は必ずしも連続ではない。
量子力学の体系自体は難しくない。各物理量に対して確率分布が存在し、それが一意的に時間発展する。現在が未来を決める。その時間発展方程式は書き下すことができない程ややこしい。しかしながらややこしいと言っても、古典力学でも現実の系を扱うのは、静的であれ動的であれ、きわめて煩雑なのであり、教科書に出てくるものは、理想化した例なのである。あと知らなければならないことは
1. 確率分布の時間発展は一意的といっても具体的にはどんな方程式
なのか。
2. 位置と運動量の確率分布で他の物理量の確率分布も決まるとい
うが、具体的にはどういう関係にあるのか。又、位置と運動量の
確率分布には関係はあるのか。
3. 測定時には、その物理量は測定値のみ0でない確率分布に移ると
して、他の物理量はどのような確率分布に移るか。
4. 測定値は飛び飛びの値のときもあるというが、どんな値が現れる
のか。
である。これらのことを、実験的にしろ、合理的推論にしろ、見出すことである。
尚、ここで述べた原理は電子などの物質粒子を想定して述べている。私は量子電磁気学の知識がないので、なんとも言えないが、量子電磁気学などでは「位置と運動量の確率分布で状態が決まる」というのは当てはまらないのかもしれない。素粒子論などは全く知識がないのでなんとも言えない。量子電磁気学は私も勉強してみたことはあるのだが、何か、物理的意味のわからない計算ばかりで、これをいくら学んでも自然現象を理解することはできないと思いやめてしまった。
測定の結果が確率でしかわからないと考えるのは、粒子が波動として行動し粒子として検出されるからである。物質を結晶にぶつけて散乱させると干渉模様が見られる。物質は波動として行動するのである。一方精密に実験すれば物質は1つ1つの塊として検出される。ミリカンの電子の電荷の測定などもその一例だろう。干渉模様も弱い波動で実験すれば、粒子がポツンポツンと来る。
測定をすると確定値をとるとして話をしてきたが、実際は測定値には幅がある。となると例えば位置の\(x\)座標を測定してある点から10nm~20nmの範囲にあるという結果を得たら、位置の確率分布はその範囲は0でなく、
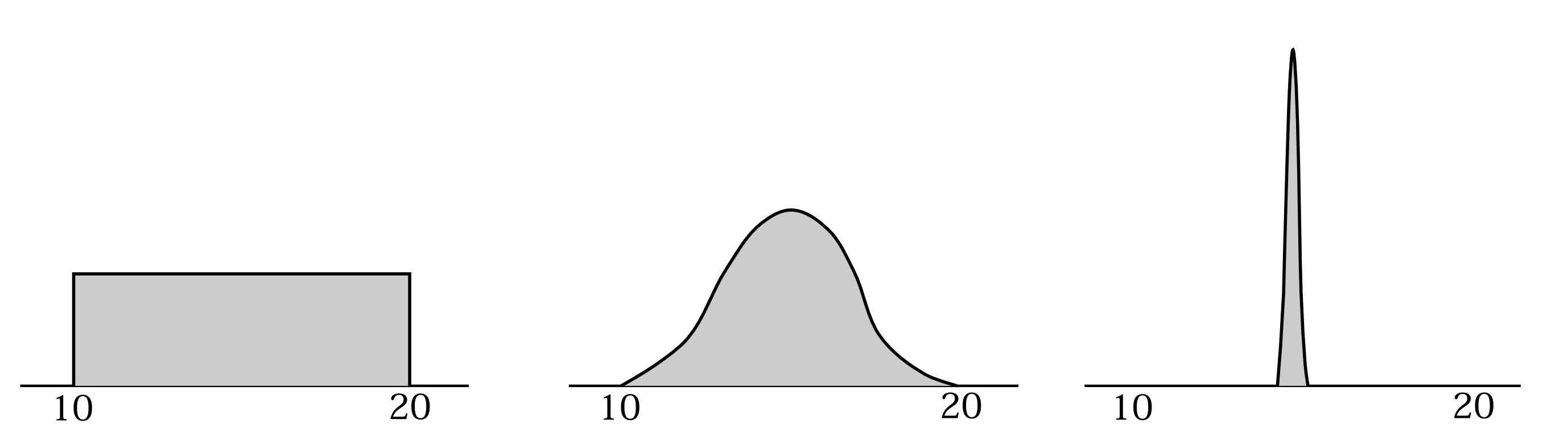
図1.1 10nm~20nmの範囲で粒子を検出した
その範囲外は0という状態に飛び移るだろう。 直後の確率分布の想像図
しかし10nm~20nmの間でも確率分布が図1.1の左図のようになるか、真ん中の図のようになるか、又は右図のようになるのかは、これだけの測定結果だけでは何も言えない。量子力学はそのことについて何も述べていないのである。
さて確率分布は時間発展方程式に従うが、測定のときは従わないと述べた。しかし、測定という行為も自然現象の1つである。それなのになぜ、測定のときもその時間方程式に従わないのか。これはどう考えても筋が通っていないのである。この問題を観測問題という。ファインマンの本などでは、別に矛盾はないような書き方をしているが、それは、あまり考えてないか、知的誠実さに欠けているのである。観測問題については一応第8章で考察しているが、結局はわからないことである。
1.2節 確率振幅、変換行列の導入
今から確率振幅という、物理的意味のわかりづらいものを導入する。確率分布のままで扱うと、時間発展方程式が煩雑になり、又、物理量間の確率分布の関係が煩雑になる。そのための計算の便宜として確率振幅というものを導入する。我々は任意の物理量での確率振幅を見出したいのだが、
【確率振幅の定義】 ある物理量の確率振幅とは、その絶対値の2乗がその物理量の確率分布に等しく、他の物理量の確率振幅とはユニタリー変換で結ばれるもの
である。そういうものを導入したいのである。
簡単のため1粒子の系を考え、スピンは無視しよう。状態を指標\(\lambda\)で区別する。まず、位置と運動量の確率振幅を導入しよう。任意の状態\(\lambda\)での位置の確率分布\(P(x,y,z;\lambda)\)と運動量の確率分布\(P(p_x,p_y,p_z;\lambda)\)に対して (注 \(P(x,y,z)\)と\(P(p_x,p_y,p_z)\)は同じ\(P\)を使っているが、異なる関数である。本来は\(P_x(x,y,z),P_p(p_x,p_y,p_z)\) などと区別すべきなのだが、それだと記号が煩雑になってしまうので同じ記号を使った。今後も誤解が生じないと思われるところでは、このように使われている変数で関数自体を区別することにする。) 、絶対値の2乗が確率分布に等しく、互いに線形変換で結ばれている確率振幅というものが存在する。正確に言うと \begin{equation} P(x,y,z;\lambda)=|\psi(x,y,z;\lambda)|^2\qquad P(p_x,p_y,p_z;\lambda)=|\varphi(p_x,p_y,p_z;\lambda)|^2 \label{jo1} \end{equation} \begin{equation} \psi(x,y,z;\lambda)=\sum_{p_x,p_y,p_z} U(x,p_x)U(y,p_y)U(z,p_z)\varphi(p_x,p_y,p_z;\lambda) \label{jo2} \end{equation} という関係を満たす状態\(\lambda\)ごとの関数\(\psi(x.y,z;\lambda),\;\varphi(p_x,p_y,p_z;\lambda)\)とユニタリー行列\(U(x,p_x)\)、\(U(y,p_y)\)、\(U(z,p_z)\)が――不思議なことに――存在する。ここで、\(\sum_{p_x,p_y,p_z}\)は\(p_x,p_y,p_z\)の取りうる値すべてで取るという意味。今後もそういう意味で使う。 この\(\psi(x.y,z;\lambda),\;\varphi(p_x,p_y,p_z;\lambda)\)は状態ごとに異なり、複素数である。\(U(x,p_x),\;U(y,p_y),\;U(z,p_z)\)は状態にはよらない。 この\(\psi(x,y,z;\lambda)\)を位置の確率振幅という。いわゆる波動関数というものである。\(\varphi(p_x,p_y,p_z;\lambda)\)を運動量の確率振幅という。\(U(x,p_x)\)は運動量\(p_x\)から位置\(x\)成分への変換行列という。 変換行列がユニタリーであることから、逆変換は \begin{equation} \varphi(p_x,p_y,p_z;\lambda)=\sum_{x,y,z} U^*(x,p_x)U^*(y,p_y)U^*(z,p_z)\psi(x,y,z;\lambda) \label{jo3} \end{equation} となる。 尚、第4章でも述べるが、規格化定数を除いて \[ U(x,p_x)=\exp(ip_x x/\hbar) \] である。ここで\(\hbar\)はプランク定数を\(2\pi\)で割ったもの。確率振幅自体は確率分布の平方根なので存在するに決まっているが、2つの確率振幅が線形変換で結ばれているのは実に不思議な話である。この2つの式を満たすものが存在するというのは、確率分布の性質であり、一種の自然法則である。 このように変換行列が存在することは、位置の確率分布と運動量の確率分布は両方が任意の確率分布をとることができるわけではなく、互いに関係を持つということを意味する。 そして変換行列が\(U(x,p_x)=\exp(ip_x x/\hbar)\)であることから、いわゆる不確定性原理が成り立つことになる。このことについては第9章で論じる。
(\ref{jo1}),(\ref{jo2})を満たす確率振幅と変換行列は無限にある。それは簡単に言えば、(\ref{jo1}),(\ref{jo2})を満たす確率振幅に絶対値1の複素数を掛けても(\ref{jo1})は満たされ、それに合わせて、変換行列も変えればいいからである。又、(\ref{jo1}),(\ref{jo2})を満たす確率振幅と変換行列の複素共役も(\ref{jo1}),(\ref{jo2})を満たすからである。詳しくは第2章で論じる。
尚、ここでは本来は連続量として扱わなければならない量を離散化して扱った。積分記号で表さなければいけないところを和で表した。測定変数は飛び飛びの時もあり、別々に扱うのが面倒なので、今後も原則、連続変数も離散化して扱うことにする。元々連続などというのは、空間や物体がいくらでも細かく分割できるという観察から――この観察自体が、せいぜい人間の目の見える範囲程度で行われたことだろうが、今はもちろん技術的に人間の目より細かく分割できるが――生じた空想である。離散化されたものの極限が連続なのだから、物理では何でも離散化すればいいのである。連続というのは一種の理想化である。
さて、今位置の確率振幅\(\psi(x,y,z)\)が与えられると\(|\psi(x,y,z)|^2\)によって位置の確率分布がわかることになる。又(\ref{jo3})よって運動量の確率振幅がわかり、運動量の確率分布もわかる。ということは位置の確率振幅が与えられれば、位置の確率分布と運動量の確率分布の両方がわかり、ということは状態がわかるということである。これは運動量の確率振幅でもいえることで、運動量の確率振幅が与えられれば状態は決まる。
1.3節 エネルギーの確率振幅
位置や運動量だけでなく、あらゆる物理量で、その絶対値の2乗が確率分布に等しく他の物理量の確率振幅とユニタリー変換で結ばれる確率振幅が存在するのだが、それは今求めた位置の確率振幅から必然的に――位相の任意性はあるが(第2章参照)――決まってしまう。
まずエネルギーの確率振幅について述べよう。 (\ref{jo1}),(\ref{jo2})を満たすあらゆる状態\(\lambda\)での位置の確率振幅があるわけだが、その状態\(\lambda\)が、エネルギーの値が\(\varepsilon\)の測定状態であるときの、位置の確率振幅を\(k(x,y,z;\varepsilon)\)だとしよう。同じエネルギー値の測定状態で2つ以上の独立な位置の確率振幅がある場合があるが――その場合、そのエネルギーは縮退しているという――記号が煩雑になるだけで何も本質的なことは変わらないので、縮退していないとする。 この\(k(x,y,z;\varepsilon)\)は不思議なことに必ずユニタリー行列となる。つまり \[ \sum_{x,y,z} k^*(x,y,z;\varepsilon)k(x,y,z;\varepsilon')=\delta_{\varepsilon\varepsilon'} \] である。 これも確率分布のもつ性質の1つであり、自然法則の1つである。この\(k(x,y,z;\varepsilon)\)と状態 \(\lambda\)での位置の確率分布\(\psi(x,y,z;\lambda)\)を使って任意の状態\(\lambda\)でのエネルギーの確率振幅を \begin{equation} \varphi(\varepsilon;\lambda)\equiv\sum_{x,y,z}k^*(x,y,z;\varepsilon)\psi(x,y,z;\lambda) \label{tua} \end{equation} と定義(注 位相の任意性があるので、これは無数にあるエネルギーの確率振幅のうちの一つである。第2章参照。)する。すると不思議にもエネルギーの確率振幅の絶対値の2乗はエネルギーの確率分布に等しくなる。式で書くと \[ P(\varepsilon;\lambda)=|\varphi(\varepsilon;\lambda)|^2 \] となる(注 尚、縮退している場合は、縮退しているものを合わせたものが確率分布に等しくなる。)。これも確率分布の持つ物理的性質についての量子力学の主張であり、数学的事実ではない。 尚、逆変換は \[ \psi(x,y,z;\lambda) =\sum_{\varepsilon}k(x,y,z;\varepsilon)\varphi(\varepsilon;\lambda) \] である。 エネルギーの確率振幅がこの関係で位置の確率振幅と関係づけられているということは、エネルギーの確率振幅が定まれば、位置の確率振幅が定まる。ということはエネルギーの確率振幅が与えられた場合でも状態は定まるということである。
定義の理由
エネルギーの確率振幅を(\ref{tua})のように定義した理由を述べよう。 変換行列の成分というものは、線形代数学でおなじみのことだが、変換される側の基底を変換後の基底で表したものである。 だから、エネルギーから位置への変換行列は、エネルギーの確率振幅の基底を位置の確率振幅で表したものとなる。 ところで、エネルギー\(\varepsilon\)の測定状態では、エネルギーの確率分布は\(\varepsilon\)のみ1で他では0なので、確率振幅の絶対値の2乗がその確率分布に等しくなるためには、確率振幅も\(\varepsilon\)のみ1で他では0とすれば良い。 ということはエネルギー測定状態がエネルギーの確率振幅の基底だということになる。 つまり、エネルギーから位置への変換行列は、エネルギーの測定状態を位置の確率振幅で表したものになる。 それゆえ、エネルギーから位置への変換行列は\(k(x,y,z;\varepsilon)\)となる。この逆行列でエネルギーの確率振幅を定義したのである。 このようにある必然性を持って定義したのだが、任意の状態で確率振幅の絶対値の2乗が確率分布と等しくなるという必然性はないわけで、もし本当に実験的にそれが成り立つなら、これは驚きであり、確率分布にそういう性質があるということである。
1.4節 角運動量の確率振幅
他の確率振幅もエネルギーのときと同様に定義する。しかし位置の一部としか変換しない物理量もある。それでそういう例として角運動量の\(z\)成分の確率振幅の導入の仕方を述べよう。状態\(\lambda\)での位置の確率振幅を極座標\(r,\theta,\phi\)で\(\psi(r,\theta,\phi;\lambda)\)と表そう。必ずしも極座標で表す必要はなく、要は\(\phi\)とその他の座標で表せばいいのだが、極座標が馴染み深いのでそうしただけである。 角運動量の\(z\)成分の値が\(l_z\)である測定状態を位置の確率振幅で表すと、 \(l_z\)に依存する\(\phi\)の関数\(k(\phi;l_z)\)と\(r\)と\(\theta\)の任意の関数\(f(r,\theta)\)との積となる。 つまり \[ k(\phi;l_z)\cdot f(r,\theta) \] となる。これも確率分布の性質を表す自然法則の一つである。これは\(\phi\)の部分以外は任意の関数で良いということである。 \(k(\phi;l_z)\)はエネルギーのときと同様にユニタリー行列となる。この\(k(\phi;l_z)\)と位置の確率振幅\(\psi(r,\theta,\phi;\lambda)\)を使って、任意の状態\(\lambda\)での角運動量の値が\(l_z\)の確率振幅を \[ \varphi(r,\theta,l_z;\lambda)\equiv \sum_{\phi}k^*(\phi;l_z)\psi(r,\theta,\phi;\lambda) \] と定義する。不思議なことにこの確率振幅の絶対値の2乗も――エネルギーのときと同様に――確率分布と等しくなる。つまり式で書くと \[ P(r,\theta,l_z;\lambda)=|\varphi(r,\theta,l_z;\lambda)|^2 \] となる。逆変換は \[ \psi(r,\theta,\phi;\lambda)= \sum_{l_z}k(\phi;l_z)\varphi(r,\theta,l_z;\lambda) \] となる。\(\phi\)以外は変換されないので、これらの式を簡略化して書くと \[ \varphi(l_z;\lambda)\equiv \sum_{\phi}k^*(\phi;l_z)\psi(\phi;\lambda) \qquad P(l_z;\lambda)=|\varphi(l_z;\lambda)|^2 \qquad \psi(\phi;\lambda)= \sum_{l_z}k(\phi;l_z)\varphi(l_z;\lambda) \] ということである。 他の物理量も同様に定義される。そうは言っても量子力学で頻繁に出てくる物理量はあとは角運動量の2乗くらいしかない。具体的な変換行列については第4章を見て欲しい。
#1.5節 確率振幅、変換行列一般のこと
基本的には、ある一つの物理量の確率振幅で状態は決まる。位置の確率振幅でも状態は決まるし運動量でも決まる。エネルギーでも決まるが、角運動量の確率振幅は位置座標の一部としか変換しないので系の状態は決まらない。しかし、その変数の部分の状態は決まる。状態を位置の確率振幅で表すとき位置表示といい、運動量の確率振幅で表せば運動量表示という。この言い方は線形代数学での使い方と同じである。
確率振幅と変換行列についてのいろいろな性質を述べてきたが、確率振幅が線形変換で結ばれるとか、その変換がユニタリーであるなどは、自然界に現れる確率分布の性質を述べているのであって、数学的な事実ではない。確率振幅の変換は線形変換なので、線形代数学の知識が大いに役立つ。数学の線形代数学と違うところは変換行列が積の形になっている場合があること、ベクトルの大きさが1のものに限定していること、それと、これは第2章で述べるが、同じ状態でもそれを表す確率振幅がいくつもあることなどである。確率振幅は数学でいうベクトル空間にはならないが、線形代数学での使える定理はたくさんある。
確率振幅の導入の仕方は少し分かりづらい説明になってしまった。1つには私の理解が浅いこともあるのだが、もう一つには、確率振幅、変換行列というものが物理的に極めて不自然だからであろう。任意の物理量\(B\)の状態\(\lambda\)の確率分布\(P(b;\lambda)\)に対し、確率振幅というものが存在するのだが、それは絶対値の2乗が\(P(b;\lambda)\)に等しく、他の物理量の確率振幅とユニタリー変換で結ばれる (注 補足しておくと、確率振幅の変換において、 測定変数は他のすべての測定変数と変換するわけではない。\(x\)は\(p_x\)とは変換するが、\(p_y\)とは変換しないし\(l_z\)とも変換しない。では、どういう変数どうしが変換するかと言うと、その答えは――本来は実験的に見いだされるべきなのだが――第4章で述べる固有ベクトル法にある。) ものである。そして変換行列と確率振幅は、位置と運動量の確率振幅をその確率分布から定めてしまえば、自動的に定まるわけである。だからこそ私は【原理2】のように、位置と運動量の確率分布が定まれば、他の物理量の確率分布も定まるであろうと考えたわけである。 では、 最初に位置とエネルギーの確率分布から確率振幅を決め、それから運動量などの確率振幅を決めていく方法は可能なのだろうか。これについては、そういうことができる系もあるが、できない系もあるというのが答えである。できない系というのは、位置とエネルギーの確率分布からだけでは状態が決まらない系――いわゆるエネルギーが縮退している系――である。状態が決まらないのに、その確率分布から、状態が決まってしまう確率振幅を定めることはできない。これは古典力学でも同じことであり、例えば自由粒子の系では、同じ運動エネルギーでも向きが異なる状態が無限にある。
いくつかの命題
ここでいくつかの命題を証明しておこう。
命題1.1 測定値\(a'\)の測定状態での物理量\(A\)の確率振幅\(k(a;a')\)は、測定値\(a'\)のみ1で他は0とすればよい。つまり \[ k(a;a')=\delta_{aa'} \] とすればよい。測定状態はその表示での基底となるということである。
これはエネルギーの確率振幅の定義の理由のところ(1.3節)で既に述べたが、改めて証明しておこう。
【証明】測定値が\(a'\)の測定状態での物理量\(A\)の確率分布\(P(a;a')\)は
\[P(a;a')=\delta_{aa'}\]
である。だから測定値が\(a'\)の測定状態の確率振幅は、その絶対値の2乗が確率分布に等しくなるためには、
\[k(a;a')=\alpha\cdot\delta_{aa'}\]
でなければならない。ここで\(\alpha\)は絶対値が1の任意の複素数である。2.1節で述べるが、確率振幅の位相は自由に変えることができるので
\(k(a;a')=\delta_{aa'}\)
とすることができる。【証明終】
命題1.2 物理量\(B\)から物理量\(A\)への変換行列\(U(a,b)\)は、測定値\(b\)の測定状態での物理量\(A\)の確率振幅\(k(a;b)\)に等しい。つまり \[ U(a,b)=k(a;b) \] である。 変換行列は、変換される側の測定状態を変換後の確率振幅で表したものということである。
これもエネルギーの確率振幅の定義の理由のところ(1.3節)で既に述べたが改めて証明する。
【証明】線形代数学でよく知られているように、変換行列\(U(a,b)\)は、変換される側である\(B\)の基底を、変換後の\(A\)の基底で表したものであるが、その物理量\(B\)の基底は、命題1.1より、その測定状態である。だから\(B\)の基底を\(A\)で表したものは、\(B\)の測定状態での\(A\)表示である\(k(a;b)\)である。【証明終】
命題1.3 物理量\(B\)から物理量\(A\)への変換行列\(U(a,b)\)の絶対値の2乗は、測定値\(b\)の測定状態での物理量\(A\)の確率分布\(P(a;b)\)に等しい。つまり \[ |U(a,b)|^2=P(a;b) \] である。 変換行列の絶対値の2乗は、変換される側の測定状態での変換後の物理量の確率分布ということである。
【証明】命題1.2より \(U(a,b)=k(a;b)\)であるが、これの絶対値の2乗をとり、\(|k(a;b)|^2=P(a;b)\)であることを考慮すればよい。【証明終】
命題1.4 物理量\(B\)の測定値\(b\)の測定状態にあるとき、物理量\(A\)を測り、測定値が\(a\)である確率\(P(a;b)\)はその逆の確率、すなわち、物理量\(A\)の測定値\(a\)の測定状態にあるとき、物理量\(B\)を測り、測定値が\(b\)である確率\(P(b;a)\)に等しい。 つまり \[ P(a;b)=P(b;a) \] である。
【証明】変換行列はユニタリ―なのだから \(U^*(a,b)=U(b,a)\) である。この絶対値の2乗を取れば\(|U(a,b)|^2=|U(b,a)|^2\)である。そして命題1.3より、\(|U(a,b)|^2=P(a;b)\)、\(|U(b,a)|^2=P(b;a)\)だからである。【証明終】
ユニタリー変換である必要はあるか
変換行列はユニタリーとなる必然性はあるのだろうか。これはないと思う。 線形代数学でよく知られているように、変換行列がユニタリーであることは、ベクトルの大きさが変換によって変わらないための必要十分条件である。今の場合、それぞれの物理量でのすべての測定値での確率の和(全事象)が変わらないということである。しかし全事象の確率は物理量ごとに異なっていても構わない。 例えばある状態で位置の確率振幅の絶対値の2乗の和が3で、それを変換行列でエネルギーの確率振幅に変換した結果、エネルギーでの和が10だったとしよう。 ある位置を取る確率と、あるエネルギーを取る確率とを、これでは比べられないではないかと思うかもしれないが、全事象の確率で割ればいいだけなのである。位置の確率は3で割り、エネルギーの確率は10で割ればいいだけなのである。 そうすれば比較に意味がある。だが自然はユニタリーを選んでいるということである。ユニタリー行列であることによる重要な帰結は、 命題1.4に記したように、測定状態\(a\)のときに測定値\(b\)を取る確率と、その逆の測定状態\(b\)のときに測定値\(a\)を取る確率が等しいことである。つまり \[ P(b;a)=P(a;b) \] となることである。
確率振幅の変換と単なる測定変数の変換を混同してはならない
尚、位置の確率振幅を 直交座標\(x,y,z\)を測定変数として\(\psi(x,y,z)\)と表していたものを、極座標で\(\psi(r,\theta,\phi)\)と表すのに変えることは確率振幅の変換ではない。単なる測定変数の名称の変更である。空間座標を回転させて新たな直交座標 \(x',y',z'\)で確率振幅を\(\psi(x',y',z')\)と表すのも確率振幅の変換ではない。これも単なる名称の変更である。運動量の確率振幅においても\(\varphi(p_x,p_y,p_z)\)と表していたものを、空間座標を回転させて新たな直行座標での運動量\(p'_x,p'_y,p'_z\)で\(\varphi(p'_x,p'_y,p'_z)\)と表しても、これは単なる名称の変更である。 2粒子系などで、それぞれの粒子の直交座標から相対座標、重心座標にして位置の確率振幅を表すのも、 直交座標から極座標へ移すのと同様、 名称の変更であり、確率振幅の変換ではない。
1.6節 2粒子以上の確率振幅
今まで1粒子の系を扱ってきたが、実際の世界は無数の粒子が相互作用し合っている。今まで確率分布\(P(x,y,z)\)などとしてきたが、これは正確ではない。実際は周りの粒子の変数も加えなければならないし、本当は全宇宙の粒子を加えなければならない。 \(P(x,y,z)\)として意味を成すのは周りの粒子の測定変数を暗黙のうちに指定しているか、相互作用がなくこの確率分布が他の粒子に影響を受けない場合である。多粒子系に話を拡張するのだが、粒子の種類はすべて異なる系に話を限定する。現実的にはそんなことはありえないが、同種粒子系だと少し話がややこしくなってしまうからである。
多粒子系への拡張は、今まで3次元で行ってきたことが単にそれ以上の次元になるというだけのことである。それゆえ、簡潔に式を書き下すだけにする。
位置と運動量
\(x_i\)を直交座標の位置座標、\(p_i\)を\(x_i\)に対応する運動量とする。2粒子なら\(2\times 3\)の6成分、3粒子なら\(3\times 3\)の9成分ある。\(n\)粒子系なら\(3n\)成分ある。任意の状態\(\lambda\)での位置の確率分布\(P(x_1,x_2,\cdots;\lambda)\)、運動量の確率分布\(P(p_1,p_2,\cdots;\lambda)\)に対して \begin{equation} P(x_1,x_2,\cdots;\lambda)=|\psi(x_1,x_2,\cdots;\lambda)|^2\qquad P(p_1,p_2,\cdots;\lambda)=|\varphi(p_1,p_2,\cdots;\lambda)|^2 \label{jo7} \end{equation} \begin{equation} \psi(x_1,x_2,\cdots;\lambda)=\sum_{p_1,p_2,\cdots} U(x_1,p_1)U(x_2,p_2)\cdots\varphi(p_1,p_2,\cdots;\lambda) \label{jo8} \end{equation} を満たす\(\psi(x_1,x_2,\cdots;\lambda),\varphi(p_1,p_2,\cdots;\lambda)\)と状態によらないユニタリー行列\(U(x_i,p_i)\)が存在する。
エネルギー
又、 エネルギー\(\varepsilon\)の測定状態、これも状態の一つだから、この状態に対応する、(\ref{jo7}),(\ref{jo8})を満たす位置の確率振幅があり、それを \[ k(x_1,x_2,\cdots;\varepsilon) \] としよう。これはユニタリー行列になる。そして任意の状態\(\lambda\)でのエネルギーの確率振幅を \[ \psi(\varepsilon;\lambda)\equiv\sum_{x_1,x_2,\cdots} k^*(x_1,x_2,\cdots;\varepsilon)\psi(x_1,x_2,\cdots;\lambda) \] と定義すると、この絶対値の2乗はエネルギーの確率分布に等しくなる。つまり \[ P(\varepsilon;\lambda)=|\varphi(\varepsilon;\lambda)|^2 \] となる。
角運動量
角運動量でも同様である。角運動量の\(z\)成分が\(l_{z1},l_{z2},\cdots\)である測定状態――\(l_{z1}\)は1番目の粒子の角運動量の\(z\)成分、\(l_{z2}\)は2番目の粒子の角運動量の\(z\)成分、という意味――の位置の確率振幅を極座標でそれぞれ\((r_1,\theta_1,\phi_1),(r_2,\theta_2,\phi_2),\cdots\)で表すと、 \[ k(\phi_1;l_{z1})\cdot k(\phi_2;l_{z2})\cdots\psi(r_1,\theta_1)\psi(r_2,\theta_2)\cdots \] となる。 \(k(\phi_i;l_{zi})\)はユニタリー行列になる。これも数学的事実ではなく、確率分布の持つ性質である。そして任意の状態\(\lambda\)での角運動量の確率振幅を \[ \varphi(r_1,\theta_1,l_{z1},r_2,\theta_2,l_{z2},\cdots;\lambda)\equiv \sum_{\phi_1,\phi_2,\cdots}k^*(\phi_1;l_{z_1})k^*(\phi_2;l_{z_2})\cdots\psi(r_1,\theta_1,\phi_1,r_2,\theta_2,\phi_2,\cdots;\lambda) \] と定義する。この確率振幅の絶対値の2乗は確率分布に等しくなる。つまり式で書くと \[ P(r_1,\theta_1,l_{z1},r_2,\theta_2,l_{z2},\cdots;\lambda)=|\varphi(r_1,\theta_1,l_{z1},r_2,\theta_2,l_{z2},\cdots;\lambda)|^2 \] となる。
1.7節 スピン変数も含めた確率振幅
今までスピンを無視してきたが、粒子はスピンという角運動量を持つ。今まで確率分布\(P(x,y,z)\)などとして話をしてきたが、これは正確ではない。実際は測定変数としてスピンを加えなければならない。それを\(s\)と書くと \[ P(x,y,z,s) \] が正確な確率分布である。\(P(x,y,z)\)として意味をなすのは、スピンの状態を暗黙のうちに指定しているか、位置の確率がスピンに依存しない場合である。どちらの場合も何らかのスピンの状態を指定しているのである。
さて、スピンを加えることは1粒子での話を2粒子や多粒子に拡張した場合とだいたい同じである。 とりあえず、粒子の位置を無視し、スピンのみに着目した確率分布、確率振幅を考える。そして簡単なのでスピン1/2の系――スピン1の系というのもあるのだが――を考えることにする。スピン1/2の系では、ある向きのスピンを測ると\(\hbar/2\)か\(-\hbar/2\)という測定値しか現れない。これはどの向きで測っても同じことで、他の向きで測っても\(\hbar/2\)か\(-\hbar/2\)しか現れない。今までの位置や運動量などの物理量に対応するのは、このどこかの向きのスピンである。そういう意味で――向きというのは無限にあるので――物理量は無限にあるということになる。ここらへんは第3章の冒頭でもう少し詳しく述べる。今任意の状態\(\lambda\)での\(z\)方向のスピンの確率分布\(P(s_z;\lambda)\)、\(x\)方向のスピンの確率分布\(P(s_z;\lambda)\)に対して――\(s_z\)、\(s_x\)は\(\hbar/2\)か\(-\hbar/2\)を取る―― \[ P(s_z;\lambda)=|\psi(s_z;\lambda)|^2\qquad\qquad P(s_x;\lambda)=|\varphi(s_x;\lambda)|^2 \] \[ \varphi(s_x;\lambda)=\sum_{s_z}U(s_x,s_z)\psi(s_z;\lambda) \] を満たす、\(z\)方向の確率振幅\(\psi(s_z;\lambda)\)、\(x\)方向の確率振幅\(\varphi(s_x;\lambda)\)、及びユニタリー行列\(U(s_x,s_z)\)が存在する。 これはあくまで位置などを省略した書き方であり、正確には \[ \varphi(x,y,z,s_x;\lambda)=\sum_{s_z}U(s_x,s_z)\psi(x,y,z,s_z;\lambda) \] ということである。これを更に運動量に変換すれば \[ \varphi(p_x,p_y,p_z,s_x;\lambda)=\sum_{s_z}U(s_x,s_z)\sum_{x,y,z}U(p_x,x)U(p_y,y)U(p_z,z)\psi(x,y,z,s_z;\lambda) \] となる。又位置と運動量の変換はスピン変数が省略されているのであって、正確には \[ \varphi(p_x,p_y,p_z,s_z;\lambda)=\sum_{x,y,z}U(p_x,x)U(p_y,y)U(p_z,z)\psi(x,y,z,s_z;\lambda) \] ということである。
以上で確率振幅、変換行列の導入は終了である。説明としては1粒子の場合から、多粒子系に移り、さらに実はスピンというものもあるのだという方向で進んだ。同種粒子系の説明は割愛した。全体としては統一した説明にはなっていない――特に角運動量が――と思う。やはり、それは、以前述べたように、私の理解不足と確率振幅というものの不自然さによるのだと思う。
1.8節 時間発展方程式
確率分布の時間発展は一意的に決まるのだが、その方程式はややこしい。しかしエネルギーの確率振幅の時間発展方程式は単純である。エネルギーの確率振幅で状態は完全に決まる。つまり変換行列によって他の物理量の確率振幅が決まり、そして確率分布も決まる。
エネルギーの時間発展方程式
エネルギー\(\varepsilon\)の確率振幅\(\varphi_\varepsilon\)の時間発展は \begin{equation} i\hbar\frac{d\varphi_\varepsilon}{dt}=\varepsilon\varphi_\varepsilon \label{c1} \end{equation} という線形方程式で決まる。尚、エネルギーの確率振幅は縮退している場合もあるし、エネルギーの測定値はあらゆる値が現れるわけではない。式(\ref{c1})の解\(\varphi_\varepsilon(t)\)は初期条件として\(t=0\)のとき\(\varphi_\varepsilon(0)\)とすると \[ \varphi_\varepsilon(t)=\exp\left({-i\frac{\varepsilon}{\hbar}t}\right)\varphi_\varepsilon(0) \] となる。
他の物理量の時間発展方程式
(\ref{c1})はエネルギーの確率振幅の方程式だが他の物理量の確率振幅の方程式に書き換えるのは、線形代数や微分方程式の教科書に書いてあるとおりである。つまり例えば位置の確率振幅を\(\psi_x\)とし、位置からエネルギーの確率振幅への変換が \[ \varphi_\varepsilon=\sum_x U_{\varepsilon x}\psi_x \qquad\qquad\qquad\left(\varphi=U\psi\right) \] だとすると――右のカッコの中は添字を省いた略記法――これを(\ref{c1})に代入して \[ i\hbar\sum_x U_{\varepsilon x}\frac{d\psi_x}{dt}=\varepsilon\sum_x U_{\varepsilon x}\psi_x \qquad\qquad\qquad\left(i\hbar U\frac{d\psi}{dt}=E U\psi\right) \] となる。ここでカッコの中の式の\(E\)というのは対角成分がエネルギー\(\varepsilon\)である行列\(E\equiv \varepsilon\delta_{\varepsilon\varepsilon'}\)のこと。これに\(U_{\varepsilon x'}^*\)を掛けて\(\varepsilon\)について和を取ると \[ i\hbar \sum_{\varepsilon,x}U_{\varepsilon x'}^*U_{\varepsilon x}\frac{d\psi_x}{dt}=\sum_\varepsilon U_{\varepsilon x'}^*\varepsilon\sum_x U_{\varepsilon x}\psi_x \qquad\qquad \left(i\hbar U^\dagger U\frac{d\psi}{dt}=U^\dagger E U\psi\right) \] となる。 \[ \sum_\varepsilon U_{\varepsilon x'} U_{\varepsilon x}=\delta_{x'x} \] なので、 これは \[ i\hbar\frac{d\psi_{x'}}{dt}=\sum_x\left(\sum_\varepsilon U^*_{\varepsilon x'}\varepsilon\; U_{\varepsilon x}\right)\psi_x \qquad\qquad \left(i\hbar\frac{d\psi}{dt}=U^\dagger E U\psi\right) \] となる。ここで\(H_{x'x}\)を \[ H_{x'x}\equiv \sum_\varepsilon U^*_{\varepsilon x'}\varepsilon \;U_{\varepsilon x} \qquad\qquad\left(H\equiv U^\dagger E U\right) \] と定義すると \[ i\hbar\frac{d\psi_{x'}}{dt}=\sum_x H_{x'x}\psi_x \qquad\qquad \left(i\hbar\frac{d\psi}{dt}=H\psi\right) \] と書ける。\(H_{x'x}\)をハミルトニアン行列、又は単にハミルトニアンという。これは位置表示のハミルトニアン行列である。他の表示、例えば運動量表示でのハミルトニアン行列も同様に定義される。ただ、変換行列の部分が位置からエネルギーの\(U_{\varepsilon x}\)でなくて、\(U_{\varepsilon p}\)に変わるだけである。 エネルギー表示のハミルトニアン行列は対角行列でその成分は測定変数の\(\varepsilon\)である。
尚、このハミルトニアン行列はエルミート行列になる。エルミート行列というのは、それの転置共役がそれ自身と等しい、つまり \[ H_{\alpha\beta}=H_{\beta\alpha}^* \] となる行列のことである。エルミート行列となる証明をしよう。簡単である。 \begin{eqnarray} H_{\beta\alpha}^*&=&\left(\sum_\varepsilon U^*_{\varepsilon\beta}\varepsilon\; U_{\varepsilon\alpha}\right)^*\notag\\ \notag &=&\sum_\varepsilon U_{\varepsilon\beta}\varepsilon \;U_{\varepsilon\alpha}^*\\ &=&\sum_\varepsilon U_{\varepsilon\alpha}^*\varepsilon\; U_{\varepsilon\beta}\notag\\ &=&H_{\alpha\beta}\notag \end{eqnarray} というわけである。 ここでエネルギー\(\varepsilon\)は実数であることを使った。添字を略すと \begin{eqnarray} H^\dagger&=&\left(U^\dagger E U\right)^\dagger\notag\\ &=&U^\dagger E U\notag\\ &=&H\notag \end{eqnarray} ということで、こちらの方が見やすい。
確率分布のままでは時間発展方程式が複雑になってしまう。エネルギーの確率分布の時間発展は \[ \frac{dP(\varepsilon)}{dt}=0 \] であるが、位置や運動量の確率分布の \(\frac{dP(x)}{dt},\frac{dP(p)}{dt}\)などは、複雑すぎて書き下せない。 確率振幅などという2次的なものを導入せざるを得ない理由の1つがここにある。
このように確率分布の時間発展は確率振幅を通してわかるのだが、その初期状態をどうやって知るのだろうか。今、ここにある粒子が、一体どういう確率分布の状態にあるのか。それがわからなければ確率分布の時間発展方程式も意味がないではないか。 測定の直後には測定状態に飛び移るのでわかるのだが、それ以外は難しい問題であり明確な答えはない。又、測定の直後はわかると言っても実際は測定には幅があり、どのような状態に移るのかは正確にはわからないのである。
1.9節 測定変数の一部の測定
状態が2つ以上の測定変数の確率振幅で表されているとき、そのうちの1つを測ったとき、状態はどんな状態に飛び移るのだろうか。例えば電子と陽子の系では電子の位置と陽子の位置という測定変数での確率振幅で状態は表されるわけだが、そのどちらか一方の位置を測ったとき、ある測定値を得る確率はどうなのだろうか。そして状態はどういう状態にどび移るのだろうか。又、 位置自体も3つの測定変数に分かれるのだが、そのうちの一つだけを測定したらどうなるのだろうか。
今電子と陽子の2粒子系を考え、電子の位置\(x\)と陽子の位置\(y\)の確率振幅\(\psi(x,y)\)のとき、電子の位置のみを測って、位置が\(x'\)である確率\(P(x')\)はどれだけなのだろうか。常識的に考えれば、電子の位置が\(x'\)で陽子の位置はどこか任意の位置である確率をすべて足し合わせたものであろう。つまり \[ P(x')=\sum_yP(x',y)=\sum_y |\psi(x',y)|^2 \] となろう。では電子の位置が\(x'\)とわかったなら、確率振幅はどういう状態に収縮するのだろうか。 まず言えそうなのは、電子の位置が\(x'\)でないものは消えるということである。陽子の位置に関しての確率振幅についてはそのままで変化しないと考えてみよう。つまり測定後の確率振幅\(\psi_後(x,y)\)は \[ \psi_後(x,y)=\left\{ \begin{array}{ll} \psi(x',y)\qquad\qquad &x=x'\text{のとき}\\ 0&x\ne x'\text{のとき} \end{array} \right. \] となるとしてみよう。 ただこれでは規格化されていないので、規格化因子を掛けなければならない。規格化因子は \[ \frac{1}{\sqrt{\sum_y |\psi(x',y)|^2}} \] であり、これは \[ \frac{1}{\sqrt{P(x')}} \] に等しい。今の議論が、特に電子の位置や陽子の位置などでなく、どんな場合でも成り立つと考えるなら、一般に
\(x,y\)を測定変数として、確率振幅が\(\psi(x,y)\)の状態のとき\(x\)について測定した結果、測定値が\(x'\) である確率\(P(x')\)は \[ P(x')=\sum_yP(x',y)=\sum_y |\psi(x',y)|^2 \] 確率振幅\(\psi_後(x,y)\)は \[ \psi_後(x,y)=\left\{ \begin{array}{ll} \frac{1}{\sqrt{P(x')}}\;\psi(x',y)\qquad\qquad &x=x'\text{のとき}\\ 0&x\ne x'\text{のとき} \end{array} \right. \] に収縮する。
と考えられる。しかし普通に考えれば、電子の位置を測れば陽子の位置にも影響を及ぼすはずであり、単純に消えるとは考えづらい。そういう疑問もあるが電子と陽子が十分離れている場合などは正しいであろう。
電子の位置と陽子の位置を同時に測りその測定値が\(x',y'\)である確率は \begin{equation} |\psi(x',y')|^2 \label{d0} \end{equation} であるわけだが、これは電子の位置を測り測定値が\(x'\)で、かつその直後に陽子の位置を測りその測定値が\(y'\)である確率と等しくなっているはずである。それが今の考えで成り立つことを確かめよう。最初の測定で電子の位置が\(x'\)である確率を\(P(x')\)とすると、その直後に陽子の位置を測り、\(y'\)である確率は \[ \frac{1}{P(x')}|\psi(x',y')|^2 \] であった。だから、測定値が\(x'\)で、その直後の測定で\(y'\)である確率は \[ P(x')\times \frac{1}{P(x')}|\psi(x',y')|^2=|\psi(x',y')|^2 \] である。これは、同時に測った場合の式(\ref{d0})と等しくなり矛盾はないわけである。
1.10節 実験で確率分布を求めるに際しての困難
今まで確率分布が与えられたものとして話を進めてきたが、その確率分布というものをどうやって知るというのだろうか。 確率分布を求めるためには 同じ状態で何度も測定を繰り返さなければならない。 そのためには 今回の実験が前と同じ状態にいるということがわかっていなければならない。 いったい、どうやって同じ状態であるということ知ることができるのか。測定の直後に限って言えば測定状態に飛び移るということになっているので、この場合は今どういう状態にいるかはわかる。ただ測定状態以外の状態ではわからない。可能な限り同じ状況を作って測定するしかなかろう。ここらへんはわからない問題である。しかしこのことを突っ込んで考えても先に進めないのでこういう根本的な問題があるということだけ頭においておこう。スピン1/2の系では、実験で確率分布を求めることができる。具体的な実験法は磁場で分離し測定状態を作り、その状態であらゆる方向でのスピンを測ることである。詳しくは第7章を見て欲しい。スピンの状態は、すべての状態がどこかの方向の測定状態であるという特別な理由があるので可能なのである(3.1節参照)。 この困難は第4章で述べる固有ベクトル法で求めた変換行列が正しいかを実験的に確かめる際にも生じるものである。