第5章 平均値と古典論の運動方程式の形式的一致
この章では、固有ベクトル法で求めた変換行列を使えば、量子力学の平均値の時間発展方程式が形式的には古典論と一致することを数学的に示す。形式的に一致しているからと言って、 波束が古典力学の方程式に従って動くとは言えないが、 一般には磁場、電場の変化が空間上の変化が波束に比べて小さいなら、平均値は古典力学の方程式に従う。まず平均値の時間発展方程式の一般式を示し、それを適用して順次、特殊から一般へと進んでいく。まずは 第4章の宿題であった \(m_i\frac{d\left\langle x_i\right\rangle }{dt}=\left\langle p_i\right\rangle \), \(\frac{d\left\langle p_i\right\rangle }{dt}=-\left\langle \frac{\partial\, V}{\partial\, x_i}\right\rangle \) が成り立つことを証明する。 次に磁場のある場合、つまりベクトルポテンシャルの存在する系でも、古典論と形式上一致することを示す。最後に任意の物理量でも 平均値の運動方程式は古典論と形式上一致することを示す。これからは演算子記号\(\hat{p}\)の上に付けたものを省いて単に\(p\)と書くことにするが、混乱することはないと思う。
5.1節 平均値の運動方程式の一般形
第4章で各物理量ごとに、位置の確率振幅に作用させる演算子を定義した。その演算子の位置以外の確率振幅に作用させる場合での表示というものを考えたい(注 既に第4章でエネルギー演算子の、位置表示だけでなく、エネルギー表示などについても述べたが、ここで改めて考えようということである。 )。線形代数学でよく知られているように、線形演算子\(B\)の他の表示への変換は、\(U\)を他の表示への変換行列として、\(UBU^{-1}\)であるのだが、そのことについて少し注意したい。 まず、位置の確率振幅に演算子\(B\)をほどこした\(B\psi\)というのは、絶対値の2乗が1にはならないので、確率振幅でも何でもなく、物理的実体のないものである。 通常、線形代数学の線形演算子は、あるベクトル空間から、あるベクトル空間への写像であり、写像するベクトル空間という実体がある。 そこが線形代数学の線形演算子とは違うところである。 例えばあるベクトル\(\vec{x}\)に角度\(\theta\)だけ回転させる演算子\(T(\theta)\)を作用させた\(T(\theta)\vec{x}\)というのは実体がある。 だから基底の変更による演算子の行列表示の変更は、ベクトルがどの基底であろうが同じ回転をしなければいけないということから決まるのである。しかし\(B\psi\) は実体がない。例えば位置表示において、運動量演算子を作用させた \(\frac{\hbar}{i}\frac{\partial\,}{\partial\, x_i}\psi(x)\) というのが、もしある量子力学的状態(確率分布の組のこと)を表していると言うなら、これを、例えばエネルギー表示の確率振幅で表すことはできる。しかし\(\frac{\hbar}{i}\frac{\partial\,}{\partial\, x_i}\psi(x)\)はいかなる量子力学的状態も表していないのであるから他の表示も何もないのである。 それでは、この演算子\(B\)は表示の変更というものを考えることができないのかというと、そんなことはない。いろいろ難しいことを考えず、単に 写像された\(B\psi\)を物理的意味のない単なる数ベクトルと考えれば、基底の変換による演算子の表示の変換が考えられる。そして演算子の表示の変換は線形代数学のように\(UBU^{-1}\)となる。 量子力学での確率振幅の変換行列は必ずユニタリーなので \(UBU^\dagger\)となる。
さて、よく知られているように \[ \psi^\dagger B \psi \] はユニタリー変換 \begin{equation} \psi'=U\psi \label{122} \end{equation} で不変量になる。これは線形代数学でよくする添字省略形である。 この証明は簡単で、確率振幅が(\ref{122})と変換されるなら、演算子\(B\)は \[ B'=UBU^\dagger \] と変換されるので、 \begin{eqnarray*} \psi'^\dagger B'\psi'&=&\left(U\psi \right)^\dagger\left(UBU^\dagger\right)\left(U\psi\right)\\ &=& \psi^\dagger U^\dagger UB U^\dagger U\psi\\ &=& \psi^\dagger B\psi \end{eqnarray*} となるというわけである。
4.2節の命題4.2で述べたように、演算子\(B\)の\(B\)表示は対角成分が固有値\(b\)――――これは取りうる測定値でもある――――となる対角行列、つまり \[ B_{b'b}=b'\delta_{b'b} \] となる。だから、この\(\psi^\dagger B\psi\)を物理量\(B\)の表示で計算すると \[ \psi^\dagger B\psi=\sum_{b',b}\psi^*_{b'} B_{b'b}\psi_b=\sum_b b\left|\psi_b\right|^2 \] となる。これは物理量\(B\)の平均値である。ここで注意だが、\(\psi^\dagger B \psi\)が平均値となるのは\(B\)がエルミート演算子の場合である。エルミートでないなら――――必ずしもとはいえないが――――\(B\)は対角成分が実数固有値の対角行列にならないだろうから平均値にならない。例えば、\(yp_y\)などは、エルミートではない。というよりも\(yp_y\)などは測定することができないはずである。以上のことを まとめると
命題5.1 \(B\)を物理量\(B\)の演算子として、エルミート演算子とすると、 \( \psi^\dagger B \psi \) は、どんな表示でも、状態が確率振幅\(\psi\)のときの物理量\(B\)の平均値となる。つまり \[ \psi^\dagger B \psi=\left\langle B\right\rangle \] となる。
さて、これを使って 平均値の時間発展方程式の一般形を導こう。 \begin{equation} \frac{d\left\langle B\right\rangle }{dt}=\frac{d}{dt}\left(\psi^\dagger B\psi\right) =\frac{d\psi^\dagger}{dt} B\psi+\psi B\frac{d\psi}{dt}+\psi^\dagger \frac{\partial\, B}{\partial\, t}\psi \label{k1} \end{equation} であるが(注 物理量\(B\)が時間を含んでいる場合を扱うことなどないのだが、時間を含んでいたからと言ってたいしてややこしくなることもないので、時間を含むとした。)一方\(\psi\)の時間発展は \[ i\hbar\frac{d\psi}{dt}=H\psi \] で決まる。ここで\(H\)はハミルトニアン行列。 これの転置共役をとると \[ -i\hbar \frac{d\psi^\dagger}{dt}=\psi^\dagger H \] である。ここで\(H\)がエルミートであることを使った。これを(\ref{k1})に代入すると \begin{eqnarray*} \frac{d\left\langle B\right\rangle }{dt}&=&-\frac{1}{i\hbar}\left(\psi^\dagger HB\psi-\psi^\dagger BH\psi\right)+\psi^\dagger \frac{\partial\, B}{\partial\, t}\psi\\ &=&\psi^\dagger\left(\frac{1}{i\hbar}[B,H]+\frac{\partial\, B}{\partial\, t}\right)\psi \end{eqnarray*} となる。ここで\([B,H]=BH-HB\)のことである。これは交換子と呼ばれるもので、\(A,B\)を演算子として \[ [A,B]\equiv AB-BA \] と定義される。 さて、この結果は今から頻繁に使うので命題の形で書いておこう。
命題5.2 確率振幅\(\psi\)での物理量Bの平均値の時間発展は、 \[ \frac{d{\left\langle B\right\rangle }}{dt}=\psi^\dagger\left(\frac{1}{i\hbar}[B,H]+\frac{\partial\, B}{\partial\, t}\right)\psi \] が成り立つ。
尚、\(\frac{1}{i\hbar}[B,H]\)と\(\frac{\partial\, B}{\partial\, t}\)はエルミートなので \[ \frac{d{\left\langle B\right\rangle }}{dt}=\left\langle \frac{1}{i\hbar}[B,H]\right\rangle +\left\langle \frac{\partial\, B}{\partial\, t}\right\rangle \] でもある。交換子の性質
交換子のいくつかの性質を述べよう。\(A,B,C\)を演算子として、定義から明らかに \[ [A+B,C]=[A,C]+[B,C]\qquad [A,B+C]=[A,B]+[A,C]\qquad \] が成り立つ事がわかる。 そして \begin{equation} [A,B^2]=[A,B]B+B[A,B] \label{A} \end{equation} が成り立つ。 この性質は今後度々使う。また、 \begin{equation} [x_i,p_j]=i\hbar\delta_{ij} \label{B} \end{equation} である。これ は位置表示で演算子\(x_i=x_i,\;p_i=\frac{\hbar}{i}\frac{\partial\,}{\partial\, x_i}\)であることを使えば明らかであろう。 尚、この交換関係は他の表示でも成り立つ。
5.2節 平均値の運動方程式が正準方程式を満たすこと――――磁場がない場合
これで準備ができたので、\(m_i\frac{d\left\langle x_i\right\rangle }{dt}=\left\langle p_i\right\rangle \), \(\frac{d\left\langle p_i\right\rangle }{dt}=-\left\langle \frac{\partial\, V}{\partial\, x_i}\right\rangle \)が成り立つことを証明しよう。これ以後、演算子は基本的に位置表示のものを使うとする。系の古典力学でのハミルトニアン\(H\)は \[ H=\sum_i\frac{p_i^2}{2m_i}+V(x) \] だとしよう。ベクトルポテンシャルを含んでいる場合は5.3節で証明する。第4章の命題4.1で述べたように、量子論での位置表示のハミルトニアン\(H\)は単にこれを\(x_i=x_i,\;p_i=\frac{\hbar}{i}\frac{\partial\,}{\partial\, x_i}\)で置き換えたものになる。だからこれ自身が量子論でのハミルトニアン行列になる。
位置の時間発展
まず \begin{equation} \frac{d\left\langle x_i\right\rangle }{dt}=\frac{\left\langle p_i\right\rangle }{m_i} \label{C} \end{equation} から証明する。これは命題5.2より \[ \frac{d\left\langle x_i\right\rangle }{dt}= \psi^\dagger\left(\frac{1}{i\hbar}[x_i,H]\right)\psi \] なので \begin{equation} [x_i,H]=i\hbar\frac{ p_i}{m_i} \label{kou1} \end{equation} が成り立つことを示せればよい。 実際 \[ [x_i,H]=[x_i,p_i^2/2m_i] \] であり、(\ref{A}),(\ref{B})より \[ [x_i,p_i^2]=[x_i,p_i]p_i+p_i[x_i,p_i]=2i\hbar p_i \] である。よって(\ref{kou1})が成り立つ。よって(\ref{C})が成り立つ。
運動量の時間発展
又、 \begin{equation} \frac{d\left\langle p_i\right\rangle }{dt}=-\left\langle \frac{\partial\, V}{\partial\, x_i}\right\rangle \label{D} \end{equation} を証明するには、命題5.2より、 \[ \frac{d\left\langle p_i\right\rangle }{dt}=\psi^\dagger\left(\frac{1}{i\hbar}[p_i,H]\right)\psi \] なので、 \[ [p_i,H]=-i\hbar \frac{\partial\, V}{\partial\, x_i} \] であることを証明できれば良い。これは \[ [p_i,H]=[p_i,V(x)]=-i\hbar\frac{\partial\, V}{\partial\, x_i} \] となるので成り立つ。よって(\ref{D})は成り立つ。
今は固有ベクトル法で決まる変換行列の正しさを見るために古典論と対比しているのだが、この証明では変換行列の成分の具体的な値など使っておらず、演算子の交換関係しか使っていないように見える。しかし、この証明には命題5.2,命題5.1が必要であり、命題5.1の証明では演算子\(B\)が\(B\)表示で対角行列になることを使っている。対角行列になるというのは、固有ベクトルが変換行列になるということを使っているのである。しかしながら、具体的な変換行列の成分については何も使っていない。その情報は交換子\([x,H]\)や\([p,H]\)の中に含まれているはずである。
5.3節 磁場のある場合も正準方程式を満たすこと
次に、磁場のある場合も平均値の運動方程式は、形式的には正準方程式を満たすことを示す。 これは今までの場合と何が違うかと言うと、古典力学におけるハミルトニアンが \[ H=\sum_{i=1}^{i=3}\frac{1}{2m}\left[p_i-\frac{q}{c}A_i(x)\right]^2+q\phi(x) \] という形だという ことである。量子力学でのハミルトニアンはここでの\(p_i\)を\(\frac{\hbar}{i}\frac{\partial\, }{\partial\, x_i}\)に置き換えたものになる。これは1粒子の場合だが、2粒子以上でも粒子数に応じて、同じ項が加わるだけなので1粒子の場合を考える。これはCGSガウス単位系であり、\(q\)は電荷、\(c\)は光速、\(A\)はベクトルポテンシャル、\(\phi\)はスカラーポテンシャルである。\(A_i(x)\)と\(\phi(x)\)は時間を陽に含んでおらず位置のみの関数で(注 \(A\)や\(\phi\)が時間を陽に含んでいると、ハミルトニアンまで時間を陽に含むことになってしまう。そうなると命題5.2なども成り立たなくなってしまう。この論文では一貫してハミルトニアンは時間を含まないものとして扱う。 )、今後は単に\(A_i,\phi\)と書くので位置のみの関数だと覚えておいてもらいたい。 このハミルトニアンを使って量子論の平均値の運動方程式と古典論の運動方程式を対比していこう。
まず、簡略化のため \[ p_i-\frac{q}{c}A_i=u_i\qquad( i=1,2,3) \] と置くことにする。これを使うとハミルトニアンは \[ H=\sum_{i=1}^{i=3}\frac{u_i^2}{2m}+q\phi(x) \] とすっきりする。後で見るように、\(u_i\)は通常の運動量\(m\cdot dx_i/dt\)である。 さて、今から古典論と量子論での、位置と運動量と加速度の時間発展方程式を対比しながら導出していくのだが、そのさい、 古典論の式では \begin{equation} \frac{\partial\, u_j}{\partial\, p_i}=\delta _{ij} \qquad \frac{\partial\, u_j}{\partial\, x_i}=-\frac{q}{c}\frac{\partial\, A_j}{\partial\, x_i} \label{126} \end{equation} を使う。量子論では \begin{equation} [x_i,u_j]=i\hbar\delta_{ij} \label{jiba-1} \end{equation} \begin{equation} [p_i,u_j]= -\frac{q}{c}[p_i,A_j] =i\hbar\frac{q}{c}\frac{\partial\, A_j}{\partial\, x_i} \label{jiba-2} \end{equation} \begin{equation} [A_i,u_j]= [A_i,p_j] = i\hbar\frac{\partial\, A_i}{\partial\, x_j} \label{jiba-3} \end{equation} を使う。また\(B\)を任意の演算子として \begin{equation} [B,u_i^2]=[B,u_i]u_i+u_i[B,u_i] \label{jiba-4} \end{equation} も使う。これは(\ref{A})で述べたものと同じである。これらが成り立つのはすぐわかろう。
位置古典論
まず位置\(x_i\)の時間発展方程式は、古典論では正準方程式 \[ \frac{d x_i}{dt}=\frac{\partial\, H}{\partial\, p_i} \] より
\begin{equation} m\frac{dx_i}{dt}=u_i\quad\quad \left(u_i=p_i-\frac{q}{c}A_i\right) \label{ik} \end{equation}
である。尚、この式から\(p_i\)は \[ p_i=m\frac{dx_i}{dt}+\frac{q}{c}A_i \] となり通常の運動量と異なることに注意。ベクトルポテンシャルが空間で変化する場合など一体どうやってこの運動量と言われるものを測るのだろうかとは思う。
位置量子論
一方量子論だが、命題5.2より \[ \frac{d\left\langle x_i\right\rangle }{dt}=\psi^\dagger \frac{[x_i,H]}{i\hbar}\psi \] である。そして \[ [x_i,H]=\frac{1}{2m}\left[x_i,u_i^2\right] \] であり、(\ref{jiba-4})、(\ref{jiba-1})より \[ \left[x_i,u_i^2\right]= [x_i,u_i]u_i+u_i[x_i,u_i] =2i\hbar u_i \] なので
\begin{equation} m\frac{d\left\langle x_i\right\rangle }{dt}=\left\langle u_i\right\rangle \quad\quad \left(u_i=p_i-\frac{q}{c}A_i\right) \label{ir} \end{equation}
である。これは古典論での(\ref{ik})と同じ項で構成されている。
運動量古典論
運動量の時間発展方程式は、古典論では正準方程式 \[ \frac{d p_i}{dt}=-\frac{\partial\, H}{\partial\, x_i} \] より、(\ref{126})を使って
\begin{equation} \frac{dp_i}{dt}=\frac{q}{mc}\sum_{j=1}^{3}u_j\cdot \frac{\partial\, A_j}{\partial\, x_i}-q\frac{\partial\, \phi}{\partial\, x_i}\quad\quad \left(u_i=p_i-\frac{q}{c}A_i\right) \label{uk} \end{equation}
となる。
運動量量子論
量子論を計算する。命題5.2より \[ \frac{d\left\langle p_i\right\rangle }{dt}=\psi^\dagger \frac{[p_i,H]}{i\hbar}\psi \] である。そして \[ [p_i,H]=\sum_{j=1}^3\frac{1}{2m}\left[p_i,u_j^2\right]+\left[p_i,q\phi\right] \] であり、(\ref{jiba-4})、(\ref{jiba-2})より \begin{eqnarray*} \left[p_i,u_j^2\right]&=& \left[p_i,u_j\right]u_j+u_j\left[p_i,u_j\right]\\ &=&i\hbar\frac{q}{c}\frac{\partial\, A_j}{\partial\, x_i}\cdot u_j+u_j\cdot i\hbar\frac{q}{c}\frac{\partial\, A_j}{\partial\, x_i} \end{eqnarray*} となる。また \[ [p_i,q\phi]=-i\hbar q\frac{\partial\, \phi}{\partial\, x_i} \] である。だから
\begin{equation} \frac{d\left\langle p_i\right\rangle }{dt} =\frac{q}{2mc}\sum_{j=1}^3\left\langle \frac{\partial\, A_j}{\partial\, x_i}\cdot u_j + u_j\cdot\frac{\partial\, A_j}{\partial\, x_i}\right\rangle - q\left\langle \frac{\partial\, \phi}{\partial\, x_i}\right\rangle \quad \quad\left(u_i=p_i-\frac{q}{c}A_i\right) \label{ur} \end{equation}
である。 これも、演算子の順序を気にしなければ古典論の(\ref{uk})と同じ項で構成されている。 ただ \[ \frac{\partial\, A_j}{\partial\, x_i}\cdot u_j \ne u_j\cdot\frac{\partial\, A_j}{\partial\, x_i} \] であることに注意(注 \(\frac{\partial\, A_j}{\partial\, x_i}\cdot u_j\)はエルミートでないので、これの平均\(\left\langle \frac{\partial\, A_j}{\partial\, x_i}\cdot u_j\right\rangle \)というのは考えることができない。それで、\(\left\langle \frac{\partial\, A_j}{\partial\, x_i}\cdot u_j + u_j\cdot\frac{\partial\, A_j}{\partial\, x_i}\right\rangle \)とした。 )。
加速度古典論
さて次に加速度だが、古典論では(\ref{ik})を時間微分して \[ m\frac{d^2 x_i}{dt^2} =\frac{dp_i}{dt}-\frac{q}{c}\frac{dA_i}{dt} \] である。ベクトルポテンシャルの時間微分は \begin{eqnarray} \frac{dA_i}{dt} &=& \sum_{j=1}^3\frac{\partial\, A_i}{\partial\, x_j}\frac{dx_j}{dt}\notag \\ &=& \sum_{j=1}^3\frac{\partial\, A_i}{\partial\, x_j}\frac{u_j}{m} \label{bk} \end{eqnarray} である。ここで(\ref{ik})を使った。又、運動量の時間微分は(\ref{uk})である。これらを代入すると \[ m\frac{d^2 x_i}{dt^2} =\frac{q}{mc}\sum_{j=1}^{3}\left(\frac{\partial\, A_j}{\partial\, x_i}-\frac{\partial\, A_i}{\partial\, x_j}\right)u_j-q\frac{\partial\, \phi}{\partial\, x_i} \] となる。ここで \begin{equation} \frac{\partial\, A_j}{\partial\, x_i}-\frac{\partial\, A_i}{\partial\, x_j}=F_{ij}\qquad\qquad -\frac{\partial\, \phi}{\partial\, x_i}=E_i \label{126a} \end{equation} と置き、(\ref{ik})を使うと
\begin{equation} m\frac{d^2 x_i}{dt^2} =\frac{q}{c}\sum_{j=1}^{3} F_{ij}\frac{dx_j}{dt} + qE_i \label{kk-2} \end{equation}
となる。尚、\(F_{ij}\)は磁場テンソルと言われるもので、磁場\(B_i\)とは \[ F_{12}=B_3\qquad F_{23}=B_1\qquad F_{31}=B_2 \] という関係にある。\(E_i\)は電場である。そしてこの式はローレンツ力の式になっている。
加速度量子論
一方量子論では(\ref{ir})を時間微分して \[ m\frac{d^2\left\langle x_i\right\rangle }{dt^2} = \frac{d\left\langle p_i\right\rangle }{dt}-\frac{q}{c}\frac{d\left\langle A_i\right\rangle }{dt} \] である。ベクトルポテンシャルの時間微分だが、命題5.2より \[ \frac{d\left\langle A_i\right\rangle }{dt}=\psi^\dagger \frac{[A_i,H]}{i\hbar}\psi \] である。そして \[ [A_i,H] = \frac{1}{2m}\sum_{j=1}^3\left[A_i,u_j^2\right] \] であり、(\ref{jiba-4})、(\ref{jiba-3})より \begin{eqnarray} \left[A_i,u_j^2\right] &=& \left[A_i,u_j\right]\cdot u_j + u_j\cdot \left[A_i,u_j\right]\notag\\ &=& i\hbar\frac{\partial\, A_i}{\partial\, x_j}\cdot u_j + i\hbar\; u_j\cdot \frac{\partial\, A_i}{\partial\, x_j}\notag \end{eqnarray} である。だから \[ \frac{d\left\langle A_i\right\rangle }{dt} = \frac{1}{2m}\sum_{j=1}^3\left\langle \frac{\partial\, A_i}{\partial\, x_j}\cdot u_j + u_j\cdot \frac{\partial\, A_i}{\partial\, x_j}\right\rangle \] これは順序以外は古典論の(\ref{bk})と同じ項で構成されている。又、運動量の時間微分は(\ref{ur})であり、これは古典論と一致していることはすでに見た。だから加速度も古典論と同じ項で構成されていることになる。長いがそれを書き下すと、 \[ m\frac{d^2\left\langle x_i\right\rangle }{dt^2} = \frac{q}{2mc}\sum_{j=1}^3\left\langle \left(\frac{\partial\, A_j}{\partial\, x_i}-\frac{\partial\, A_i}{\partial\, x_j}\right)\cdot u_j +u_j\cdot\left(\frac{\partial\, A_j}{\partial\, x_i}-\frac{\partial\, A_i}{\partial\, x_j}\right)\right\rangle - q\left\langle \frac{\partial\, \phi}{\partial\, x_i}\right\rangle \] となる。(\ref{126a})を使うと、
\[ m\frac{d^2\left\langle x_i\right\rangle }{dt^2} = \frac{q}{2mc}\sum_{j=1}^3\left\langle F_{ij}\cdot u_j +u_j\cdot F_{ij}\right\rangle + q\left\langle E_i\right\rangle \]
となる。 構成されている項は古典論と同じだが、もちろん古典論と量子論では物理的内容が異なる。第4章で述べたように、平均値\(\left\langle x\right\rangle \)の運動は古典論の方程式には従うわけではない。
波束内で電場、磁場の変化が小さい場合
これだけでは身もふたもないので、平均値の運動が古典論の方程式に従うような状況を考えよう。 まず、 \[ \left\langle F_{ij}\cdot u_j +u_j\cdot F_{ij}\right\rangle = \sum_x\psi^\dagger(x)\left(F_{ij}\cdot u_j+F_{ij}\cdot u_j-i\hbar \frac{\partial\, F_{ij}}{\partial\, x_j}\right)\psi(x) \] と変形しておこう。 今磁場\(F_{ij}\)と電場\(E_i\) が波束内での変化が十分小さく、
【1】 波束内で、常に波束の平均値\(\left\langle x\right\rangle \)での値と考えていい、つまり波
束内では\(F_{ij}(x)\simeq F_{ij}(\left\langle x\right\rangle ),E(x)\simeq E(\left\langle x\right\rangle )\)とみなせる。
【2】 波束内では磁場の空間微分\(\frac{\partial\, F_{ij}}{\partial\, x_j}\simeq 0\)とみなせる
としていいとしよう。ここで、【1】が満たされるからといって必ずしも【2】が満たされるわけではないことに注意しよう。例えば空間微分が大きくても波束が非常に小さければ、【1】は満たされるが、【2】は満たされない。さて、この条件が満たされるなら \begin{eqnarray*} \sum_x\psi^\dagger(x)\left(2F_{ij}(x)\cdot u_j-i\hbar \frac{\partial\, F_{ij}}{\partial\, x_j}\right)\psi(x) &\simeq& 2F_{ij}\big(\left\langle x\right\rangle \big)\sum_x \psi^\dagger(x)u_j\psi(x)\\ &=&2F_{ij}\big(\left\langle x\right\rangle \big)\cdot\left\langle u_j\right\rangle \end{eqnarray*} と近似できるし、 \[ \left\langle E_i\right\rangle = \sum_x\psi^*_x E_i(x)\psi_x \simeq E_i\big(\left\langle x\right\rangle \big) \] と近似できる。だから \[ m\frac{d^2\left\langle x_i\right\rangle }{dt^2} \simeq \frac{q}{mc}\sum_{j=1}^3F_{ij}\big(\left\langle x\right\rangle \big)\cdot\left\langle u_j\right\rangle + qE_i\big(\left\langle x\right\rangle \big) \] となる。又は(\ref{ir})を使って\(\left\langle u_j\right\rangle \)を消去すると \[ m\frac{d^2\left\langle x_i\right\rangle }{dt^2} \simeq \frac{q}{c}\sum_{j=1}^3F_{ij}\big(\left\langle x\right\rangle \big)\cdot\frac{d\left\langle x_j\right\rangle }{dt} + qE_i\big(\left\langle x\right\rangle \big) \] である。古典論では、(\ref{kk-2})を再掲すると、 \[ m\frac{d^2 x_i}{dt^2} =\frac{q}{c}\sum_{j=1}^{3} F_{ij}(x)\frac{dx_j}{dt} + qE_i(x) \] であった。量子論での\(\left\langle x\right\rangle \)と古典論での\(x\)は微分方程式の未知変数として全く同じ役割をしている。 だからこの場合位置の平均とその時間微分を初期条件として与えられれば、その運動は古典論の時間発展方程式に従うということである。つまり
磁場と電場が波束内で変化が十分小さく、上記条件【1】【2】が満たされるなら、位置の平均値\(\left\langle x\right\rangle \)は古典論の運動方程式に従う。
尚、この条件が満たされている場合は、波束全体の運動もおおむね古典論の方程式に従うと考えられる。 この条件が完全に満たされるのは、空間的にも時間的にも 一様な磁場、電場の場合である。この場合は近似でなく完全に位置の平均値\(\left\langle x\right\rangle \)の運動は 古典論の方程式に従う。
5.4節 任意の物理量の平均値の時間発展式が古典論と一致すること
いままで古典論と量子論で位置、運動量、加速度などの時間発展方程式での項が形式的に等しいことを見てきた。実はこのことはあらゆる物理量で――――演算子にしたときにエルミートでなければならないが――――成り立つことなのである。それを示そう。
ポアソンの括弧
古典力学では位置\(x\)、運動量\(p\)、時間\(t\)の関数である物理量\(B(x,p,t)\)の時間発展方程式は \begin{equation} \frac{dB}{dt}=\sum_i\left(\frac{\partial\, B}{\partial\, x_i}\frac{\partial\, H}{\partial\, p_i}-\frac{\partial\, B}{\partial\, p_i}\frac{\partial\, H}{\partial\, x_i}\right) +\frac{\partial\, B}{\partial\, t} \label{kj} \end{equation} と表される。この導出は簡単でまず、\(B\)を時間微分すると \[ \frac{dB}{dt}=\sum_i\left(\frac{\partial\, B}{\partial\, x_i}\frac{dx_i}{dt}+\frac{\partial\, B}{\partial\, p_i}\frac{dp_i}{dt}\right) +\frac{\partial\, B}{\partial\, t} \] となるが、正準方程より \[ \frac{dx_i}{dt}=\frac{\partial\, H}{\partial\, p_i} \qquad\qquad \frac{dp_i}{dt}=-\frac{\partial\, H}{\partial\, x_i} \] なのでこれをを代入すれば(\ref{kj})が得られる。正準方程式は\(B=x,B=p\)とした場合であるので、この時間発展方程式に含まれる。(\ref{kj})の右辺の和の項はポアソンの括弧と呼ばれるもので\(\{B,H\}\)と略記される。尚、一般に任意の物理量\(A,B\)のポアソンの括弧\(\{A,B\}\)の定義は \[ \{A,B\}\equiv\sum_i \left( \frac{\partial\, A}{\partial\, x_i}\frac{\partial\, B}{\partial\, p_i}-\frac{\partial\, A}{\partial\, p_i}\frac{\partial\, B}{\partial\, x_i} \right) \] である。
一方量子論での時間発展方程式は \[ \frac{d\left\langle B\right\rangle }{dt}=\psi^\dagger\left(\frac{1}{i\hbar}[B,H]+\frac{\partial\, B}{\partial\, t}\right)\psi \] であった(命題5.2)。この右辺の\(\frac{1}{i\hbar}[B,H]+\frac{\partial\, B}{\partial\, t}\)が(\ref{kj})の右辺と同じ項で構成されることを証明しよう。 \(\frac{\partial\, B}{\partial\, t}\)は同じなので \( \frac{1}{i\hbar}[B,H]\)が\(\{B,H\} \)と同じ項で構成されている ことを証明できればよい。 証明に際しては \(B\)と\(H\)は運動量\(p\)に関しては多項式であるものに限定する。 実際問題として、 \(H\)では位置に関しては\(1/r\)のようなポテンシャルもあるが、\(p\)の多項式となっていない\(H\)は見たことがない。それに基本的にどんな関数でも多項式で近似できるので\(p\)に関しては多項式と制限しても特に問題はなかろう。 例えばハミルトニアンが \[ H=\sum_i\frac{p_i^2}{2m_i}+V(x)\qquad\qquad H=\sum_{i=1}^{i=3}\frac{1}{2m}\left[p_i-\frac{q}{c}A_i(x)\right]^2+q\phi(x) \] のときは\(p\)の多項式になっているし、角運動量の\(z\)成分も \[ xp_y-yp_x \] と\(p\)の多項式になっている。角運動量の2乗も\(p\)の多項式である。 そういうわけで、
補題A 物理量\(C\)と\(D\)が\(p\)に関して多項式のとき、 \(\frac{1}{i\hbar}[C,D]\)は\(\{C,D\}\)と同じ項で構成されている
ことを証明すればよいことになる。
さて、\(p\)に関して多項式ということは、それは、\(p\)か位置\(x\)の関数(注 \(x\)の関数と言っても、定数や時間の関数の場合もあるので、広い意味での\(x\)の関数という意味である。正確には\(p\)を含まないという意味であるが、そうすると分かりづらいし、時間は今後役割を担わないので、位置の関数とした。今後もそういう意味で使う。)による積の和で書けるということである。つまり \(C\)が\(p\)の多項式なら、\(C\)は \[ C=\sum_i C_i \] というように、個々の\(C_i\) \[ C_i=c_1c_2\cdots c_m \] と言う積の形で書け、個々の\(c_i\)は\(p\)か位置\(x\)の関数であるような\(C_i\)の和の形で書けるということである。
さて、交換子とポアソンの括弧では、それぞれ \[ \left[\sum_iC_i,\sum_j D_j\right]=\sum_{i,j}[C_i,D_j]\qquad\qquad \left\{\sum_iC_i,\sum_j D_j\right\}=\sum_{i,j}\{C_i,D_j\} \] が成り立つ。だから個々に \( \frac{1}{i\hbar}[C_i,D_j]\)が\(\{D_i,D_j\}\) と同じ項で構成されていることが証明できればよい。 つまり、補題Aを証明することは
補題B \(C=c_1c_2\cdots c_m\)、\(D=d_1d_2\cdots d_n\)のとき \(\frac{1}{i\hbar}[C,D]\)は\(\{C,D\}\)と同じ項で構成されている。ここで\(c\)と\(d\)は\(p\)か位置\(x\)の関数である。
を証明することに帰着したわけである。
古典論の項
今例えば\(C=c_1c_2c_3\)とすると、\(\frac{\partial\, C}{\partial\, x_k}\)というものは \[ \frac{\partial\, C}{\partial\, x_k}=\frac{\partial\, c_1}{\partial\, x_k}c_2c_3+c_1\frac{\partial\, c_2}{\partial\, x_k}c_3+c_1c_2\frac{\partial\, c_3}{\partial\, x_k} \] というように個々の項の微分の和になる。同様に\(D=d_1d_2d_3\)とすると \[ \frac{\partial\, D}{\partial\, p_k}=\frac{\partial\, d_1}{\partial\, p_k}d_2d_3+d_1\frac{\partial\, d_2}{\partial\, p_k}d_3+d_1d_2\frac{\partial\, d_3}{\partial\, p_k} \] となる。だから \[ \frac{\partial\, C}{\partial\, x_k}\frac{\partial\, D}{\partial\, p_k}=\sum_{i,j}\frac{\partial\, c_i}{\partial\, x_k}\frac{\partial\, d_j}{\partial\, p_k}\times (c_i,d_jを除いた項の積) \] となる。こう考えるとポアソンの括弧は
補題C \(C=c_1c_2\cdots c_m\)、\(D=d_1d_2\cdots d_n\)のとき \begin{eqnarray*} \sum_k \left(\frac{\partial\, C}{\partial\, x_k}\frac{\partial\, D}{\partial\, p_k}-\frac{\partial\, C}{\partial\, p_k}\frac{\partial\, D}{\partial\, x_k}\right) &=& \sum_k\sum_{i,j} \left[\left(\frac{\partial\, c_i}{\partial\, x_k}\frac{\partial\, d_j}{\partial\, p_k}-\frac{\partial\, c_i}{\partial\, p_k}\frac{\partial\, d_j}{\partial\, x_k}\right) \times (c_i,d_jを除いた項の積)\right]\notag\\ &=&\sum_{i,j}\Big(\{c_i,d_j\}\times (c_i,d_jを除いた項の積)\Big) \end{eqnarray*} となる
ことがわかろう。
量子論の項
次に、量子論に移ろう。今からやる作業は簡単なことなのだが、文字で説明するのは案外難しいので、自分でやってみることを勧める。 \(C=c_1c_2c_3\)、\(D=d_1d_2d_3\)という簡単な例で考えよう。 \(c_3\)を\(d_1d_2d_3\)に作用させ、一般の公式\(xy=[x,y]+yx\)を使って順次右へ持っていくと \begin{eqnarray*} c_3d_1d_2d_3&=&\Big([c_3,d_1]+d_1c_3\Big)d_2d_3\\ &=&[c_3,d_1]d_2d_3+d_1\Big([c_3,d_2]+d_2c_3\Big)d_3\\ &=&[c_3,d_1]d_2d_3+d_1[c_3,d_2]d_3+d_1d_2[c_3,d_3]+d_1d_2d_3c_3 \end{eqnarray*} となる。ここで演算子を変数とする関数\(f(x)\)を \[ f(x)\equiv[x,d_1]d_2d_3+d_1[x,d_2]d_3+d_1d_2[x,d_3] \] と定義すると \[ c_3d_1d_2d_3=f(c_3)+d_1d_2d_3c_3 \] と書ける。\(f(x)\)というのは\(x\)と\(d_1,d_2,d_3\)の全てとの交換子を含み、それに掛かっている項は、その交換子に含まれていない項の和で構成されていることに注意しよう。さて、これに\(c_2\)を作用させ、\(d_1d_2d_3\)とだけ順次交換していくと、全く今と同様に \begin{eqnarray*} c_2c_3d_1d_2d_3&=&c_2f(c_3)+(c_2d_1d_2d_3)c_3\\ &=&c_2f(c_3)+f(c_2)c_3+(d_1d_2d_3c_2)c_3 \end{eqnarray*} となる。さらにこれに\(c_1\)を作用させて\(d_1d_2d_3\)とだけ交換していくと \begin{eqnarray*} c_1c_2c_3d_1d_2d_3&=& c_1c_2f(c_3)+c_1f(c_2)c_3+(c_1d_1d_2d_3)c_2c_3\\ &=&c_1c_2f(c_3)+c_1f(c_2)c_3+f(c_1)c_2c_3+(d_1d_2d_3c_1)c_2c_3 \end{eqnarray*} となる。だから \begin{equation} [c_1c_2c_3,d_1d_2d_3]=c_1c_2f(c_3)+c_1f(c_2)c_3+f(c_1)c_2c_3 \label{kouk} \end{equation} となる。今の作業というのはまず\(c_3\)を\(d_1d_2d_3\)と順次交換して右へ持っていき、次に\(c_2\)をこれに作用させるわけだが、交換子で構成されている\(f(c_3)\)とは交換させず、\(d_1d_2d_3\)とだけ交換し、\(c_3\)の前で止めたわけである。さらに、このことを\(c_1\)でも行ったのである。この作業を図5.1に模式的に表した
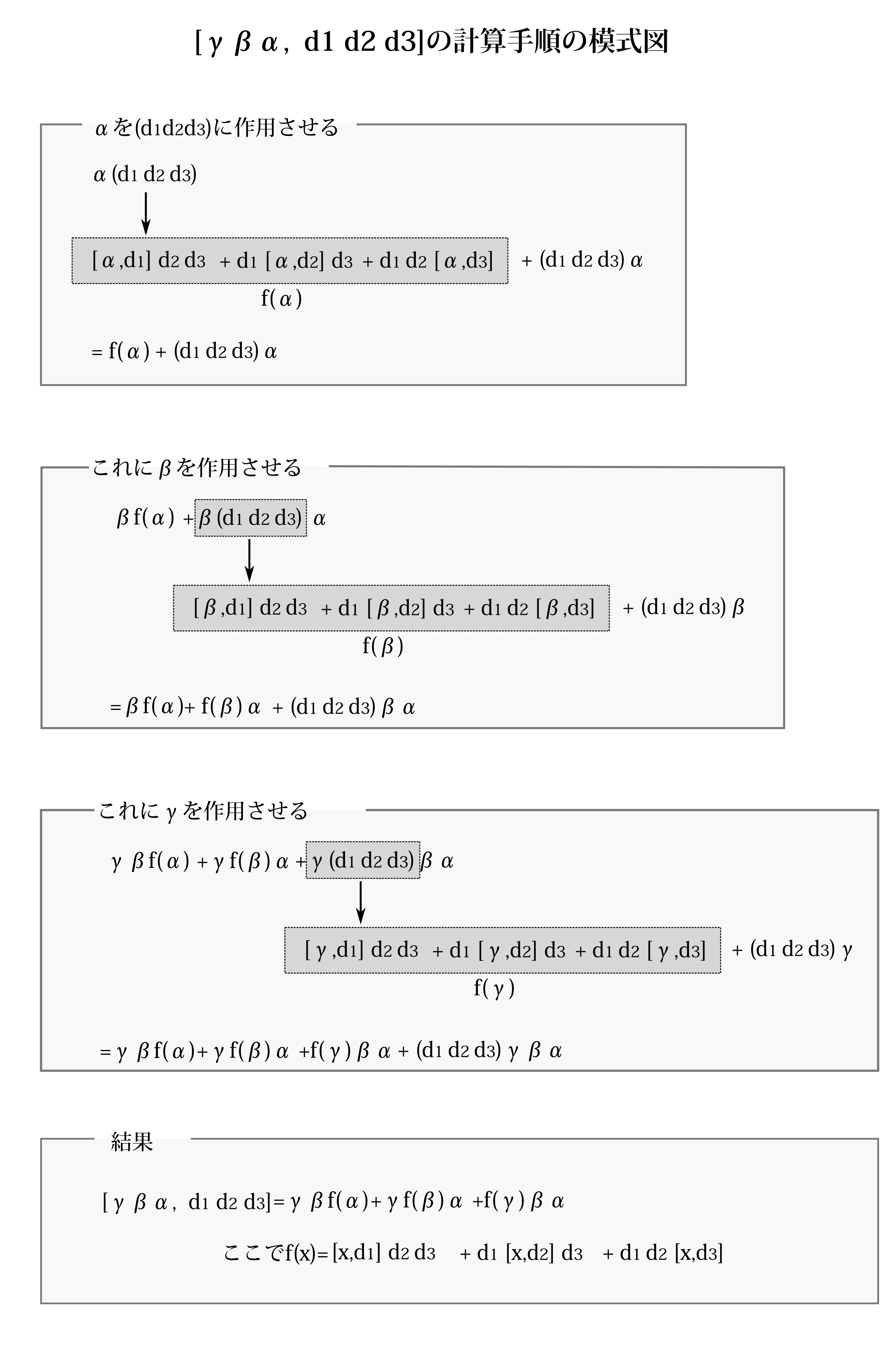
図5.1
ので参照して欲しい。さてすでに述べたように\(f(c_i)\)というのは\(c_i\)と\(d_1,d_2,d_3\)の全てとの交換子を含み、それに掛かっている項は、その交換子に含まれていない項の和で構成されている。だから(\ref{kouk})は\(c_i\)と\(d_j\)とのすべての交換子を含み、それに掛かっている項は\(c_i,d_j\)以外の全てである。今は\(C\)も\(D\)も3項づつでの話だったが、このことは項が何項あっても明らかになりたつわけで、一般に
補題D \(C=c_1c_2\cdots c_m\)、\(D=d_1d_2\cdots d_n\)のとき \[ [C,D]=\sum_{i,j}\Big([c_i,d_j]\times (c_i,d_jを除いた項をある順序で配置したものの積)\Big) \]
となる。ちなみにここでの証明の本筋には関係ないが残りの項の順序も書いておくと \[ [C,D]=\sum_{i,j}c_1\cdots c_{i-1}\Big(d_1\cdots d_{j-1}[c_i,d_j]d_{j+1}\cdots d_n\Big)c_{i+1}\cdots c_{m} \]である。
各項での一致
補題Cと補題Dを見比べれば、後は
補題E \(c\)と\(d\)が、\(p\)か位置\(x\)の関数の場合、\(\frac{1}{i\hbar}[c,d]\)は\(\{c,d\}\)を演算子に置き換えたものになる。
ことを示せれば補題Bが成り立つことになる。 この場合、\([c,d]\)が0でない ためには少なくともどちらかが\(p\)でなければならない(注 もちろん\(c\)も\(d\)も\(p\)なら0となってしまうが。少なくともということである。)。そのことに注意すれば \[ [c,d]= \left\{ \begin{array}{l} \displaystyle{-i\hbar\frac{\partial\, d}{\partial\, x_l}\qquad (c=p_lのとき、l=1,2,3,\cdots)}\\ \displaystyle{\quad i\hbar \frac{\partial\, c}{\partial\, x_l}\qquad (d=p_lのとき、l=1,2,3,\cdots)}\\ \displaystyle{\qquad 0\qquad\qquad (それ以外)} \end{array} \right. \] となることがわかる。
一方ポアソンの括弧は \[ \{c,d\}=\sum_k\left(\frac{\partial\, c}{\partial\, x_k}\frac{\partial\, d}{\partial\, p_k}-\frac{\partial\, c}{\partial\, p_k}\frac{\partial\, d}{\partial\, x_k}\right) \] であるが、この場合も\(\{c,d\}\)が0でないためには少なくとも\(c\)か\(d\)のどちらかが\(p\)でなければならない。そのことに注意すれば \[ \{c,d\}= \left\{ \begin{array}{l} \displaystyle{-\frac{\partial\, d}{\partial\, x_l}\qquad (c=p_lのとき、l=1,2,3,\cdots)}\\ \displaystyle{\quad \frac{\partial\, c}{\partial\, x_l}\qquad (d=p_lのとき、l=1,2,3,\cdots)}\\ \displaystyle{\qquad 0\qquad\qquad (それ以外)} \end{array} \right. \] となることがわかる。 よって補題Eが成り立つ。そして補題C、補題Dから補題Bが成り立つことになり、補題Aが成り立つというわけである。結果、任意の物理量の運動方程式は古典論でも量子論でも同じ項で構成される。これが今まで常に古典論と形式上の一致があった理由である。 しかし、だからと言って、平均値の運動が古典論の方程式に従うというわけではない。従うのは一般には、力の場の変化が波束内で小さいときだと思う。ここで証明したことをまとめると
命題5.3 物理量\(B\)の量子論での平均値の時間発展方程式と古典論での時間発展方程式は、それぞれ \[ \frac{d\left\langle B\right\rangle }{dt}=\psi^\dagger\left(\frac{1}{i\hbar}[B,H]+\frac{\partial\, B}{\partial\, t}\right)\psi \qquad\qquad\qquad \frac{dB}{dt}=\{B,H\}+\frac{\partial\, B}{\partial\, t} \] であるが、\(B\)と\(H\)が運動量\(p\)の多項式なら、この\(\{B,H\}+\frac{\partial\, B}{\partial\, t}\)を演算子に置き換えて、適切な順序に並べると\(\frac{1}{i\hbar}[B,H]+\frac{\partial\, B}{\partial\, t}\)に等しくなる。
角運動量の例
あまり必要ないかも知れないが、この命題の応用例を書いておこう。角運動量の\(z\)成分 \[ l_z=xp_y-yp_x \] を考える。系のハミルトニアンは \[ H=\sum_{i=1}^3\frac{p_i^2}{2m}+V \] とする。まず\(l_z\)の古典論での時間微分は \begin{eqnarray*} \frac{dl_z}{dt}&=&\frac{dx}{dt}p_y+x\frac{dp_y}{dt}-\frac{dy}{dt}p_x-y\frac{dp_x}{dt}\\ &=& \frac{p_x}{m}p_y+x\left(-\frac{\partial\, V}{\partial\, y}\right)-\frac{p_y}{m}p_x-y\left(-\frac{\partial\, V}{\partial\, x}\right)\\ &=& -x\frac{\partial\, V}{\partial\, y}+y\frac{\partial\, V}{\partial\, x} \end{eqnarray*} となる。一方量子論では\(\left\langle l_z\right\rangle \)の時間微分は、命題5.3より、\(\frac{1}{i\hbar}[l_z,H]\)を計算するまでもなく \[ \frac{d\left\langle l_z\right\rangle }{dt}=\psi^\dagger\left(-x\frac{\partial\, V}{\partial\, y}+y\frac{\partial\, V}{\partial\, x}\right)\psi \] になるはずである。\(x\cdot\frac{\partial\, V}{\partial\, y}=\frac{\partial\, V}{\partial\, y}\cdot x\)と順序によらないので、順序もこのままでいい。
さて、\(\left\langle l_z\right\rangle \)は、どういう場合に古典論の方程式に従って動くかと言うと、力の場――――ポテンシャルの空間微分――――の変化が波束内で十分小さく、力の場が波束の平均値での値としてよい場合である。 このときは、\(\mathbf{x}=(x,y,z)\)、\(F_x=-\partial\, V/\partial\, x\)、\(F_y=-\partial\, V/\partial\, y\)として \begin{eqnarray*} \frac{d\left\langle l_z\right\rangle }{dt}&=& \sum_{\mathbf{x}}\psi^*(\mathbf{x})\Big(xF_y(\mathbf{x})-yF_x(\mathbf{x})\Big)\psi(\mathbf{x})\\ &\cong& \left\langle x\right\rangle \cdot F_y\big(\left\langle \mathbf{x}\right\rangle \big)-\left\langle y\right\rangle F_x\big(\left\langle \mathbf{x}\right\rangle \big) \end{eqnarray*} となる。力の場が波束内で変化が十分小さい場合\(\left\langle x\right\rangle \)と\(\left\langle y\right\rangle \) の時間発展も古典論の方程式に従うので、角運動量の平均の時間発展も古典論の方程式に従うことになる。