第2章 変換行列と確率振幅の任意性(様々な表現)
この章では、変換行列と確率振幅には任意性があること、又、そのことと時間発展方程式との関係について述べる。 数学の話であり、物理の話はでてこない。この章での話は量子力学の体系の中ではやや脱線した話になっている。ただ、第3章での話――そこではスピンの変換行列と確率振幅を求める――の基礎にはなっている。
2.1節 任意性
すべての状態\(\lambda\)での確率分布の集まりを確率分布団と呼ぶことにする。与えられた確率分布団に対して、変換行列と確率振幅は一つに定まらず、任意性がある。この章ではそのことについて述べる。 物理量は何個あってもいいのだが、具体性を出すために、位置から運動量、それと位置からエネルギーの変換を考える。 位置から運動量への変換行列\(U_{px}\)、位置からエネルギーへの変換行列\(U_{\varepsilon x}\)、そして任意の状態\(\lambda\)での位置、運動量、エネルギーの確率振幅\(\psi(x;\lambda),\varphi(p;\lambda),\varphi(\varepsilon;\lambda)\)は与えられた状態\(\lambda\)での位置、運動量、エネルギーの確率分布\(P(x;\lambda),P(p;\lambda),P(\varepsilon;\lambda)\)に対して \begin{equation} P(x;\lambda)=|\psi(x;\lambda)|^2\qquad P(p;\lambda)=|\varphi(p;\lambda)|^2\qquad P(\varepsilon;\lambda)=|\varphi(\varepsilon;\lambda)|^2 \label{1a1} \end{equation} \begin{equation} \varphi(p;\lambda)=\sum_{x} U_{px}\psi(x;\lambda) \qquad \varphi(\varepsilon;\lambda)=\sum_x U_{\varepsilon x}\psi(x;\lambda) \label{1a2} \end{equation} を満たす。第1章 ではエネルギーの確率振幅は位置の確率振幅から定義したが、それはこの式を満たすためにはそうする必然性が――位相を除いて――あったからである。
位相の不定性
この確率振幅から新たに \begin{equation} \psi'(x;\lambda)\equiv e^{ig(x)}\psi(x;\lambda) \qquad \varphi'(p;\lambda)\equiv e^{if(p)}\varphi(p;\lambda) \qquad \varphi'(\varepsilon;\lambda)\equiv e^{ih(\varepsilon)}\varphi(\varepsilon;\lambda) \label{she} \end{equation} という確率振幅を作ろう。ここで\(f,g,h\)は状態に依存しない任意の実関数。そしてそれに合わせて新たな変換行列 \begin{equation} U'_{px}\equiv e^{if(p)}U_{px}e^{-ig(x)} \qquad U'_{\varepsilon x}\equiv e^{ih(\varepsilon)}U_{\varepsilon x}e^{-ig(x)} \label{henkan} \end{equation} を作ろう。この新たな確率振幅と変換行列は明らかに(\ref{1a1})、(\ref{1a2})を満たす。 変換(\ref{she})は線形変換であることに注意。 この確率振幅と変換行列の変換を視
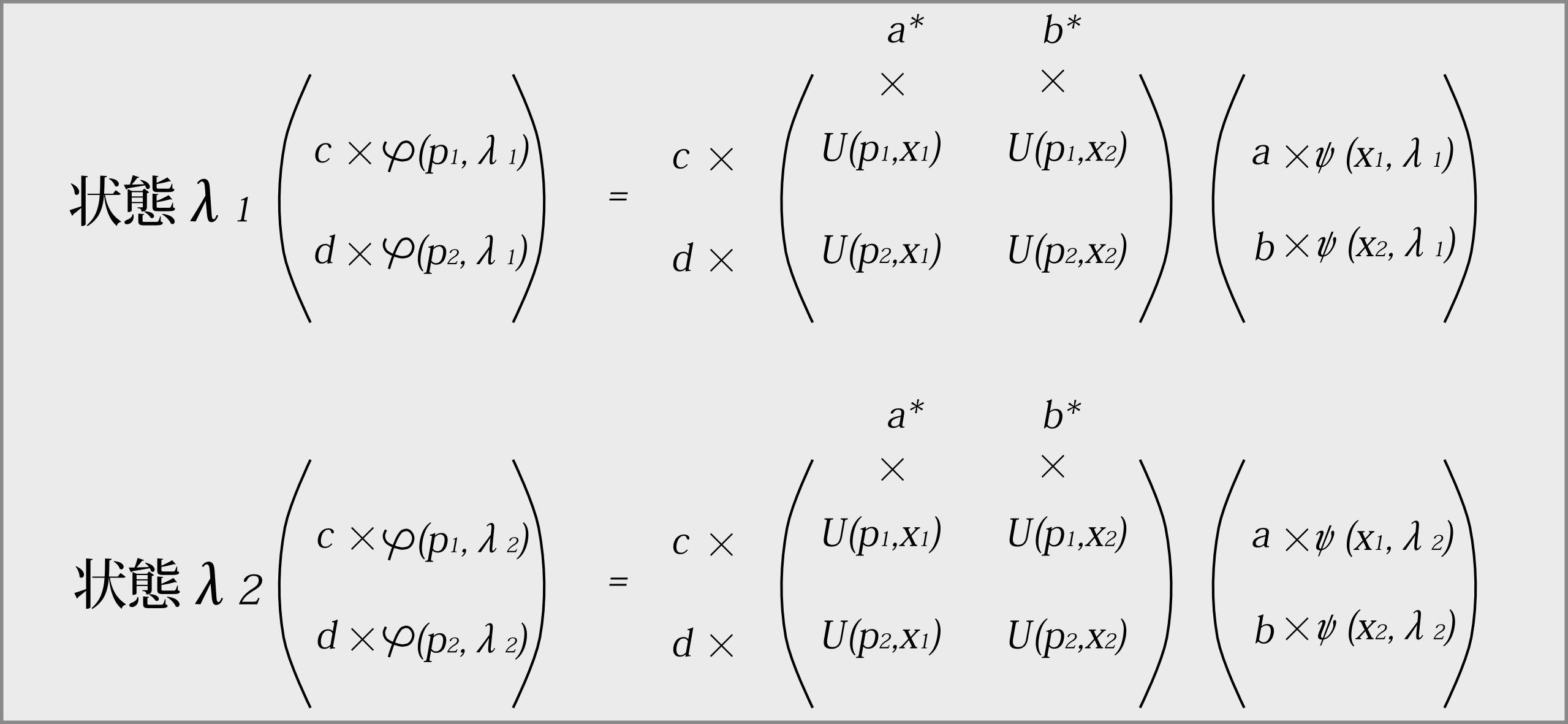
図2.1 \(|a|=|b|=|c|=|d|=1\)。\(\psi(x)\)の1行目に\(a\)を掛けたら\(U\)の1列目に\(a^*\)を掛ける。\(\varphi(p)\)の1行目に\(c\)を掛けたら\(U\)の1行目に\(c\)を掛ける。このような手順によってできる新たな変換行列、確率振幅も(\ref{1a1})、(\ref{1a2})を満たす。状態\(\lambda_1\)でも状態\(\lambda_2\)でも同じ操作が必要。
覚的に書くと図2.1のようになる。 この変換行列の変換(\ref{henkan})によってもユニタリー行列であることは変わらない。というのは、 ある列(又は行)のすべての成分に絶対値1の数を掛けても、各列間(又は各行間)の直交性は保たれるからである。 確率振幅に絶対値1の数を掛けるにあたって、成分や物理量によって値は変えてもいいが、すべての状態で同じ数を掛けなければならない。図2.1で言えば、状態\(\lambda_1\)で\(\psi(x_1,\lambda_1)\)に\(a\)を掛けたら、状態\(\lambda_2\)でも\(\psi(x_1,\lambda_2)\)に\(a\)を掛けなければならない。そうしなければ状態ごとに変換行列を変えなければならず、変換行列の意味をなさないからである。
定数倍の不定性
変換行列を定めても確率振幅には絶対値1の定数倍の不定性がある。つまり新しい確率振幅を \[ \psi'(x;\lambda)\equiv k(\lambda)\psi(x;\lambda) \qquad \varphi'(p;\lambda)\equiv k(\lambda)\varphi(p;\lambda) \qquad \varphi'(\varepsilon;\lambda)\equiv k(\lambda)\varphi(\varepsilon;\lambda) \label{hent} \] として変換行列はそのままで、(\ref{1a1})、(\ref{1a2})は満たされる。ここで\(k(\lambda)\)は絶対値1の複素数で、状態\(\lambda\)によって値を変えてもいいが、すべての物理量とすべての成分に同じものを掛けなければならない(図2.2)。 \(k(\lambda)\)がすべての状態で同じ値なら、これは(\ref{she})の特別な場合であり線形変換だが、そうでない場合は 、変換(\ref{she})の特別な場合ではなく線形変換ではない。(\ref{she})はすべての状態で同じ数を掛けなければならないからである。

図2.2 確率振幅の定数倍の不定性。\(|a|=|b|=1\)。確率振幅には同じ変換行列に対して定数倍の任意性がある。同じ状態ではすべての成分、すべての物理量で同じ数を掛けなければならない。
複素共役
また、明らかに 与えられた確率分布団に対して確率振幅\(\varphi(p;\lambda),\psi(x;\lambda),\varphi(\varepsilon;\lambda)\)、変換行列\(U_{px},U_{\varepsilon x}\)が式(\ref{1a1})、(\ref{1a2})を満たすなら、その複素共役\(\varphi^*(p;\lambda),\psi^*(x;\lambda),\varphi^*(\varepsilon;\lambda),U^*_{px},U^*_{\varepsilon x}\)も式(\ref{1a1})、(\ref{1a2})を満たす。 これは線形変換ではない。というのは、例えば、ある状態の確率振幅の複素共役は \[ \frac{1}{\sqrt{2}} \left(\begin{array}{c} 1-i\\ 0 \end{array}\right) \stackrel{i倍}{\longrightarrow} \frac{1}{\sqrt{2}} \left(\begin{array}{c} 1+i\\ 0 \end{array}\right) \] と変化し、これは\(i\)倍されているが、別の状態の確率振幅では \[ \left(\begin{array}{c} i\\ 0 \end{array}\right) \stackrel{-1倍}{\longrightarrow} \left(\begin{array}{c} -i\\ 0 \end{array}\right) \] というように、\(i\)倍ではなく、\(-1\)倍されているからである。なぜ線形か線形でないかにこだわるのかと言うと、後で述べる時間発展方程式と関係があるからである。
2.2節 確率振幅、変換行列は2つのグループに分かれること
確率振幅と変換行列にはこのように任意性があり、無限にあるのだが、与えられた確率分布団に対し解はどれくらいあるのだろうか。そこで、位置と運動量についての方程式 \begin{equation} P(x;\lambda)=|\psi(x;\lambda)|^2\qquad P(p;\lambda)=|\varphi(p;\lambda)|^2 \qquad\qquad \varphi(p;\lambda)=\sum_{x} U_{px}\psi(x;\lambda) \label{kaiga} \end{equation} の解はどれだけあるのかを考えよう。他の物理量に関しては、第第1章 で述べたように、位置(又は運動量)の確率振幅から自動的に決まってしまうのでとりあえず位置と運動量だけ考えればよい。 命題1.3で述べたように、変換行列の絶対値に関しては \[ |U_{px}|^2=P(p;x) \] が成り立つ。だからその絶対値は確率分布から定まるし、確率振幅の絶対値も確率分布から定まる。数式で書くと \[ |U_{px}|=\sqrt{P(p;x)}\qquad |\psi(x;\lambda)|=\sqrt{P(x;\lambda)}\qquad |\varphi(p;\lambda)|=\sqrt{P(p;\lambda)} \] ということである。そういうわけで、変換行列と確率振幅の位相だけが未知数ということになる。
さて、もし、(\ref{kaiga})の解が存在するなら、その解である変換行列\(U_{px}\)に \[ e^{if(p)}U_{px}e^{-ig(x)} \] という変換を何回か行えば、1行目と1列目を――元々行列には順序の概念がないので、これは1行目とか1列目でなくても何行目でも、何列目でもいいのだが――正の実数にすることができる。又、定数倍を掛けることによって\(\psi(x;\lambda)\)の1行目を正の実数にすることができる。 だから\(U_{px}\)の1行目と1列目、\(\psi(x;\lambda)\)の1行目は正の実数であるという条件のもと、解を探せば良い。 そういうわけで、変換行列\(U_{px}\)の2行目と2列目以降の位相、それ

図2.3
と確率振幅\(\psi(x;\lambda)\)の2行目以降の位相が未知数となる(図2.3参照)。 後はこの未知数を使って表した\(\sum_xU_{px}\psi(x;\lambda)\) が \begin{equation} P(p;\lambda)=\left|\sum_xU_{px}\psi(x;\lambda)\right|^2 \label{a118} \end{equation} を任意の状態\(\lambda\)で満たすように決めてやればよいわけである。状態は無限にあるのだから、この方程式は無限にあるということである。その無限個の方程式を、(測定変数を有限個に離散化しているとして)有限個の未知数で満たすものがあるというのは不思議な話である。 具体的にどう解を求めるかと言うと、それは煩雑なだけなので述べないが、例えば、状態\(\lambda\)として、\(\psi(x;\lambda)\)が2つの成分でのみ値が0とならないようなものを選んで方程式を作り、位相を決めていけばいいと思う。そしてこのように――1行目を正の実数にするなどの――制限をした上での変換行列の解はどれだけあるかと言うと、私の感触ではおそらく、2つしかないと思う。それは互いに複素共役なものが2つあるということである。もしそれが正しいならば、(\ref{kaiga})の解は今まで述べた変換で移り合えるものに限られるということである。つまり任意の2つの解\(U_{px},V_{px}\)があるとすると、\(U_{px}\)に\(e^{if(p)}U_{px}e^{-ig(x)}\)という変換を施したり、複素共役を取るなどすると\(V_{px}\)に移ることができるということである。このことは、変換行列は図2.4のように互いに複素共役なグループに別れ、それ以外の解は存在しないということを意味する。
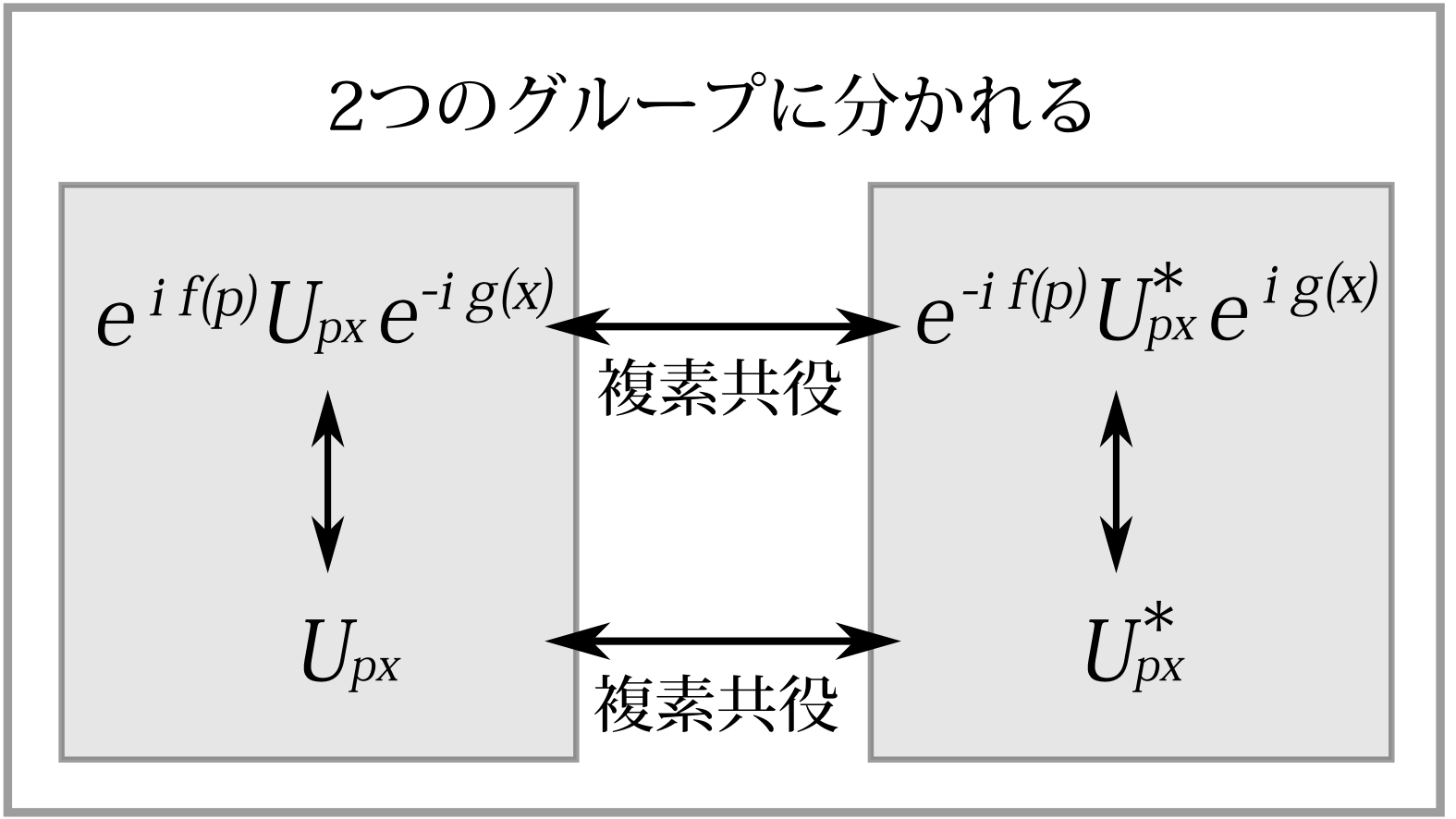
図2.4 変換行列は互いに複素共役な2つのグループに分かれると考えられる。
変換行列を1つ定めれば、状態\(\lambda\)に対して確率振幅は――定数倍を除いて――1つに定まると思う。その理由はこうである。状態\(\lambda\)での確率振幅を求めるということは(\ref{a118})式を解くということである。今、測定変数\(x\)も\(p\)も\(n\)個に離散化されているとすると方程式は\(p\)を離散化した分の\(n\)個あることになる。一方未知数は\(\psi(x;\lambda)\)の2行目以降の位相の未知数\(n-1\)個である(図2.5)。これでは合わないが、変換行列がユニタリーなので、確率の全事象
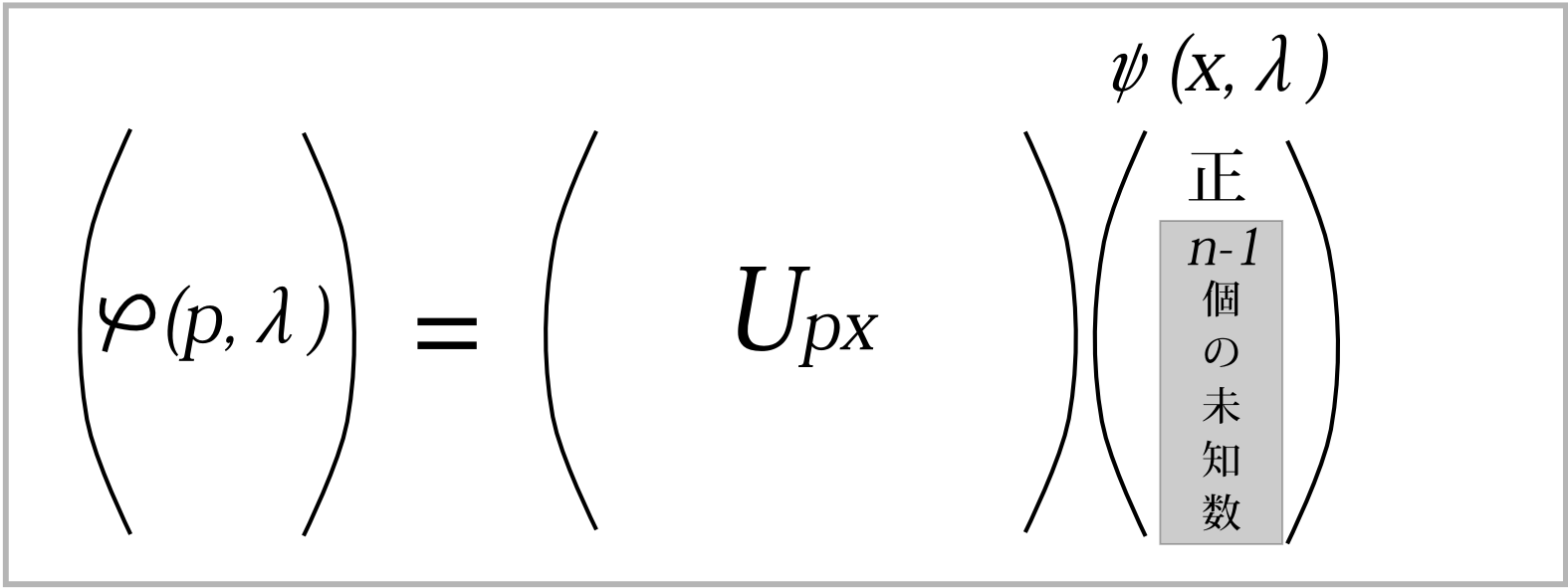
図2.5
が1に自動的に規格化される。すなわち \[ \sum_p\left|\sum_xU_{px}\psi(x;\lambda)\right|^2=1 \] が自動的に成り立つので方程式の数は1つ減り\(n-1\)個になる。\(n-1\)個の未知数で\(n-1\)個の方程式なら通常は解は1つに定まるだろう。実際はその複素共役も必ず解になるので2つであろう。これが解が2つのみと考える理由である。今の話は証明にも何にもなっていないが、ここらへんはあまり物理とは関係ない話なので、おそらく2つであろうということでいいと思う。もしこれ以外の解があったら物理的にどういうことを意味するのかという疑問の方が強い。 次の第3章でスピン1/2の系で実際に確率振幅と変換行列を求めるが、少なくともその系ではこれらのことは成り立っている。 尚、位置と運動量以外に関する変換行列や確率振幅は、第1章でのべたように位置の(又は運動量の)確率振幅から自動的に決まっていくので――私自身、詳細までは詰めてないが――同様に2つのグループに分かれることになる。
2.3節 ここまでのまとめと考察
ここで、今までのことを模式図を使ってイメージを描いておこう。 考えている系で――電子1つの系だとか、電子と陽子の系だとか、ポテンシャルがクーロンポテンシャルだとかという意味での系――許される変換行列の組\(U_{\varepsilon x},U_{px},\cdots\)、そして同じグループ内の組、\(U'_{\varepsilon x},U'_{px},\cdots\)、\(U''_{\varepsilon x},U''_{px},\cdots\)、・・・・・が無限にあり(図2.6)、この変換行列に対応
図2.6 その系に許される変換行列の組
して、状態ごとに物理量ごとの確率振幅がある(図2.7)。図2.7の状態\(\lambda_1\)で変換行列\(U\)の組(グレイの部分)を詳しく見ると、図2.8のように確率振幅には絶対値が1の定数倍の不定性がある。そして最後にこの裏返しのような形で、これらの複素共役も許される変換行列と確率振幅である。

図2.7 状態ごとに変換行列に対応した確率振幅がある
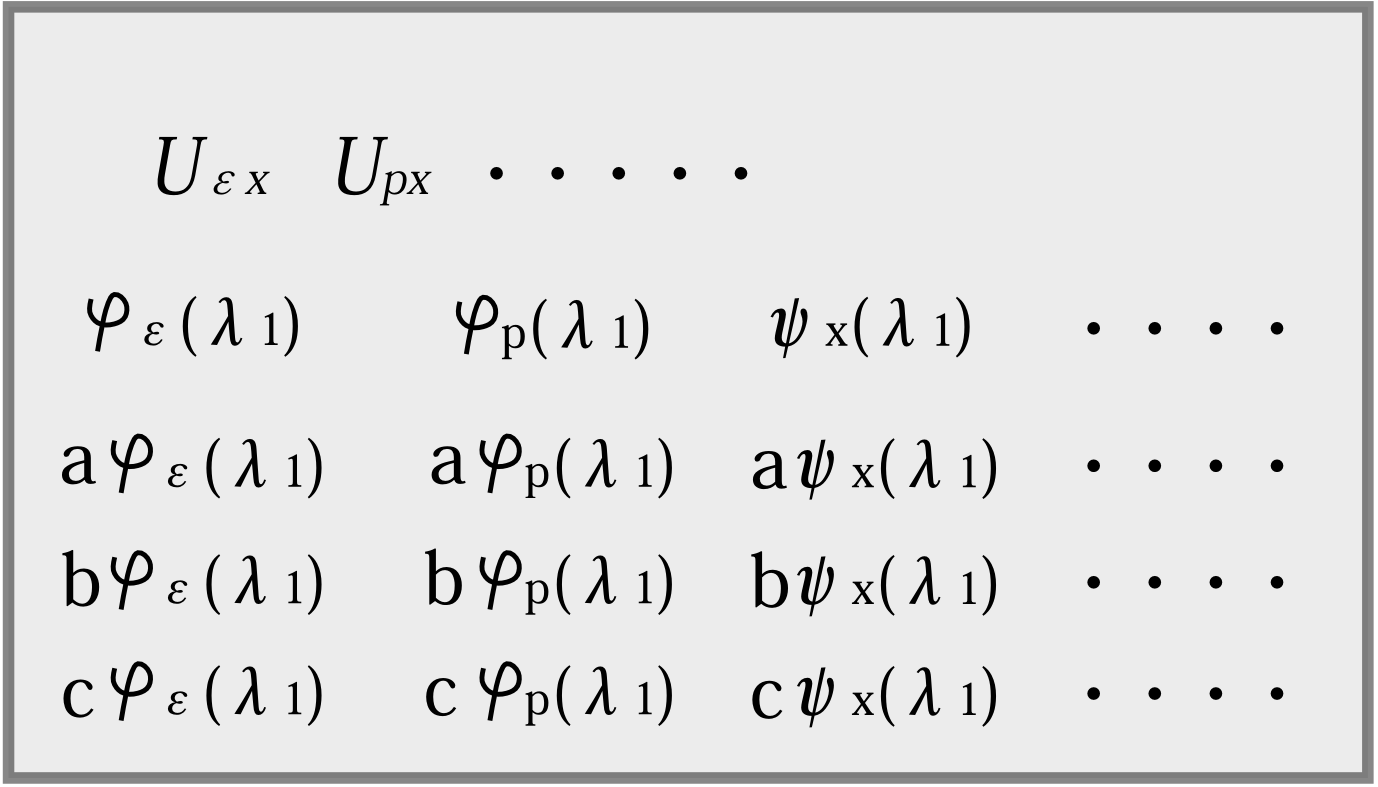
図2.8 図2.7のグレイの部分の詳細。\(|a|=|b|=|c|=1\)。変換行列を定めても確率振幅には定数倍の不定性がある。
確率振幅に任意性があることについては、線形代数学の考え方に沿えば、表示\(\varphi_\varepsilon\)が\(\varphi'_\varepsilon=e^{ih(\varepsilon)}\varphi_\varepsilon\)に変わるというのは基底が変わるからだということになる。つまり\(\varphi_\varepsilon\)の基底が\(\mathbf{e}_\varepsilon\)だとすると、\(\varphi'_\varepsilon\)の基底は\(\mathbf{e}'_\varepsilon =e^{-ih(\varepsilon)}\mathbf{e}_\varepsilon\)に変わったからだと言える。ところがこの\(\mathbf{e}_\varepsilon\)も\(\mathbf{e}'_\varepsilon\)も同じ量子力学的状態を指すのである。こういうことはベクトル空間では起きないことである。状態は決して線形代数学で言うベクトル空間ではないのである。ここらへんはややこしいところではあるが、確率振幅は単に確率分布を計算するための便宜と見て、無理に数学的にすっきりした言葉で説明しようなどと考えなくてもいいのではと思う。 私としてはそれよりも物理法則としての量子力学を理解したいとう熱意のほうがある。
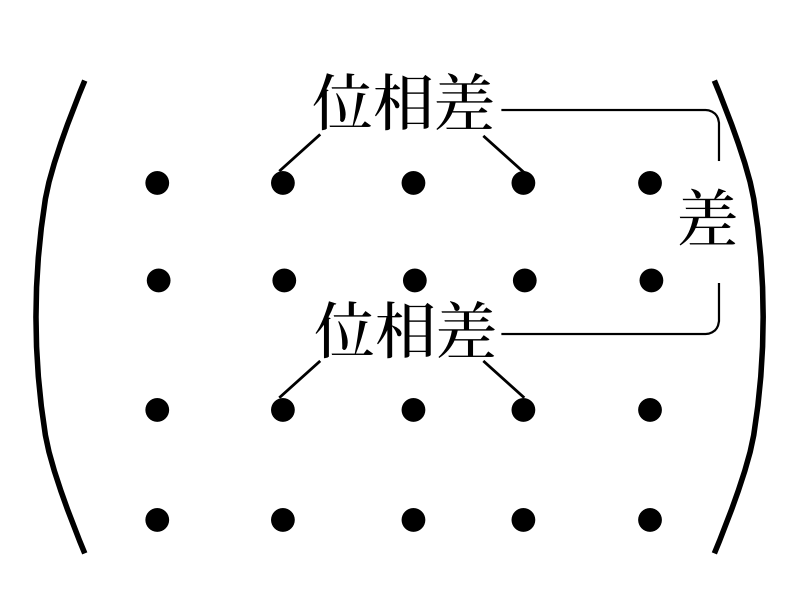
図2.9
変換行列と確率振幅に任意性がある中で、物理的に意味があるものは何かというと、変換行列では――成分の絶対値は言うまでもないが――同じ行のある列と別の列の成分の位相差と、他の行でのその列とその別の列の成分の位相差の差である。例えば1行目で2列目と4列目の位相差 \[ \arg \big[U(1,2)\big]-\arg \big[U(1,4)\big] \] と3行目の2列目と4列目の位相差 \[ \arg \big[U(3,2)\big]-\arg \big[U(3,4)\big] \] の差が不変量となり物理的な意味を持つ(図2.9)。これは同じグループ内での変換行列は、同じ行に同じ位相を加えること、同じ列に同じ位相を加えることで移り合うものだからである。もっと一般的に書けば \[ \Big(\arg \big[U(\alpha,\beta)\big]-\arg \big[U(\alpha,\gamma)\big]\Big)-\Big(\arg \big[U(\alpha',\beta)\big]-\arg \big[U(\alpha',\gamma)\big]\Big) \] が――正確には複素共役の場合もあるので、この絶対値が――不変量になる。それゆえ、1行目と1列目を正の実数と定めれば――これは位相をすべて0にすることを意味する――2行目、2列目以降の位相は意味を持つ。 今の議論は行を列、列を行と読み替えても成り立つ。
又、変換行列を定めると、状態に対応する確率振幅も定まるわけだが、確率振幅で意味があるのは――その絶対値はもちろんであるが――2つの成分間の位相差 \[ \arg \big[\psi_x\big]-\arg\big[\psi_{x'}\big] \] である。それゆえ、1行目を正の実数と定めてしまえば2行目以降の位相は意味を持つ。
又、変換行列と確率振幅の積\(U_{px}\psi_x\)での不変量は――絶対値は言うまでもないが――\(x\)を変化させたときの位相差 \[ \arg\big[U_{px}\psi_x\big]-\arg\big[U_{px'}\psi_{x'}\big] \] である。 このように変換行列にしろ確率振幅にしろ、その位相というのはどこかに基準を定めて意味を持つものであり、それ自身には意味はない。
2.4節 時間発展方程式と2つのグループの関係
今まで、変換行列と確率振幅には任意性があること、そして互いに複素共役 な2つのグループに分かれることを述べてきた。この節では、そのことと時間発展方程式との関係について述べる。ここでの話も数学だけであり、物理は出てこない。第1.8節で述べたようにエネルギー表示の時間発展方程式は \[ i\hbar\frac{d\varphi_\varepsilon}{dt}=\sum_{\varepsilon'}H_{\varepsilon\varepsilon'}\varphi_{\varepsilon'}\qquad\qquad H_{\varepsilon\varepsilon'}=\delta_{\varepsilon\varepsilon'}\varepsilon'\qquad\qquad \text{(エネルギー表示)} \] であった。他の表示、例えば位置、運動量などは、第1.8節で述べたように、変換行列を使って表示の変更をすればよいのであって \[ i\hbar\frac{d\psi_{x}}{dt}=\sum_{x'}H_{xx'}\psi_{x'}\qquad\qquad H_{xx'}=\sum_\varepsilon U^*_{\varepsilon x}\;\varepsilon\; U_{\varepsilon x'}\qquad\qquad \text{(位置表示)} \] \[ i\hbar\frac{d\varphi_{p}}{dt}=\sum_{p'}H_{pp'}\varphi_{p'}\qquad\qquad H_{pp'}=\sum_\varepsilon U^*_{\varepsilon p}\;\varepsilon\; U_{\varepsilon p'}\qquad\qquad \text{(運動量表示)} \] となるのであった。さて、この系の許される変換行列の組\(U_{\varepsilon x},U_{px},\cdots\)は――この「\(\cdots\)」は位置、エネルギー、運動量以外の変換行列などその他という意味――無数にあるわけで、以下のような疑問が生じる。まず、この無数にある変換行列の組から1つの組を定める。そうすると、与えられた任意の初期状態に対して、確率振幅は――定数倍を除いて――1つに定まる。それを上記方程式に従って時間発展させる。 次に、別の変換行列の組み合わせを選んで、この同じ初期状態に対応する確率振幅を定め、この方程式によって時間発展させる。このとき、この2つは同じ状態変化をするのだろうか。という疑問である。答えを先に言うと、同じグループ内の変換行列の組では同じ時間発展するが、異なるグループでの変換行列の組では時間は逆行する。そのことについて今から説明する。
同じグループ内
今、時刻\(t=0\)で状態を\(\lambda(0)\)としよう。そして変換行列の組を1つ選び、それを \[ U_{\varepsilon x},U_{px},\cdots \] とする。すると この状態\(\lambda(0)\)に対応する確率振幅の組が定まり、それを \[ \varphi_\varepsilon(0),\psi_x(0),\varphi_p(0),\cdots \] としよう。そしてこの初期状態から上記の方程式に従って時間発展させたときの時刻\(t\)での解を \[ \varphi_\varepsilon(t),\psi_x(t),\varphi_p(t),\cdots \] としよう。そしてそれに対応する状態を\(\lambda(t)\)としよう。 この組み合わせと同じグループにある別の変換行列の組 \[ U'_{\varepsilon x}=e^{ih(\varepsilon)}U_{\varepsilon x}e^{-ig(x)},\qquad \qquad U'_{px}=e^{if(p)}U_{px}e^{-ig(x)},\qquad\qquad\cdots\cdots \] を考えよう。そして、この変換行列に合わせて、確率振幅の組 \[ \varphi'_\varepsilon(t)= e^{ih(\varepsilon)}\varphi_\varepsilon(t),\qquad \psi'_x(t)=e^{ig(x)}\psi_x(t),\qquad \varphi'_p(t)=e^{if(p)}\varphi_p(t),\qquad \cdots\cdots \] を考えよう。 このダッシュ組の確率振幅は当たり前だが、時刻\(t\)で状態は\(\lambda(t)\)を表すことになる。というのは、状態とは確率分布の組のことであり、確率分布が各時刻でダッシュ無しの方と同じだからである。
さて、このダッシュ組の確率振幅はどういう時間発展方程式を満たすのだろうか。エネルギーに関してはダッシュ無しの\(\varphi_\varepsilon(t)\)は \[ i\hbar\frac{d\varphi_\varepsilon(t)}{dt}=\varepsilon\varphi_\varepsilon(t) \] を満たしているのだから、\(\varphi_\varepsilon(t)=e^{-ih(\varepsilon)}\varphi'_\varepsilon(t)\)をこれに代入すると、ダッシュ有りの方も \begin{equation} i\hbar\frac{d\varphi'_\varepsilon(t)}{dt}=\varepsilon\varphi'_\varepsilon(t) \label{302} \end{equation} 満たすことになり、全く同じ形となる。位置や運動量などはどうなるかというと、第1.8節で述べたのと同様にこの線形方程式(\ref{302})を位置表示や運動量表示に変換してやればよいわけで、位置表示の方は \[ i\hbar \frac{d \psi'_x(t)}{dt}=\sum_{x'}H'_{xx'}\psi'_{x'}(t)\qquad\qquad H'_{xx'}=\sum_\varepsilon\left(U'_{\varepsilon x}\right)^*\varepsilon \;U'_{\varepsilon x'} \] であり、運動量に関しても同様である。位置や運動量ではハミルトニアンの部分がダッシュ付きの、つまりこの組自身の変換行列を使わなければならない。だからエネルギー以外の方程式は形式は同じでも中身は異なる方程式であることには注意すべきである。 さて以上の議論から言えることは、
命題2.1 無数にある変換行列の組から同じグループの中のどの組を選んでも、与えられた初期条件から時間発展方程式 \[ i\hbar\frac{d\varphi_\varepsilon}{dt}=\sum_{\varepsilon'}H_{\varepsilon\varepsilon'}\varphi_{\varepsilon'}\qquad\qquad H_{\varepsilon\varepsilon'}=\delta_{\varepsilon\varepsilon'}\varepsilon'\qquad\qquad \text{(エネルギー表示)} \] \[ i\hbar\frac{d\psi_{x}}{dt}=\sum_{x'}H_{xx'}\psi_{x'}\qquad\qquad H_{xx'}=\sum_\varepsilon U^*_{\varepsilon x}\;\varepsilon\; U_{\varepsilon x'}\qquad\text{(位置表示)} \] 等 に従って――ここに現れる変換行列はその組の変換行列を使わなければならない――時間発展させると、同じ状態に刻々と変化する。
ということである。尚、同じ組の中だけでなく、同じグループ内の確率振幅はすべて線形変換の関係にあり、微分方程式の表示の変更の関係にある。例えば、ダッシュ無しのエネルギー表示の方程式とダッシュ有りの位置表示の方程式も一種の微分方程式の表示の変更である。
異なるグループ間
さて、次に異なるグループの組み合わせを選ぼう。つまり元の \[ \varphi_\varepsilon(t),\psi_x(t),\varphi_p(t),\cdots ,U_{\varepsilon x},U_{px},\cdots \] の複素共役 \[ \varphi^*_\varepsilon(t),\psi^*_x(t),\varphi^*_p(t),\cdots ,U^*_{\varepsilon x},U^*_{px},\cdots \] を考えるということである。 この確率振幅の時刻\(t\)での状態も明らかに\(\lambda(t)\)を表すことになる。ではどういう時間発展方程式を満たすのだろうか。 元のエネルギーの確率振幅は \[ i\hbar \frac{d \varphi_\varepsilon(t)}{dt}=\varepsilon\varphi_\varepsilon(t) \] を満たすので、この複素共役をとると \[ -i\hbar \frac{d \varphi^*_\varepsilon(t)}{dt}=\varepsilon\varphi^*_\varepsilon(t) \] となる。つまり\(\varphi^*_\varepsilon(t)\)は \[ -i\hbar \frac{d f_\varepsilon}{dt}=\varepsilon f_\varepsilon \] という微分方程式を満たすことになる。異なるグループ間の確率振幅は線形変換で結ばれていないので、単なる微分方程式の表示の変更にはならず、方程式自身が変わることになる。
さて、2つの微分方程式 \[ i\hbar \frac{d f_\varepsilon}{dt}=\varepsilon f_\varepsilon \qquad と \qquad -i\hbar \frac{d f_\varepsilon}{dt}=\varepsilon f_\varepsilon \] では、もし\(f_\varepsilon(t)\)が左の解なら、\(f_\varepsilon(-t)\)が右の解になる。つまりこの2つの方程式の解は互いに時間を逆行する。 だから\(t=0\)で\(\varphi^*_\varepsilon(0)\)を初期条件として \[ i\hbar \frac{d f_\varepsilon}{dt}=\varepsilon f_\varepsilon \] の方の方程式で時間発展させたら、状態は時刻\(t\)で――変換行列が定まっていれば、状態はエネルギーの確率振幅だけで定まることに注意――\(\lambda(-t)\)となる。そして、命題2.1より、こちらのグループのどの変換行列の組を使っても、状態は\(\lambda(-t)\)と時間変化する。さて、現実の世界では初期状態が定まれば、その後は一意的に定まる。ということは現実の状態の時間発展に合うのはどちらか一方のグループの変換行列の組ということになる。合わない方は \[ -i\hbar \frac{d f_\varepsilon}{dt}=\varepsilon f_\varepsilon \] の方を使えば合う。 今までは――エネルギーの確率振幅のみで状態は定まるので――エネルギーの確率振幅だけの話をしてきたが、位置や運動量などの確率振幅\(\psi_x^*(t),\varphi_p^*(t)\)の時間発展方程式は、今まで同様、エネルギーの方程式から変換すればいいだけの話である。エネルギーの確率振幅\(\varphi_\varepsilon^*(t)\)の方程式がそれぞれ \[ -i\hbar \frac{d\varphi^*_\varepsilon(t)}{dt}=\varepsilon \varphi^*_\varepsilon(t)\qquad\qquad i\hbar \frac{d\varphi^*_\varepsilon(t)}{dt}=\varepsilon \varphi^*_\varepsilon(t) \] を満たすなら、例えば位置に関してはそれぞれ \[ -i\hbar \frac{d \psi^*_x(t)}{dt}=\sum_{x'}H^*_{xx'}\psi^*_{x'}(t)\qquad\qquad i\hbar \frac{d \psi^*_x(t)}{dt}=\sum_{x'}H^*_{xx'}\psi^*_{x'}(t) \] になるだけの話である。ハミルトニアンは \[ H^*_{xx'}=\sum_\varepsilon\left(U^*_{\varepsilon x}\right)^*\varepsilon \; U_{\varepsilon x'}^* \] となる。この\(H^*_{xx'}\)は元のハミルトニアンの複素共役という意味でこう書いたが、ハミルトニアンの作り方自体は元のハミルトニアンの作り方と全く同じである。つまり元の\(U_{\varepsilon x}\)の部分がこの組の変換行列である\(U^*_{\varepsilon x}\)で置き換き変わったものになっている。 以上の議論をまとめると次のようになる。
命題2.2 異なるグループから任意の変換行列の組を1つづつ選んで、与えられた初期状態から方程式 \[ i\hbar\frac{d\varphi_\varepsilon}{dt}=\sum_{\varepsilon'}H_{\varepsilon\varepsilon'}\varphi_{\varepsilon'}\qquad\qquad H_{\varepsilon\varepsilon'}=\delta_{\varepsilon\varepsilon'}\varepsilon'\qquad\qquad \text{(エネルギー表示)} \] \[ i\hbar\frac{d\psi_{x}}{dt}=\sum_{x'}H_{xx'}\psi_{x'}\qquad\qquad H_{xx'}=\sum_\varepsilon U^*_{\varepsilon x}\;\varepsilon\; U_{\varepsilon x'}\qquad \text{(位置表示)} \] 等に従って時間発展させると、状態の時間変化は互いに逆行する。現実に合うのはどちらかのグループとなる。合わない方は\(-i\hbar \frac{d f_\varepsilon}{dt}=\varepsilon f_\varepsilon\) の方を使えば現実に合う。尚、ここに現れる変換行列はその組の変換行列であることに注意。
運動量から位置への変換行列は\(e^{ipx/\hbar}\)だが、これは時間発展方程式として\(i\hbar \frac{d f_\varepsilon}{dt}=\varepsilon f_\varepsilon\)を使っているからである。もし\(-i\hbar \frac{d f_\varepsilon}{dt}=\varepsilon f_\varepsilon\)の方を使うなら変換行列は\(e^{-ipx/\hbar}\)となる。