付録C スピン磁気モーメントを持つ粒子が磁場中で2つに分かれること
第7章で電荷を持つスピン1/2の粒子は不均一磁場中で、波束がスピンの向きに応じて2つに分離すると述べたが、この付録では、そのことが量子力学の時間発展方程式で現実に起こりうることを示す。 粒子の軌道グループでは位置\(\mathbf{x}\)、スピングループでは\(z\)方向表示でのハミルトニアン\(H\)は付録Bで述べたように、CGSガウス単位系で \[ H=\frac{1}{2m}\sum_{i=1}^{i=3}\left(\frac{\hbar}{i}\frac{\partial\,}{\partial\, x_i}-A_i\right)^2-\frac{q}{mc}\left(B_x S^x_{z'z}+B_y S^y_{z'z}+B_z S^z_{z'z}\right) \] だと考えられる。ここで\(A_i\)はベクトルポテンシャル、\(q\)は電荷、\(m\)は質量、\(c\)は光速、\(B_x,B_y,B_z\)は磁場のそれぞれの成分。ベクトルポテンシャルはローレンツ力に関わる項であり、今はスピンによる上下の分離を考えたいのでベクトルポテンシャルは無視しよう。するとハミルトニアンは \[ H=\frac{\hbar^2}{2m}\triangle-\frac{q}{mc}\left(B_x S^x_{z'z}+B_y S^y_{z'z}+B_z S^z_{z'z}\right) \] となる。位置\(\mathbf{x}\)、スピングループでは\(z\)方向表示での確率振幅\(\psi(\mathbf{x},z)\)の時間発展方程式は \begin{equation} i\hbar \frac{d \psi(\mathbf{x},z)}{dt}=\frac{\hbar^2}{2m}\triangle\psi(\mathbf{x},z)-\sum_{x,z}\frac{q}{mc}\left(B_x S^x_{z'z}+B_y S^y_{z'z}+B_z S^z_{z'z}\right)\psi(\mathbf{x},z) \label{w2} \end{equation} となる。\(\psi(\mathbf{x},z)\)の測定変数\(z\)はスピンの上下に応じてそれぞれ\(+\)と\(-\)をとるとする。 この方程式で\(\psi(\mathbf{x},+)\)と\(\psi(\mathbf{x},-)\)の波束がそれぞれ上下に分離するかを見てみたい。しないなら、この方程式は現実に合わないということで正しくないのである。
スピン演算子の\(z\)方向の表示は、付録Aで述べたように \[ S^x_{z'z}=\frac{1}{2}\hbar \left( \begin{array}{cc} 0&1\\ 1&0 \end{array} \right) \qquad S^y_{z'z}=\frac{1}{2}\hbar \left( \begin{array}{cc} 0&-i\\ i&0 \end{array} \right) \quad S^z_{z'z}=\frac{1}{2}\hbar \left( \begin{array}{cc} 1&0\\ 0&-1 \end{array} \right) \] である。 だから \[ B_x S^x_{z'z}+B_y S^y_{z'z}+B_z S^z_{z'z}=\frac{1}{2}\hbar \left( \begin{array}{cc} B_z&B_x-iB_y\\ B_x+iB_y&-B_z \end{array} \right) \] となる。これを使うと時間発展方程式(\ref{w2})は、\(\psi(\mathbf{x},+),\psi(\mathbf{x},-)\)をそれぞれ\(\psi_+(\mathbf{x}),\psi_-(\mathbf{x})\)と書き換えて、 \[ i\hbar \frac{d}{dt} \left(\begin{array}{c} \psi_+(\mathbf{x})\\ \psi_-(\mathbf{x}) \end{array}\right) = -\frac{\hbar^2}{2m}\triangle \left(\begin{array}{c} \psi_+(\mathbf{x})\\ \psi_-(\mathbf{x}) \end{array}\right) -\frac{q\hbar}{2mc} \left( \begin{array}{cc} B_z&B_x-iB_y\\ B_x+iB_y&-B_z \end{array} \right) \left(\begin{array}{c} \psi_+(\mathbf{x})\\ \psi_-(\mathbf{x}) \end{array}\right) \] となる。これを展開すると \[ i\hbar \frac{d}{dt}\psi_+(\mathbf{x})=-\frac{\hbar^2}{2m}\triangle \psi_+(\mathbf{x})-\frac{q\hbar}{2mc}\Big[B_z\psi_+(\mathbf{x})+(B_x-iB_y)\psi_-(\mathbf{x})\Big] \] \[ i\hbar \frac{d}{dt}\psi_-(\mathbf{x})=-\frac{\hbar^2}{2m}\triangle \psi_-(\mathbf{x})-\frac{q\hbar}{2mc}\Big[-B_z\psi_-(\mathbf{x})+(B_x+iB_y)\psi_+(\mathbf{x})\Big] \] となる。今、磁場は図C.1のように\(z\)軸の正の向きに向いていおり、上に行
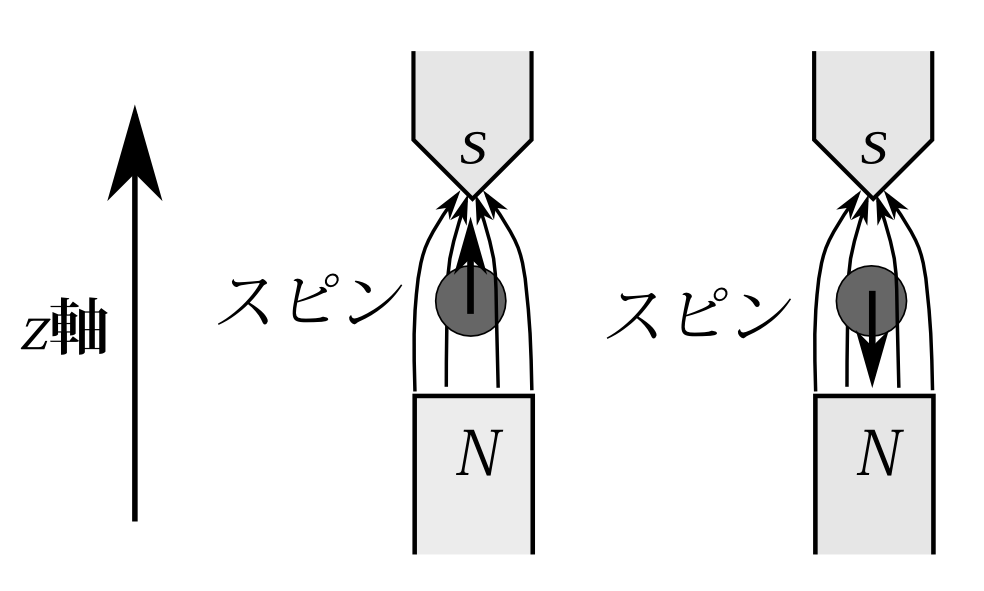
図C.1
くほど磁場は強くなっているとしよう。そして横方向の磁場\(B_x\)と\(B_y\)は縦方向の磁場\(B_z\)に比べて十分小さいとしよう。とは言っても\(B_x,B_y\)が小さすぎると\(B_z\)は上向き平行になってしまい、磁場は一定になってしまう。小さすぎてもだめなのだが、とにかく横方向の磁場は無視できるとしよう。すると時間発展方程式は \[ i\hbar \frac{d}{dt}\psi_+(\mathbf{x})=-\frac{\hbar^2}{2m}\triangle \psi_+(\mathbf{x})-\frac{q\hbar}{2mc}B_z\psi_+(\mathbf{x}) \] \[ i\hbar \frac{d}{dt}\psi_-(\mathbf{x})=-\frac{\hbar^2}{2m}\triangle \psi_-(\mathbf{x})+\frac{q\hbar}{2mc}B_z\psi_-(\mathbf{x}) \] となる。 さて第4章の式(8)で述べたように、位置の確率振幅が方程式 \[ i\hbar\frac{d\psi}{dt}=-\frac{\hbar^2}{2m}\triangle \psi +V\psi \] を満たすとき 波束の平均の位置\(\left\langle x\right\rangle \)は \[ \frac{d^2\left\langle x_i\right\rangle }{dt^2}=-\left\langle \frac{\partial\, V}{\partial\, x_i}\right\rangle \] を満たすのであった。それを今の方程式に適用すると、それぞれ\(-\frac{q\hbar}{2mc}B_z,\frac{q\hbar}{2mc}B_z\) がポテンシャル\(V\)の役割を演じているのだから、 \(\psi_+,\psi_-\)の波束の\(z\)成分の平均\(\left\langle z\right\rangle _+,\left\langle z\right\rangle _-\)は \[ \frac{d^2\left\langle z\right\rangle _+}{dt^2}=\frac{q\hbar}{2mc}\left\langle \frac{\partial\, B_z}{\partial\, z}\right\rangle \]\[ \frac{d^2\left\langle z\right\rangle _-}{dt^2}=-\frac{q\hbar}{2mc}\left\langle \frac{\partial\, B_z}{\partial\, z}\right\rangle \] を満たすことになる。今\(\frac{\partial\, B_z}{\partial\, z}>0\)としているのだから、\(q>0\)とすると、\(\left\langle z\right\rangle _+\)は上に加速し、\(\left\langle z\right\rangle _-\)は下に加速するということである。波束もおおむね平均値の運動に従うと考えれば、スピンの向きに応じで上下に分離するということである。 やや粗っぽい議論だったが、波束がスピンの向きによって上下に分離することは十分ありうるということはわかったと思う。そしてシュテルンーゲルラッハの実験が示しているように、実際に上下に分離するのだから、この方程式は現実を――――非常に大雑把にだが――――説明することができるわけで、この方程式の正しさの根拠になるということである。