第4章　固有ベクトル法―固有ベクトルと変換行列

　この章では固有ベクトルの方法を使って、変換行列を求める。尚、固有ベクトル法というのは私が勝手にそう呼んでいるだけで、世間ではこんな名称は通用しない、正準量子化法といわれているのかもしれないが、正準量子化法というのは単に演算子の設定の仕方に対する呼び方だと思うので、概念的に違う感じがする。もともとの定義では変換行列は確率分布の関数として求められるべきものであった。しかし、自然界に存在する確率分布を見つけ出すのは困難なので、この方法で変換行列を推測しようというわけである。この方法で変換行列を求めることによって量子力学の体系は完成する。ただスピンにはこの方法は通用しない。まず変換行列の求める手続きを述べたあと、この方法によって求めた変換行列を使えば、物理量の平均値が古典力学を再現することを述べる。

4.1節　演算子

　今から述べる演算子というのは確率振幅に作用させる演算子のことである。確率振幅に作用させて、別の量子力学的状態へ写像するのかといえば、 そんなことはなく、単に固有ベクトルと固有値を求めるための便宜である。

　直交座標で考え、位置座標の\(x_i\)成分の演算子とそれに対応する運動量の\(p_i\)成分の演算子を定義する。直交座標としたのは、曲線座標だとうまくいかないからである。今は1粒子に話を限定しない。\(x_i\)成分の演算子を\(\hat{x}_i\)と書こう。又\(p_i\)成分の演算子を\(\hat{p}_i\)と書こう。 \(\hat{x}_i,\hat{p_i}\)は 位置の確率振幅\(\psi(x)\)に作用させると \begin{equation} \begin{array}{llll} \text{位置}\qquad&\hat{x}_i \psi(x)\equiv x_i \psi(x)\qquad\qquad \text{運動量}\qquad&\hat{p}_i\psi(x)\equiv \displaystyle{\frac{\hbar}{i}\frac{\partial\,}{\partial\, x_i}\psi(x)} \end{array} \label{f1} \end{equation} となるように定義する。これは演算子の位置表示であり、運動量や他の物理量の確率振幅に作用させるときは、演算子の表示はそれに応じて変化する。

　他の物理量の演算子については、その物理量を位置と運動量の関数で表わし、その位置と運動量を今定義した演算子で置き換えるという方法で決める。例えばエネルギーなら、位置と運動量で \[ \sum_i\frac{p_i^2}{2m_i}+V(x) \] と表される。ここの位置と運動量を(\ref{f1})で定義したもので置き換えると、エネルギー演算子は \begin{equation} \sum_i\frac{1}{2m_i}\left(\frac{\hbar}{i}\frac{\partial\,}{\partial\, x_i}\right)^2+V(x) \label{f2} \end{equation} となるわけである。ただ磁場のある場合はこの形ではなく、古典力学のハミルトニアンは、ベクトルポテンシャル\(A_i(x)\)、スカラーポテンシャル\(\phi(x)\)、\(q\)を電荷、\(c\)を光速、CGSガウス単位系として、 \[ \frac{1}{2m}\sum_{i=1}^3\left(p_i-\frac{q}{c}A_i(x)\right)^2+q\phi(x) \] である。これは1粒子の場合である。2粒子以上の場合は記号が煩雑になるので、この論文では、この形のハミルトニアンに関しては1粒子の場合だけ扱う。 この場合のエネルギー演算子は \begin{equation} \frac{1}{2m}\sum_{i=1}^3\left(\frac{\hbar}{i}\frac{\partial\,}{\partial\, x_i}-\frac{q}{c}A_i(x)\right)^2+q\phi(x) \label{jibano} \end{equation} となる。

　角運動量の\(x\)成分\(l_x\)なら、古典力学では \[ l_x=y\;p_z-z\;p_y \] と表されるので、この位置と運動量を(\ref{f1})で定義したもので置き換えると \[ y\cdot\left(\frac{\hbar}{i}\frac{\partial\,}{\partial\, z}\right)-z\cdot\left(\frac{\hbar}{i}\frac{\partial\,}{\partial\, y}\right) \] となるわけである。 置き換える際に演算子の順序に注意しなければならない。角運動量の\(x\)成分の２乗\(l_x^2\)は \[ (y\;p_z-z\;p_y)(y\;p_z-z\;p_y)=y p_z y p_z -y p_z z p_y -z p_y y p_z +z p_y z p_y \] である。ここで、例えば\(y p_z z p_y\)の項は古典力学では\(yzp_zp_y\)でも同じだが、演算子にすると掛ける順序によって結果が異なる。ではどういう順序が正しいのかというと、それには決まった規則はない。ただ単に実験的に正しい変換行列となる順序が正しいとしかいいようがない。\(l_x^2\)に関して言えば最初の\((y\;p_z-z\;p_y)(y\;p_z-z\;p_y)\)の段階で演算子に置き換えるとうまくいくようである。

4.2節　固有ベクトル

　さて、この演算子を使っていかにして変換行列を求めるかというと、簡単に言えばこの演算子に含まれる変数の固有関数がこの物理量からその変数への変換行列になるというだけである。そして測定値は固有値となる値しか現れない。尚、関数はベクトルの一種なのでより一般的な言葉として「固有ベクトル法」としたのである。これだけでは何のことかわからないと思うので、具体例で説明していこう。

運動量

　まず、運動量から説明する。運動量の\(p_i\)成分から位置の\(x_i\)成分への変換行列を求める。運動量\(p_i\)成分の演算子は\(x_i\)しか含んでいないのでその固有関数は\(x_i\)のみの関数である。 運動量演算子\(\frac{\hbar}{i}\frac{\partial\,}{\partial\, x_i}\)の固有値\(p_i\)である規格化した固有関数\(k(x_i;p_i)\)が運動量の値\(p_i\)の確率振幅から、位置の値\(x_i\)の確率振幅への変換成分となる。尚、運動量演算子の固有値\(p_i\)の固有関数は規格化を除くと \[k(x_i;p_i)=\exp\left({\frac{i}{\hbar}x_i p_i}\right)\] である。変換行列はユニタリーでなければならないので、逆変換は\(k^*(x_i,p_i)\)である。 例えば1粒子系で\(p_x\)から\(x\)への変換は \[ \psi(x,p_y,p_z)=\sum_{p_x}k(x;p_x)\cdot\varphi(p_x,p_y,p_z) \] となる。これを\(y,z\)成分でも繰り返すと \[ \psi(x,y,z)=\sum_{p_x,p_y,p_z}\Big[k(x;p_x)\cdot k(y;p_y)\cdot k(z;p_z)\Big]\cdot\varphi(p_x,p_y,p_z) \] となる。\(k(x;p_x)\cdot k(y;p_y)\cdot k(z;p_z)\)が運動量\(p_x,p_y,p_z\)から位置\(x,y,z\)への変換行列である。

角運動量

　次に角運動量の場合について説明しよう。角運動量の\(z\)成分の演算子\(\hat{l}_z\)は \[ \hat{l}_z=x\cdot\left(\frac{\hbar}{i}\frac{\partial\,}{\partial\, y}\right)-y\cdot\left(\frac{\hbar}{i}\frac{\partial\,}{\partial\, x}\right) \] であるが、これは極座標\(r,\theta,\phi\)で表すと、計算は省くが、 \[\frac{\hbar}{i}\frac{\partial\,}{\partial\, \phi} \] となる。この演算子は\(\phi\)しか含んでいないので固有関数は\(\phi\)のみの関数である。この演算子の固有値\(l_z\)のときの固有関数\(k(\phi;l_z)\)は \[ k(\phi;l_z)=\exp\left(\frac{i l_z\phi}{\hbar}\right) \] となる。経度\(\phi\)が一回転して、\(2\pi\)増えても連続であるためには、固有値\(l_z\)は\(\hbar\)の整数倍でなければならない。そしてその測定値はこの固有値しか現れない。\(\hat{l}_z\)が\(\phi\)しか含んでいないので、\(l_z\)は\(\phi\)とのみ変換する。\(l_z\)から\(\phi\)への変換は、規格化を無視すると、 \[ \psi(r,\theta,\phi)=\sum_{l_z}k(\phi;l_z)\varphi(r,\theta,l_z) \] と変換される。角運動量の2乗の演算子は、極座標\(r,\theta,\phi\)で表すと、計算は省くが、 \[ \hat{l}_x^2+\hat{l}_y^2+\hat{l}_z^2=-\hbar^2\left[\frac{1}{\sin\theta}\frac{\partial\,}{\partial\, \theta}\left(\sin\theta\frac{\partial\,}{\partial\,\theta}\right)+\frac{1}{\sin^2\theta}\frac{\partial\,^2}{\partial\, \phi^2}\right] \] となる。この演算子は\(\theta\)、\(\phi\)しか含まないので固有関数は\(\theta,\phi\)のみの関数である。だから角運動量の２乗の固有値\(\kappa\)の固有関数\(k(\theta,\phi;\; \kappa)\)は\(\kappa\)から\(\theta,\phi\)への変換行列となる。この固有関数は縮退――同じ固有値\(\kappa\)でもいくつかの独立した関数があること――しており、球面調和関数\(Y^m_l(\theta,\phi)\)として知られている。ここで指標\(l\)は\(\kappa\)と \[ \hbar^2 l(l+1)=\kappa\qquad l=0,1,2,3\cdots \] という関係にある。又、指標\(m\)は角運動量の\(z\)成分\(l_z\)と \[ m\hbar=l_z\qquad\qquad m=0,\pm 1,\pm2,\cdots \qquad |m|\le l \] という関係にある。角運動量の絶対値の2乗が同じでも角運動量の\(z\)成分が異なると固有関数が異なることになる。 詳しくはほとんどの量子力学の教科書にでている。そして\(\kappa,l_z\)から\(\theta,\phi\)への変換は \[ \psi(r,\theta,\phi)=\sum_{\kappa,l_z}Y^m_l(\theta,\phi)\varphi(r,\kappa,l_z) \] という変換になる。

エネルギー

　最後にエネルギーについて説明しよう。エネルギー演算子はすでに述べたように(\ref{f2})式や(\ref{jibano})式であるが、再掲すると \[ -\sum_i\frac{\hbar^2}{2m_i}\frac{\partial\,^2}{\partial\, x_i^2}+V(x)\qquad\qquad \frac{1}{2m}\sum_{i=1}^3\left(\frac{\hbar}{i}\frac{\partial\,}{\partial\, x_i}-\frac{q}{c}A_i(x)\right)^2+q\phi(x) \] である。これは位置変数\(x_i\)すべてを含んでいるので、固有値\(\varepsilon\)での固有関数\(k(x;\varepsilon)\)がエネルギー表示から位置\(x\)表示への変換行列となる。1.8節で述べたように、変換行列が決まれば位置表示のハミルトニアン\(H_{xx'}\)が決まるということであり、位置の確率振幅の時間発展方程式が決まる。それは \[ i\hbar \frac{d\psi_x}{dt}= \sum_{x'}H_{xx'}\psi_{x'} \qquad\qquad H_{xx'}=\sum_\varepsilon k(x;\varepsilon)\cdot\varepsilon\cdot k^*(x';\varepsilon) \] である。 ところで、このハミルトニアンとエネルギー演算子に関して以下の命題が成り立つ。

命題4.1　エネルギー演算子は位置表示のハミルトニアン\(H_{xx'}\)に等しい。つまり \begin{equation} -\sum_i\frac{\hbar^2}{2m_i}\frac{\partial\,^2}{\partial\, x_i^2}+V(x)=\sum_\varepsilon k(x;\varepsilon)\cdot\varepsilon\cdot k^*(x';\varepsilon)\qquad\text{（磁場のない場合）} \label{129a} \end{equation} \[ \frac{1}{2m}\sum_{i=1}^3\left(\frac{\hbar}{i}\frac{\partial\,}{\partial\, x_i}-\frac{q}{c}A_i(x)\right)^2+q\phi(x)=\sum_\varepsilon k(x;\varepsilon)\cdot\varepsilon\cdot k^*(x';\varepsilon)\qquad\text{（磁場のある場合）} \] である。

その理由というのは、これは線形代数学の復習なのだが、(\ref{129a})の左辺というのは位置の確率振幅に作用しているのだから、エネルギー演算子の位置表示だと言える。 エネルギー表示にするには \begin{equation} \sum_x k^*(x;\varepsilon)\left(-\sum_i\frac{\hbar^2}{2m_i}\frac{\partial\,^2}{\partial\, x_i^2}+V(x)\right)k(x;\varepsilon') \label{rinji} \end{equation} とすればよい。\(k(x;\varepsilon)\)は固有関数なのだから \[ \left(-\sum_i\frac{\hbar^2}{2m_i}\frac{\partial\,^2}{\partial\, x_i^2}+V(x)\right)k(x;\varepsilon') =\varepsilon'k(x;\varepsilon') \] である。だから(\ref{rinji})は \[ \sum_x k^*(x;\varepsilon)\cdot\varepsilon'\cdot k(x;\varepsilon') \] となる。\(k(x;\varepsilon)\)はユニタリ―のはずだから \[ \sum_x k^*(x;\varepsilon)\cdot\varepsilon'\cdot k(x;\varepsilon') =\delta_{\varepsilon\varepsilon'}\varepsilon' \] となる。結局エネルギー演算子のエネルギー表示は \[ \sum_x k^*(x;\varepsilon)\left(-\sum_i\frac{\hbar^2}{2m_i}\frac{\partial\,^2}{\partial\, x_i^2}+V(x)\right)k(x;\varepsilon') =\delta_{\varepsilon\varepsilon'}\varepsilon' \] と対角成分が\(\varepsilon\)である対角行列になる。 一方(\ref{129a})の右辺というのは元々エネルギー表示で対角成分が\(\varepsilon\)である対角行列\(\delta_{\varepsilon\varepsilon'}\varepsilon'\)を位置表示に変換したものである。つまり、(\ref{129a})の左辺も右辺もエネルギー表示では対角成分が\(\varepsilon\)の対角行列だということである。だから当然、それを位置表示にしたものも等しいというわけである。そういうわけで位置表示の時間発展方程式は \[ i\hbar \frac{d\psi_x}{dt}=\left(-\sum_i\frac{\hbar^2}{2m_i}\frac{\partial\,^2}{\partial\, x_i^2}+V(x)\right) \psi_x \] となる。磁場のある場合の証明も全く同様である。尚、今はエネルギー演算子のエネルギー表示は、対角成分がエネルギー固有値である対角行列になることを示したが、この議論は他の物理量でも成り立つことで、一般に

命題4.2　物理量\(B\)の演算子の\(B\)表示は、対角成分が固有値\(b\)である対角行列\(\delta_{bb'}b'\)になる

と言える。

まとめ

　運動量についてはどんな系でも変換行列は\(e^{\frac{i}{\hbar}x\cdot p}\)であり、わざわざ演算子やら、固有値やら、そんなややこしいことを持ち出さなくても単に変換行列は\(e^{\frac{i}{\hbar}x\cdot p}\)だというだけの話である。角運動量も同様である。ただ、演算子を使うと、後で述べる古典論との対応を示すのには便利ではある。一方、エネルギーから位置への変換行列は系によって異なるので、今述べた方法はエネルギーから位置への変換行列を求めるのに極めて有効なのである。 今まで述べたこ固有ベクトル法というものを一般的に言い表すと以下のようになる。

物理量\(B\)の演算子は位置変数\(\alpha\)で表され、その固有値\(b\)のときの固有関数が\(k(\alpha;b)\)のとき、 つまり、 \[ \hat{B}\cdot k(\alpha;b)=b\cdot k(\alpha;b) \] のとき、 その\(k(\alpha;b)\)がその物理量\(B\)表示の値\(b\)から、位置表示の値\(\alpha\)への変換成分となる。逆変換は\(k^*(\alpha;b)\)である。又、物理量\(B\)を測定したときに現れる測定値はその固有値のみである。

4.3節　考察

　ところで、このような突飛な方法で求めた変換行列や離散的な測定値というものは正しく自然現象を表しているのだろうか。とりうる離散的な測定値が正しいかは直接測定して確かめればよい。間接的には統計力学のカノニカル分布を使って求めた結果が自然現象を正しく表しているかという方法でも調べられるだろう。一方変換行列の正しさを確認するには1.2節で述べた性質がこの変換行列で満たされるのかを、実験で求めた確率分布を用いて、確かめなければならない。これは以下のようなことを確認する必要があるということである。 今、位置と運動量のある確率分布を実験で求めたとする。それに対して、その絶対値の2乗がこの確率分布に等しく、かつ、 この固有ベクトル法で求めた位置と運動量の 変換行列で結ばれる位置と運動量の確率振幅が存在するのかを確かめなければならない。 又、このようにして求めたエネルギー測定状態での位置表示の確率振幅は、この固有ベクトル法の変換行列と等しいのか。さらにはこの変換行列で定義されるエネルギーの確率振幅の絶対値の2乗が実際の確率分布に等しくなってくれるか。他の物理量でもこれらのことを確かめなければならない。 しかしその肝心の確率分布自体を得る方法がほとんどない（1.10節参照）のである。だから結局は固有ベクトル法による変換行列の正しさは後（4.4節参照）で述べる間接的な方法で確かめられるだけなのである。

　このように固有ベクトル法で求めた変換行列の正しさを実験的に確認することは困難なのだが、これが正しいとすると、1.1節で述べた残された問題、以下に再掲するが、はスピンを除いてすべて答えが出たことになる。

1については、変換行列が決まればハミルトニアン行列が決まり、確率振幅の時間発展方程式が決まる。その絶対値の2乗が確率分布である。具体的には、すでに変換行列が定まっているので、初期状態（確率分布）から初期確率振幅を求めることができ、それを時間発展方程式で時間発展させ、その絶対値の2乗が知りたい確率分布ということになる。2については、 まず、与えられた位置と運動量の確率分布から確率振幅を求める。変換行列が定まっているのだからこれは可能なはずである。そしてこの確率振幅から変換行列を使って他の物理量の確率振幅を求め、その絶対値の2乗がその物理量の確率分布となる。こうやって位置と運動量の確率分布から他の物理量の確率分布が定まる。又、位置と運動量の確率分布の間に関係があることは、互いの確率振幅が変換行列で結ばれるというのだから自明であろう。 3については、測定した物理量は、確率振幅が測定値のみ0でないものに移るので、その確率振幅をこの変換行列を使って他の物理量の確率振幅に変換することによって、確率分布もわかることになる。4については、固有値が測定値ということで解決である。

　ところで、この固有ベクトル法では

という数学上の疑問が湧くが、このことは演算子がエルミート行列ならすべて満たされるのである。運動量と角運動量に関しては実際に変換行列は求まっており、それは満たされることはわかっている。有限次元のエルミート行列が以上の性質を持ていることは上級の線形代数の教科書に出ている。そしてここで出てくる、位置、運動量、角運動量、エネルギーの演算子は、すべてエルミート行列――ただ位置や、運動量などは連続変数なので行列という言葉はあまり適当ではないとはないのだが――である。エルミート行列と言っても無限次元なので無限次元のまま扱っては証明は難しいとは思う。しかし物理では何でも有限で止めていいのである。尚、これらがエルミート行列であることの証明は付録Dで示す。

　ところで、ここで求めた変換行列を使って測定状態を表すと、明らかにおかしな結論に導かれてしまう。そのことを簡単に述べよう。位置を測ると位置の測定状態に飛び移る。 \(x,y,z\)の\(x\)成分を測って、値が\(x'\)だったとすると、\(x\)成分に関する確率振幅は\(\psi_x=\delta_{xx'}\)に飛び移る。これを運動量の\(p_x\)成分に変換すると、 \begin{eqnarray*} \varphi_{p_x}&=&\sum_x \exp\left(-ip_x x/\hbar\right)\delta_{xx'}\\ &=&\exp(-ip_x x'/\hbar) \end{eqnarray*} になる。ということは運動量の\(p_x\)成分は\(-\infty\)から\(+\infty\)まで等しい確率分布になるということである。そして運動エネルギーの期待値は無限大になる。そんなおかしなことはない。

　又、運動量の\(p_x\)成分を測ったとして、値が\(p'_x\)だったとする。状態は\(p'_x\)の測定状態に飛び移り、その運動量表示の確率振幅は\(\delta_{p_xp'_x}\)である。これを位置\(x\)成分のの確率振幅に変換すると \begin{eqnarray*} \psi_x&=&\sum_{p_x} \exp\left(ip_x x/\hbar\right)\delta_{p_xp'_x}\\ &=&\exp(ip'_x x/\hbar) \end{eqnarray*} になる。\(x\)成分の確率分布は\(-\infty\)から\(+\infty\)まで等しくなる。 これもどう考えてもおかしいわけである。粒子の運動量を地球上で測ったら、その直後にその粒子は、アンドロメダ星雲にある確率も地球にある確率も等しくなるのである。これは粒子が地球から存在しなくなるのと同じである。もちろん、運動量の測定も幅がある。だからそんなに波束は広がらないというのも事実である。しかし精度をどんどん上げていけば、いずれこういう結論に達してしまうのである。

4.4節　固有ベクトル法による変換行列はなぜよいか

　さて、すでに述べたように、この固有ベクトル法で求められる変換行列が自然を正しく表しているかを直接実験で確かめるのは困難である。 一方、変換行列が定まるということは確率振幅の時間発展方程式が定まるということである。この時間発展方程式が自然を正しく表しているということを示せれば、この変換行列の正しさの有力な根拠になる。それを実験で確かめるということが一番いいに決まっているが、実験上の困難が多々あることであろう。それで、ここでは古典力学との対比で考えたい。古典力学の運動方程式は長年にわたって正しいと思われてきたし、多くの場合近似的には正しいわけである。だから量子力学によって古典力学の運動方程式を導けなければならないはずである。それはこの変換行列を使えば、ある意味導けるのである。それを今から説明しよう。

　量子論の測定結果というのは確率的にしか言えないのだが、その測定値の平均値というものが考えられる。例えば位置のある一つの成分\(x_i\)の平均\(\left\langle x_i\right \rangle\)なら、\(\langle\quad\rangle\)は平均を意味するとするが、 \[ \left\langle x_i\right\rangle =\sum_{x} x_i|\psi(x)|^2 \] であるし、運動量\(p_i\)成分の平均\(\left\langle p_i\right\rangle \)なら \[ \left\langle p_i\right\rangle =\sum_p p_i|\varphi(p)|^2 \] である。ここで和はこの確率振幅のすべての測定変数で取るとする。他の物理量でも同様である。さて、固有ベクトル法で変換行列が決まるわけだが、変換行列が決まれば確率振幅の時間発展も決まり、平均値の時間発展も決まる。その平均値の時間発展が古典力学の正準方程式に一致するのである。つまり \begin{equation} m_i\frac{d\left\langle x_i\right\rangle }{dt}=\left\langle p_i\right\rangle \label{g1} \end{equation} \begin{equation} \frac{d\left\langle p_i\right\rangle }{dt}=-\left\langle \frac{\partial\, V}{\partial\, x_i}\right\rangle \label{g2} \end{equation} が成り立つ。 この式(\ref{g1})、(\ref{g2})の証明は第5章に回す。

　(\ref{g1})をもう１回時間で微分すると \[ m_i\frac{d^2\left\langle x_i\right\rangle }{dt}=\frac{d\left\langle p_i\right\rangle }{dt} \] となり、これと(\ref{g2})より \begin{equation} m_i\frac{d^2\left\langle x_i\right\rangle }{dt}=-\left\langle \frac{\partial\, V}{\partial\, x_i}\right\rangle \label{g3} \end{equation} も成り立つ。

図4.1　1次元自由粒子での量子論での位置\(x\)と運動量\(p\)の確率分布の時間発展(左図)と古典論での粒子の時間発展(右図)。縦軸が時間\(t\)。

　例えば１次元の自由粒子で考えてみよう。初期確率分布として位置の平均値は０、運動量の平均値は正とする。確率分布は図4.1の左図ような時間発展をすると考えられる。運動量の平均は変化しない。位置の平均は一定の速度で増加する。確率分布の広がり自体はどうなるかわからないので想像で描いた。位置を測定すると図4.1のように縦に無限に伸びた分布になり、運動量を測定すると横に無限に伸びた分布になる。これは前節(4.3節)でも述べたようにおかいしのである。

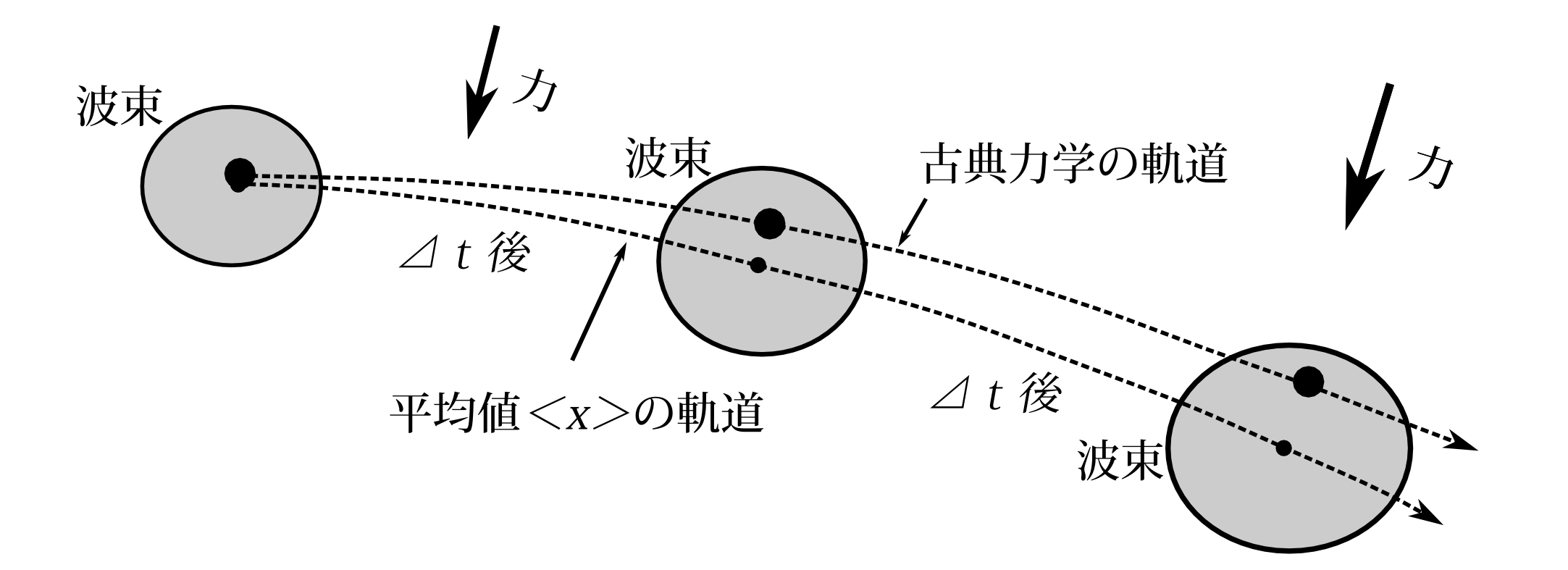
図4.2　位置の平均値\(\left\langle x\right\rangle \)の運動は決して古典力学に従うわけではない。しかし波束内での力の場が一定とみなしていいなら、平均値の運動は古典力学に従う。

　さて、位置の確率分布のことを波束と呼ぶことにしよう。又、力の場を \[ F_i(x)\equiv-\frac{\partial\, V(x)}{\partial\, x_i} \] と書くことにしよう。 (\ref{g3})が主張していることというのは、位置の平均値の加速度の質量倍\(m_i\frac{d^2\left\langle x_i\right\rangle }{dt^2}\)が、力の場 のこの波束中での平均、つまり \[ \sum_xF_i(x)|\psi(x)|^2 \] に等しいということである。 決して位置の平均値の場所\(\left\langle x\right\rangle \)での力 \( F_i\big(\left\langle x\right\rangle \big) \) と等しいわけではない。つまり、位置の平均値\(\left\langle x\right\rangle \)は決して古典力学の方程式に従って動くわけではないのである（図4.2）。 しかし、その波束の広がりが十分小さくて、力の場がその波束内で一定とみなしていいなら、 \begin{eqnarray*} \sum_xF_i(x)|\psi(x)|^2&\simeq &F_i\big(\left\langle x\right\rangle \big)\sum_x|\psi(x)|^2\\ &=&F_i\big(\left\langle x\right\rangle \big) \end{eqnarray*} となり、 位置の平均値の加速度の質量倍はその平均値で の場所\(\left\langle x\right\rangle \)での力の場と一致するわけである。この場合位置の平均値\(\left\langle x\right\rangle \)は古典力学の方程式に従って動く。 以上まとめると

波束が十分小さくて、力の場\(F_i(x)\)がその波束内で一定であるとみなしてよいなら、位置の平均値\(\left\langle x\right\rangle \)の運動は古典力学の運動方程式 \[ m_i\frac{d^2\left\langle x_i\right\rangle }{dt}=F_i\big(\left\langle x\right\rangle \big) \] に従う。

又、波束が十分小さいなら、位置の平均値\(\left\langle x\right\rangle \)と波束自体もおおむね一致しているので、波束自体の運動も古典力学の方程式に従うと言える。

4.5節　古典力学が再現されているか

　このように波束の運動は古典力学の式に概ね従うのだが、これでこの固有ベクトル法の正しさがわかったとせず、少し立ち止まって考えよう。(\ref{g1})、(\ref{g2})の意味はある状態\(\lambda\)というのを何度もセットして運動量を測る。又、同じようにその状態\(\lambda\)を何度もセットして位置を測る。そして運動量と位置の平均を計算する。 次に微小時間後に、状態\(\lambda\)は時間発展方程式に従って少し変化しているわけだが、その変化した状態で、同じように運動量と位置を測る。そして平均値を得る。そしてその平均値の時間微分を計算する。その結果(\ref{g1})、(\ref{g2})の等式が成り立つというのである。さらに、もう一つ微小時間後で測定すれば平均値の時間による２階微分が得られる。その結果(\ref{g3})が成り立つというわけである。だから、こう考えると古典力学を再現しているとは言い難いのである。

　しかし私は、確率分布自体が測定値そのものである と感じている。これは世間では明確には言われていないが、暗にそういう意味として使っている気がするのである。測定をすると幅があり、誤差があるが、その範囲に確率分布は収まるわけである。その範囲がその測定値の範囲でありかつ確率分布の範囲なのである。量子力学の出現以前に電子の電荷と質量の比を求めることができたのだが、それを求めるときに使った電子の軌道というのは確率分布の軌道だったのである。 しかしこれは測定とは何を意味するかをはっきりさせないと意味がないことではある。又、確率分布は他の粒子に影響を及ぼしている。1粒子の系でのポテンシャルというのは他の物体の確率分布からポテンシャルを近似的に導き出しているのである。 だから

確率分布というものは単なる測定時における確率というだけでなく、確率分布自体が外部に作用を及ぼしているのであり、それ自体が測定値なのである

と言った方がいいと思っている。そう考えれば、上に述べたように波束(位置の確率分布)はおおむね古典力学の方程式に動くのであるから、測定値が古典力学の方程式に従って動くということになり、古典力学を再現していると言える。又、 古典力学が今まで概ね正しい結果を出し続けてきたことにも納得がいくであろう。

PDFファイルA4、130ページ、4.8MB

目次

序文

記号・用語

第1章

第2章

第3章

第4章

第5章

第6章

第7章

第8章

第9章

第10章

付録A

付録B

付録C

付録D

付録E

おわりに

Copyright All rights reserved