第6章 位置の測定
6.1節 測定とは、位置、長さを測ること
物理学の測定というのは、基本的には長さを測ることに帰着する。その理由は、物理というものは、色やにおいや音などのさまざまな現象を粒子の位置で説明しようとする試みだからだと思う。そして位置を測るとは、ある基準点からの長さを測ることなわけだから、物理とは、この世界を長さで説明しようとする試みなわけである。これは人の心に自然に浮かんでくる世界像ではないだろうか。デカルトもこのような世界像をいだいていたし、古代ギリシャ人のデモクリトスやエピクロスもいだいていた。長さを測るとは、基準となるものさしの端と端で位置の一致を確かめて測るわけである(図6.1)。その一致は、目か、さわった感触で確かめるわけである。ところで
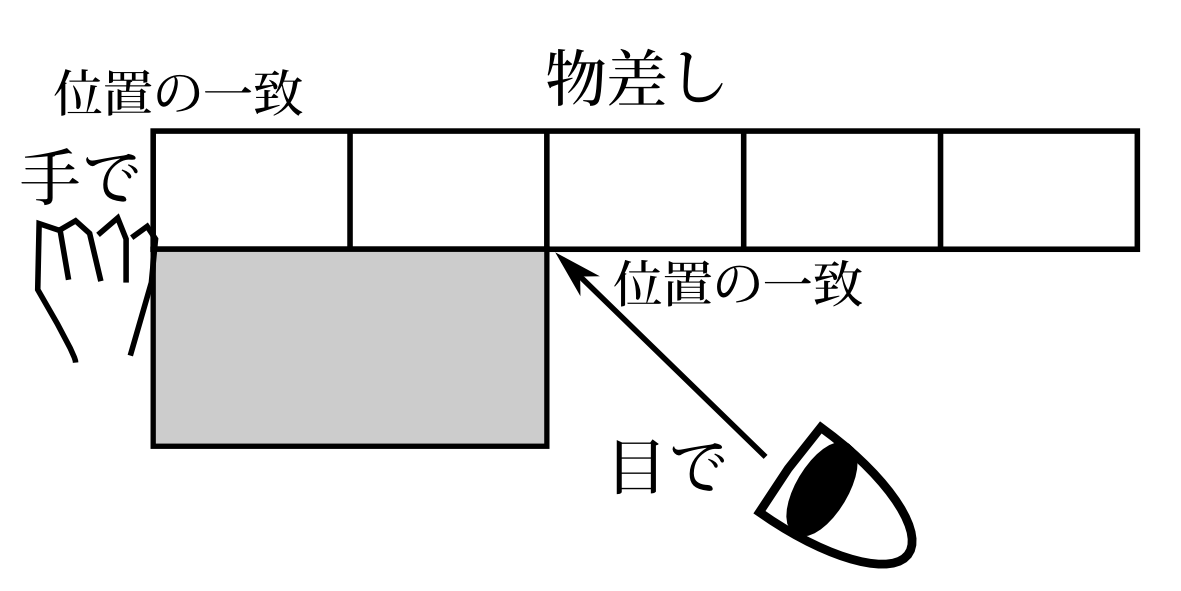
図6.1
我々には五感がある。自然法則というものは、感覚と感覚の関係だと言える。長さですべてを説明するとは、長さですべての感覚を説明するということである。しかしながら、一体なぜ、多くの感覚があるのに、長さで他の感覚を説明しようとするのか。すべての現象を色やにおいで説明してもいいではないか。我々はリトマス紙の色で酸性かアルカリ性かを判断しているし、りんごの色で甘さを判断する。雲の色で大雨を予測もするではないか。これに明確に答えるのは難しいが、
測定とはある基準のものに等しいと判断する行為(又はそれとの比較)である。となるとそのためには長さを使うのがいいのである。その理由としては
1.固体の長さというものが時間が経っても、ほとんど変化しなという安定性
が理由の一つであろう。つまり、二つの棒の長さが一致していれば、次の日もほぼ一致しているわけである。においは時間とともにすぐ変わるし、色もすぐあせる。ただ、これは程度の問題ではある。又、もうひとつ理由として、
2.判断が人に依らないという客観性
がある。ある人が長さが等しいと判断すれば、おそらく別の人も等しいと判断しよう。色の場合は、同じ色だという判断が長さほどは人によって一致しない。においなどなおさらである。ただこれも程度の問題である。又、これは理由と言えるかどうかわからないが、
3.長さは等しいものに分割でき、又、それを合わせることができる。
つまり長さは数なのである。量と言ったほうがいいかもしれない。色やにおいは等しいものに分割できないのである。自然現象というものは連続である。痛いといっても程度があり、速いと言っても程度がある。言葉というものは不連続である。一方数は連続である。だからこの連続な自然を表すには数がいいのである。数とは、等しいものの集まりにおいて、それを数えたものであり、指で1個2個と数えるように一対一の対応のことである。
測定とは基本的に何か基準のものに等しいと判断することだが、私が思うに完全に等しいものは、長さ(つまり空間での等質性)と電子のような素粒子だけのような気がする。同じ色、同じ音と言っても実際は微妙な差があることだろう。そういうわけで、 測定とは基本的には長さを測るということであり、その前提でこれからの議論を進める。 それでは長さ以外の、例えば音で全ての現象を説明できないのか、と言えば、できると思う。というのは長さと音が一対一に対応していれば、音は長さに変換できるからである。そして例えばにおいを長さで説明できると言うなら、その長さを音に変換できるわけで、音によってにおいも説明できるというわけである。ただ実用的でないことは明らかである。
6.2節 粒子検出装置
測定とは基本的には位置を測ることであり、長さを測ることであるということを前節で述べた。量子力学で1つの粒子の物理量を測ろうと思えば、その粒子、又はその粒子と反応させた粒子の位置を測るしかないと思う。それでこの節では原子や電子のような微粒子の位置の測り方を述べたい。
霧箱
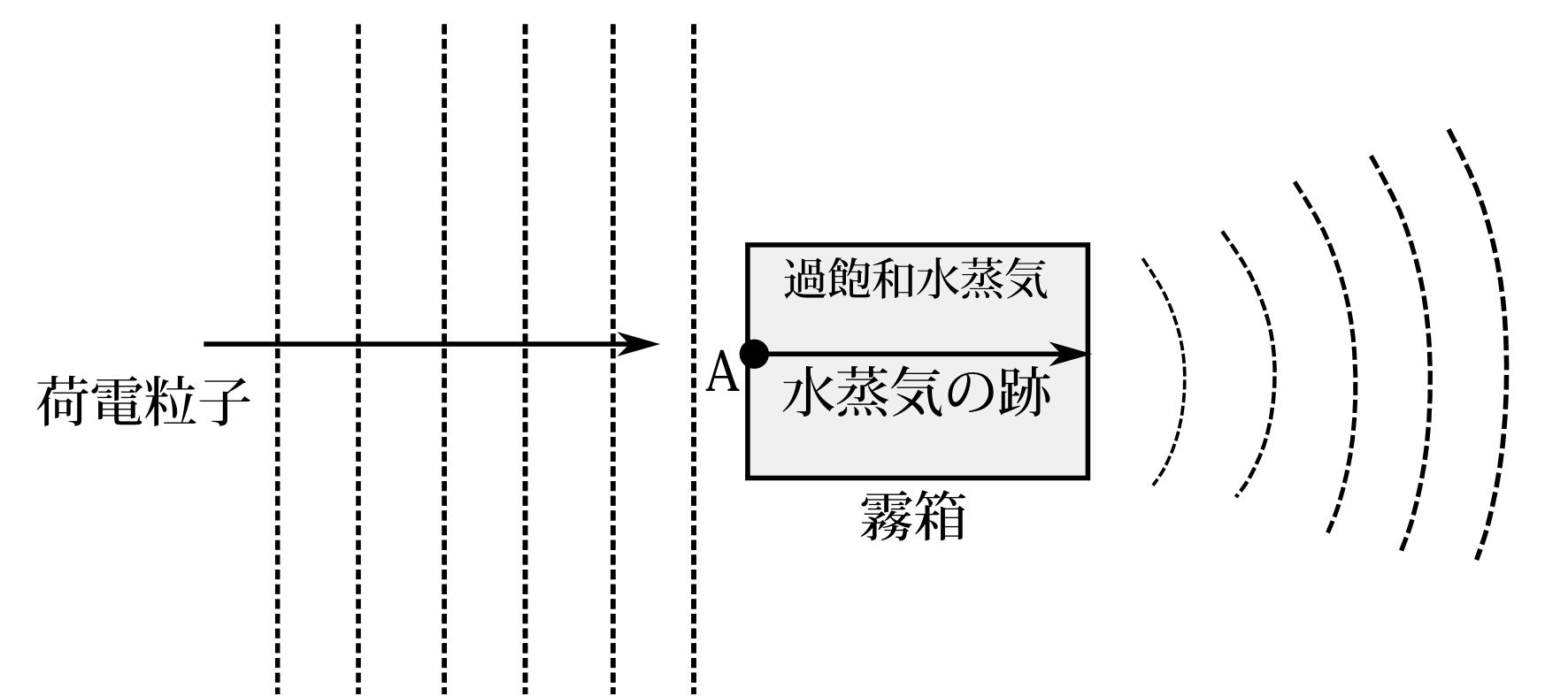
図6.2 霧箱。破線は波動関数の波の山を表す。粒子が霧箱に突入すると白い線が現れる。波動関数はその白い線上の点Aに収縮するはずである。
まず有名なものに霧箱がある(図6.2)。これは過飽和水蒸気中に荷電粒子を突入させると、それが刺激となって、粒子の通った跡に霧状の水滴ができるのである。写真で見たことがある人も多いだろう。粒子が通った跡がはっきりわかるのである。ただ肉眼で見えるくらいだから精度は悪い。混じり物のない純粋な水蒸気は液体になるべき温度まで冷えても液体にならない。雨が降るのも空中に核となるゴミがあるからである。荷電粒子が突入すると、細かい仕組みはわからないが、それが刺激となって水滴ができるのだと思う。ここで注目してほしいのは位置を測定しても軌跡は一定の向きを持って動いているということである。決して位置を測定したからと言って、運動量が全くわからない状態に移るのではないということである。粒子が霧箱に入ると白い線が見える。量子力学の法則によれば、その入った位置、図6.2では軌跡の左端の点Aに波動関数は収縮するはずである。そして運動量の確率分布はすべての運動量で等しいという状態になるはずである。しかしそうなっていない。位置の測定に幅があるからと考えるかもしれないが、それでも、運動量は左右両方向持っていなければならない。しかし 粒子は一定方向に向かって動いている。これは量子力学の法則に反することである。
ガイガーカウンター(放射線計数機)
ガイガーカウンターというのは名前しか知らず、これを書くために調べた。図6.3のようにガラス管の中にガスを入れる。\(\alpha\)線などの放射線が侵入するとガスは電子と+イオンに電離する。ガラス管の両端に高電圧をかけておけば電荷はそれぞれの極に移動し、電流が流れる。それを検知して放射線が侵入したことを知る。これだと位置の精度はガラス管の大きさ程度で、かなり粗い。
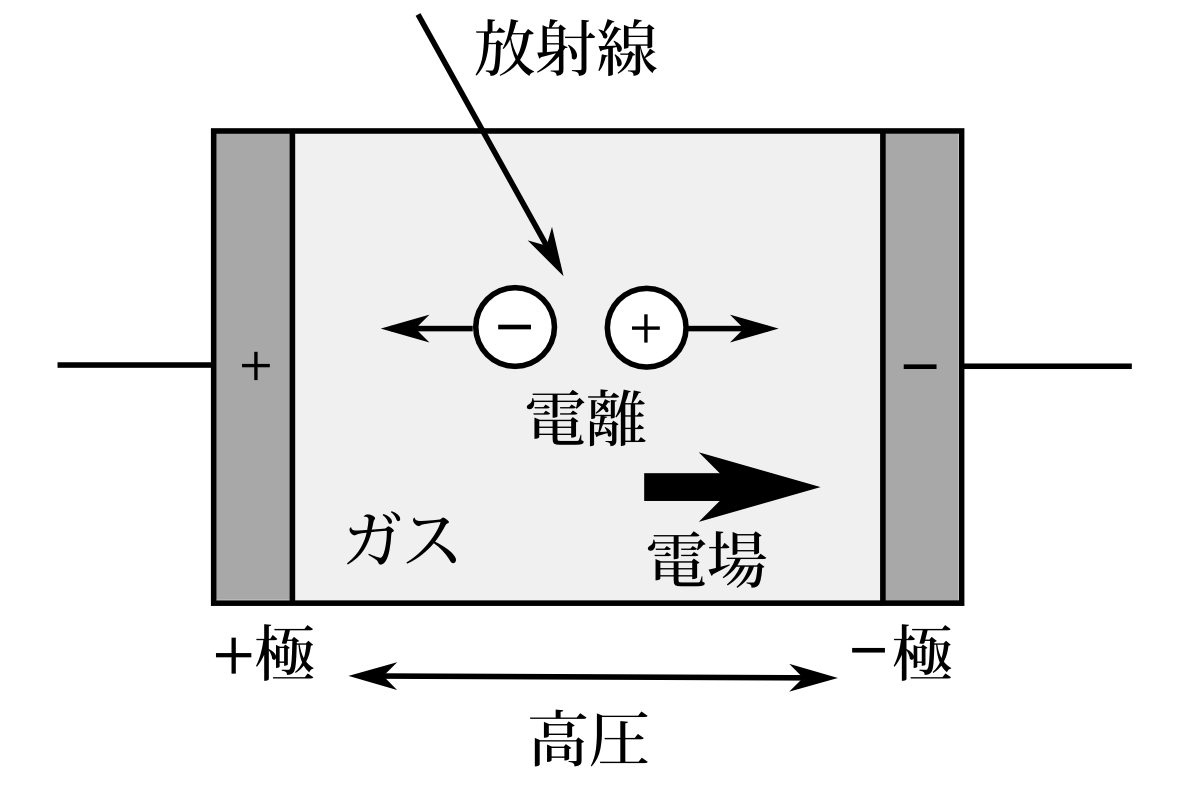
図6.3 ガイガーカウンター
光電子増倍管
光子を検出する装置として光電子増倍管がある(図6.4)。これは光の光電効果を使ったものである。光子が金属面に当たると電子が飛び出る。その電子に電場をかけて加速させてやり、次の金属面にあたるようにする。すると電子が何個か飛び出る。例えば5個としよう。その5個にまた電場をかけて、次の金属面に当たらせる。これを繰り返せば指数関数的に電子数が増え、やがて電流として検出される。これも位置の精度は悪い。

図6.4 光電子増倍管
こんなふうに粒子の検出はその粒子の効果を増幅することによって人間が知覚できるようにしているのである。電子一個、光子一個が目に入ってもそれに対して人間の肉体自体は物理的な反応はするだろうが、意識としては自覚できないのである。
6.3節 粒子検出の意味
粒子の検出があったと言えるためには、過程のある決定論としての物理法則が必要である。 例えば霧箱なら、我々には単に白い線が見えるだけである。その線上を荷電粒子が通ったと言えるためには、荷電粒子が過飽和水蒸気を刺激して水滴つくるということが法則として確立していなければならない。 光電子増倍管でも、我々が感知するのは単に電流が流れたということだけである。そこに光子が来たと主張できるためには 光子が金属にぶつかると電子が飛び出すという法則が確立していなければならない。光子が金属にぶつかって電子が飛び出すことは古典電磁気学では説明がつかないから、これは量子論かと言えば全くそういうことでなく、光子が金属にぶつかり電子が飛び出すという過程が決定論として確立しているならそれは、概念的には古典論に入る。このように過程が物理法則として確立していなければ電子が来たとか、光子が来たなどとは言えない。我々は直接電子を目で見えるわけではないのだから。そしてこの過程は必ず決定論(古典論)としての法則なのである。というのは 量子論では測定は瞬間である。あるとき運動量がどれだけだった、位置がどこそこにあった、というように瞬間である。 Aが起きたらBが起きるという過程がないのである。 古典論では過程がある。ある速度をもってある位置を通り刻々と変化する。ただ量子論でも波束には運動の過程がある。
量子論の測定では必ずこの決定論(古典論)の世界、現実の世界に入らなければならない。
その世界にいつ入るかだ。後の第7章で述べることだが、電場、磁場で軌道を曲げて運動量を測るとき、この曲げられる過程を古典論に入れてしまうか、粒子検出の過程から古典論に入れてしまうかだ。 決定論は正しくないのにそれを測定時の理論的根拠にしなければいけないというのは全くもっておかしな話である。
6.4節 位置の測定精度には限界があるか
位置検出器は人間の知覚の鈍さのため、かなりの大きさになる必要がある。 となると、位置は検出器の大きさ程度の精度でしか測ることができないのか、 位置を限りなく正確に測ることは出来ないのかと疑問が湧くと思う。 それについては粒子の位置というのが正確には何を意味するのかを明確にしなければ何も言えないと思う。電子がある位置から1nm以内に存在している、又は存在していたとは、いったい どういう物理的効果があるのか。そういうことをまず明確にしなければならないのだと思う。非常に素朴に考えれば、位置の精度には限度はないと思う。そのことを光学顕微鏡を用いて簡単に説明しよう。
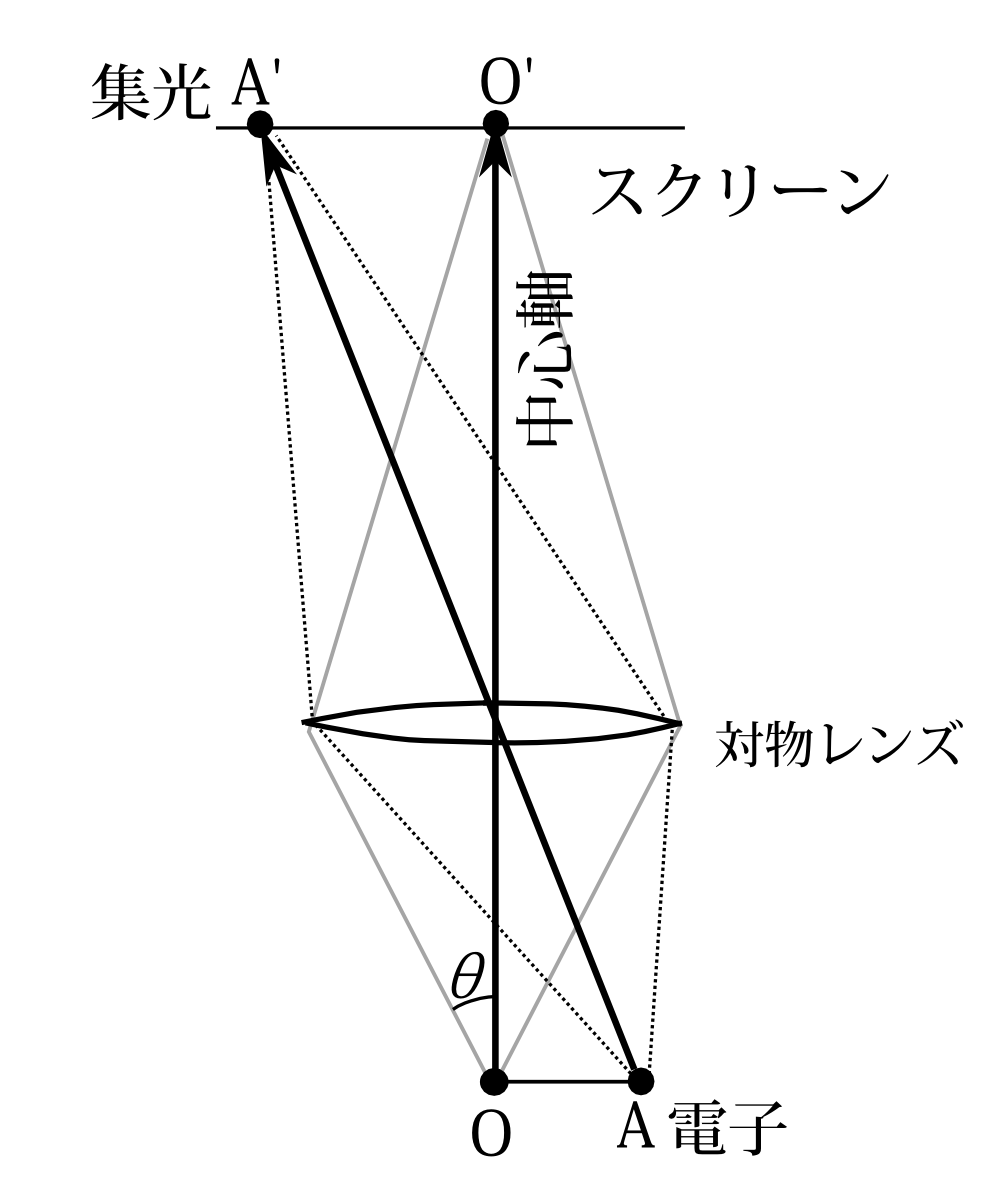
図6.5 光学顕微鏡で電子の位置を測る。
図6.5のように、電子に光をあてて、その散乱した光をスクリーン上に集光させる。光はスクリーン上の点A'に集光したとしよう。顕微鏡の中心軸上の点O'とA'との距離を測って、電子が中心軸上の点Oからどれだけ離れていたかを知ろうというわけである。スクリーンには光子の検出器があるわけだが、検出器の大きさの分だけ誤差がある。又、集光した光の像にも広がりがあるのでその分も誤差になる。まず検出器の誤差を取り除くには倍率を上げれば良い。つまり、対物レンスを薄くして、スクリーンと対物レンズの距離を広げO'A'の距離を広げれば良い。そうすれば、検出器の大きさの誤差は相対的に小さくなる。光の像の広がりを小さくするには対物レンズを広げればよい。顕微鏡での位置の精度は、\(\lambda\)を光の波長、\(\theta\)を軸と対物レンズの開きの角度として、\(\lambda/\sin\theta\)と考えられる(9.4節参照)。\(\theta\)を広げれば、精度はいくらでもよくなる。
しかしながら、これは光が波として振る舞うとしての理屈であって、実際は光は粒子として検出される。それゆえ位置の精度として、この\(\lambda/\sin\theta\)を使うことには問題がある。それに光の回析のために、位置の精度について、この範囲に100%存在すると断定することはできない。ここらへんは9.6節でも述べているので参照して欲しい。そういうわけで、位置を限りなく正確に測ることができるかという問題は、今のところ、私にはわからないし、最初に述べたように、位置がこの範囲に存在するということがいったい何を意味するのかを――もちろん直接検出器で検出されれば別だが――明確にしなければ答えられない。そしてその「意味を明確にする」ことが難しいのだと思う。
6.5節 量子論での運動量、エネルギーなどは何を意味するか
量子論と古典論では物理量の概念が異なる。例えば、エネルギーは\(\frac{p^2}{2m}+V\)(運動エネルギーと位置エネルギーの和)であるが、量子論によれば同時刻の位置と運動量を両方正確に決めることはできないということになっている。ということは運動エネルギーと位置エネルギーを同時に正確に決めることができないということであり、エネルギーの値を正確に決めることはできないはずである。ところが量子論によれば正確に決まるのである。だから量子論と古典論でのエネルギーの概念は全く同じとは言えない。しかし全く別物というわけでもない。
量子論での物理量も粒子がたくさん集まれば、その和は古典量と一致していなければならない
はずだ。量子論的にエネルギー\(\varepsilon\)の粒子が\(N\)個集まれば、古典論ではそのエネルギーは\(N\cdot \varepsilon\)に近い値を示すだろう。量子論的に運動量\(p\)の粒子が\(N\)個壁に当たれば、壁は(粒子は吸収されるとして)運動量をおよそ\(N\cdot p\)受け取るはずである。