第10章 カノニカル分布での量子状態
統計力学によれば、ある温度\(T\)にある系の量子状態はエネルギー測定状態にあり、そしてエネルギー\(\varepsilon\)の測定状態にいる確率\(P_\varepsilon\)(これは日常用語の意味での確率で、量子力学的確率ではない)は \begin{equation} P_\varepsilon=\frac{e^{-\beta \varepsilon}}{\sum_\varepsilon e^{-\beta\varepsilon}} \label{kano} \end{equation} である。ここで\(\beta=1/kT\)で、\(k\)はボルツマン定数。いわゆるカノニカル分布というものである(この章での話はもちろんミクロカノニカル分布でも通用な話であるが、カノニカル分布での話とする。)。しかしながら、系がエネルギー測定状態にいるというのはどう考えても不自然である。エネルギーを測ったわけではないのである。いったい何を持ってある温度の平衡状態にある系がエネルギー測定状態にあるといえるのだろうか。ではどういう状態にいるかというと、 いわゆるエネルギー測定状態の重ね合わせで、 エネルギー\(\varepsilon\)である確率振幅\(\varphi_\varepsilon\)が、(\ref{kano})の\(P_\varepsilon\)を用いて \begin{equation} \varphi_\varepsilon= \sqrt{P_\varepsilon}e^{i\delta_\varepsilon} \label{ccc1} \end{equation} となる状態にあると考えるのが自然である。ここで\(e^{i\delta_\varepsilon}\)はエネルギー\(\varepsilon\)ごとに異なる不定の位相因子で\(\delta_\varepsilon\)は実数である。この状態でエネルギーを測定すればそれが\(\varepsilon\)である確率は\(P_\varepsilon\)になってくれる。あとの理論展開は通常の統計力学と全く同様に行くと思うのだがどうだろうか。 私は長い間統計力学を勉強していないので詳しく書けないのが残念なのだが。
思考実験
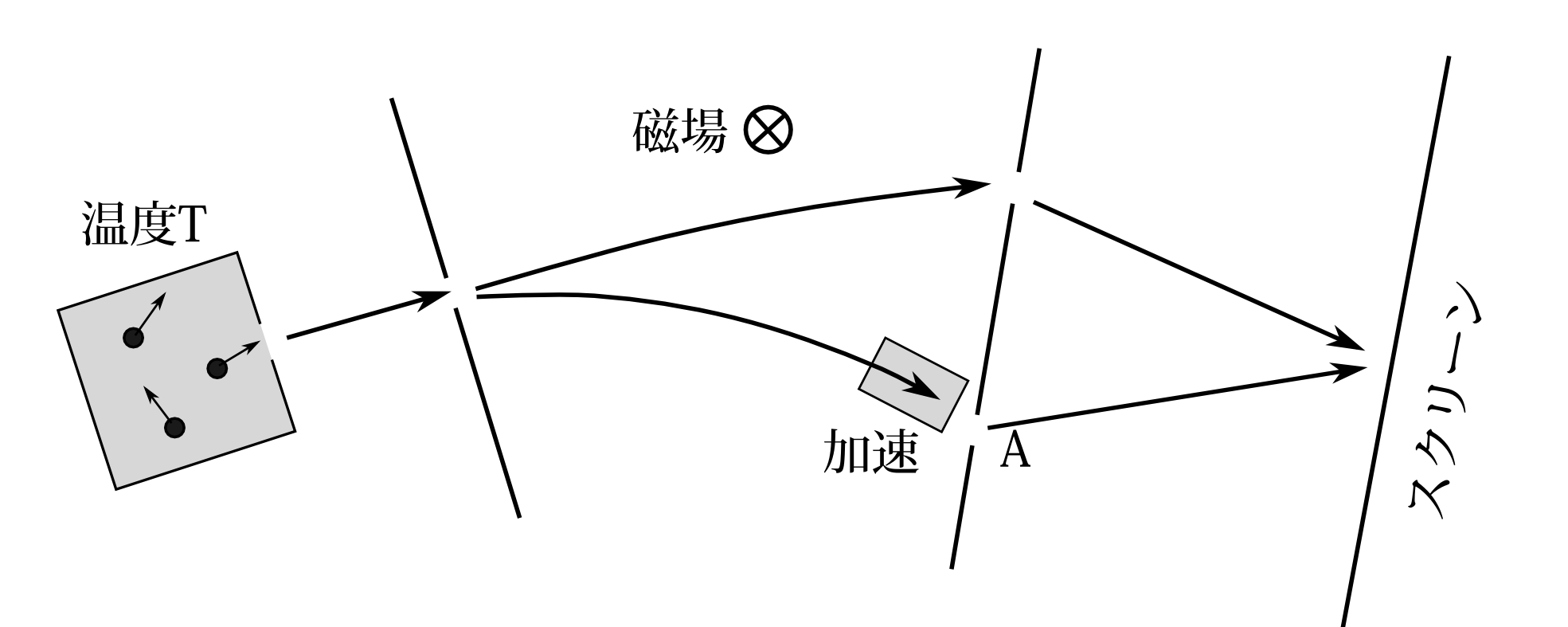
図10.1
この(\ref{ccc1})が正しいのかどうかを試す思考実験がある。図10.1 のようにイオン気体の入った箱に穴をあけて分子が飛び出るようにする。シャッターなどを用いて同時に複数の粒子が飛び出ないようにする。その粒子を速度によって分離できるようにする。例えば磁場をかけるなどする。遅い方の軌道は電場などで加速させて、もう一方の軌道の速さと等しくなるようにさせて、スリットAを通るようにさせる。 このときスクリーンに干渉縞ができるかどうかというのが問題である。もし通常の量子統計力学の解釈なら、粒子はどれかのエネルギー測定状態にあり、どの測定状態にいるかは我々は知らないだけであり、波動関数は磁場で分離しない。そして干渉縞は現れない。しかし量子状態が(\ref{ccc1})で表されるなら、干渉縞が現れるはずである。同じような実験がスピンでもできそうである。