第9章 不確定性原理
この章では不確定性原理について述べる。不確定性原理というのは量子力学の基本法則から導ける定理(注 通常「原理」というのは何か自然界で成り立つ非常に普遍的法則を述べたものを呼ぶときに使うようである。例えば、相対性原理、熱力学でのクラジウスの原理、エネルギー不変の原理などである。具体的な実験数値や数式で表されるようなもの、例えばクーロンの法則のようなものには「原理」という言葉は使わないようである。 )である。それは運動量から位置への確率振幅の変換行列が\(e^{ip\cdot x/\hbar}\)であることから出てくる。 ハイゼンベルグの顕微鏡の思考実験を中心に考察し、その問題点を指摘する。私は不確定性原理というものは、あまり重要ではないと思っている。一つには不確定性原理は量子力学の体系の中では一つの定理でしかないし、もう一つには、位置と運動量の定義が――――特に運動量が――――明確でないのに、その精度を論じてもあまり意味がないと感じるのである。又、不確定性原理の証明自体にも問題があるからである。
9.1節 不確定性定理
まず、量子力学の法則から不確定性定理を導こう。不確定性定理というのは
【不確定性定理】 どんな状態でも、 位置の\(x_i\)成分の確率分布がおよそ0でないような\(x_i\)の範囲\(\Delta x_i\)と運動量\(p_i\)成分の確率分布がおよそ0でないような\(p_i\)の範囲\(\Delta p_i\)は \[ \Delta x_i\Delta p_i>h \] を満たす。ここで\(h\)はプランク定数。
というものである。 この証明に使う量子力学の法則は、運動量から位置への確率振幅の変換行列が\(e^{ip\cdot x/\hbar}\)である ということである。そして波数\(k=2\pi/\lambda\)の範囲\(\Delta k\)と波束の範囲\(\Delta x\)の間に\(\Delta x\Delta k>2\pi\)の関係があるという、よく知られている数学的な事実を使う。
証明
それでは、この定理を証明しよう。一般に、関数\(f(x)\)をフーリエ級数に展開した \[ f(x)=\sum_k e^{ikx}g(k) \] では、\(f(x)\)がおおよそ0でない範囲\(\Delta x\)と、\(g(k)\)がおおよそ0でない範囲
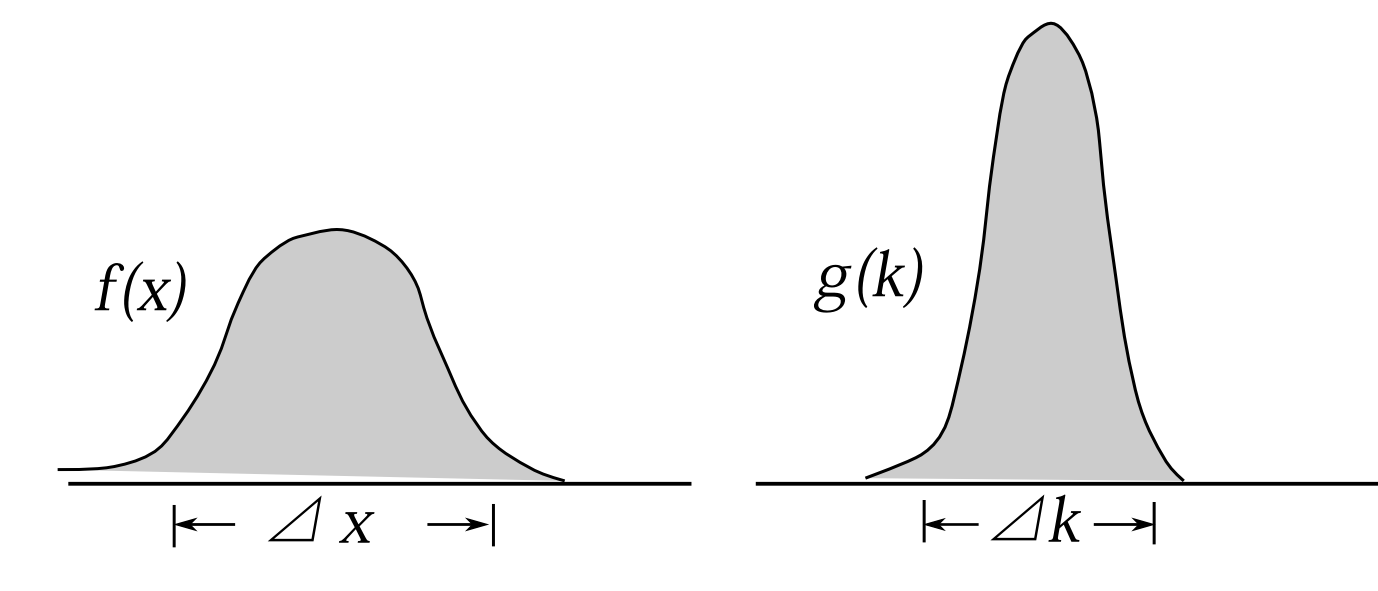
図9.1
\(\Delta k\)(図9.1参照) の間で \begin{equation} \Delta x\Delta k>2\pi \label{k2-2} \end{equation} が成り立つ。これは物理とは一切関係ない数学的事実である。多くの物理の教科書、主に波についての箇所で記載されているのでこれが成り立つ理由は省く。
さて、この不確定性定理は何粒子であろうと何次元であろうと成り立つのだが、記号を簡素にするために、\(x,y\)の2次元の場合で証明する。位置\(x,y\)の確率振幅\(\psi(x,y)\)と運動量\(p_x\)、位置\(y\)の確率振幅\(\varphi(p_x,y)\)との間の変換は \begin{equation} \psi(x,y)=a\sum_{p_x}e^{ip_x\cdot x/\hbar}\varphi(p_x,y) \label{1219a} \end{equation} である。ここで\(a\)は規格化定数。 \(y\)を固定すれば、これは\(x\)についてフーリエ展開した式になっている。\(x\)を動かして\(\psi(x,y)\)がおよそ0でない\(x\)の範囲は確率分布\(P(x,y)\)がおよそ0でない範囲\(\Delta x\)と一致する。また\(p_x\)を動かして\(\varphi(p_x,y)\)がおよそ0でない\(p_x\)の範囲は確率分布\(P(p_x,y)\)がおよそ0でない範囲\(\Delta p_x\)と一致する。だから、(\ref{k2-2})を使うと \[ \Delta x\cdot \Delta\left(\frac{p_x}{\hbar}\right)>2\pi \] が成り立つことになる。\(\hbar=h/2\pi\)なので \[ \Delta x\Delta p_x>h \] が成り立つ。これが不確定性定理が成り立つ理由である。
補足
この定理について少し補足しよう。少し細かい話なので飛ばしてもらって差し支えない。 今の場合\(y\)を固定したが、これは何でもよくこれが\(p_y\)であっても――――といっても今は2次元としているので\(p_y\)しかないのだが――――(\ref{1219a})が \[ \psi(x,p_y)=a\sum_{p_x}e^{ip_x\cdot x/\hbar}\varphi(p_x,p_y) \] となるだけで、残りの議論はそのまま成り立つ。だから\(x\)と\(p_x\)の確率分布として \(P(x,p_y)\)と\(P(p_x,p_y)\) を採用しても不確定性定理が成り立つ。尚、\(P(x,y)\)と\(P(p_x,p_y)\)というような固定するものが\(y\)と\(p_y\)というように異なるものは物理的に意味をなさない。
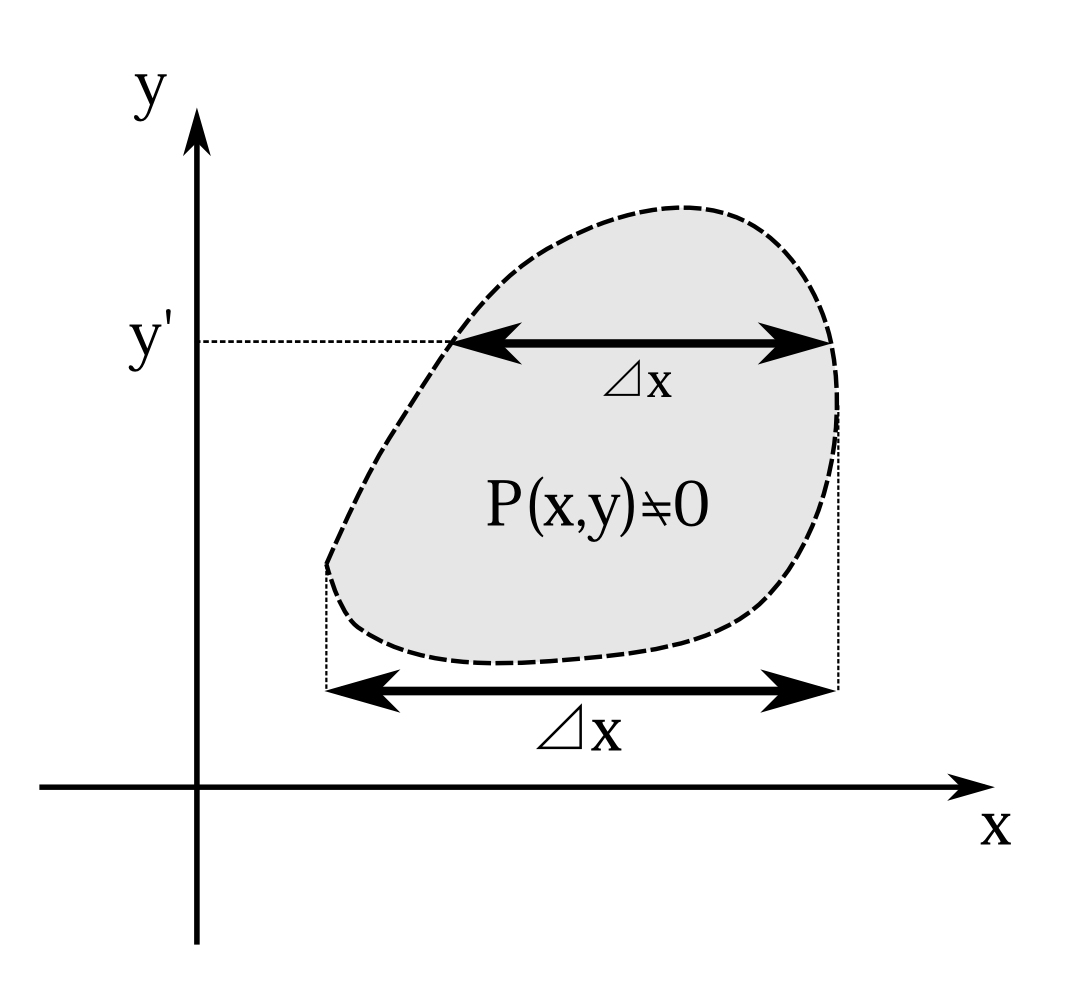
図9.2 破線の中が確率分布\(P(x,y)\)がおよそ0でない範囲。\(y\)を固定したときの分布がおよそ0でないような\(x\)の範囲より、すべての\(y\)の範囲での、分布がおよそ0でないような\(x\)の範囲の方が広い。
又、証明では着目している測定変数以外は固定したが、和を取るという確率分布も考えられる。例えば \[ \sum_y P(x,y)\qquad \sum_y P(p_x,y) \] というのも\(x\)と\(p_x\)の確率分布になる。この場合でも不確定性定理は成り立つ。それは図9.2を見てもらえればわかるように、ある\(y\)を固定して\(P(x,y)\)がおよそ0でない\(x\)の範囲より、すべての\(y\)での\(P(x,y)\)がおよそ0でない\(x\)の範囲の方が――――等しいか――――広くなる。となると\(\sum_yP(x,y)\)がおよそ0でない\(x\)の範囲は、ある\(y\)を固定して\(P(x,y)\)が0でない\(x\)の範囲より広くなる。実際のところは、およそ0でない範囲というあいまいな定義なのでこのようには断定できないが、この不確定性定理自体、およそのことを言っているのでこれでいいと思う。
さらに細かい話をするが、今は\(y\)で和を取ったが、これは\(p_y\)で和をとってもよい。というのは和はどの変数でとっても同じ値になるからである。つまり \[ \sum_y P(x,y)=\sum_{p_y} P(x,p_y) \] が成り立つからである。この証明は――――そんなに難しくないのですぐできるのだが――――省くが、確率振幅の変換行列がユニタリーだからである。
今の不確定性定理の説明では確率分布がおよそ0でないという、やや曖昧な表現を使った。そうでなくより数学的正確さを持って言うと、\(x_i\)と\(p_i\)の分散\(\left\langle (\Delta x_i)^2\right\rangle ,\left\langle (\Delta p_i)^2\right\rangle \)については (注 これは \[ \left\langle (\Delta x_i)^2\right\rangle =\sum_\text{all} (x_i-\left\langle x_i\right\rangle )^2P(x_i,x_他) \] という意味。ここで\(x_他\)は\(x_i\)以外の変数であり、又、和はすべての位置変数で取っている。 ) \[ \left\langle (\Delta x_i)^2\right\rangle \;\left\langle (\Delta p_i)^2\right\rangle \ge\frac{\hbar^2}{4} \] が成り立つ。その証明は砂川重信の「量子力学」53ページ。JJ桜井の「現代の量子力学(第1版)」の47ページ に出ている。ただ何かわかったような気がしない証明ではある。
9.2節 不確定性原理の意味
次にハイゼンベルクの言う不確定性原理について述べたい。このことについての知識は主にハイゼンベルクの書いた「量子論の物理的基礎」によっている。書かれたのは1930年で量子力学が出来て数年の頃である。
ハイゼンベルクの言う不確定性原理というのは不確定性定理同様 \[ \Delta x\Delta p>h \] という式である。式は同じなのだが、ハイゼンベルクの上記著書によると、この\(\Delta x,\Delta p\)は確率分布のおよそ0でない範囲ということでなく、\(\Delta x\)は粒子がその範囲にいるという意味で\(\Delta p\)は粒子の運動量の値がその範囲にあるという意味で使っているようである。そこが不確定性定理と少し違うところであるが、よくよく考えれば言っていることは同じである。そのことはすぐ後で述べる。
一つ大事な注意をしたい。それは、この\(\Delta x,\Delta p\)は 現在の測定での範囲ということであり、決して過去の測定での範囲ではないということである。現在の測定とは、この\(\Delta x,\Delta p\)が 予測できる値だということである。この「予測できる」と言われても意味がピンとこないと思うので1つ例を示そ
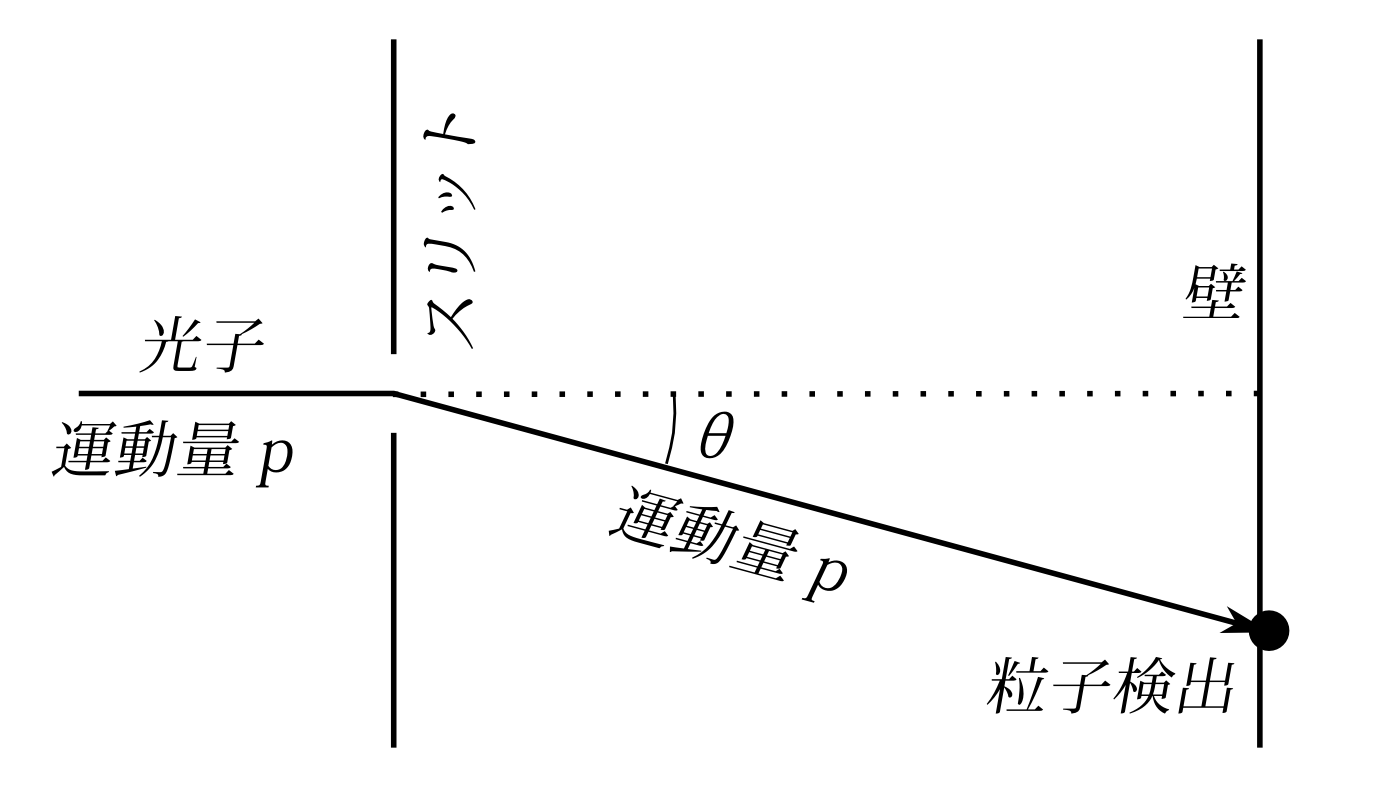
図9.3
う。図9.3のように運動量のわかっている(波長のわかっている)光子(電子でも良い)がスリットを通って壁に当たり、位置が検出されたとしよう。光子はスリット通過しても運動量の大きさ自体は変化しないとしよう。 このことは自明でも全く無いが、今は「予測できる値」の説明のために使っているので気にしないでもらいたい。 。それで光子がスリットを通過した瞬間の縦方向の位置と運動量を求め、その精度を知りたいとする。縦方向のスリット通過時の運動量は、図9.3にあるように、運動量の大きさを\(p\)、角度の変化量を\(\theta\)とすると、\(p\sin \theta\)である。しかし、スリットの大きさと、検出器の大きさの分だけ誤差がある。 一方スリット通過時の位置の精度はスリットの幅だが、これはスリットを小さくすればいくらでも精度を上げることができる。また運動量の精度も粒子検出器での誤差だけになる。\(\Delta x\to 0\)で\(\Delta p\)は有限、よって\(\Delta x\Delta p\to 0\)となる。又、さらに言えば、スリットと壁の距離を広げれば\(\Delta p\)もいくらでも小さくできる。つまり、スリットを小さくし、壁をスリットから遠ざければ\(\Delta x\to 0,\Delta p\to 0\)となる。 だから不確定性原理は成り立たないと言うことになってしまう。 しかしながら、この\(\Delta x,\Delta p\)は過去の位置と運動量の精度というわけである。粒子を検出してしまった後ではもう粒子はスリットにはいないのである。予測できる値というのは、今から測定すればこの範囲にいると予測できるということである。だからハイゼンベルクの不確定性原理も、最初に述べた不確定性定理もほぼ同じ意味なのである。今現在この範囲にいることがわかっているということは、まさに実際に測れば、確率分布がその範囲に収まるといういうことなのだから。
ただ細かいことを言えば今の説明にも問題はあるのである。これは第7章でも書いたが、粒子は量子力学の時間発展方程式に従って進行するのであり、古典軌道を通るわけではない。だから運動量を安易に\(p\sin\theta\)であるとも言えないし誤差についても上に書いたようには言えないと思う。ただ今は「予測できる測定」の説明の例として使っただけなので、先に進もう。
9.3節 ハイゼンベルクの顕微鏡
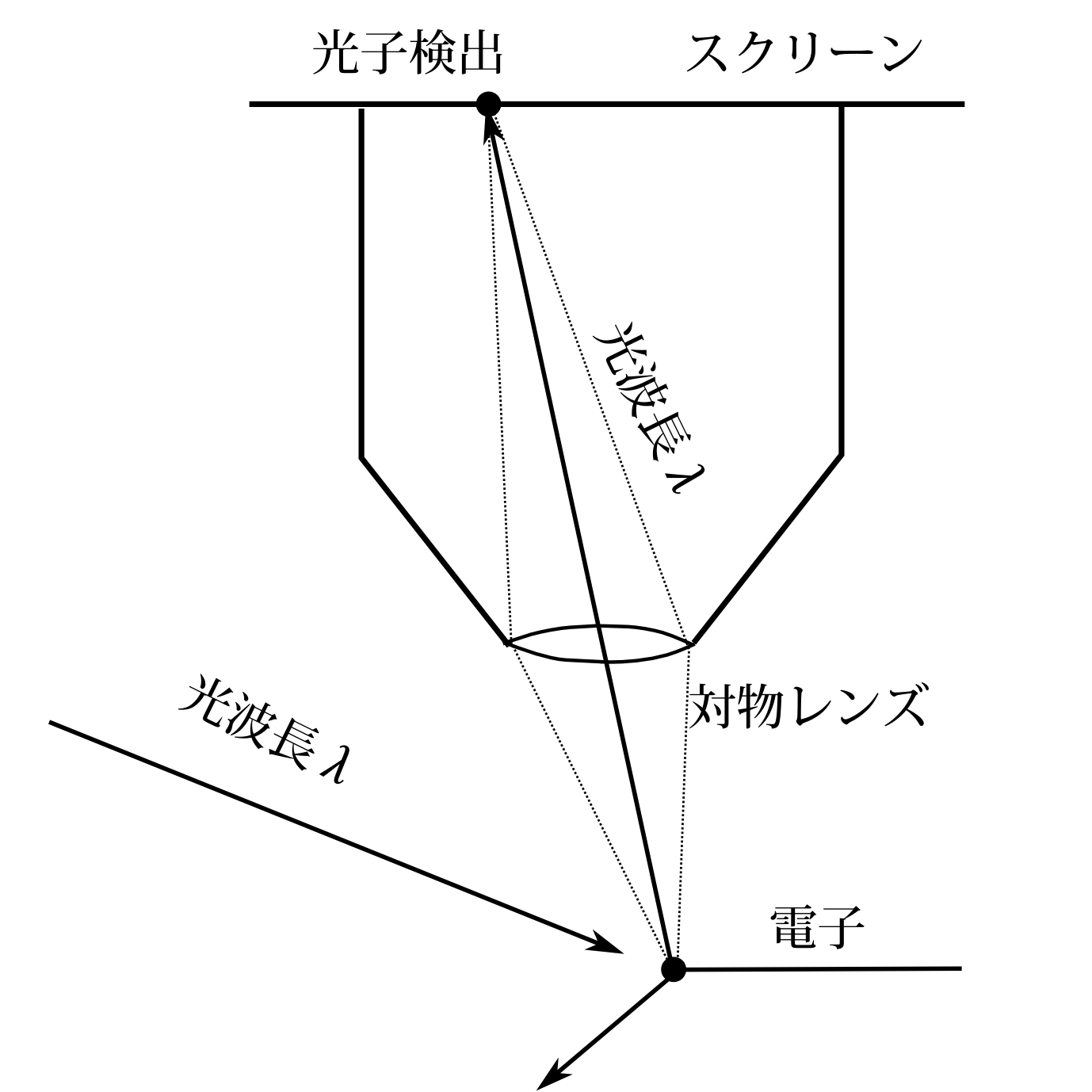
図9.4
有名なハイゼンベルクの顕微鏡の思考実験について考えよう(図9.4)。この思考実験はハイゼンベルグの著書「量子論の物理的基礎」に出ているし、多くの量子力学の教科書に出ているものである。 測定するものは電子とする。 これに波長のわかっている光をあてて電子の位置をスクリーンに映そうというわけである。電子に当たった光は散乱され、その一部が対物レンズに集められ、その後何枚かのレンズを通るかして、スクリーンに集光する。実際の顕微鏡なら、接眼レンズがあり、接眼レンズ以外にも収差をなくすレンズもあろう。さらには目のレンズがあって、目の網膜に集光して像を作るのだろうが、今は話を簡単にするために、レンズは対物レンズのみとする。さて、そして光子はスクリーンで検出され、その位置は(そんなことは絶対にないのだが)誤差なく、正確にわかったとする。今はどんなに理想的な実験をしても位置と運動量の精度の積に限度があるということを証明したいので、どんどん都合よく理想化していいのである。そのような簡略化された顕微鏡の模式図が図9.4である。そこで問題となるのは、「この光子のスクリーンでの位置がわかったその瞬間、電子の位置と運動量はどの程度の精度でわかるのだろうか」ということである。
位置の精度
まず位置の精度\(\Delta x\)の限界だが、これはいわゆる顕微鏡の分解能になる。分解能とは、2点間を識別できる限界の距離のことであり \begin{equation} \frac{\lambda}{\sin\theta} \label{bunka} \end{equation} となる。こうなる理由は後で書く。ここで\(\theta\)は図9.5の通り、レンズの軸と
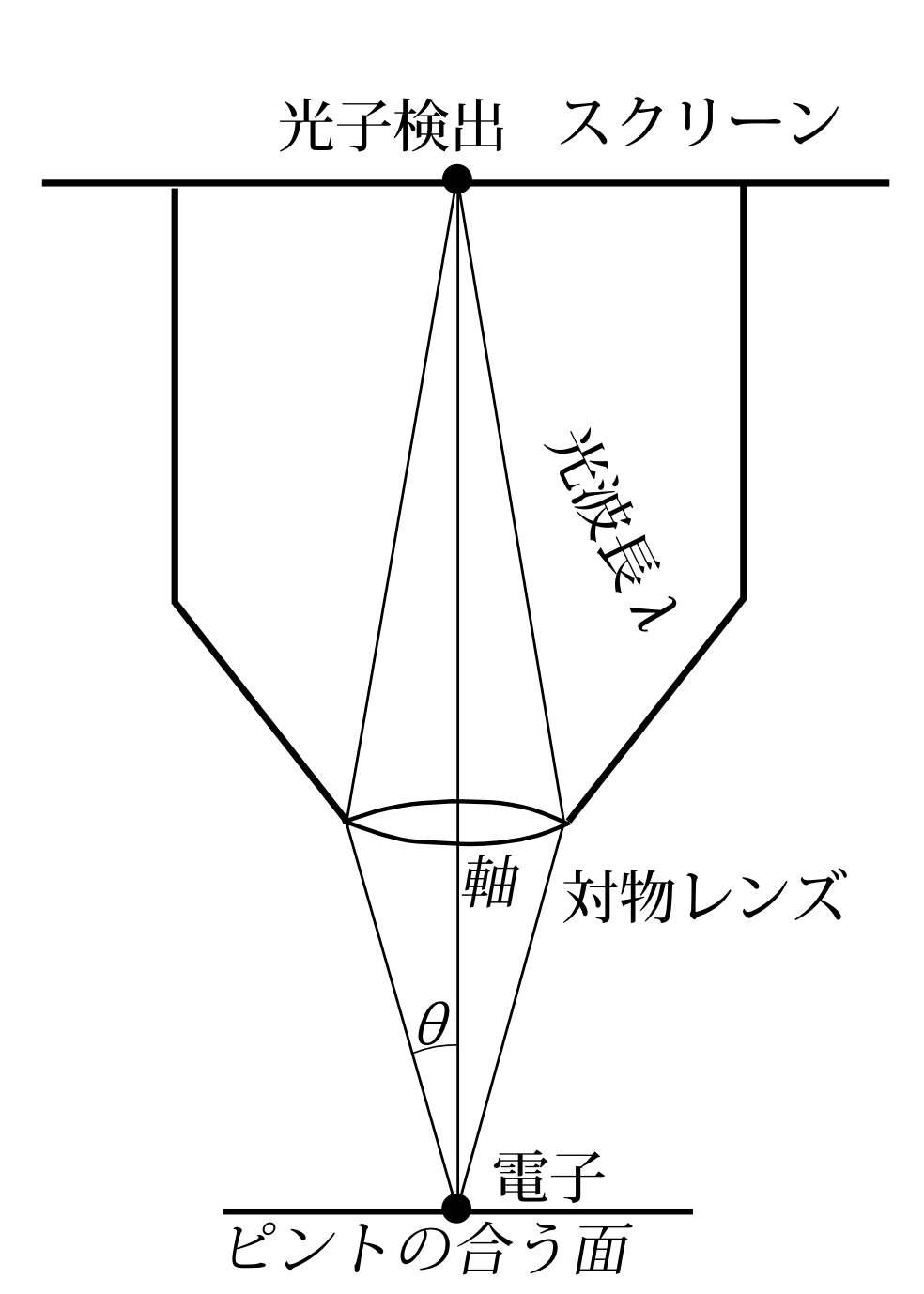
図9.5
電子のあるピントの合う面(この面はレンズの軸と直角で、この面上から発せられた光はスクリーンで集光するという面)との交点から対物レンズの端を結ぶ線とレンズの軸との角のことである。\(\lambda\)は電子から散乱された光の波長。これは散乱前の波長と同じとする。 本当は光は電子との衝突によって波長が変化するが(コンプトン効果)、それは話の大勢には影響ない。結局位置の精度\(\Delta x\)の限界がこの分解能ということなので \begin{equation} \Delta x\ge \frac{\lambda}{\sin\theta} \label{m1} \end{equation} となる。
運動量の精度
次に運動量の精度について考える。 光子は電子に衝突して、対物レンズを通ってスクリーンで検出されたのだが、対物レンズのどこを通ったかはわからない。衝突後の光子の運動量を\(p\)とすると、衝突後の横方向の運動量は\(-p\sin\theta\)から\(+p\sin\theta\)の範囲である(図9.6)。 今、例え衝突前の光子と電
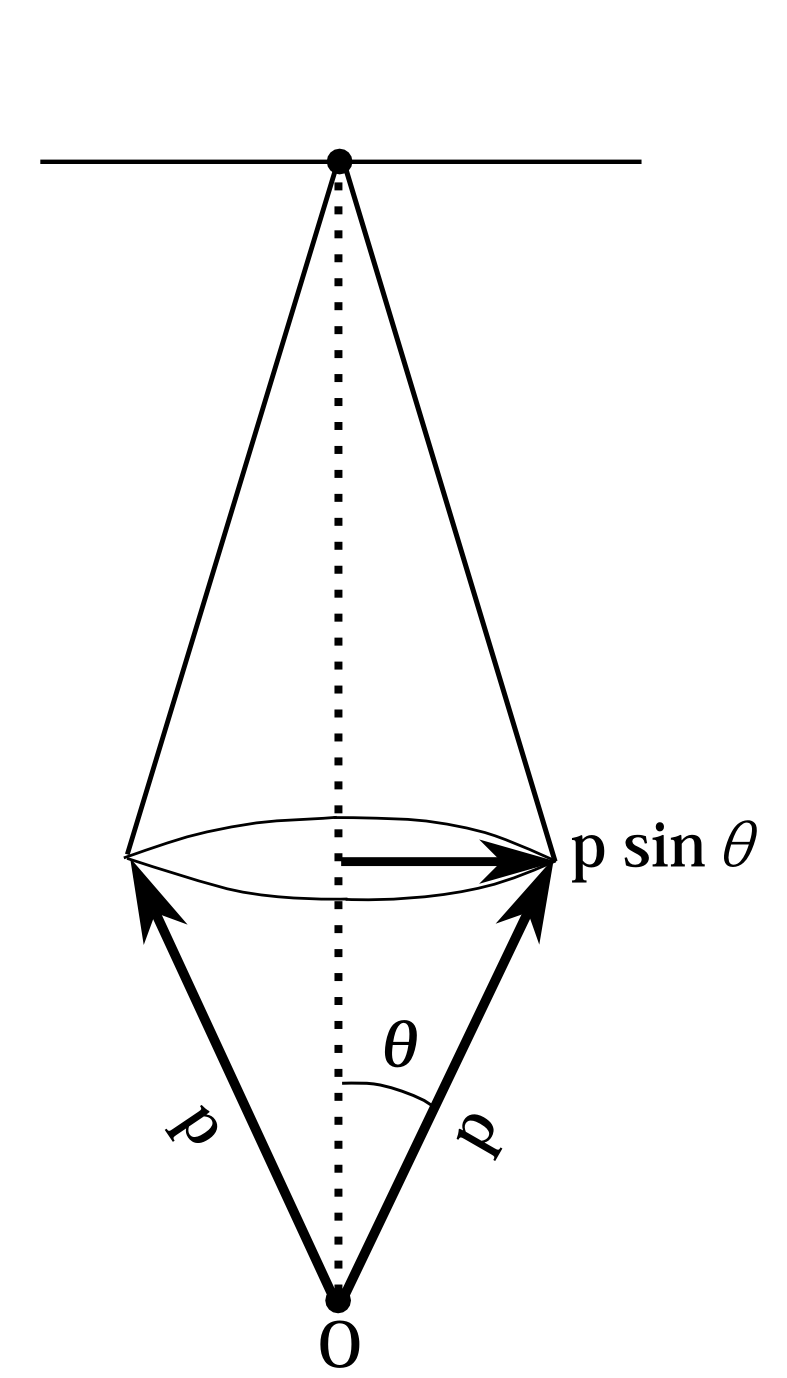
図9.6
子の運動量が完全に正確にわかっていたとしても、衝突後の光子の運動量はこれだけわからないわけだから、運動量の保存から――――量子力学の世界で運動量が保存するという保証はどこにもないのだが――――衝突後の電子の運動量も少なくとも、これだけはわからなくなるというわけである (注 これはいわゆるコンプトン散乱というもので光子の散乱方向によって波長は変化する。ただ、どの方向でも運動量の大きさを同じとしても大勢には影響ないだろう。)。 だから運動量のわかっている範囲\(\Delta p_x\)は \begin{equation} \Delta p_x\ge 2p\sin\theta \label{m1-1} \end{equation} である。
さて、スクリーンで光子検出後、電子の位置のわかっている範囲は(\ref{m1})式と運動量のわかっている範囲(\ref{m1-1})式より \[ \Delta x\Delta p_x\ge 2p\lambda \] となる。\(p=h/\lambda\)なので \begin{equation} \Delta x\Delta p_x\ge 2h>h \label{p1} \end{equation} となるわけである(注 実際は光子検出の時は、電子と光子が衝突したより後である。通常、シュレディンガー方程式に従う波束は時間とともに広がると考えられる。だから、電子の位置のわからなさの範囲は、\(\frac{\lambda}{\sin\theta}\)より広がる。ただ、今証明したいことは\(\Delta x\Delta p_x>h\)という不等式なのだから、\(\Delta x\)が、本文で想定してたものよりさらに大きくなるというのだから、この不等式が成り立つことには変わりないわけである。)。 これがハイゼンベルクが言っていることだろうと、私が解釈したものである。
9.4節 分解能
なぜ分解能が式(\ref{bunka})で記した\(\frac{\lambda}{\sin\theta}\)で与えられるかを書こう。 光は波として進行するので、一点から出た光は、スクリーン上である程度広がりを持つ。図9.7にあるように、一点から出た光のスクリーン上での強度分布は、一つ

図9.7 図の上部の線は2点からでた光のそれぞれの強度分布を表す。実線と破線に分けて、わかるようにしてある。強度の最初の山の範囲をその点から出た像と呼ぶことにする。この像がくっついてしまうと位置が区別できなくなる。
の高い山があり、一旦0になりそして小さな山と谷を繰り返す。それで一番大きな山の範囲をその点による像と呼ぼう。 測定される2点が近いとこの像はくっついてしまって識別できない。この像が離れるために必要な2つの対象物体の最小距離のことを分解能という(図9.7、図9.8)。その距離を求めるには光路差を考えればよい。

図9.8 スクリーン上の2点からでた光の像。この2つの像がくっつかないための、測定物間の最小距離が分解能
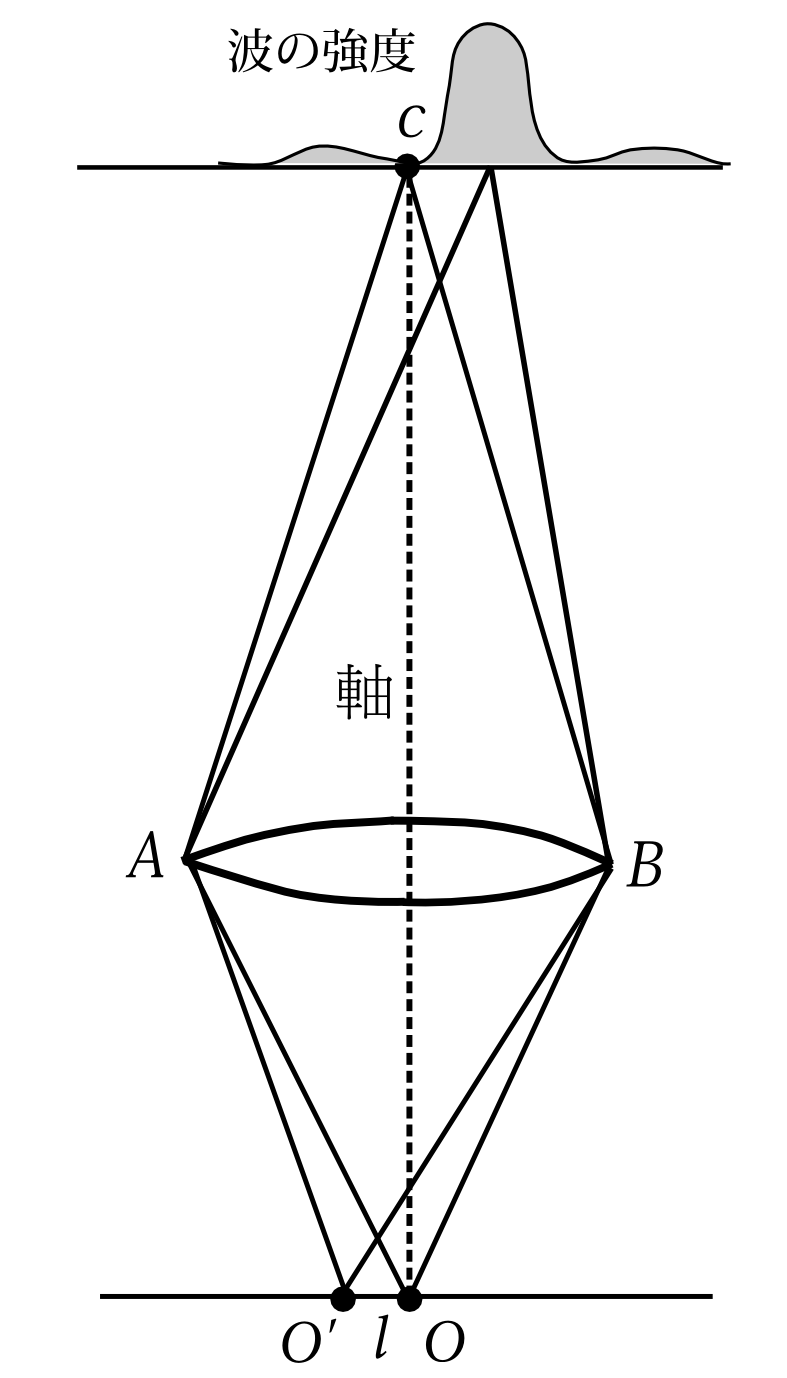
図9.9
図9.9のようにピントの合う面とレンズの軸との交点を点Oとする。又、レンズの端点をA、Bとする(直線ABがレンズの直径となるような端点である)。 点Oから出た光はレンズに向かって広がり、スクリーンの中心Cに同位相で集光する。 点Oから左へ徐々に移動させると像は右へずれていき、いずれ像の端が点Cに来る。そうなる点をO'とし、OO'の距離を\(l\)とする。図9.7を見ればわかることだが、\(2l\)が分解能となる。それでこの距離\(l\)を求めよう。 OAとO'Aの距離を比べると、\(l\)を微小とした近似では、図9.10のように
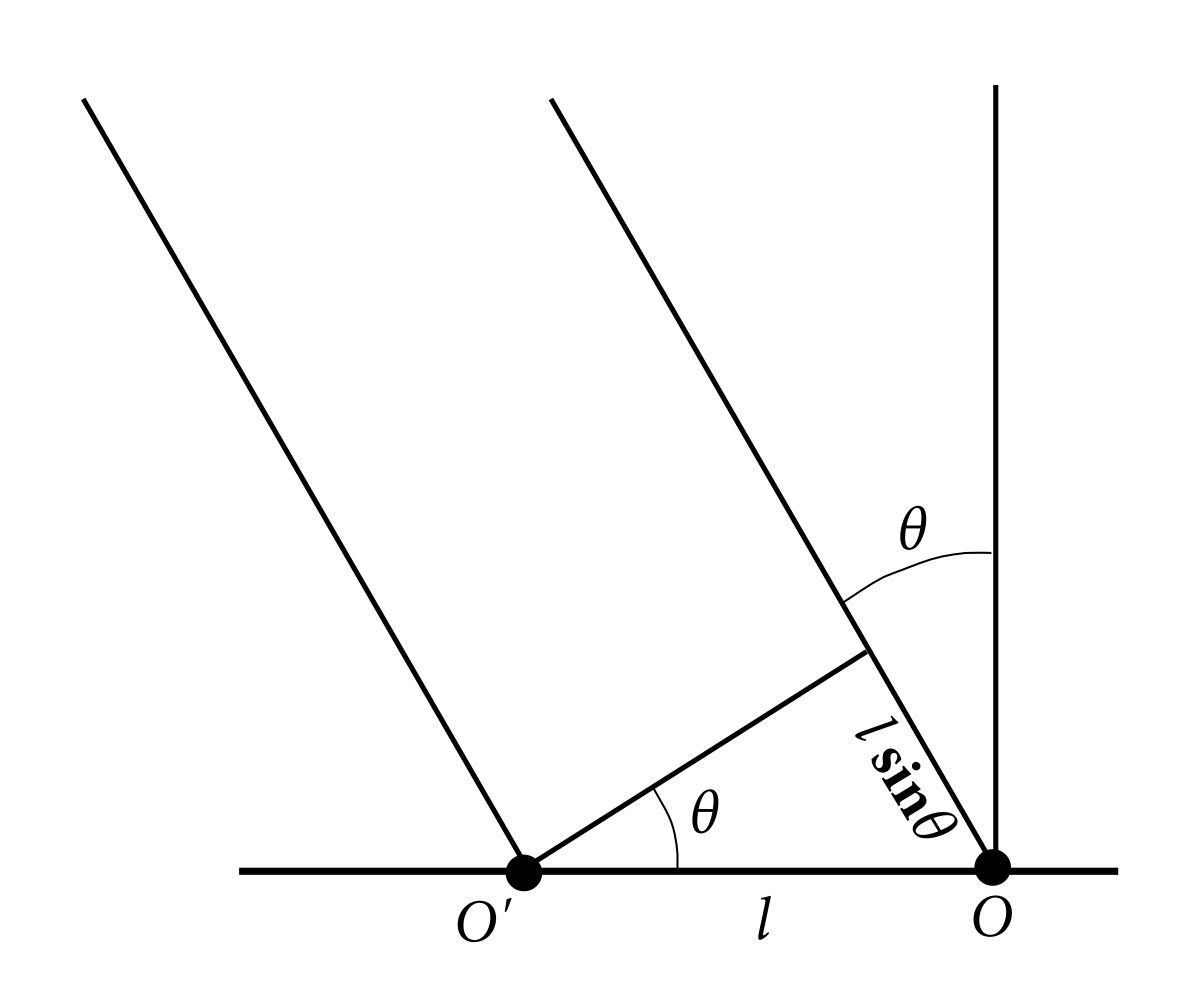
図9.10
O'Aの方が\(l\sin\theta\)だけ短くなる。一方右側に向かう経路は逆に\(l\sin\theta\)だけO'Bの方OBより長くなる。だから点O'から出る光の経路に関しては、右側の方が左側より、\(2l\sin\theta\)だけ長くなる。つまり \[ \text{O'B}-\text{O'A}=2l\sin\theta \] である。そしてACとBCの距離は等しい。だからO'からBを経由してCにつく経路はO'からAを経路を経由した経路より\(2l\sin\theta\)だけ長い。つまり \[ \text{O'BC}-\text{O'AC}=2l\sin\theta \] である。この経路差がおよそ波長程度になると、O'からレンズを通ってCに向かう様々な経路は互いに打ち消し合って、スクリーン上で波の強さが0になるだろう。つまり \[ 2l\sin\theta=\lambda\Longleftrightarrow l=\frac{\lambda}{2\sin\theta} \] ということである。最初に書いたように\(2l\)が分解能となる。つまり \[ \frac{\lambda}{\sin\theta} \] が分解能である。今は測定物がレンズの軸の中心にある場合での話だった。レンズの軸から離れれば、この値も変わるであろうが、今は大雑把な話をしているのでこの程度でいいことにしよう。
尚、このように光路差で波の強弱の場所を求める方法が数学上どの程度の正確さがあるのかは私にはわからないが、物理では通常この方法によって実験に合う結果を得ている。
9.5節 考察
分解能は必ずしも位置の精度とはならない
今の不確定性関係(\ref{p1})を導く議論を振り返るに、分解能というのを位置の精度として使っている。これは光が波であるということから推論されたものである。ところが実際は光は粒子として検出されるのである。だから実は像の広がりというのも、実際はよくよく観察すると図9.11右図のように多数の光子が来たことによるものなのである。今の設定では、光子が一個だけぽ

図9.11
つんとスクリーンに来たということであった。 というのはもし多数の光子が電子に衝突してスクリーンに来たというのならば、運動量の誤差がその分積み重なってしまうからである。今は誤差の最小となる限界を見出そうとして奮闘しているので、それは光子が1つ来たときである。 光子が一つだけスクリーンに来るという状況では、分解能を単純に位置の精度とみなすわけにはいかない。 一体全体、スクリーンンに1つだけの光子が検出されたというだけでどうやって電子の位置と運動量を知るのだろうか。これは、以前荷電粒子のスピンを測定しようとして磁場で分離してスクリーンに衝突させて、その位置からスピンを見出そうとしたのと同じような状況なのである。
ハイゼンベルグは光というものを、運動量に関しては光子として扱い運動量の誤差\(2p\sin\theta\)を導き、位置については光波として扱って位置の誤差\(\lambda/\sin\theta\)を導いているのである。そうする根拠はないのである。逆に運動量に関しては光波として扱い、位置に関しては粒子と扱ってみても全くでたらめとは言えまい。運動量を光波として扱えば、電子の受け取った横方向の運動量は0であり、運動量の誤差は0となる。位置に関しては光子として扱う
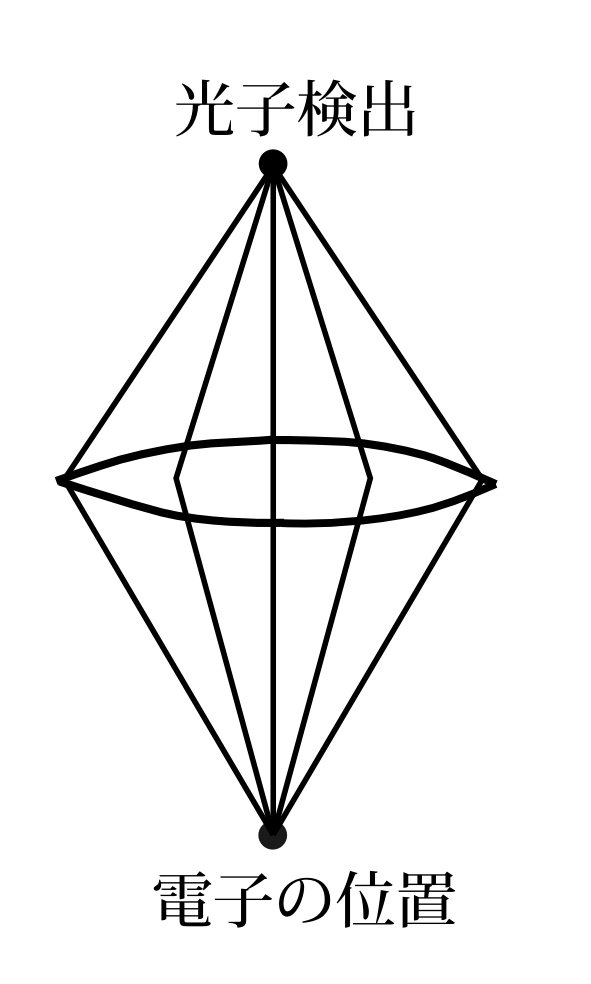
図9.12 光子がレンズの軸上で検出されたとする。光子は図のような様々な経路を通ったはずだが、ある一点に収束する。その収束点が電子の位置であると考えると電子の位置の誤差は0になる。
と、 図9.12の ように幾何光学的に考えて、光子の検出された場所から、多数の経路を逆にたどれば一点にたどり着く。その位置を電子の位置だと決めつければ、電子の位置の誤差は0になる。ハイゼンベルグの理屈が成り立つ――――今述べたように成り立たないのだが――――なら、今の理屈も同様に正当性があるのである。
光波は確率波
さて、この思考実験を量子力学的に扱ってみよう。しかし量子力学で扱えば不確定性定理より、不確定性関係が成り立つことは自明となり、身も蓋もない話になってしまうのだが、一応考えてみようというわけである。光は波として進行し粒子として検出される。当然光度の強いところで多くの光子が検出されるはずであるし、実際の実験でもそうであろう。だから、光波というのは光子の確率振幅だと(量子電磁気学でどうなのかは知らないが)考えられる。光波の強度が光子の存在確率というわけである。
これを前提として議論を進める。電子はまず光を四方八方に散乱する。対物レンズに向かう波もあれば、向かわない波もある。そしてスクリーンで光子が検出され、他の場所では検出されない。これはいわゆる波束の収縮が起きたわけである。ただ光子なら、消滅することもあるので波束の消滅と言ったほうが状況を的確に表しているかもしれない。 これは測定変数が電子と光子の位置の2個の場合である。光子の位置がわかった。電子は光子の位置によって、いろいろな確率振幅を持っていたのだが、光子がある位置で検出されることによってそれに応じた確率振幅が選択される。その確率振幅では電子の位置と運動量はという問題である。 数式で書くと 電子の位置座標を\(\mathbf{r}_e\)、光子の位置座標を\(\mathbf{r}_p\)とすると、この2つを測定変数とした確率振幅 \[ \psi(\mathbf{r}_e,\mathbf{r}_p) \] があり、光子の位置が\(\mathbf{C}\)で検出されたなら、この確率振幅は \[ \psi(\mathbf{r}_e,\mathbf{C}) \] に収縮するはずである。この確率振幅での電子の位置と運動量の確率分布はどうかという問題である。それは不確定性定理から\(\Delta x\Delta p>h\)を満たす。これが量子力学的説明だと思う。
不確定性原理証明の本質
ここで、いろいろな文献――――私の知る限りだが――――に登場する不確定性原理が成り立つという主張のからくりを述べたい。しかしながら、その主張しているところが明瞭でないので、そのからくりを述べると言っても難しいのだが、あくまで私の理解だと思ってもらいたい。
まず、今まで述べてきたハイゼンベルグの顕微鏡についてだが、我々の知覚する現象はスクリーンでの電子から散乱された光の像――――実際は光子なので点だが、今は真実を追求しているのでなく、世間で通用している話に合わしているのである――――である。これから不確定性関係を導いているのであるが、光というのは、常に不確定性関係を満たしているわけである。もちろん、光波の振幅が位置の確率振幅と考え、運動量の確率振幅から、位置の確率振幅への変換行列が\(e^{ip\cdot x/\hbar}\)と言うことは前提としているのだが。だから光はスクリーンで像を作ったときも不確定性関係を満たし、時間を逆にたどれば対物レンズの場所でも、そして電子と散乱したときも不確定性関係を満たしていたわけである(図9.13)。ところで電子と光子の衝突では
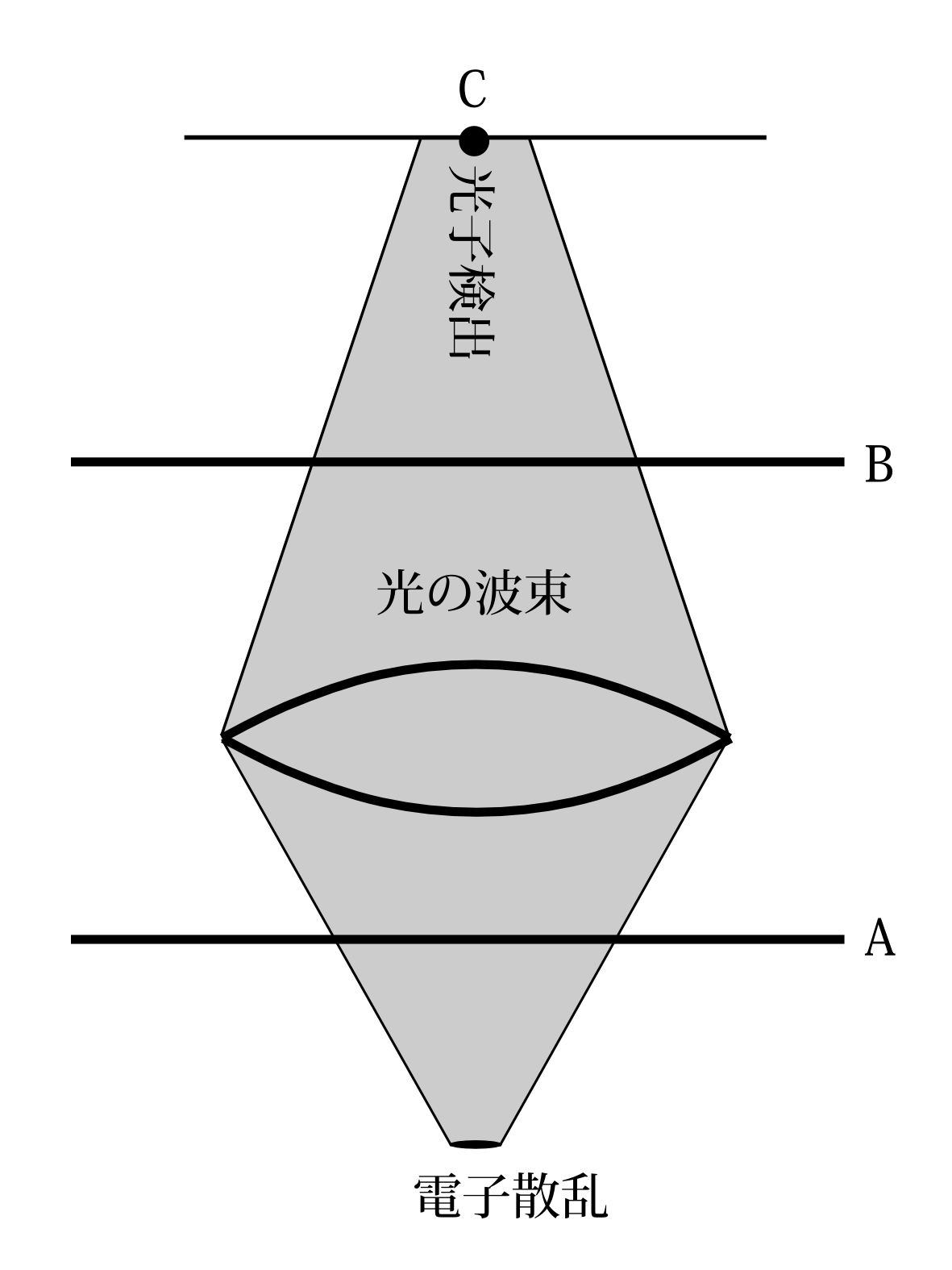
図9.13 光の波束の直線A上でもB上でも不確定性関係\(\Delta x\Delta p>h\)成り立つ。
運動量は保存するとしている。保存するから電子の運動量が推定できるのである。そして電子の位置というのは光と衝突した場所である。となると、電子と衝突後の光が不確定性関係を持っているなら、電子の運動量と位置の精度は光子の精度より良くなることはないわけであり、当然不確定性関係を満たすことになる。
今の論法を見ると、測定器具としての光が常に不確定性関係を満たしながら、被測定物の電子と衝突する。となると、光が顕微鏡の対物レンズを通ったとか、そういうことはどうでもよく、必然的に電子も不確定性関係を満たすことになる。つまり顕微鏡などというたいそうな物など必要なく、論旨というのは簡単に言えば
\(\bullet\) 測定器具は常に不確定性関係を満たしている
\(\bullet\) 測定のためには被測定物は測定器具と衝突しなければならない
\(\bullet\) 衝突の際、運動量は保存し、被測定物の位置は測定器具と衝突した場所である
\(\bullet\) よって、被測定物も不確定性関係を満たす
ということである(図9.14)。 実際のところ、私の知る限りすべての文献
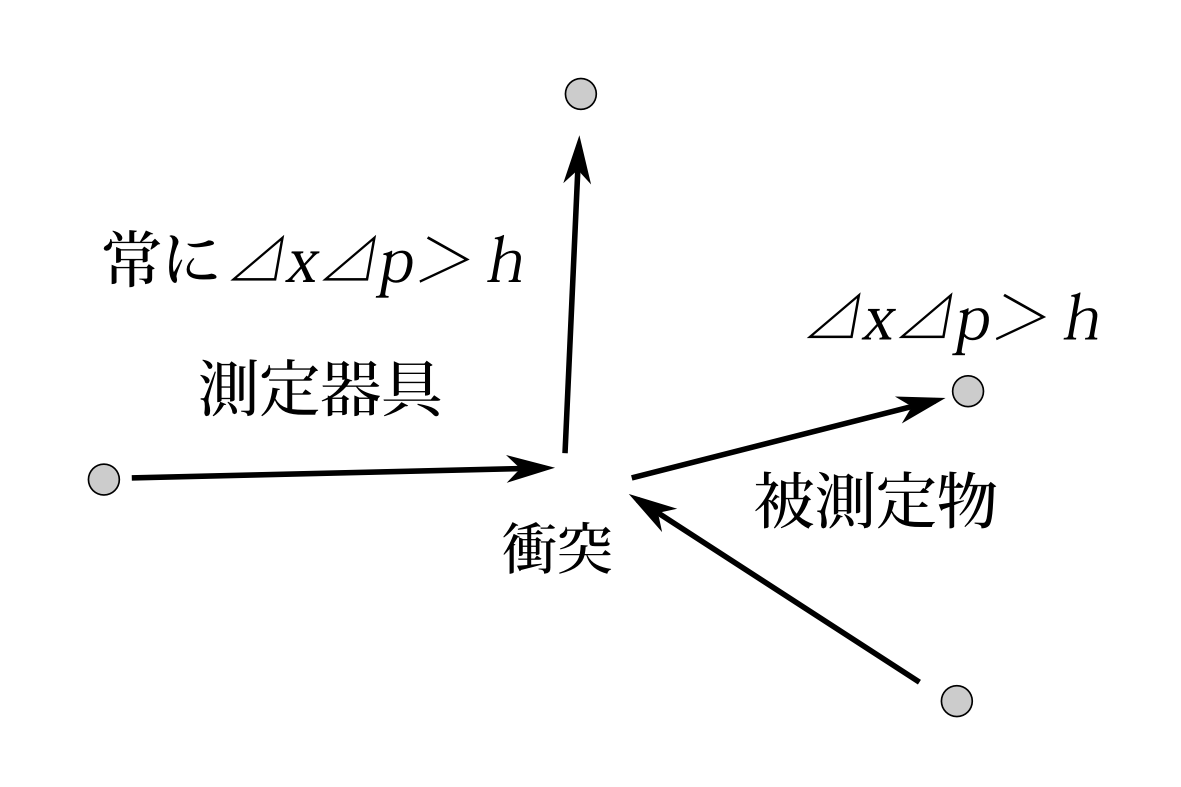
図9.14 模式図。測定器具が不確定性関係を満たしている限り、必然的に被測定物も満たす。
で、測定器具は不確定性関係を満たすということを前提としている。となると被測定物も不確定性関係を満たすのは自明になってしまうのである。これが、最初に私が不確定性原理というのはあまり意味がないと述べた大きな理由の一つである。もちろん測定器具自体の位置と運動量の精度は、測定における重要なポイントである。しかしそれを最初から不確定性関係を満たしているとしてしまっては、不確定性関係の証明としてはあまり意味がないと感じるのである。簡単に言えば測定器具が不確定性関係を満たすなら、被測定物も不確定性関係を満たすということを証明しているのであり、不確定性関係は矛盾がないということなのである。測定器具が不確定性関係を満たすという根拠は位置から運動量への変換行列が\(e^{ip\cdot x/\hbar}\)だからである。思うにこの\(e^{ip\cdot x/\hbar}\)ということを使わずに不確定性関係を証明できなければ不確定性関係が成り立つという証明は意味がないと思う。
9.6節 回析のため断定はできない
ちょっと脱線するが、今まで電子の位置の範囲についていろいろ述べたが、それは単にその範囲内に電子がある確率が高いというだけで、実はもっ
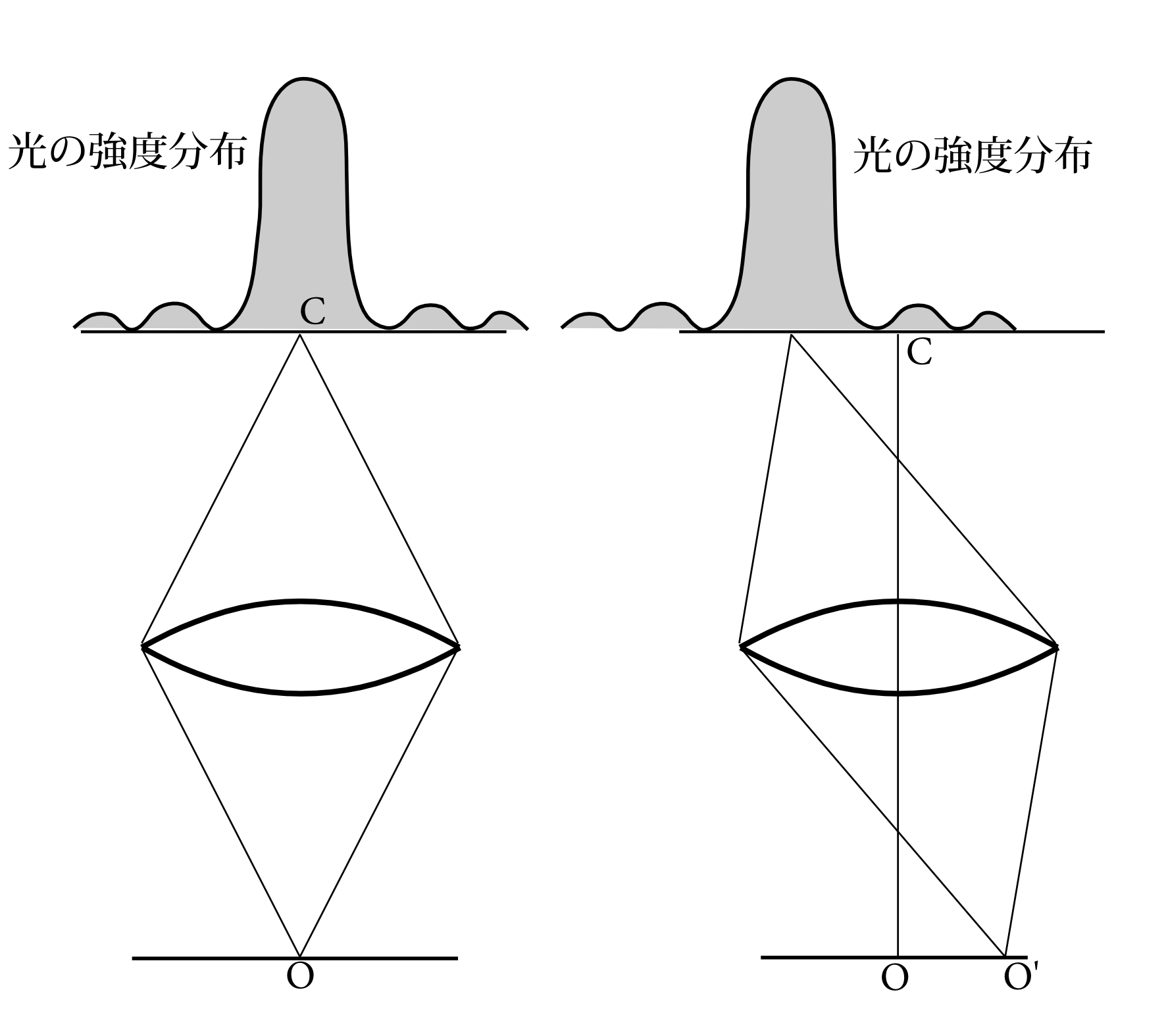
図9.15
と広い。 点Oから出た光はスクリーンで集光するが、その範囲は図9.15左図のような広さを持っているのである。もちろん、ピークのところに圧倒的に強い光が来る(光子が来る確率が高い)が、そこからずれたところにも弱い光が来るのである。これは光が波なので回析するからである。極端なことを言えば、光はどんなところにも回析によってやってくるのである。となると図9.15右図のように、Oからだいぶずれている点O’から散乱された光もわずかながら、Oからきた光が集光する点のピークのCにも光が来るのである。我々はスクリーン上で光子を発見して、それから電子の位置を推測する。その推測された範囲をたとえ分解能の\(\lambda/\sin\theta\)だと考えたとしても、これは単にその範囲にいる確率が高いというだけなのであり、この範囲に100%存在するとは断定できない。その範囲からずっと離れたところに電子がある可能性も決して0ではないのである。6.2節で述べたような、霧箱や光電子倍増管のようなものなら、そこで粒子検出の信号があれば、その装置の中に粒子は100%存在するといえそうである。しかしながら、これはやや極端な言い方だが、霧箱の中の白い線というものも、今の顕微鏡の例のように、ぜんぜん異なる場所から来た光が我々の目に入ったのかもしれないのである。この考え方をあらゆる知覚に当てはめて考えれば
我々が何かを知覚しても、それから確定的な事実は言えない
ということになってしまうのである。
9.7節 まとめ
不確定性定理が成り立つのは位置と運動量の確率振幅の変換行列が\(e^{ipx/\hbar}\)だからであり、それから波数と波束の広がりの関係という数学的事実を使えば導出される。
ハイゼンベルグの顕微鏡による不確定性関係の証明の思考実験の問題点は電子の位置の測定で光を波として扱っていることである。つまり位置の精度を安易に分解能としてしまっている。実際は光は粒子として検出される。ハイゼンベルグは光を、運動量の測定には光子として、位置の測定には光波として扱っているがそうすべき理由は特にない。逆に運動量では光波、位置では光子として扱えば誤差はなくなる。
光波を光子という粒子の確率波として考え、 量子力学の体系でこの顕微鏡を扱うと、光子と電子の2粒子系になる。光子がある点で 検出されたとき、電子の波動関数はいかにという問題となる。しかし光子の検出時に波動関数が何に収縮しようと、これは不確定性定理で述べた理由から、不確定性関係が成り立つに決まっているということになる。
多くの文献での不確定性関係の説明で、測定器自体が不確定性関係を満たしていることを前提としている。測定の際は、被測定物を測定器にぶつけなければならない。測定器が不確定性関係を満たしているなら、衝突の際、それは被測定物に移るのだから被測定物が不確定性関係を満たすのは自明である。それにこれでは不確定性関係を証明しているのではなく、被測定物以外が不確定性関係を満たしているなら、その被測定物も満たさなければならないという証明にしかなっていない。アインシュタインは「不確定性関係が破られる実験装置があるのか」ということでボーアと論争したとのことである。具体的にどのような内容だったかは知らないが、ボーアが測定器具は不確定性関係を満たしているということを前提にすれば、不確定性関係が成り立つのは自明なのであり、「不確定性関係が破られる実験装置があるのか」ということに関してはほとんど意味のない論争だったのだと思う。
ハイゼンベルグの顕微鏡の思考実験を中心に不確定性原理について記述してきた。私はいくつか不確定性関係についての思考実験などを読んだが、意味があると思えるものはなかった。位置と運動量の確率振幅の変換が\(e^{ipx/\hbar}\)であると言う事実を使わずに、不確定性関係を証明できなければ意味がないと思う。変換が\(e^{ipx/\hbar}\)であることは決して自明でもない。これを使わずに不確定性関係が成り立つことを納得させてくれれば、この変換の正しさの証拠にもなろう。しかしながらこのことを使わずに不確定性関係が成り立つことを示すことは無理なのではないかと思う。 とにかく不確定性関係というのは位置と運動量の確率分布がわかれば正しいかどうかわかるのである。しかし、1.10節で述べたように、その肝心の確率分布を実験的に求める方法が無いのである。