第7章 1粒子の物理量の測定
7.1節 測定パターン
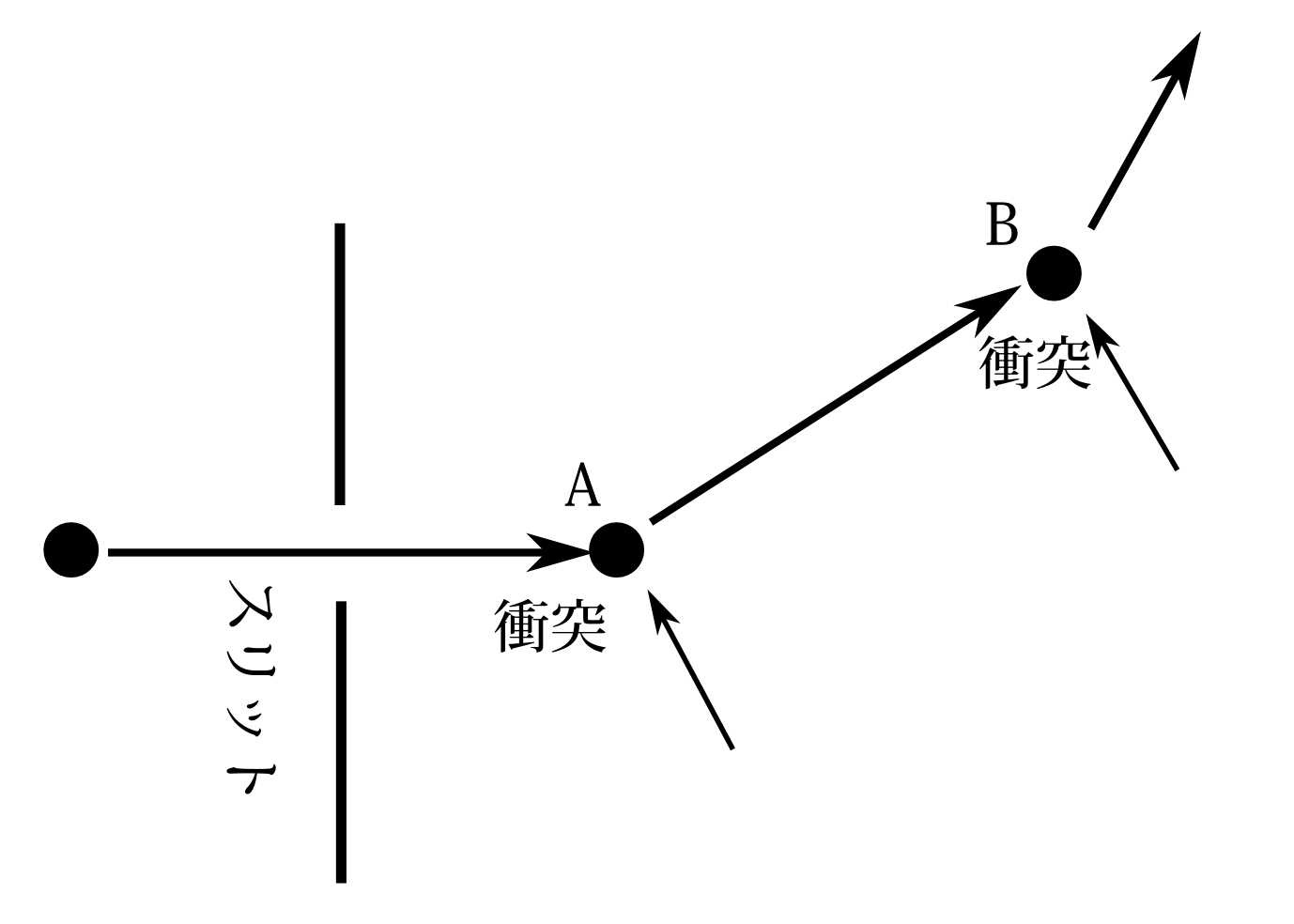
図7.1
1つの粒子の物理量というものをどうやって測ればいいのだろうか。例として、あるスリットから飛び出してくる粒子の運動量を正確に測りたいとする(図7.1)。古典力学では運動量とは速度×質量である。速度を知るためには2つの瞬間での2点間の距離と移動に要した時間を知らなければならない。粒子の位置を知るために、他の粒子を衝突させたとしよう。その衝突の位置Aは正確にわかったとしよう。しかし衝突させると速度が変わってしまう。そして少し時間がたって、また何か別の粒子を衝突を衝突させてその衝突の位置Bがわかったとしよう。ABの距離がわかり、その間の時間もわかれば速度は正確にわかる。しかし我々が知りたいのはスリットを通ったときの速度であり、他の粒子と衝突した後の速度ではない。このように運動量を知ろうと思っても簡単なことではないのである。
一つの粒子の物理量をいったいどうやって測るのだろうか。教科書などには肝心の測定方法というのがあまり出てこないのである。その少ない中から、その本質を抽出すると以下のような測定法になるのだと思う。 それは
- 測定したい運度量やエネルギーなどの物理量の値の大きさごとに、粒子を空間で分離する。
- 分離した粒子の位置を測り、その位置から、その物理量の値を知る。
というものである。2つの粒子を衝突させるにしろ、又、どんな複雑な過程のある実験でも最終的には1つの粒子の物理量を測定しなければならず、必ずこの過程が含まれなければならないのではないだろうか。運動量とスピンを例として考察しよう。
7.2節 運動量、スピンの測定
運動量
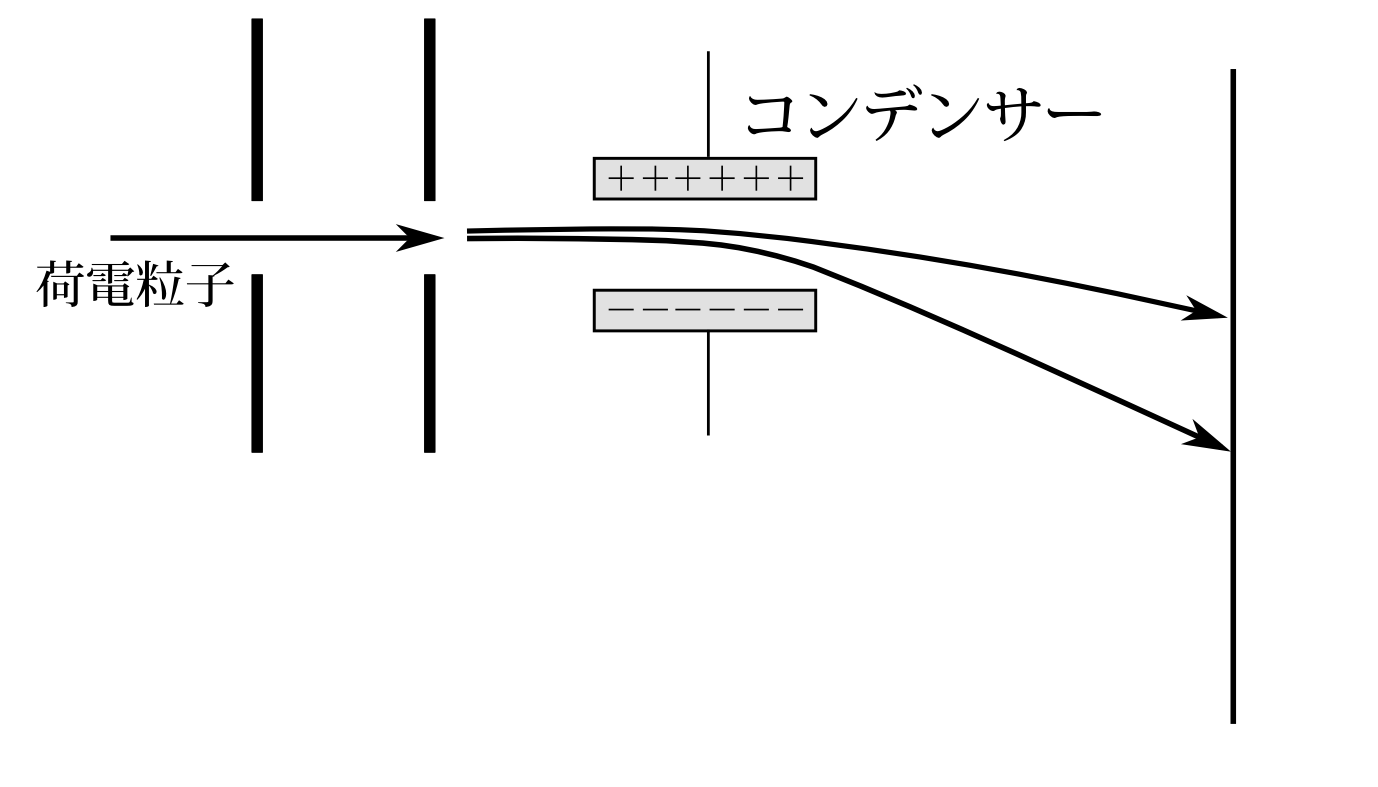
図7.2 荷電粒子に電場をかければ、速度に応じて異なる場所に来る。
スリットを通ったときの荷電粒子の運動量を知りたいとする。その粒子に電場をかけ、スクリーンにぶつける(図7.2)。速度の違いによってぶつかる位置が異なる。速ければあまり曲がらない。遅ければよく曲がる。そのぶつかった位置から古典力学によって軌道を計算し速度を割り出す。これでスリットを通ったときの速度がわかる。同様な測定は磁場で軌道を曲げてもできる(図7.3)。磁場を軌道と直角方向にかければ粒子はローレンツ力を受ける。速ければあまり曲がらず、遅ければよく曲がる。実際、このような方法によって電子の質量と電荷の比を求めたのである。

図7.3 荷電粒子の運動方向に直角に磁場をかければ、速度に応じて異なる場所に来る。
スピン
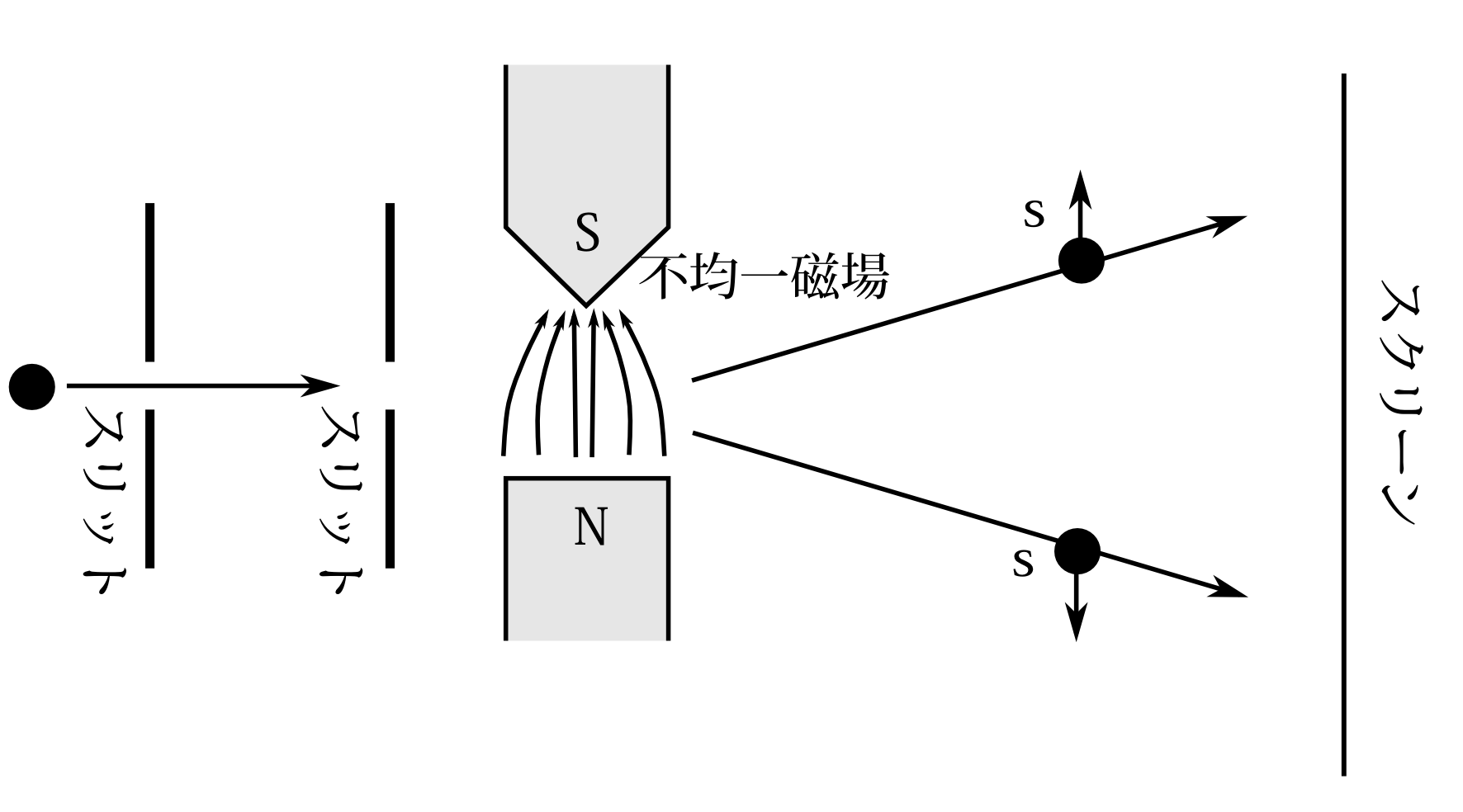
図7.4
スリットを通ったときの粒子のスピンの値を知りたいとする(図7.4)。有名なシュテルンーゲルラッハの実験である。粒子は電荷をもったスピン2分の1の粒子だとする。その粒子を不均一磁場に通す。そして後方のスクリーンにぶつけてその位置からスピンの値を求める。電荷を持ったスピン2分の1の粒子を不均一磁場に通すと粒子は図7.4のように上か下に行く。 古典電磁気学によれば磁気モーメントを持つ物体は不均一磁場で力を受ける。磁石と磁石が引き合うと思ってもらえば良い。スピンが上に向いていると軌道は上に行くように磁石の向きを設定してあるとする。上の地点に粒子が来たら、その粒子は、スリット通過時点でスピンは上向きだったのだと結論する。こうやってスピンが測定できる。
7.3節 スリット通過時に古典論に入るのは正しくない
さて、以上の測定方法では粒子は古典力学に従って運動するとしている。私の知る限りすべての本でこのような説明をしていると思う。しかし粒子はシュレディンガー方程式に従って動くのである。 古典力学に従うとしては誤った結論に導かれてしまう。その理由は2つある。まず、それが明白に分かる例として、トンネル効果について述べよう。
トンネル効果、回析の効果
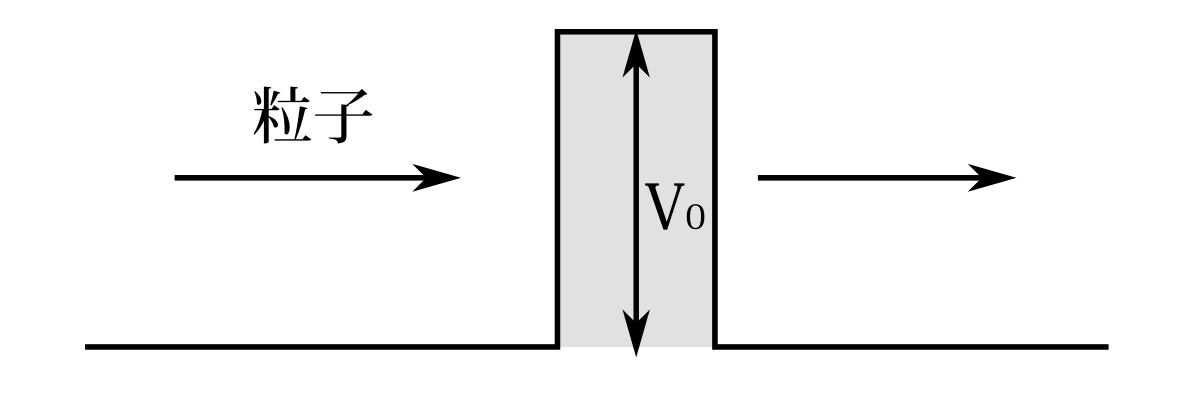
図7.5 トンネル効果の模式図。運動エネルギーがポテンシャルの壁より小さくても通過することもある。
図7.5のように粒子がポテンシャルにぶつかり、そこを乗り越えるか、乗り越えないかで粒子の運動量を測るという実験を考えよう。初等的教科書にも出ていることだが、粒子の運動エネルギーがポテンシャル\(V_0\)より小さくても、粒子はポテンシャルの向こうへ透過しうる。いわゆるトンネル効果である。しかし、もし粒子は古典力学に従うとして、運動量測定にこの装置を使うと、ポテンシャルを通過した粒子は運動エネルギーが\(V_0\)より大きかったと判断してしまうのである。もちろんトンネル効果が起きる確率は小さいのであり、古典力学に従うとしても、大部分の粒子では正しい判断ができるのだが、たまに間違った判断をしてしまうのである。
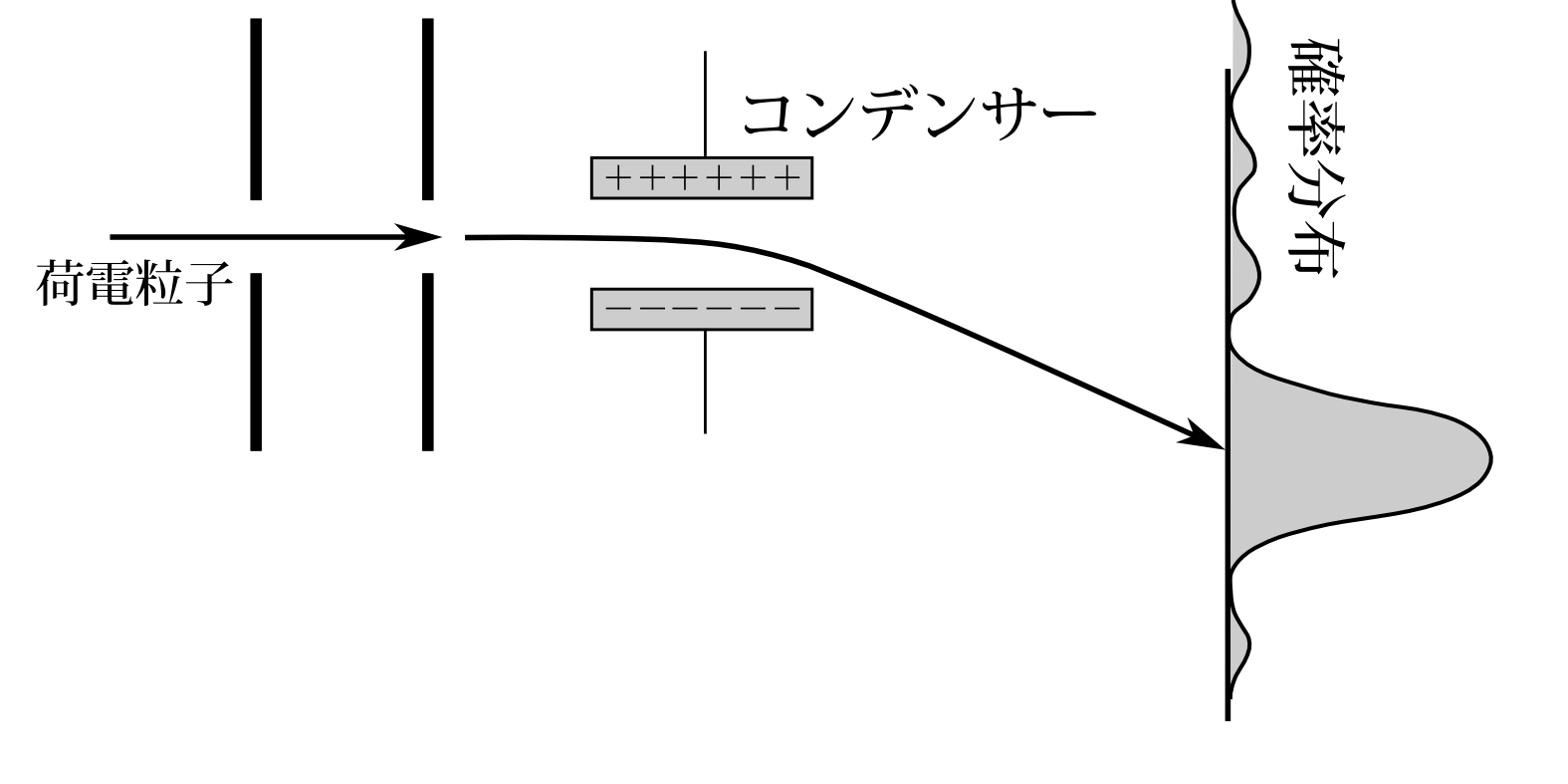
図7.6 ある運動量の測定状態にある粒子のスクリーン上での確率分布。回析のため必ず広がりを持つ。
運動量の例でも運動量のある測定状態にある粒子がスリットを通ったとしても、回析のため粒子のスクリーン上での確率分布は図7.6のようになり、古典力学的には他の運動量の粒子が来るべき位置にもわずかながら行く確率があるのである。 スピンの例でもたとえスピンが下向きに偏った粒子がスリットを通過しても、回析のため、スクリーン上での粒子の確率分布は図7.7のようになり、 上向きのスピンの粒子が来るべき位置にも 僅かながら粒子が行く確率があるのである。
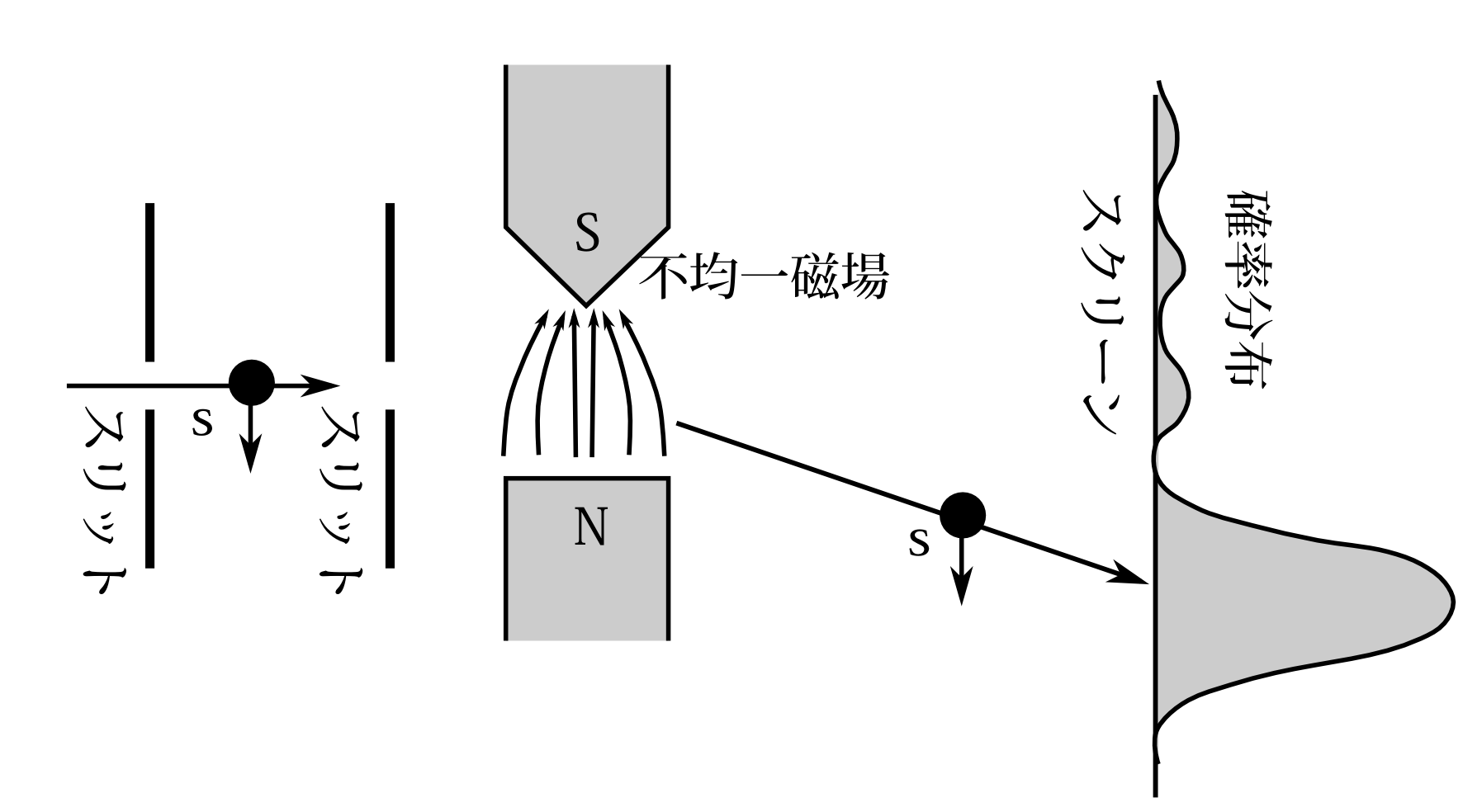
図7.7 スピン下向きの粒子のスクリーン上での確率分布。回析のため広がりを持つ。
ただ第4章、第5章で述べたように、波束内で電場の変化が小さければ、磁場がある場合は波束内で磁場の変化が小さく磁場の空間微分が小さければ、波束の運動は古典軌道に近いので古典軌道で測定結果を推測しても大きく間違わないのだと思う。そこらへんも今から述べる。尚、スピンの波束が古典軌道に従うことについては付録Cで述べてある。
波束が収縮するまではいろんな成分を持っていた
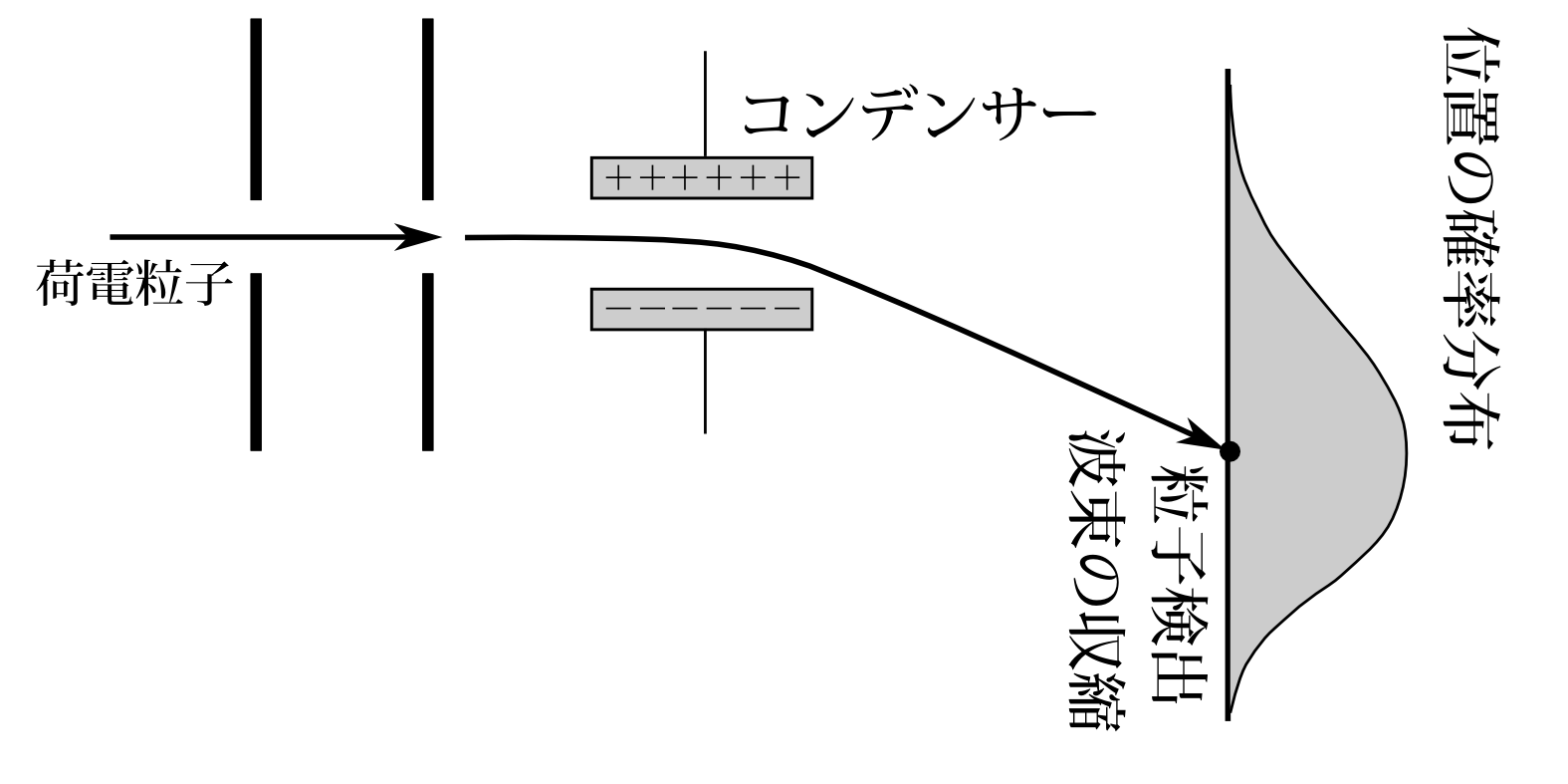
図7.8
スリット通過後古典力学に従って動くと考えると誤った結論に導かれてしまうもう一つの理由を述べよう。スクリーンで粒子が検出されるまでは、粒子の波束は図7.8のように広がっていた。そして粒子が検出されて波束はその点に収縮した。つまり、スリット通過時は、検出位置に対応する運動量を含め、いろんな運動量を持っていたが――これは適切な言い方では無いかもしれないが――波束の収縮で消えたのである。そして前にも述べたように、ある瞬間の物理量とはその確率分布に他ならないと私は考えているので、スリット通過時の運動量を粒子の検出位置からは決して断定できないのである。
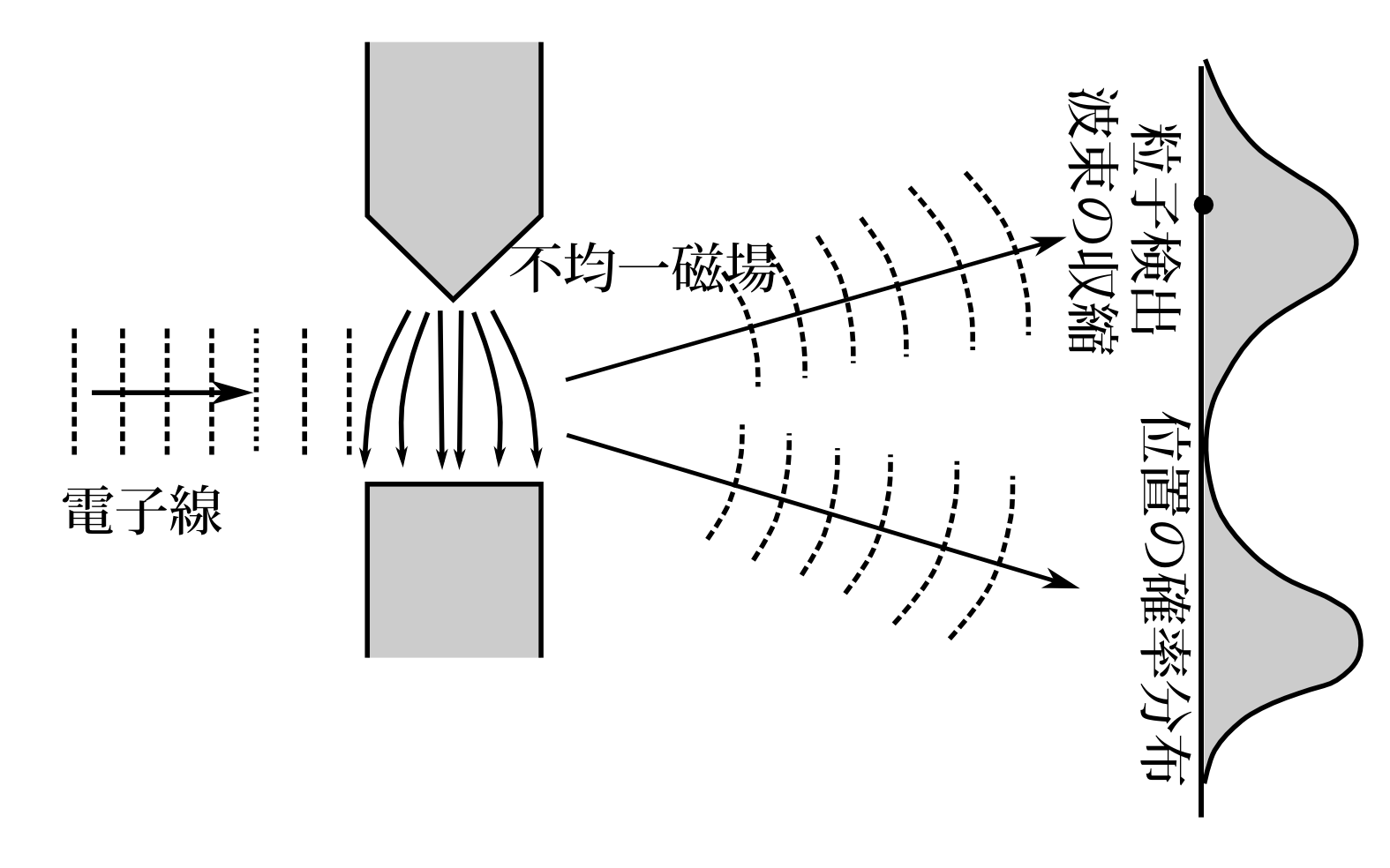
図7.9
スピンでも同様である。たとえ粒子が上の部分で検出されたとしても、図7.9のように、検出される前までは上にも下にも波束があったのであり、それが検出時の波束の収縮で1点に収縮しただけである。波束の収縮で下成分は消えたのである。スリット通過時の波束は上成分も下成分もあった。だから私の解釈では、粒子が上で検出されたとしても、スリット通過時のスピンが上だったとは断定できないのである。
それで、粒子が検出されるまでの過程を量子力学で扱おう。 つまり位置が検出されるまでは \[ i\hbar \frac{d\psi}{dt}=H\psi \] に従って動き、位置が測定されるとその位置に波束が収縮する。どこに収縮するかの確率は位置の確率振幅の絶対値で決まる。トンネル効果や回析の例で古典軌道で扱ってはだめな理由を述べたが、それ以前に、古典力学は正しくないのであって、量子力学で扱うべきなのである。
7.4節検出までを量子力学で扱う(運動量)
まず運動量から分析しよう。 少しまどろっこしいが、順を追って場合分けして考えよう。まず回析を無視できる場合を考え、次に回析を考慮する。おのおのの場合でスリットでの初期状態がわかっている場合とわかっていない場合を考える。もちろん知りたいのは初期状態が未知で回析を考慮する場合である。回析を無視できる場合というのは――回析はどんな系でもあるのだが――無視しても結果にほとんど影響を与えないほど回析が小さい状況だという意味である。
状態がわかっているというのは運動量がわかっている場合と言っていいと思う。これは4.5節でも述べたことである。測定というのは幅があり、運動量を測定するということはある範囲からある範囲に運動量があると言うことを知る行為である。一方状態が既知の場合というのは運動量と位置の確率分布が既知ということであり、運動量がどの範囲にいるのかがわかっている場合である。つまり、既に測定されてしまっている場合だとと考えられるわけである。もちろんこれについては異議もあろうが、ここら辺は言葉の使い方の問題であり、あまり気に留めないでいただきたい。大事なのは何が起きるかということである。
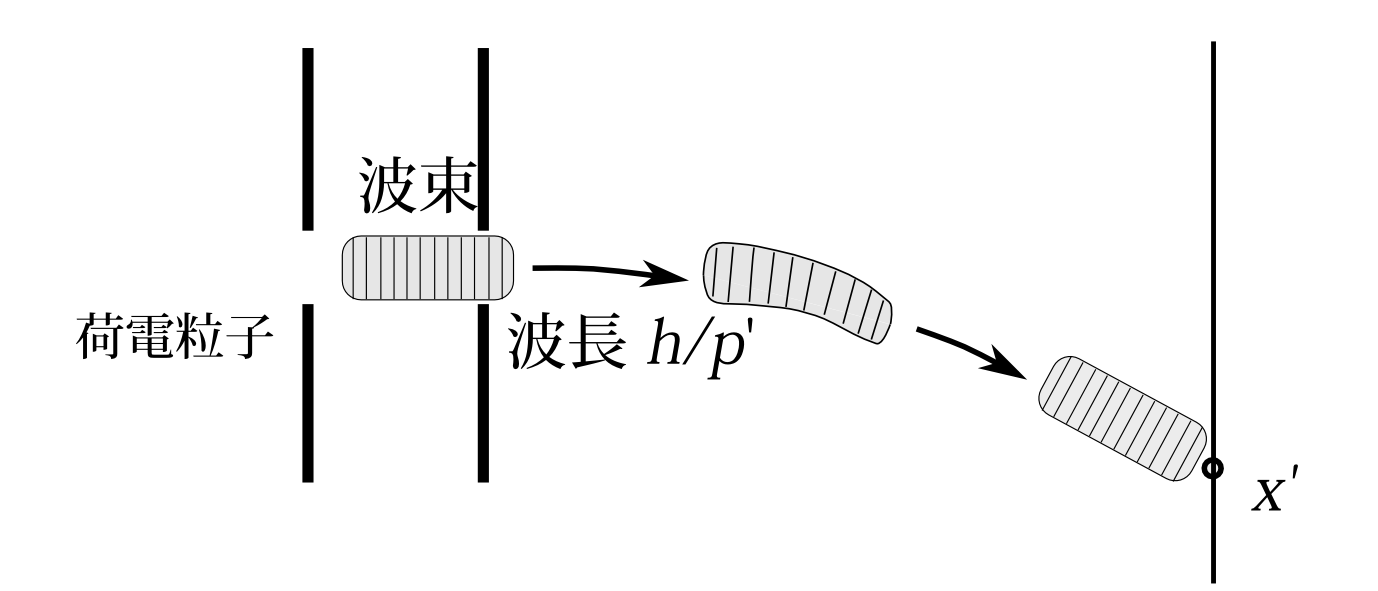
図7.10 波束内の線は波の山を表す。
今粒子はスクリーンの\(x'\)という位置で検出されたとする。この\(x'\)に対応する運動量を\(p'\)とする。対応するというのは、スリットで運動量\(p'\)の測定状態にある粒子はスクリーンで\(x'\)を中心にした確率分布を示すという意味である。 運動量の測定状態にある粒子の位置の確率分布は無限に広がってしまい、こんなことにはならないのだが、これは確率分布が運動量\(p'\)付近のある幅を持った状態だと考えてもらいたい。そうすると波束は図7.10のように、ある範囲内にだいたいおさまり、第4章、第5章で述べたように、その波束は近似的に古典力学の方程式に従って動く。だからこの\(p'\)というのは古典力学の方程式に従えば、\(x'\)の位置に到達するはずの運動量といっても――全く同じではないであろうがここではそういうことを議論したいわけではないので――いいと思う。
回析は無視、初期状態既知
まず、回析が無視でき、 スリットを通過するときの量子力学的状態がわかっている場合を考える。その運動量表示の確率振幅を\(\varphi(p)\)とすると、スリットでの運動量確率分布は単に\(|\varphi(p)|^2\)というだけであり、運動量はわかっているということである。
スクリーンで検出されたときの運動量はどうか。スリット通過のとき、運動量表示で\(\varphi(p)\)という確率振幅を持っていて、位置\(x'\)で粒子が検出された。 状態は位置表示で \[ \delta(x-x') \] に収縮し運動量の確率分布はすべての運動量の値で同じ値になる。簡単に言えば、運動量の値は全くわからなくなってしまうということである。実際は測定に幅があるのでデルタ関数には収縮しないが、位置の確率振幅が幅のあるデルタ関数に似たものに収束するにせよ、運動量が0を中心にどの方向も均等に分布するかというと決してそうでなく、霧箱の例(6.2節)では検出前の運動量の向きを保持している。しかしそういうことを考えても、分析のしようがないので形式的な量子力学の法則に従ってデルタ関数に収束するとして話を進める。この結果を模式的に書くと図7.11のようになる。
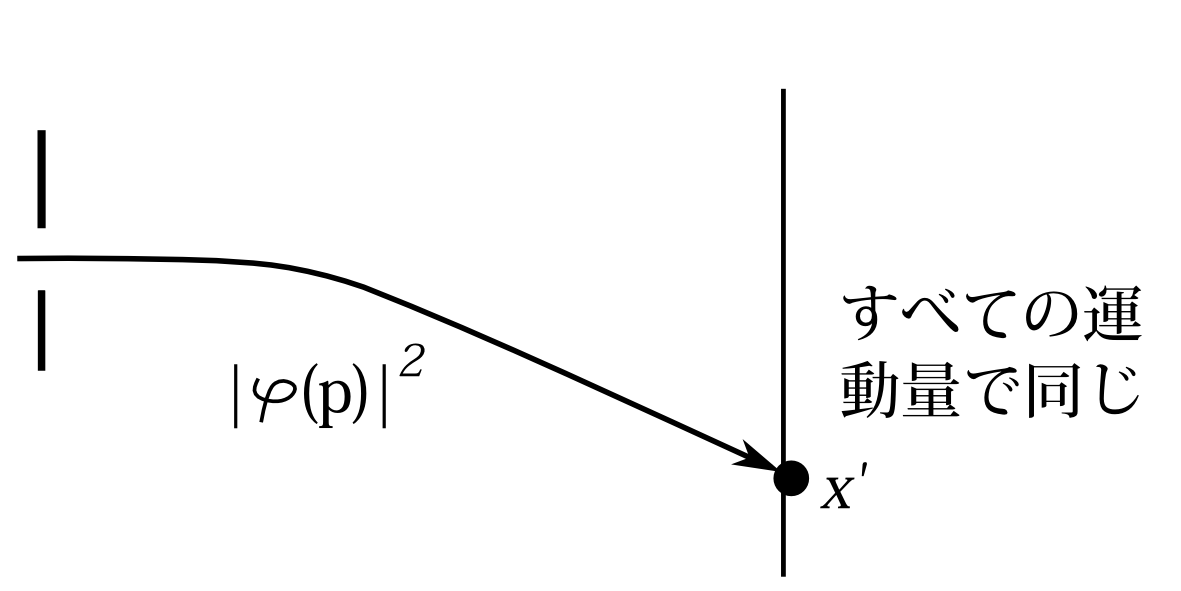
図7.11 回析は無視。初期状態\(\varphi(p)\)は既知
回析は無視、初期状態未知
次に回析が無視でき、初期状態が未知の場合を考える。初期状態が未知と言ってもなんらかの量子状態にあるはずである。 状態を知らないというのは、ただ単に観察者が知らないだけで、他の人は知っているという場合もある。今の場合はそういう場合でなく、状態を知るための痕跡を自然界に残していないという場合である。 さて、位置\(x'\)で検出されれば\(\delta(x-x')\)に収縮するのは前と同様である。だからスクリーン上での運動量の確率分布はすべての運動量の値で同じ値になる。今は回析は無視できるほど小さいというのだから、位置\(x'\)成分に対応する運動量\(p'\)成分を持っていなければ位置 \(x'\)で粒子が検出されることはない。だからスリット通過時には、少なくとも運動量\(p'\)の成分をもっていたはずだとは言える。だから初期状態の運動量の確率振幅\(\varphi(p)\)は未知だが、少なくとも\(\varphi(p')\ne 0\)であることは言える。この結果を模式的に書くと図7.12のようになる。しかし粒子が1つだけ来ただけでは\(\varphi(p')\)の大きさがどれほどなのかは何とも言えない。
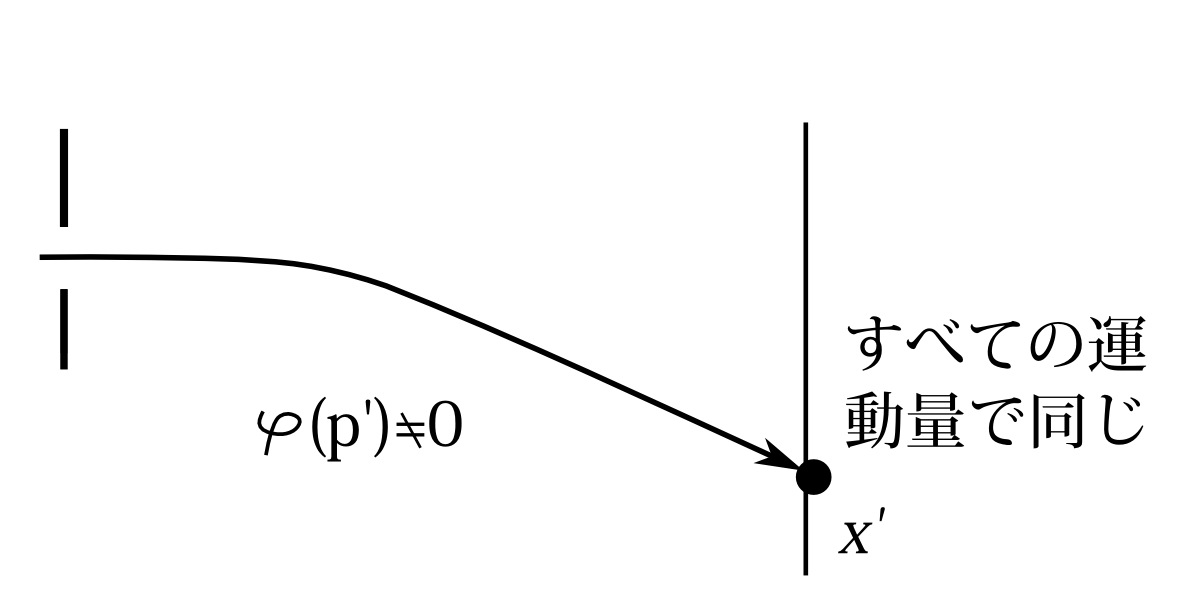
図7.12 回析は無視。初期状態\(\varphi(p)\)は未知
回析考慮、初期状態既知
さてこれからは回析を考慮する。まず初期状態が既知の場合だが、このときもスリットでの運動量確率分布は\(|\varphi(p)|^2\)であることは同じであり、スクリーンで\(\delta(x-x')\)に収縮するのだから運動量の確率分布はすべての運動量の値で同じ値になる。この結果を模式的に書くと図7.13のようになる。
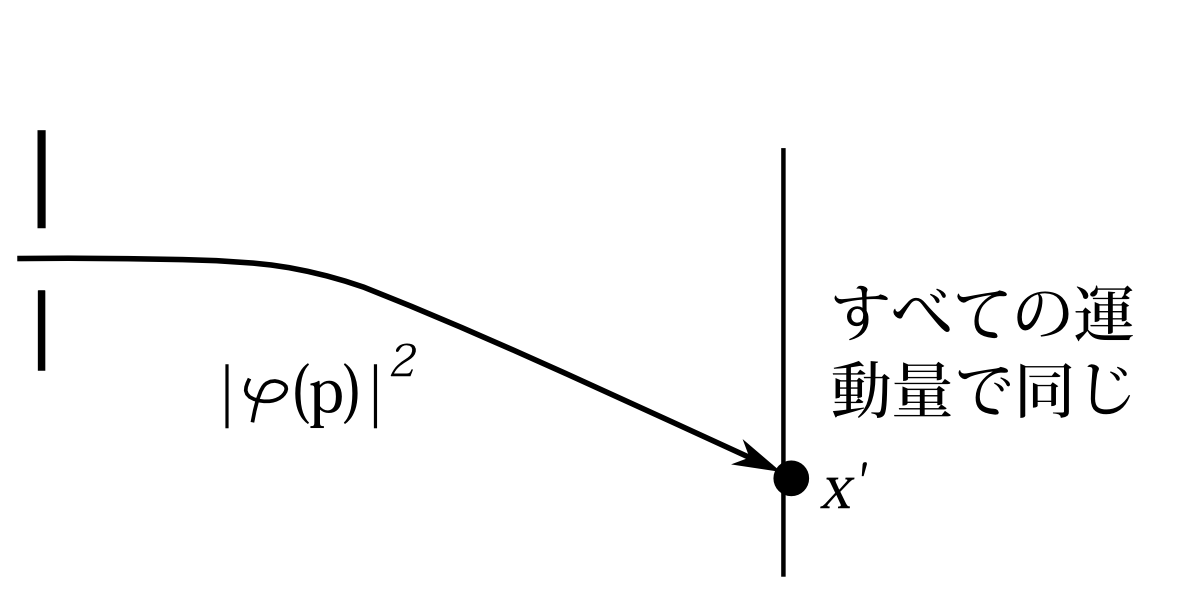
図7.13 回析を考慮。初期状態\(\varphi(p)\)は既知
回析を考慮、初期状態未知
次に初期状態が未知の場合を考える。初期状態がわかっているなら測定する必要はないのだから、この場合こそ運動量を測定したい場合である。この場合もスクリーン上での運動量の確率分布はすべての運動量の値で同じ値になる。 回析を考慮すると位置\(x'\)で検出されたからと言って、初期状態で\(x'\)に対応する運動量\(p'\)の成分を持っていたとは言えない。というのは例えばスリット通過時に、\(p'\)と異なる運動量の測定状態にある粒子でも、回析のため\(x'\)に来ることはありうるからである。しかしながら回析が起きる割合というのは非常に小さい。というより回析があまり起こらないように装置をセットしているはずである。だから初期状態の運動量の確率振幅\(\varphi(p)\)は未知だが、おそらくは\(p'\)成分をもっていたであろうと推測できる。つまり、\(\varphi(p')\ne 0\)である可能性は高いとは言える。しかし回析が大きければその可能性もその分低くなる。そして\(\varphi(p')\)の大きさについては何もわからな
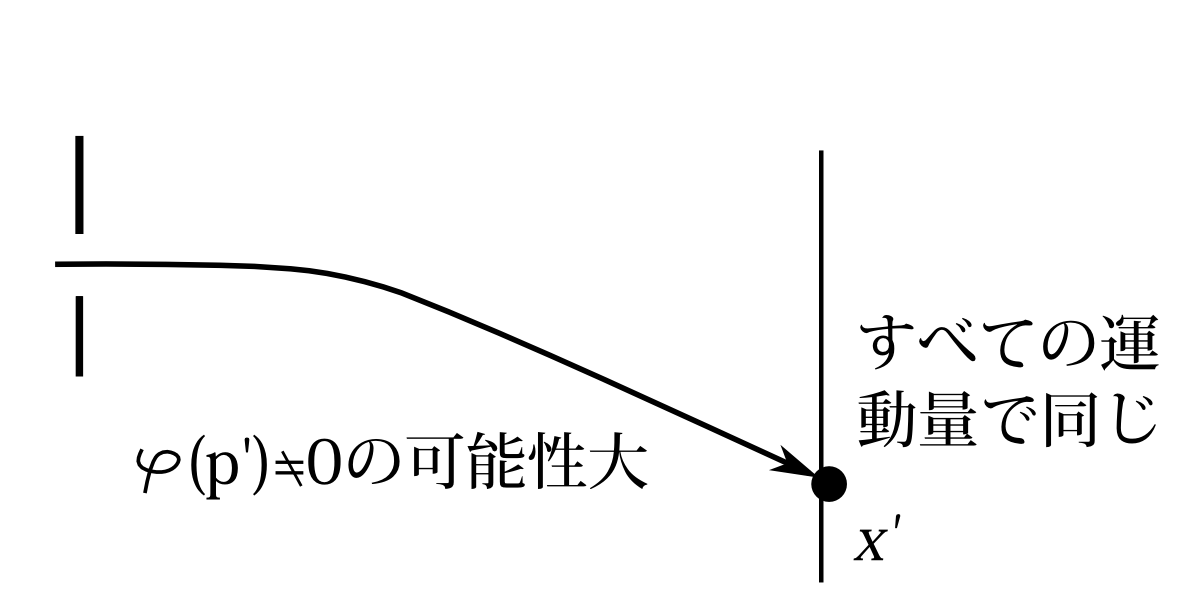
図7.14 回析を考慮。初期状態\(\varphi(p)\)は未知
い。この結果を模式的に書くと図7.14のようになる。この位置\(x'\)に対応する運動量がとんでもない高エネルギーで、室温の実験ではありえないような状況であれば、\(p'\)成分があったとは推測せず、回析のためだろうと考えるであろう。だから、\(\varphi(p')\ne 0\)の可能性が高いという推論するにあたって、\(p'\)成分を含んでいる可能性はそれなりにあったということがもともとの前提としてあるのである。今、スリット通過時の状態は未知だとしているが、実は何もわからないのではなく、実験室の温度などからある程度、運動量の状態についての知識があるわけである。ここらへんの状態が未知、既知というのもよくわからない領域である。
結論
以上の分析結果を表にすると以下のようになる。
| 分析法、状況 | スリットでの運動量 | スクリーンでの検出後の運動量 |
|---|---|---|
| 回析無視、\(\varphi(p)\)既知 | \(|\varphi(p)|^2\) | すべての運動量で同じ |
| 回析無視、\(\varphi(p)\)未知 | \(\varphi(p')\ne 0\) | すべての運動量で同じ |
| 回析考慮、\(\varphi(p)\)既知 | \(|\varphi(p)|^2\) | すべての運動量で同じ |
| 回析考慮、\(\varphi(p)\)未知 | \( \varphi(p')\ne\) 0の可能性大 | すべての運動量で同じ |
| スリットから古典論 | \(p'\) | 不明 |
最後の段には粒子がスリットから古典軌道を通ってスクリーンに衝突するとしての結果も加えた。軌道を量子力学的に扱った測定結果というのは、回析を考慮して、初期状態が未知の場合である下から2段目のものである。 スリットでの運動量は古典軌道を通ると考えた場合は\(p'\)であり、量子状態で考えた場合ではせいぜい\(p'\)の確率振幅を持つ可能性が大きいとしか言えない。粒子が1つだけ検出された場合はこの程度のことしか結論は出せないのだと思う。正しいのはもちろん粒子検出までを量子力学の時間発展方程式で扱った方であるが、量子論では運動量の定義が明確でないのでスリットでの運動量と言ってもあまり意味がないと思う。それよりも、科学とは我々が知覚可能なものの関係なのだから。何が起きるか、どこで粒子が検出されるかが大事なことだと思う。
考察
スリットでの運動量は、古典軌道を通ると考えた場合は\(p'\)だと断定し、一方、量子力学的に扱った場合では――回析を無視したとしても――\(p'\)を含めたいろんな成分があったという。この二つにどういう違いがあるのだろうか。我々に知覚可能な違いがあるのだろうか。
さて、今、この測定される粒子と相互作用する粒子を含めた確率振幅で考えてみよう。相互作用している粒子というのは、磁石を構成している粒子であったり、スリットを構成している粒子であったり、スクリーンを構成している粒子であったりする。その多数ある粒子の位置変数を一つの文字\(x_外\)で代表することにする。そして測定される粒子がスクリーンで検出される直前の確率振幅を \[ \psi(x,x_外) \] だとする。これは\(x\)の値をパラメータとして\(x_外\)についての確率振幅があると考えることができる。粒子が\(x'\)で検出されたことにより、確率振幅は \[ \psi(x',x_外) \] に収縮するが、\(x_外\)についての確率振幅としてこれが選ばれたわけである。現実に起きたことはただこれだけのことである。古典軌道論で考えた場合のスリットで運動量\(p'\)であったなどとは決して言えない。しかしながら場合によってはこの確率振幅が選択されたことによって運動量が\(p'\)であったと考えてもよさそうな場合もあるかもしれない。これは運動量の保存ということを使うのだが、そのことを運動量の場合で説明するのは難しいので、スピンの場合(7.7節)で説明する。
私は
今ここを通った粒子の運動量を測ってくれと言われても測りようがない
と思う。 では確率振幅が\(\varphi(p)\)の状態にあるというのはいったい何を意味しているのだろうか。測りようがないのに、\(|\varphi(p)|^2\)が確率分布だと言っても意味がないではないか。これは難しい質問だが――そしてそんな疑問が湧くこと自体が量子力学の欠陥なのだろうが――これを位置の確率振幅に変換したものが位置の正しい確率分布を与えるというのが、その意味するところだと思う。それなら、その確率振幅\(\varphi(p)\)は運動量とは何の関係もないではないかと思われるかもしれない。私もそう思うがあえて関係づけるとすれば、第4章、第5章で見たように、運動量\(p\)付近の波の重ね合わせの波束(位置の確率分布)はそれに対応する速度\(p/m\)で 動くのである。
測定というものはどこかで古典論の世界に入らなければならない。軌道の運動を量子論で扱ったと言っても粒子の検出では古典力学的に扱わなければならない。量子力学のままでは確率振幅のままであり、現象が現れないからである。ただ、これはいいすぎかもしれない。波束の運動は決定論であり、現象と言えるかもしれない。おそらく、なるべく過程の後の段階まで量子論で通したほうがより正確な結果がえられるのではないだろうか。
7.5節多くの粒子で実験する場合
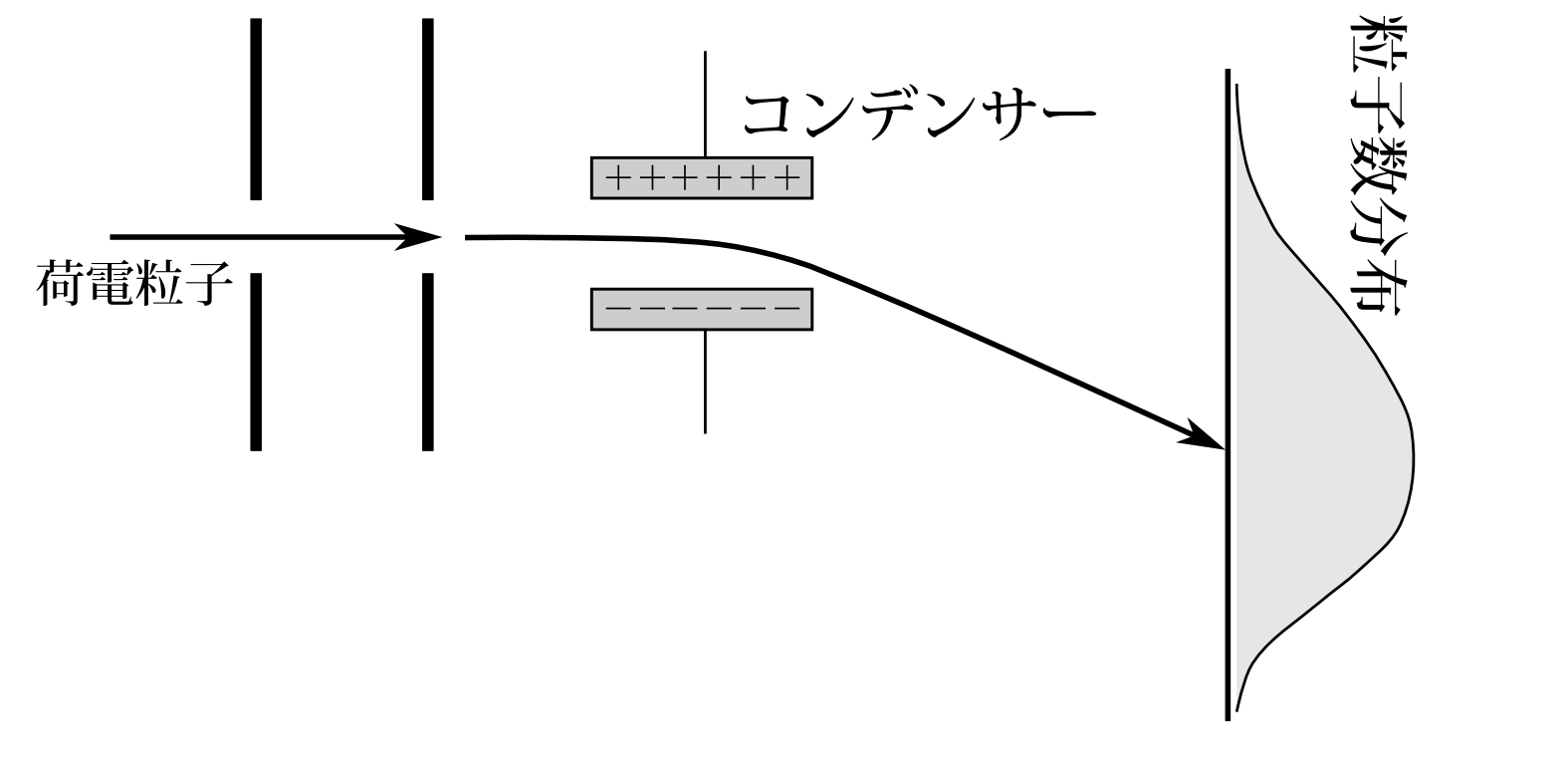
図7.15
今は粒子が1つだけ来た場合であったが、実際の実験では膨大な数の粒子が飛来する場合を扱うであろう。今粒子が多数来て、スクリーン上で図7.15のような粒子数分布が得られたとしよう。そして、実験はある一定時間続くわけだが、我々の知りうる限り同じ状況で実験をしたとする。そうなると次にくる粒子のスリット通過時の状態は、 運動量の確率分布がその粒子数分布に対応したものが来ると予想していいのではないだろうか。だから、例えば、粒子数分布が図7.16のように、すべての粒子がほぼ同一の点にばかり来るなら、次に来る粒子のスリット通過時の状態はその点に対応する運動量の測定状態になっていると予想できる。私が言いたいのは、量子力学では初期状態をいかにして知るかという問題があるが、このように同一の実験を繰り返せば初期状態が予想できるということである。
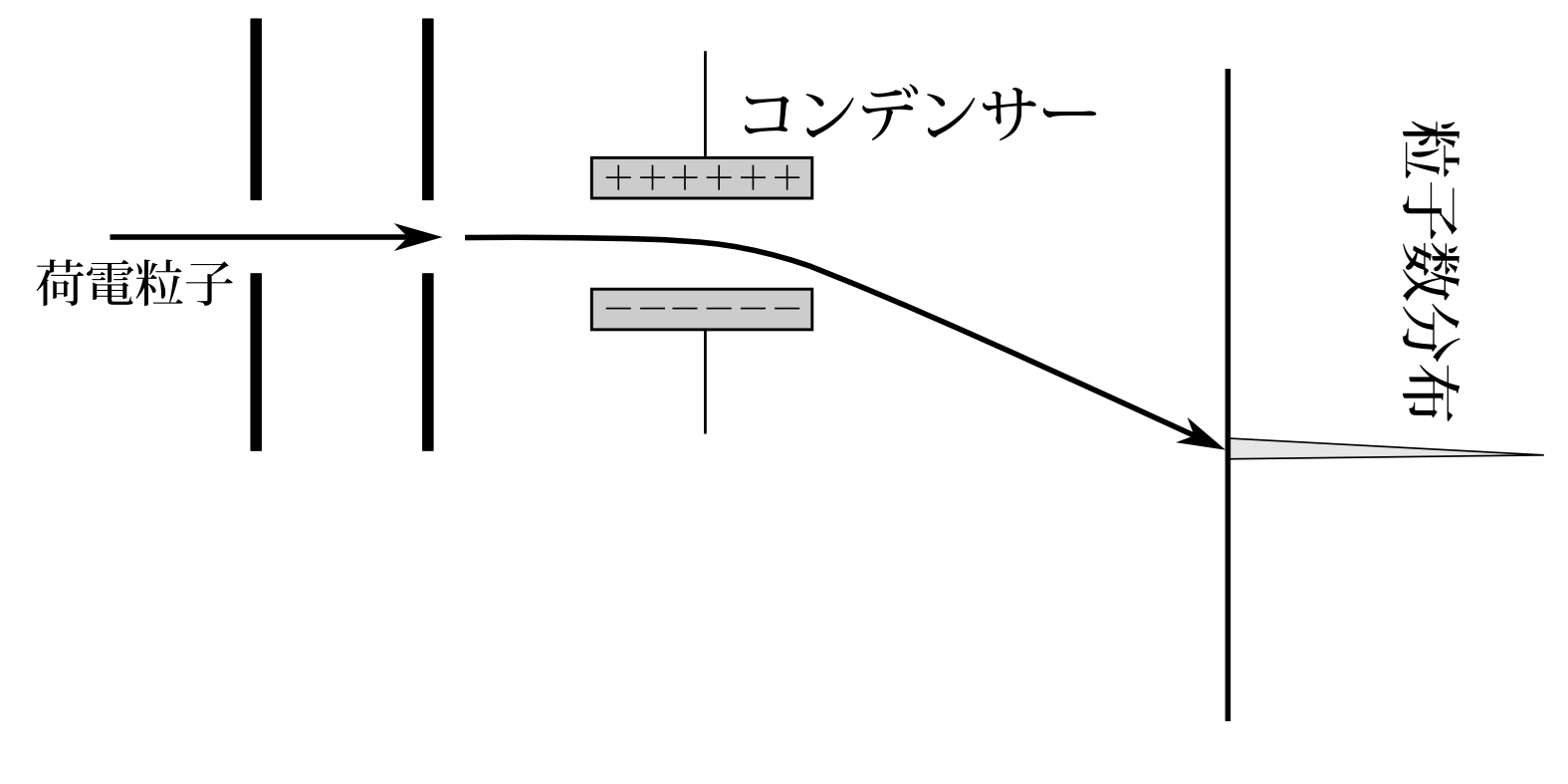
図7.16
さて、もしスクリーン上の位置\(x'\)に粒子がアボガドロ数程度来たら、\(x'\)でスクリーンの受け取った運動量はどの程度となるだろうか。私は、その位置に対応する運動量\(p'\)にその粒子数を掛けたものになると思う。それは古典力学は粒子数の多いとき、回析を無視できるときにはおおむね正しいからである。となると\(x'\)に来た粒子の運動量はスリット通過時に運動量\(p'\)を持っていたと考えても良さそうである。ただ量子力学の枠組みではそういう結論は導き出せない。そういう結論に持っていくには量子力学を超えた解釈が必要である。
1つの粒子がスクリーンで検出されてもスリットでの運動量については何も言えないに等しいが、 同じ状況で膨大な粒子がスクリーンで検出される場合、
・ スリットでの状態の推定が可能
・ スクリーンが受け取る運動量がわかる
のだと思う。
7.6節 運動量測定状態への収縮
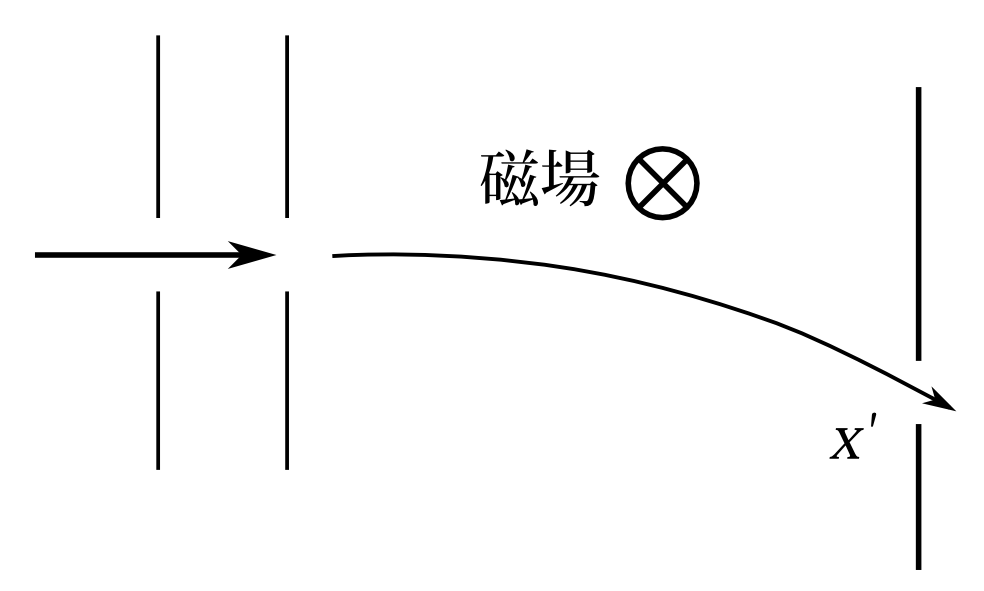
図7.17
今の実験と関連して、運動量の測定状態というものを作ることができるか考えたい。 今、\(x'\)に穴を開けて波が通れるようにする(図7.17)。 波の一部は\(x'\)を通ることになろう。この\(x'\)を通った波だけ見れば運動量の測定状態となるだろうが、実際はこれは波の一部であり、他の部分は残っている。粒子がスクリーンに衝突するはずの時間になってもスクリーンで粒子が検出されなかったら粒子は\(x'\)を通ったはずだとわかる。となると波は\(x'\)を通った波束のみとなり、他は消える。これは運動量の測定状態と言えなくもない。しかしながら粒子が1つだけ最初のスリットを通ったと、どうやって知ることができるのだろうか。そのことを確かめるためには最初のスリットの
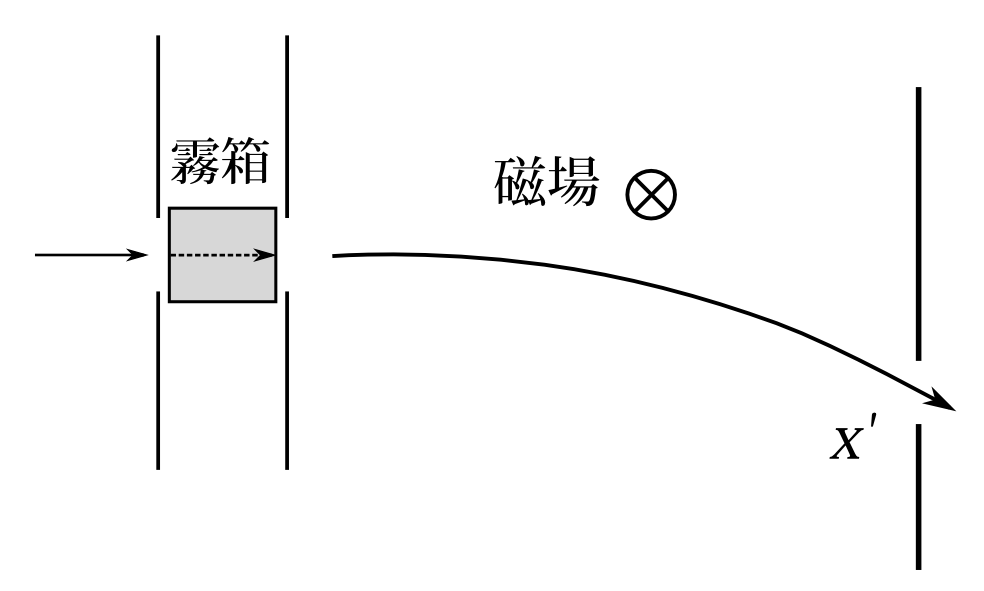
図7.18
ところに霧箱を置いてみるとよい。霧箱で軌跡が見られる(図7.18)。 そして粒子が霧箱を通過した後いつまでたってもスクリーンに来なければ、\(x'\)を通ったとは言える。しかし、そのためにはいつまで待てばよいのだろうか。常識的には霧箱の軌跡から速度を概算して、およその着く時間はわかる。だからほぼ100%の確率で\(x'\)を通ったとは言える。だからその常識的な時間待てば、\(x'\)を運動量測定状態の単色波が通ったとは言えそうである。だから運動量測定状態への波束の収縮はあるとは思う。 ただ、これは、与えられた状況で、例えばスリットを通った粒子の運動量を知りたいというような状況で、運動量を測って、その結果運動量の測定状態に収縮したわけではない。運動量の測定状態を作り出しているのである。もちろんこれでも\(x'\)を通り抜けた粒子の運動量はわかるわけだから測定したと言えばそうとも言えるが、与えられたものを測っているのではないことには注意。 又、今の場合も\(x'\)を通った波にも回析した成分が入ってくるので完全な運動量測定状態ではない。尚、この分離して一部を通すという方法は他の物理量例えばスピンの場合などにも適用できる。
古典軌道論と量子軌道論での予測の一致

図7.19
さて、図7.19のように、この\(x'\)を通った波を再び電場や磁場で曲げ、スクリーンで粒子を検出するとしよう。\(x'\)を通った粒子は、回析の効果を無視すれば、運動量\(p'\)の測定状態にあるわけだから、その運動量に応じた点、それを\(x''\)とするが、で検出されるはずである。さて、一方間違いだと切り捨てた最初のスリットを通ったときから古典力学で扱うとすると、粒子はどこで検出されると予測することになるだろうか。このときも\(x'\)を通った粒子は運動量\(p'\)だというのだから、粒子は\(x''\)で検出されると結論される。量子論で扱った場合は、最初のスリットを通った時点ではいろんな範囲の運動量を持っていたと結論される。一方、古典軌道論ではその時点で運動量は\(p'\)だったと結論する。しかし、粒子検出という我々の知覚できる現象に対しては同じ結論に達するのである。そういう意味で運動量というものも定義次第だと考えるわけである。ただ古典軌道論は、回析というものが考慮されないので、回析を考慮すれば粒子検出まで量子論で扱ったほうがより現実に合うはずである。
さて、今の実験を分析するにあたって重要なことを述べていると思う。\(x'\)を通った粒子の運動量はおよそ\(p'\)とわかっていても位置については運動方向の前後の幅は全くわからない。状態は運動量と位置の確率分布で定まるのだから、状態については大雑把にしかわかっていないということである。しかし、\(x''\)で検出されるという未来が予測できるのである。だから
初期状態がそれほど正確にわからなくてもわれわれの鈍い知覚では十分役立つほどの予測はできる
のである。
7.7節 検出までを量子力学で扱う(スピン)
次にスピンを粒子検出まで量子力学の方程式で扱う。運動量のときと同じように分析するが、状態は位置\(x\)とスピン\(s\)の2つの測定変数の確率振幅\(\psi(x,s)\)で表されるので少しややこしい。運動量のときとの違いは測定変数が2つに別れていて、その一方を測定し、他方を推定するということである。スピン変数\(s\)は上向きと下向きの2つの測定値のみである。運動方程式は \[ i\hbar \frac{d}{dt}\psi=-\frac{\hbar^2}{2m}\triangle \psi-\frac{q}{mc}\mathbf{B}\cdot \mathbf{s}\;\psi \] である。時間発展方程式がこうなる理由は付録Bで検討する。この方程式によって図7.20のようにスピンの上向き成分\(\psi(x,上)\)は磁場によって上の方
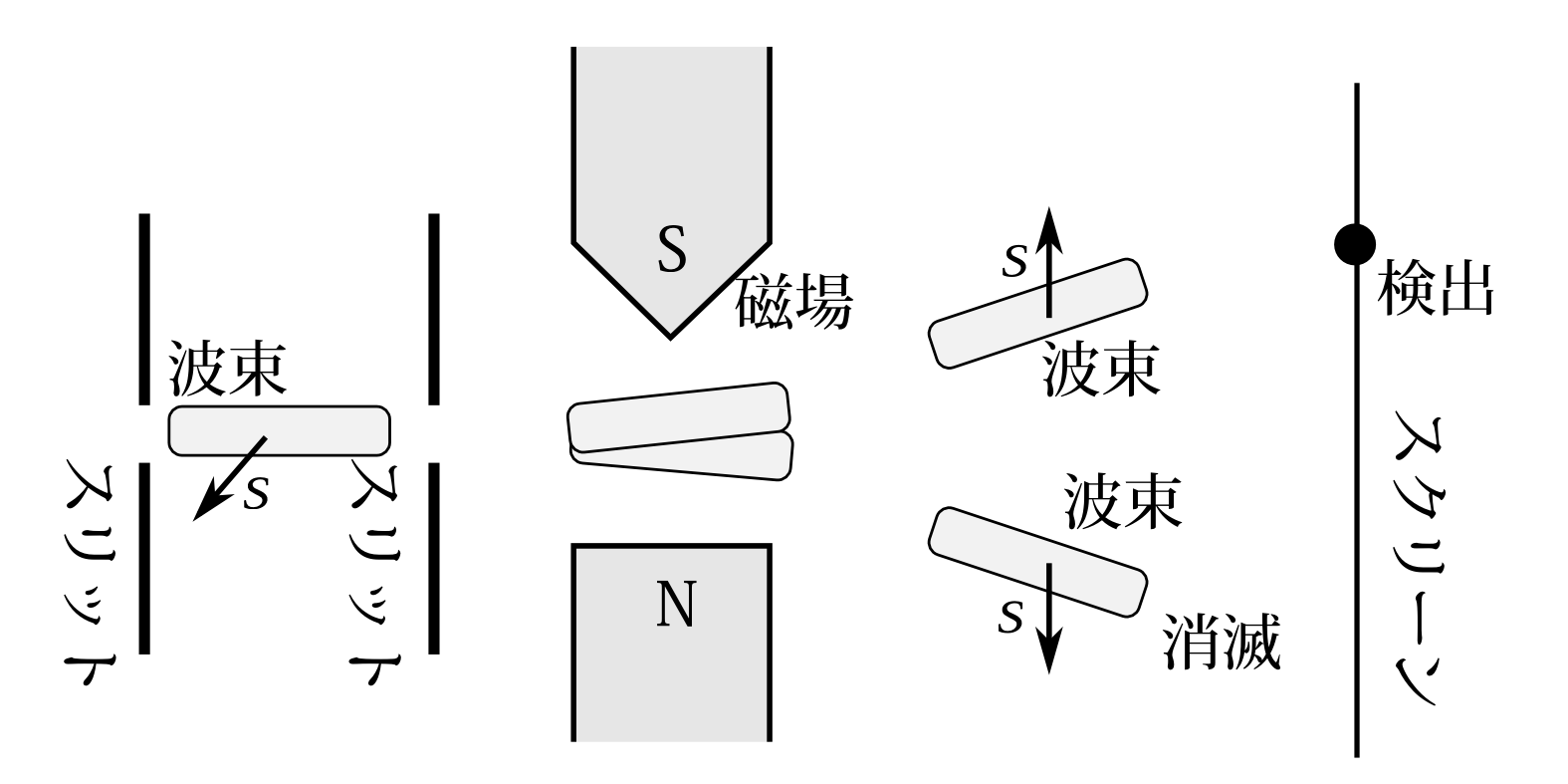
図7.20
向に曲げられ、下向き成分の\(\psi(x,下)\)は下の方向に曲げられる。つまり上向きの波束は古典電磁気学での上向きの角運動量を持った粒子の軌道とだいたい同じ動きをする。下向きの波束は古典電磁気学での下向きの角運動量を持った粒子の軌道とだいたい同じ動きをする。そうなることの数学的な説明は付録Cを見て欲しい。
今粒子はスクリーンの\(x'\)で検出されたとする。その位置は古典電磁気学では上向きスピンの粒子が来るべき位置であり、量子力学ではスピンが上向きの波束が来るところとする。 運動量の分析をしたときのように回析を無視する場合と考慮する場合、おのおのの場合について初期状態が既知の場合と未知の場合に分けて考える。
回析無視、初期状態既知
まず、回析を無視して、スリットを通過するときの確率振幅\(\psi(x,s)\)がわかっている場合を考える。スリットでの位置\(x\)でのスピン\(s\)の確率分布は\(|\psi(x,s)|^2\)であり、運動量のときと同様、これが測定値とも言える。スクリーンでの位置\(x'\)で検出されると、これは測定変数の一部の測定であり、1.9節で述べたように \[ \psi_終(x',s) \] に収縮すると考えられる。ここで\(\psi_終(x,s)\)というのはスクリーンでの粒子検出直前の確率振幅とする。以下もその意味で使う。今は回析は無いとしているので\(\psi_終(x',下)=0\)である。だからスクリーンではスピンは上向きであると言える。この結果を模式的に書くと図7.21のようになる。もちろん
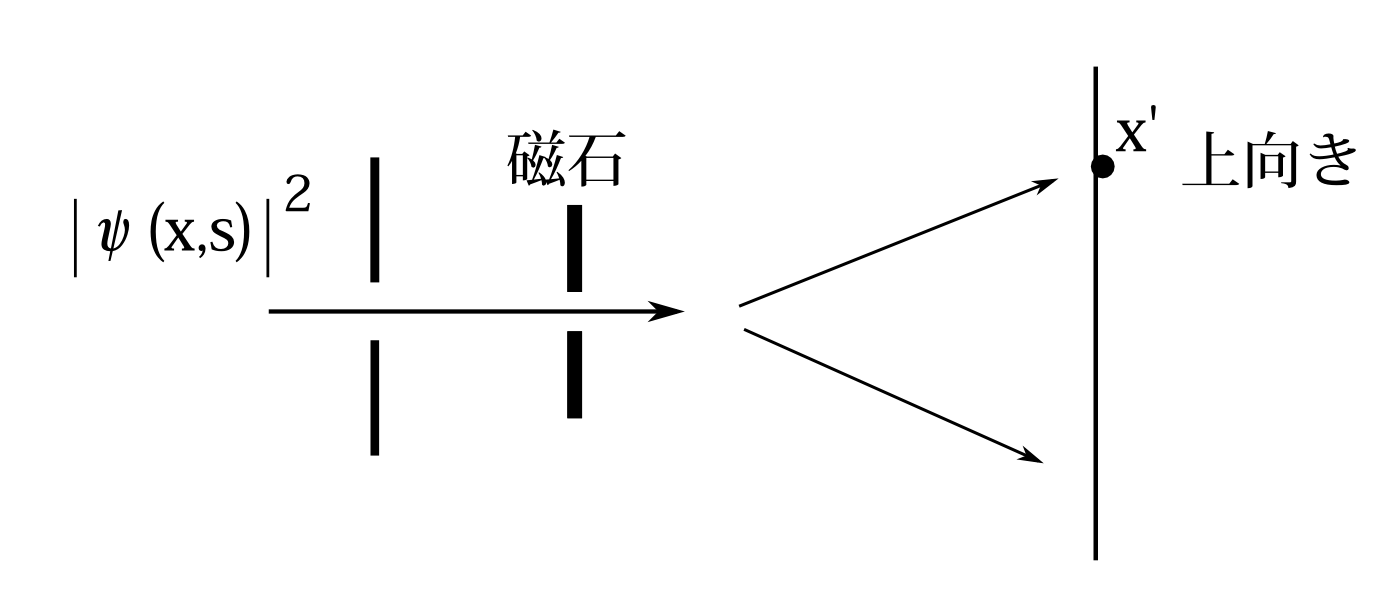
図7.21 回析無視、初期状態\(\psi(x,s)\)既知
スクリーンで検出されたときスピンも影響を受けるはずであり、\(\psi_終(x',s)\)に収縮するとは言えまい。しかしそういうことを考慮しだすと何も言えなくなってしまうので、 そういうことが起きない理想的な実験をしているとして スクリーンではスピンは上向きだとしておく。ここが運動量測定のときとの違いである。
回析無視、初期状態未知
次に初期状態が未知の場合を考える。初期状態が未知と言っても何らかの量子状態にあるはずであり、それが\(\psi(x,s)\)だったとする。スクリーン上の\(x'\)で検出されたとき、状態は\(\psi_終(x',s)\)に収束する。今は回析が無いとしているので\(\psi_終(x',下)=0\)である。だからスクリーンではスピンは上向きだと言える。\(x'\)で検出されたという事実から、初期状態では上向きの成分が0ではなかったとは言える。つまり\(\psi_(x,上)\)がすべての\(x\)で0と言うことはなかったとは言える。もし0だったら回析は無いとしているのだから\(x'\)で検出されることはないからである。この結果を模式的に書くと図7.22のようになる。
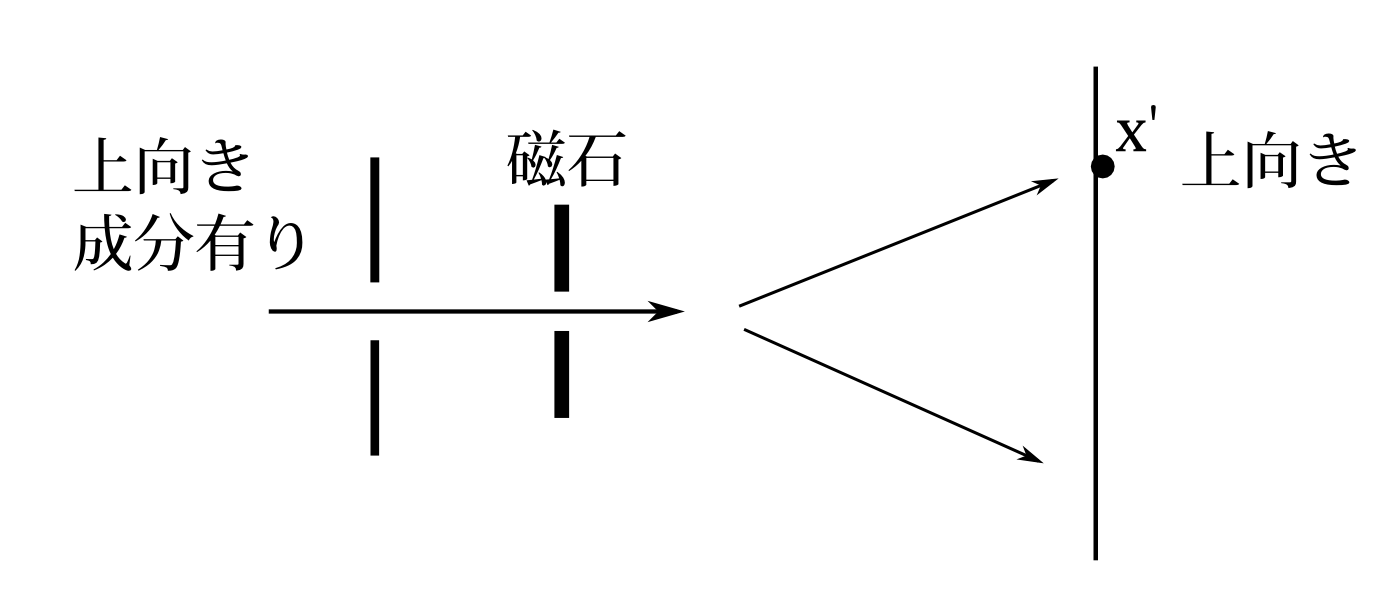
図7.22 回析無視、初期状態\(\psi(x,s)\)未知
回析考慮、初期状態既知
さて、これからは回析を考慮に入れる。このときもスリットでの位置\(x\)でのスピンの確率分布は\(|\psi(x,s)|^2\)であることは回析を無視した場合と同じである。スクリーンでは\(\psi_終(x',s)\)に収縮するのは同じだが、回析によりスピン下向きの成分が来たのかもしれない。だからスピンが上向きとは断定できない。単にスクリーン上ではスピンの確率分布は\(|\psi_終(x',s)|^2\)だとしか言えない。尚、これは規格化されていない確率分布である。この結果を模式的に書くと図7.23のようになる。
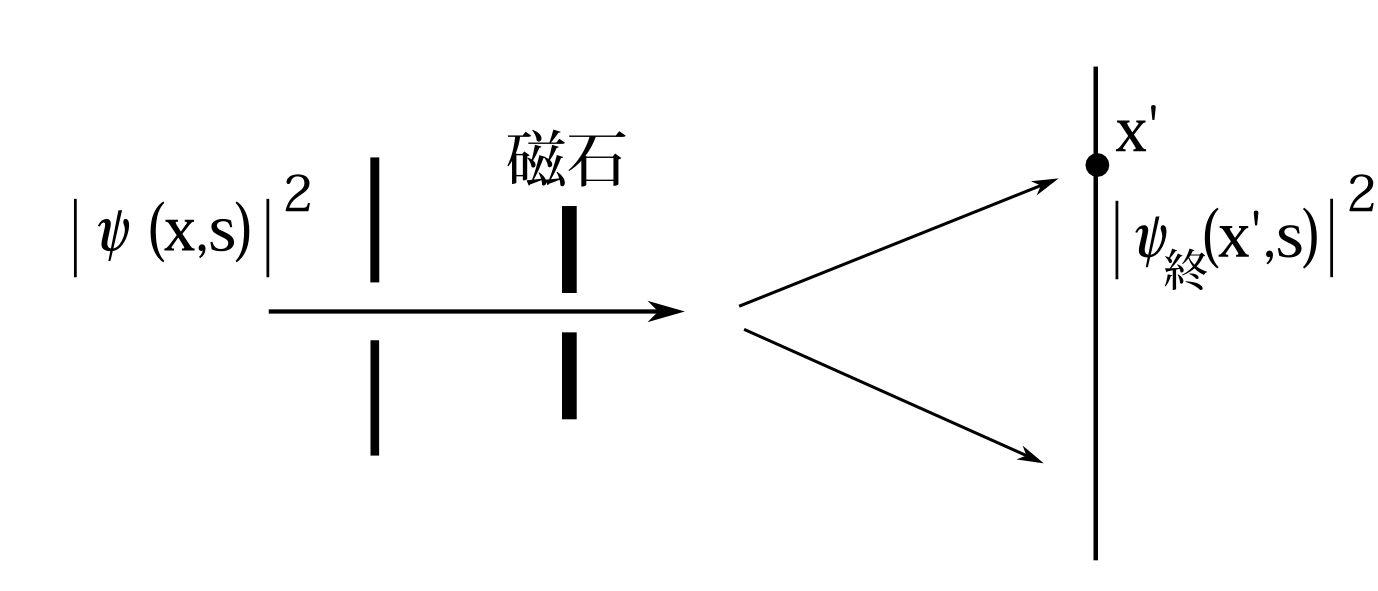
図7.23 回析考慮、初期状態\(\psi(x,s)\)既知
回析考慮、初期状態未知
次に初期状態が未知の場合を考える。この状況こそ――初期状態がわかっているならスピンを測定する必要はないのだから――スピンを測定したい状況なのである。この場合もスクリーン上でのスピンは上向きだとは言えない。初期状態でスピンが完全に下向きに偏っていたもの、つまり上向き成分が無いものが回析によって\(x'\)に来たのかもしれないからである。しかし初期状態がそういうふうに偏っているという情報がないなら――初期状態未知というのはそういう情報がないということであろう――そして回析の割合が小さいように装置が設定してあるなら(通常はしてあると思う)、スピンが上向きの可能性が大きいとは言える。スリット通過時については、同じ理由で、スピンの上向き成分を、大きさはわからないが、持っていた可能性が大きいとは言える。ただ完全に下向きに偏っていたものでも\(x'\)に来る可能性はあるので断定はできない。この結果を模式的に書くと図7.24のようになる。
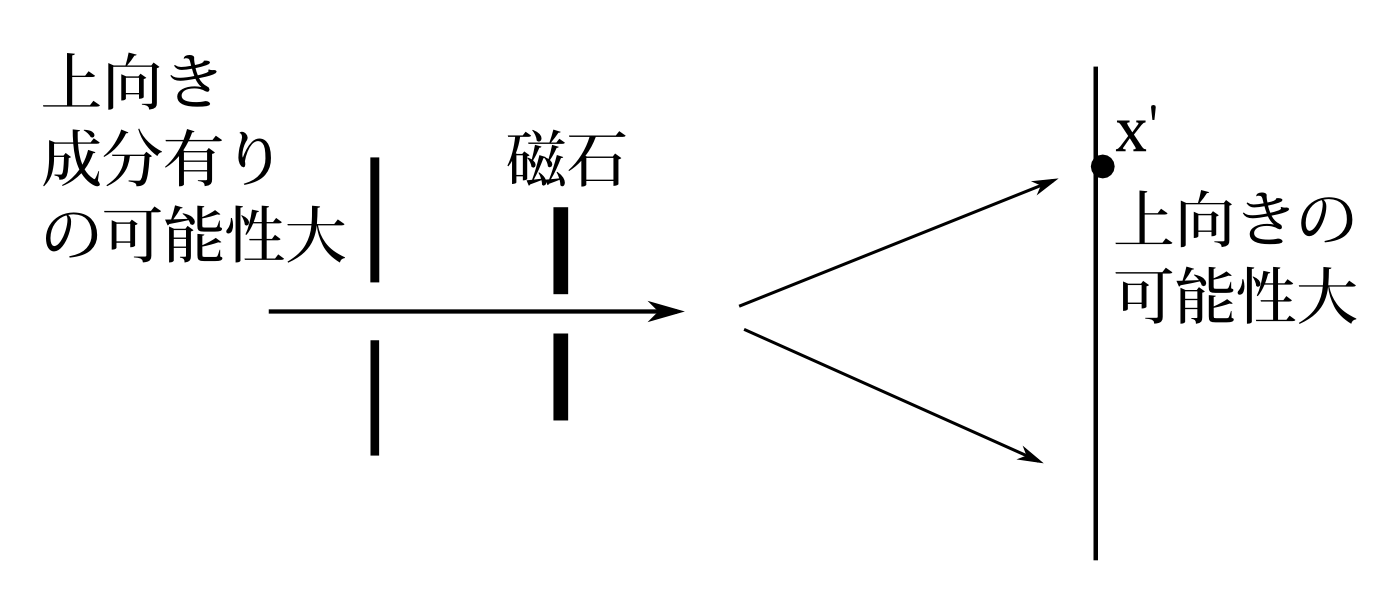
図7.24 回析考慮、初期状態\(\psi(x,s)\)未知
結論
以上の分析結果を以下の表にまとめた。運動量との違いは、測定変数が2つに分かれていて、位置を測定してもスピンは影響を受けないことである。これは2粒子系の場合にも似たような考え方ができ、一方の粒子を測定したことにより、もう一方の粒子の確率振幅は選択され測定される。
| 状況 | スリットでのスピン | スクリーンで検出後のスピン |
| 回析無視、初期状態\(\psi(x,s)\)既知 | \(|\psi(x,s)|^2\) | 上向き |
| 回析無視、初期状態\(\psi(x,s)\)未知 | 上向き成分が0ではない | 上向き |
| 回析考慮、初期状態\(\psi(x,s)\)既知 | \(|\psi(x,s)|^2\) | \(|\psi(x',s)|^2\) |
| 回析考慮、初期状態\(\psi(x,s)\)未知 | 上向き成分が0ではない可能性大 | 上向きの可能性大 |
| 古典軌道論 | 上向き | 上向き |
表の最後の段には古典軌道論(スリット通過時から粒子は古典力学に従うとして扱うこと)の結果も加えた。軌道を量子力学的に扱った測定結果というのは、回析を考慮して、初期状態が未知の場合の下から2段目のものである。スリットでのスピンは古典軌道を通ると考えた場合は上向きと結論され、粒子検出までを量子力学の時間発展方程式で扱った場合は、せいぜい上向きスピンの確率振幅が0でない可能性が大きいとしか言えない。正しいのはもちろん量子力学的に考えた場合であるが、量子論では角運動量の定義が明確でないのでスリットでの角運動量についてああだこうだ言ってもしょうがないと思う。それより何が起きるか、どこで粒子が検出されるかが大事なことだと思う。
今、ここを通過する粒子のスピンを測ってくれといわれても測ることはできない
としか言いようがない。
考察
スリット通過時での、この古典軌道論と量子論での結論の違いについてもう少し突っ込んで考えよう。そのためにこの粒子と相互作用している外部の粒子を含めた確率振幅と言うものを考えよう(注 このことは運動量のときも少し言及したが、スピンの場合、測定変数が位置とスピンに分かれていて話が進めやすいのである。)。外部というのは今の場合で言えば、磁石を構成している粒子であったり、スリットを構成している粒子であったり、スクリーンを構成している粒子であったりする。確率振幅は粒子検出の直前は \[ \psi(x,s,x_外,s_外) \] であったとする。ここで、\(x_外,s_外\)は外部粒子の位置とスピンをまとめて書いた変数である。そして粒子が\(x'\)で検出されたことにより、 \[ \psi(x',s,x_外,s_外) \] という確率振幅に収縮することになる。これを、外部粒子の確率振幅と考えると、検出前には\(x\ne x'\)の場合の確率振幅もあったのに、その中からこの確率振幅が選択されたということを意味する。回析が無視できる状況なら\(s=下\)のときは、この確率振幅は0になるので \[ \psi(x',上,x_外,s_外) \] という確率振幅が選択されたと考えていいだろう。事実としてはただこれだけの話であるが、このスピンが上向きが選択されたということから何か言えないか考えてみよう。
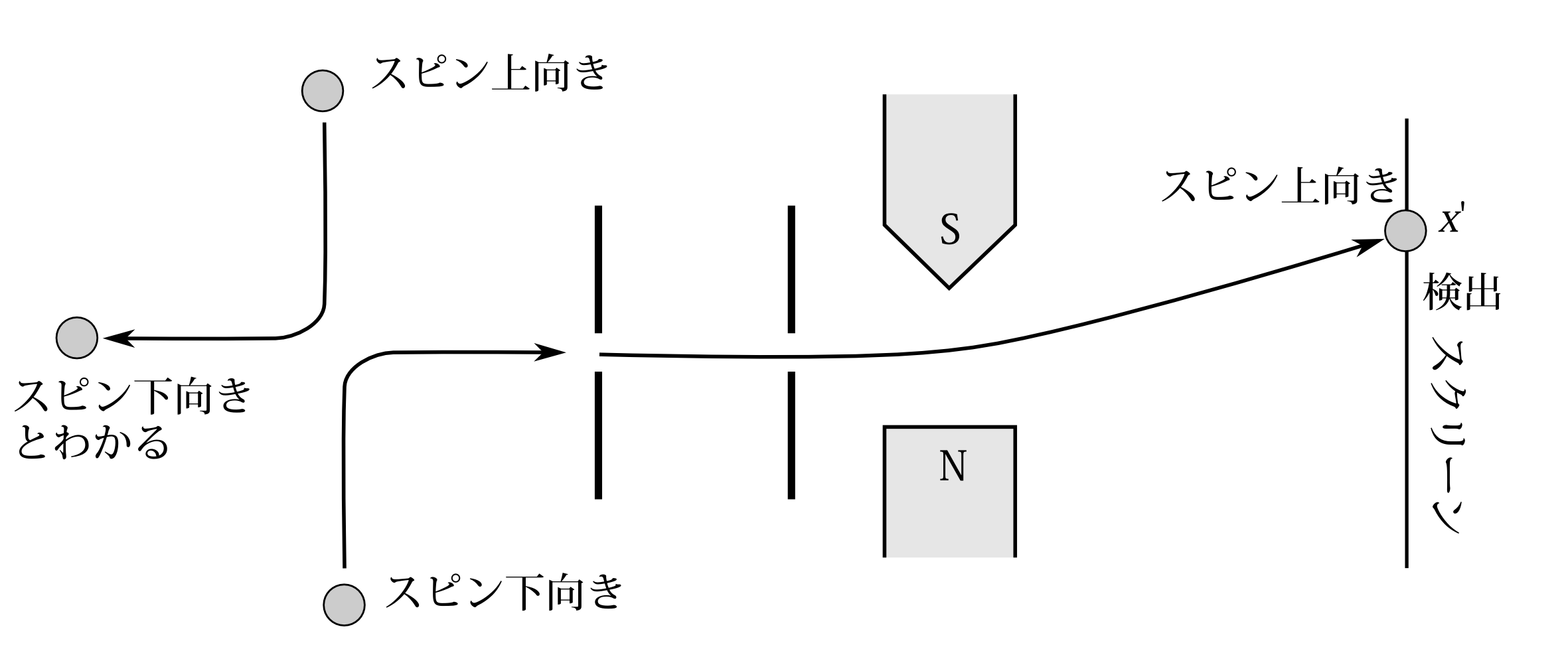
図7.25 2つの粒子のスピンの和が0である粒子を衝突させる。一方の粒子はスリットを通って磁場で曲げられてスクリーンで検出される。\(x'\)で検出されれば、もう一方の粒子のスピンは衝突後に下向きのはずだと結論できる。
今、図7.25のように、スピンが上向きの粒子と下向きの粒子を衝突させたとしよう。衝突後、一方の粒子を、今の実験のようにスリットを通して磁場で曲げてスクリーンの位置\(x'\)で検出したとする。衝突前は \[ \psi(x_1,s_1,x_2,s_2) \] という確率振幅であったとしよう。\(s_1=\)下、かつ\(s_2=\)上のときのみ0でないと言うことなのだから、合計のスピンが0のときのみ確率振幅は0でない。衝突後にどうなるかは――もちろん断定はできないが――古典力学の類推からすると、スピンの合計が0のときのみ確率振幅が0でないと考えるのもそれなりの合理的な推論である。それが成り立つとして話を進めよう。スリットに向かった粒子は、衝突後はおそらく上成分も下成分も持つようになったであろうが、\(x'\)で検出されたということは――回析を無視すれば――下成分は消えて上成分のみになったということである。数式で書くと 粒子が検出される直前の確率振幅が \[ \psi(x_1,s_1,x_2,s_2) \] だったとすると、これは粒子検出によって \[ \psi(x',s_1,x_2,s_2) \] に収縮し、これは\(s_1=\)上のときのみ0でないのだから \[ \psi(x',上,x_2,s_2) \] に収縮するということである。衝突後もスピン変数の和は0のときのみ確率振幅も0でないというのだから、\(s_2=\)下のときのみ、この確率振幅は0でないと言うことになる。つまり、もう一方の粒子のスピンは下向きだと予測できるのである。 一方古典軌道論の考えによれば、\(x'\)で検出されたということはスリット通過時にスピンは上向き、つまり衝突後に上向きだと考えるわけだから、もう一方の粒子は下向きだと考えることになる。結局、軌道を古典力学で扱おうと量子論で扱おうと、もう一方の粒子のスピンに対する結論は同じなのである。 そう考えれば、古典軌道論の考えで、\(x'\)で検出されたなら、スリット通過時にスピンは上向きだったという推測 もあながちおかしな推測ではない。ただ、今のは衝突前の二つの粒子のスピンの状態(少なくともスピンの合計が0だということ)がわかっているという場合であり、初期状態がわからない粒子がスリットを通過したのとは状況が違うことには注意すべきである。又、古典軌道論では回析の効果を全く考慮に入れることができないことも注意すべきである。
多くの粒子で実験する場合の初期状態の推測
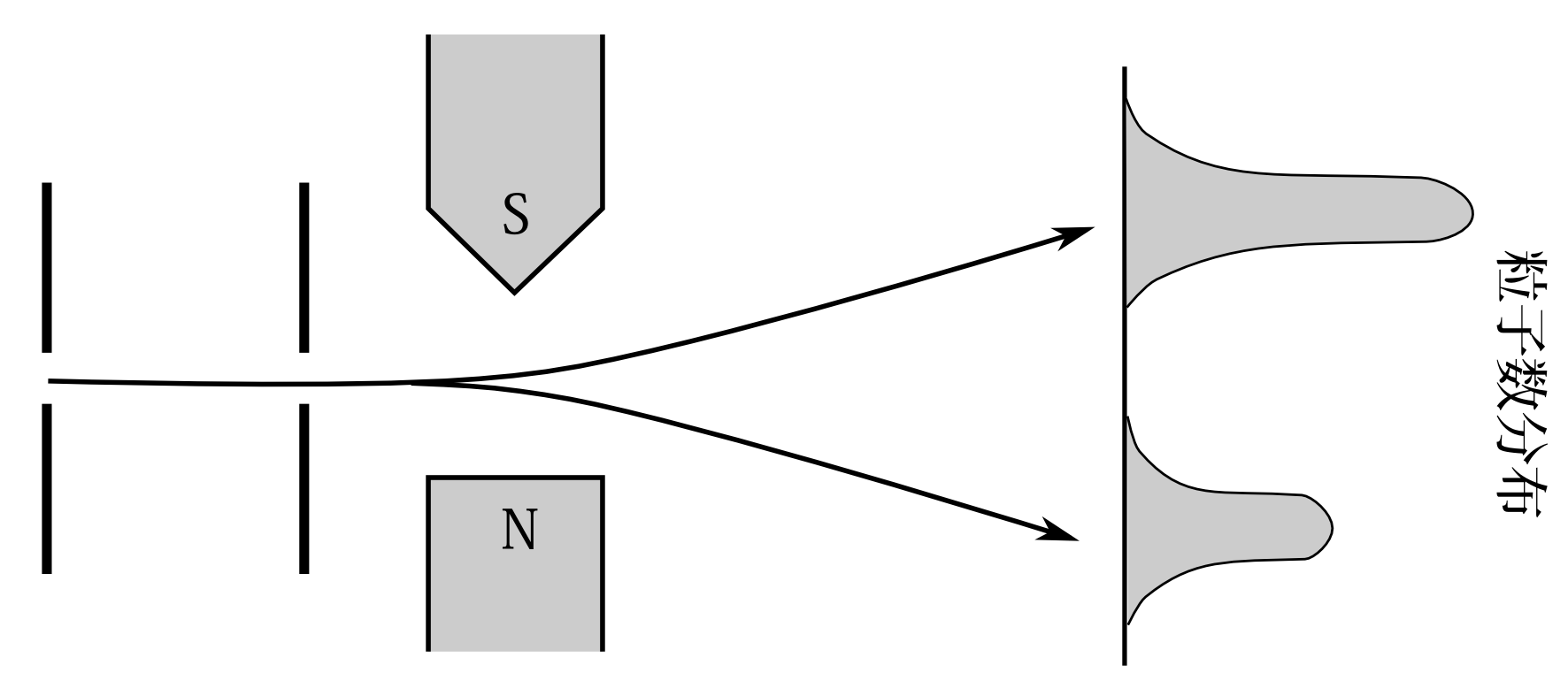
図7.26 全く同じ状況にある膨大な粒子を不均一磁場を通してスクリーンで検出する。上に行く粒子と下に行く粒子の比が2:1だったとしたら、次に来る1個の粒子のスピンに関する確率分布は上向きと下向きの比が2:1と考えていいのではないだろうか。
運動量のときに考えたことをスピンでも考えよう。同じようなことなので簡潔に述べる。 今は粒子が1つだけスクリーンで検出した場合を考えたが、我々の知りうる限り全く同じ状況で膨大な数の粒子がスクリーンに来た場合はどうか。例えば図7.26のように、スクリーンの上と下に来る粒子数比が2:1だったとしたら、次に来る粒子のスリットでの状態は上と下の比がこの2:1の確率分布を持ったものだろうと予想できる。この場合も初期状態が推測できるのである。
スピンの測定状態を作ることができること
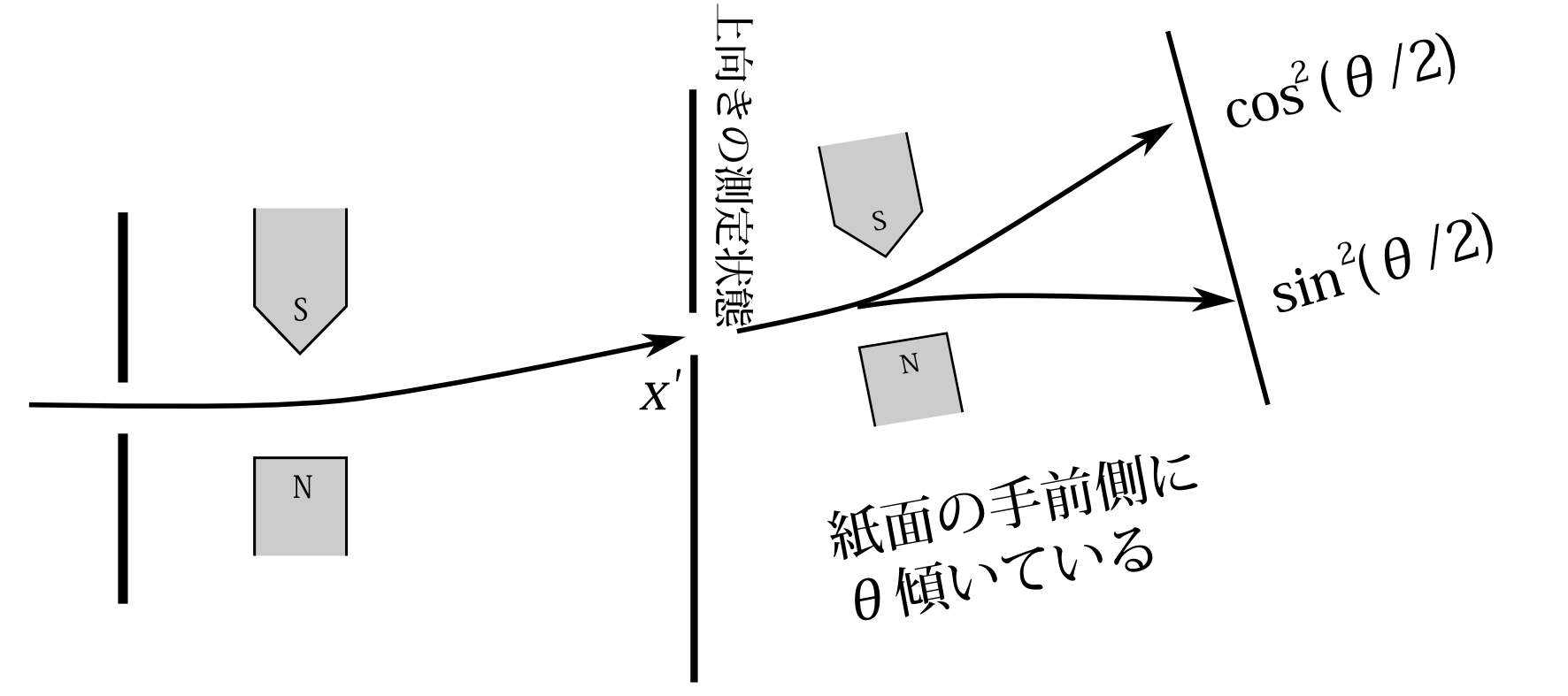
図7.27 \(x'\)を通った粒子はスピン上向きの測定状態になる。
又、図7.27のように、スクリーンの\(x'\)に穴を開けて、粒子を通せば、その状態は――回析が無視できるなら――スピン上向きの測定状態であろう。このようにスピンに関しても測定状態は作ることができる。
古典軌道論と量子軌道論での予測
運動量のときはこの測定状態にある粒子をさらに電場で分離して古典軌道論と量子軌道論の予測が一致することをのべた。スピンの場合も 図7.27のように、上向きに偏った粒子を、例えば紙面の側に\(\theta\)傾けた不均一磁場の中を通 して分離するということが考えられる。波束の運動が量子力学に従うと考えれば 上に行く粒子の割合は\(\cos^2(\theta/2)\)になるだろう(3.1節参照)。古典力学に従うと考えると、上下2つにくっきりと分離することはなく、連続的に分離すると考えられる。ここらへんは運動量の場合と異なり、古典軌道論と量子軌道論で予測が異なる。これはスピンが離散的な値しか取れないことによる特性だろう。
さて、ここでも量子力学は上下に分離する粒子の割合を正確に予測できるということに注意すべきである。\(x'\)を通った粒子のスピンに関する状態はわかっていても位置や運動量に関してはほとんど何もわかっていないにも関わらずにである。 このように膨大な数の粒子に対しては量子力学は正確な予測ができるのである。
7.8節 まとめ
この章で述べたことを大雑把にまとめておこう。 6.1節で述べたように測定とは原則位置を測ることである。 量子力学における測定も、最終的には粒子の位置を測ることに帰着するはずである。そういうわけで、物理量ごとに分離してその位置を測ることによって、その物理量の値を導出するという方法しかない――もちろん、今まで述べてきたようにこの方法では測定になっているとはいい難いのだが――のだと思う。第9章で述べることだが、ハイゼンベルグの顕微鏡などでも電子の位置、運動量を、電子と衝突した光子の位置を測る――ハイゼンベルクはそう扱っていないが――ことによって導出している。 水素原子での電子のエネルギー準位を測る際も、放出される光子を波長ごと(運動量ごと)に分離して光子の位置を測ることによって、光子のエネルギーを導き出し、エネルギー保存則から電子のエネルギーを導き出しているわけである。実際の実験では膨大な量の光子を観測して電子のエネルギーを推定しているので7.5節で述べた膨大な粒子数での実験パターンである。
この章ではこの分離して位置を測るという測定法について――運動量とスピンについて分析したが、スピンの場合は位置とスピン変数という二つの測定変数によって記述されるので、運動量の場合とは多少結論は違ったものになる――分析したわけである。通常の本では、この分離の過程で粒子は古典力学に従って運動しているとして物理量を導出している。しかしこの方法では
【1】 回析の効果を無視している
【2】 位置を検出するまではいろいろな値を持っていたが、位置の検出によってそれらの値は消えたということを無視している
ので正しくない。【1】については粒子は量子力学の時間発展方程式に従うのだから、古典力学の時間発展方程式に従うとした時点で正しくないのである。それがそれなりの有意義な結果を生むのは、波束の運動は、力場の変化が波束に比して小さければ、古典力学の運動方程式に従うからである。そういうわけで、古典力学の運動方程式に従うとするのは明らかに誤りではあるが、測定においてはどこかで古典論の世界に入らなければならないのであって、全くでたらめというわけでないことにも注意すべきである。【2】については、物理量の定義の問題だと言える。スリットでの確率分布自体がその物理量と考えるのか、そうではなく、粒子検出によって波束は収縮し、過去の物理量もくつがえったのだという考えるかである。しかしながら、いずれの考えに立っても、その考えから導出される我々の知覚可能な予想は同じであることが多いと、私は思うので、単に定義の問題なのかもしれない。ここらへんはもっと考えてみる必要があると思っている。知覚可能というのは最終的には――においや音も我々は知覚できるが、物理としては――どこで粒子が検出されるかということだと思う。