第3章 スピン1/2での変換行列と確率振幅
この章は第1章と第2章の応用であり、スピン1/2の系に適用して確率分布から確率振幅と変換行列を求める。
3.1節 スピン状態の特徴
確率分布団から変換行列と確率振幅を求めることを、スピン1/2の系でやってみよう。スピンの場合で変換行列を求めるというのはあまりいい例ではない。今まで考えてきた位置と運動量の変換とはかなり異なる面があるからである。しかし他にいい例もないのでスピン1/2の系でやってみようというわけである。
さて、スピン1/2の粒子というのは以下のような特徴がある。
【特徴1】 任意の状態はどこかの向きの測定状態であり、測定値\(\hbar/2\)
である。
【特徴2】 任意の状態で、任意の向きのスピンを測定すると測定値は
\(\hbar/2\)か\(-\hbar/2\)となる。
【特徴3】 ある向きのスピン\(\hbar/2\)の測定状態にあるとき、別の向きの
スピンを測ってスピンが\(\hbar/2\)である確率は\(\cos^2(\theta/2)\)であ
る。ここで\(\theta\)は2つの向きのなす角で範囲は\(0\le\theta\le\pi\)と制
限する。
【特徴4】 3つの向きでの確率分布――つまり測定値が\(\hbar/2\)か\(-\hbar/2\)
を取る確率――で他のすべての向きの確率分布(すなわち
状態)が決まる。
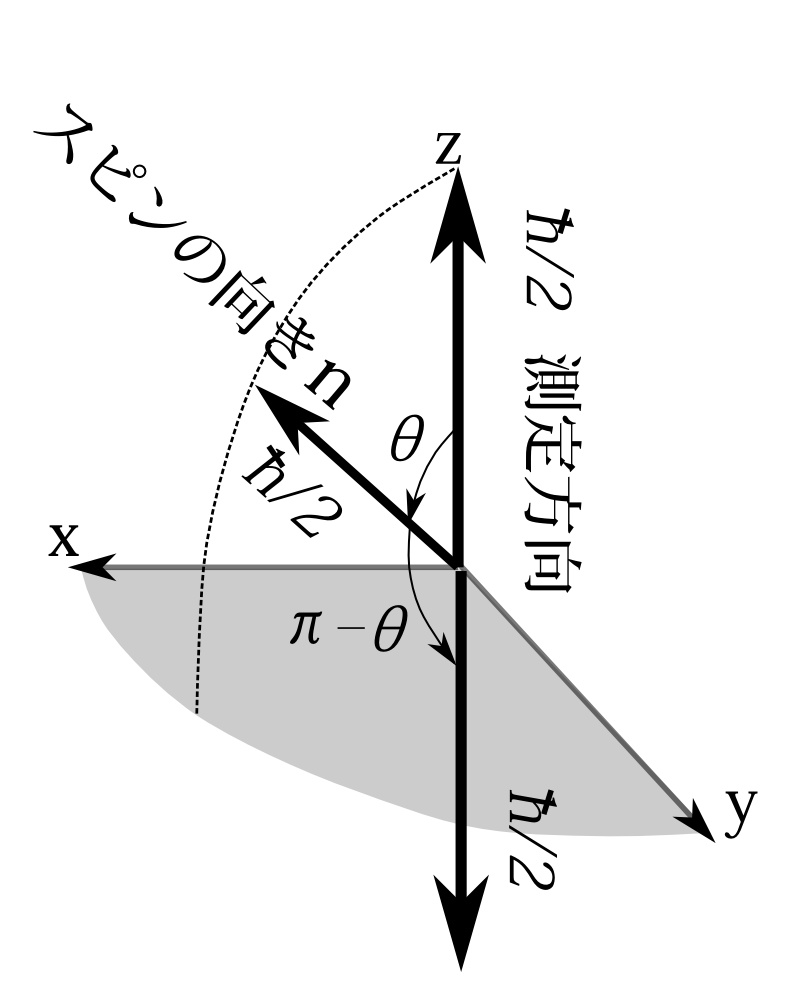
図3.1
これらのことを簡潔に説明する。 【特徴1】は、スピンの任意の状態というのは、図3.1のように必ずどこかの向き――図3.1では\(n\)の向き――を向いていて大きさが\(\hbar/2\)だということである。ただ、あくまで向いていると言うのはわかりやすいイメージである。正確にはその向きでスピン\(\hbar/2\)である確率が1で、\(-\hbar/2\)である確率が0である状態のことである。 【特徴2】は、それを別の方向――図3.1では\(z\)方向――のスピンを測ると、結果は、その向きで大きさが\(\hbar/2\)か逆の向きで大きさが\(\hbar/2\) になるということである。 【特徴3】は、スピンの向きと測定の向きとの角度が\(\theta\)なら、その測定の向きである確率が\(\cos^2(\theta/2)\)だということである。その結果として、逆向きの確率は\(\cos^2[(\pi-\theta)/2]=\sin^2(\theta/2)\)となる(図3.1)。 【特徴4】は、状態はスピンの方向で定まるのだが、図3.2での\(n\)の方向での\(z\)軸と\(x\)軸の確率分布と、\(z,x\)平面で反転した方向\(n'\)での、 \(z\)軸と\(x\)軸の確率分布は同じ確率分布となってしまう。\(z\)軸と\(x\)軸の確率分布だけではどちらの状態かは定まらないのである。それで\(y\)軸での確率分布もわかればどちらの状態かが定まるというわけである。尚、\(y\)軸の確率分布の正確な値まで知る必要はなく、\(y\)軸の正方向と負の方向のどちらの確率が大きいかだけで、方向は定まる。
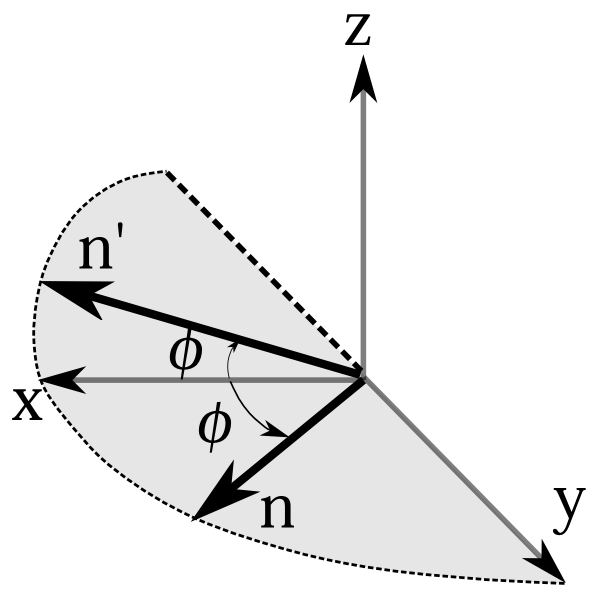
図3.2
3.2節 \(z\)方向の表示から\(x\)方向の表示への変換行列を求める
この節では、2.2節で述べた方法を使って、確率分布から確率振幅と変換行列を求める。 まず記号の説明からしよう。 方向\(n\)に向いている状態での\(z\)軸方向と\(x\)軸方向の確率分布をそれぞれ\(P(z;n+),P(x;n+)\)と書こう。\(n\)と書かずに\(n+\)としたのは――ここではあまり問題ないのだが――後で\(n\)は\(n+\)と\(n-\)をとる変数として使うので、それと区別するためにそうした。 又、方向\(n\)に向いている状態での\(z\)軸方向と\(x\)方向の確率振幅をそれぞれ\(k(z;n+),k(x;n+)\)と書こう (注 通常なら確率振幅は\(\varphi\)や\(\phi\)を使うのだが、極座標の経度で\(\phi\)を使いたいので\(\phi,\varphi\)を使わなかった。\(k\)を使ったのは、任意のスピン状態は必ず測定状態であり、この論文では測定状態の確率振幅は\(k\)を使っているからである。)。 \(z\)は測定変数で、\(\hbar/2\)と\(-\hbar/2\)を取るが、それをそれぞれ\(z+\)、\(z-\)と書こう。 \(x\)も同様。\(z\)方向表示から\(x\)方向表示への変換行列は\(U_{xz}\)と書こう。 方向\(n\)は図3.3のように極座標では\(\theta,\phi\)とする。\(0\le\theta\le\pi\)とする。この制限をしないと【特徴3】の\(\cos^2(\theta/2)\)が成り立たなくなるからである。
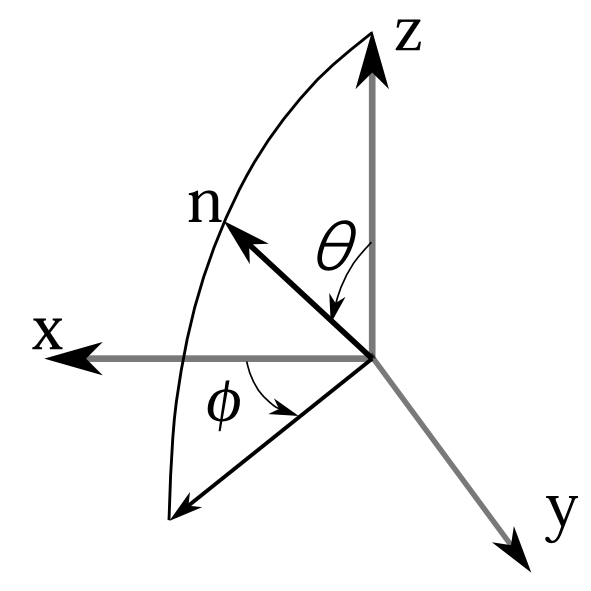
図3.3 極座標。定義域は\(0\le \theta \le \pi\)、\(\phi\)は制限なし。
今からすることというのは \begin{equation} P(z;n+)=|k(z;n+)|^2 \label{1c1} \end{equation} \begin{equation} P(x;n+)=|k(x;n+)|^2 \label{1c2} \end{equation} \begin{equation} k(x;n+)=\sum_z U_{xz}k(z;n+) \label{1c3} \end{equation} を、すべての方向\(n\)で満たす\(U_{xz},k(z;n+),k(x;n+)\)を求めることである。まず、この方程式の前提となる確率分布を求めておこう。【特徴3】より、\(z\)方向の確率分布\(P(z;n+)\)は \begin{equation} \left(\begin{array}{c} P(z+;n+)\\ P(z-;n+) \end{array}\right) = \left(\begin{array}{c} \cos^2(\theta/2)\\ \sin^2(\theta/2) \end{array}\right) \label{1c4} \end{equation} である。次に\(x\)方向の確率分布\(P(x;n+)\)を求めよう。\(n\)方向と\(x\)軸とのなす角を\(\theta_{x}\)と書くと \[ \left(\begin{array}{c} P(x+;n+)\\ P(x-;n+) \end{array}\right) = \left(\begin{array}{c} \cos^2(\theta_{x}/2)\\ \sin^2(\theta_{x}/2) \end{array}\right) = \left(\begin{array}{c} (1+\cos\theta_x)/2\\ (1-\cos\theta_x)/2\\ \end{array}\right) \] である。 ここで半角の公式 \[ \cos^2 (x/2)=(1+\cos x)/2\qquad \sin^2 (x/2)=(1-\cos x)/2 \] を使った。 \(\cos\theta_x\)は\(n\)方向の単位ベクトルの\(x\)成分なので \[\cos\theta_x=\sin\theta\cos\phi\] である。だから\(x\)方向の確率分布は \begin{equation} \left(\begin{array}{c} P(x+;n+)\\ P(x-;n+) \end{array}\right) = \left(\begin{array}{c} (1+\sin\theta\cos\phi)/2\\ (1-\sin\theta\cos\phi)/2\\ \end{array}\right) \label{1c5} \end{equation} である。 この与えられた確率分布で式(\ref{1c1})、(\ref{1c2})、(\ref{1c3})を満たす\(U_{xz}\)と\(k(z;n+)\)と\(k(x;n+)\)を求めたいわけである。
まず、命題1.3より、変換行列の絶対値の2乗は\(z\)方向の測定状態での\(x\)方向で取る確率である。つまり \[ |U_{xz}|^2= \left( \begin{array}{cc} P(x+,z+)&P(x+,z-)\\ P(x-,z+)&P(x-,z-) \end{array} \right) \] ということである。\(z\)軸と\(x\)軸のなす角は\(\pi/2\)なので、【特徴3】より、 \begin{eqnarray} |U_{xz}|^2&=& \left(\begin{array}{cc} \cos^2(\pi/4)&\cos^2(\pi/4)\\ \cos^2(\pi/4)&\cos^2(\pi/4) \end{array}\right) \notag \\ &=&\frac{1}{2} \left( \begin{array}{cc} 1&1\\ 1&1 \end{array} \right)\notag \end{eqnarray} である。 2.2節で述べたように、変換行列は位相の変換すれば特定の行と特定の列をすべて正にできるので、 1行目(これは\(x+\)成分に対応)と1列目(これは\(z+\)成分に対応)を正となるようなものとして、 \begin{equation} U_{xz}= \frac{1}{\sqrt{2}} \left(\begin{array}{cc} 1&1\\ 1&e^{i\delta} \end{array}\right) \label{1c6} \end{equation} とおいてみよう。ここで\(\delta\)は未知数である。
\(n\)方向状態の確率振幅の\(z\)方向表示\(k(z;n+)\)については、 その絶対値の2乗が確率分布 (\ref{1c4})と等しくなるために \begin{equation} \left(\begin{array}{c} k(z+;n+)\\ k(z-;n+) \end{array}\right) = \left(\begin{array}{l} \cos(\theta/2)\\ \sin(\theta/2) e^{i\lambda} \end{array}\right) \label{1c7} \end{equation} とおいてみよう。ここで\(\lambda\)は未知数である。1行目(z+成分)は正となるものを選んだ。これは、2.2節でも述べたが、振幅すべての成分に絶対値1の数を掛けても式(\ref{1c1})、(\ref{1c2})、(\ref{1c3})を満たすということは変わらないので、常に可能である。後は(\ref{1c6})と(\ref{1c7})を(\ref{1c3})の右辺に入れて、\(k(x;n+)\)を未知数\(\delta,\lambda\)で表し、それを(\ref{1c2})の右辺に代入して、すべての方向\(n\)で(\ref{1c2})が成り立つように未知数\(\delta,\lambda\)を求めることである。
ところで、今の場合、変換行列\(U_{xz}\)はユニタリー行列でなければならないということから \( \delta=\pi \)と求まってしまう。つまり \[ U_{xz}= \frac{1}{\sqrt{2}} \left(\begin{array}{cc} 1&1\\ 1&-1 \end{array}\right) \] と定まってしまう。ただユニタリー行列でなければならないということを使わなくても、上記の手順を踏めば\(\delta\)は求まる。 ではそれを淡々と実行して、未知数を求めよう。 (\ref{1c6})と(\ref{1c7})を(\ref{1c3})の右辺に入れて、 \[ k(x;n+) = \frac{1}{\sqrt{2}} \left( \begin{array}{cc} 1&1\\ 1&e^{i\delta} \end{array} \right) \left( \begin{array}{l} \cos(\theta/2)\\ \sin(\theta/2) e^{i\lambda} \end{array} \right) = \frac{1}{\sqrt{2}} \left( \begin{array}{l} \cos(\theta/2)+\sin(\theta/2) e^{i\lambda}\\ \cos(\theta/2)+\sin(\theta/2) e^{i(\lambda+\delta)} \end{array} \right) \] そして \begin{eqnarray*} |k(x;n+)|^2 &=& \frac{1}{2} \left(\begin{array}{l} \cos^2(\theta/2)+\sin^2(\theta/2)+\cos(\theta/2)\sin(\theta/2)\left(e^{i\lambda}+e^{-i\lambda}\right)\\ \cos^2(\theta/2)+\sin^2(\theta/2)+\cos(\theta/2)\sin(\theta/2)\left(e^{i(\lambda+\delta)}+e^{-i(\lambda+\delta)}\right) \end{array}\right) \\ &=& \frac{1}{2} \left(\begin{array}{l} 1+\sin\theta\cos\lambda\\ 1+\sin\theta\cos(\lambda+\delta) \end{array}\right) \end{eqnarray*} となる。(\ref{1c2})の左辺は(\ref{1c5})で与えられているので、方程式(\ref{1c2})は \[ \frac{1}{2} \left(\begin{array}{l} 1+\sin\theta\cos\phi\\ 1-\sin\theta\cos\phi \end{array}\right) = \frac{1}{2} \left(\begin{array}{l} 1+\sin\theta\cos\lambda\\ 1+\sin\theta\cos(\lambda+\delta) \end{array}\right) \] となる。この解は、一行目から \( \lambda=\pm \phi \) と求まる。2行目から、 \( \delta=\pi \) と求まる。こうして \begin{equation} U_{xz}= \frac{1}{\sqrt{2}} \left(\begin{array}{cc} 1&1\\ 1&-1 \end{array}\right) \label{1e1} \end{equation} \begin{equation} k(z;n+)= \left(\begin{array}{l} \cos(\theta/2)\\ \sin(\theta/2)e^{\pm i\phi} \end{array}\right) \label{1ea} \end{equation} と求まるわけである。解が2つあるのは第2章で述べたように、互いに複素共役の2つのグループがあるからである (注 実のところは、解として\(\pm\phi\)があるのは、幾何学的に見ても(\ref{1c5})を見てもわかるように、経度\(\phi\)が\(-\phi\)でも\(x\)方向では同じ確率分布であることも理由の1つである。ただこのことを考えるとややこしくなるので考えないことにする。 。)
3.3節 \(z\)方向から任意の方向への表示の変換行列
今の結果を使って\(z\)方向表示から、任意の方向\(n\)表示への変換行列を求めよう。 命題1.2より、\(n\)方向表示から\(z\)方向表示への変換行列\(U_{zn}\)は、\(n\)方向の測定状態の\(z\)方向表示、つまり \[ U_{zn}=k(z;n) \] である。ここで\(n\)は測定変数で\(n+\)と\(n-\)をとるとする。極座標で\(n+\)の向きは\((\theta_+,\phi_+)\)、\(n_-\)の向きは\((\theta_-,\phi_-)\)だとしよう。\(n+\)と\(n-\)は互いに反対の向きなので \begin{equation} \theta_-=\pi-\theta_+ \qquad \phi_-=\phi_++\pi \label{hantai} \end{equation} の関係にある(図3.4)。すると(\ref{1ea})より
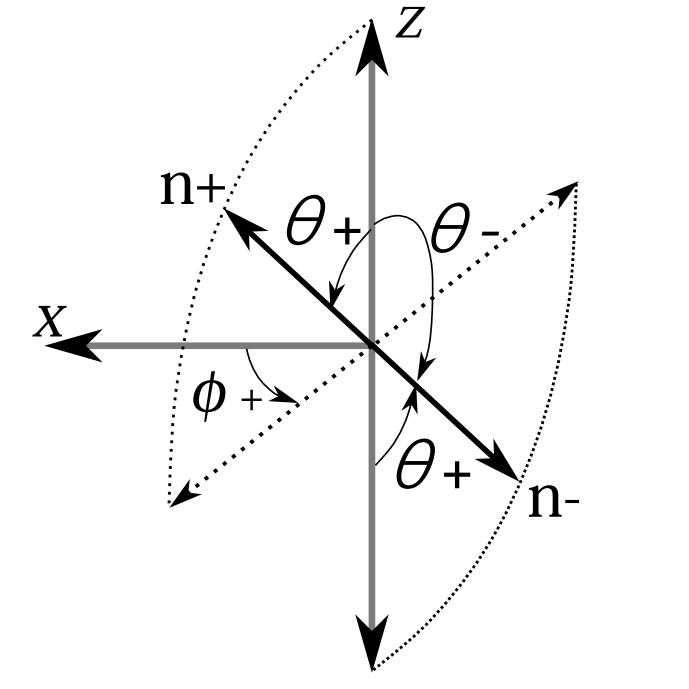
図3.4
\begin{eqnarray*} U_{zn}&=&\Big(k(z;n+),k(z;n-)\Big)\\ &=&\left(\begin{array}{ll} \cos(\theta_+/2)&\cos(\theta_-/2)\\ \sin(\theta_+/2)e^{\pm i\phi_+}&\sin(\theta_-/2) e^{\pm i\phi_-} \end{array}\right) \end{eqnarray*} である。 変換行列\(U_{nz}\)はこの転置共役で \[ U_{nz}= \left(\begin{array}{cc} \cos(\theta_+/2)&\sin(\theta_+/2)e^{\mp i\phi_+}\\ \cos(\theta_-/2)&\sin(\theta_-/2) e^{\mp i\phi_-} \end{array}\right) \] である。これを\(n+\)方向の角度\(\theta_+.\phi_+\)のみで表すと、それを\(\theta,\phi\)と書くが、(\ref{hantai})の関係より \begin{equation} U_{zn} = \left(\begin{array}{cc} \cos(\theta/2)&\sin(\theta/2)\\ \sin(\theta/2)e^{\pm i\phi}&-\cos(\theta/2)e^{\pm i\phi} \end{array}\right) \qquad U_{nz}= \left(\begin{array}{cc} \cos(\theta/2)&\sin(\theta/2) e^{\mp i\phi}\\ \sin(\theta/2)&-\cos(\theta/2) e^{\mp i\phi} \end{array}\right) \label{1121} \end{equation} である。これはユニタリー行列になってくれている。ただ\(\pm\phi\)の\(+\phi\)の方を使ったら、もう一方でも\(+\phi\)を使わなければならず、\(-\phi\)を使ったらもう一方でも\(-\phi\)を使わなければユニタリー行列にはならない。
正しい確率分布を示すこと
さて、任意の状態の\(n\)方向表示を考えよう。任意の状態はどこかの向きの測定状態なので、その向きを極座標で\(\theta',\phi'\)として、\(n'\)方向と呼ぼう。 すると、その状態の\(z\)方向表示\(k(z;n'+)\)は \[ k(z;n'+)= \left(\begin{array}{l} \cos\theta'\\ \sin\theta' e^{\pm i\phi'} \end{array}\right) \] である。この状態の\(n\)方向表示 \(k(n;n'+)\)は \begin{eqnarray} k(n;n'+)&=&\sum_z U_{nz}k(z;n'+)\notag\\ &=& \left(\begin{array}{cc} \cos(\theta_+/2)&\sin(\theta_+/2)e^{\mp i\phi_+}\\ \cos(\theta_-/2)&\sin(\theta_-/2) e^{\mp i\phi_-} \end{array}\right) \left(\begin{array}{l} \cos\theta'\notag\\ \sin\theta' e^{\pm i\phi'} \end{array}\right) \\ &=& \left(\begin{array}{c} \cos(\theta_+/2)\cos(\theta'/2)+\sin(\theta_+/2)\sin(\theta'/2)e^{\mp i(\phi_+-\phi')}\\ \cos(\theta_-/2)\cos(\theta'/2)+\sin(\theta_-/2)\sin(\theta'/2)e^{\mp i(\phi_--\phi')} \end{array}\right) \label{nn'} \end{eqnarray} である(注 このときも\(\pm \phi\)や\(\mp \phi\)で、\(U_{nz}\)で上の記号を使ったら(今の場合\(-\phi\))、\(k(z;n'+)\)でも上の記号(今の場合\(+\phi\))を使わなければならないし、\(U_{nz}\)で下の記号を使ったら\(k(z;n'+)\)でも下の記号を使わなければならない。上の計算では実際にそうしているが、そうしないと \(\phi_{\pm}-\phi'\)の部分が\(\phi_{\pm}+\phi'\)になってしまい 異なる確率分布になってしまう。)。
さて、この 変換によってできる確率振幅\(k(n;n'+)\)が意味を成すためには、最初にのべた【特徴3】の \begin{equation} |k(n+;n'+)|^2=\cos^2(\alpha_+/2)\qquad |k(n-;n'+)|^2=\cos^2(\alpha_-/2) \label{kyoukaku} \end{equation} を満たしていなければならない。ここで\(\alpha_+\)は\(n+\)方向と\(n'\)方向とのなす角。\(\alpha_-\)は\(n-\)方向と\(n'\)方向のなす角。 これが成り立つかどうかは決して自明ではない。というのは\(n\)方向状態の\(z\)方向表示の確率振幅は単に式(\ref{1c1})、(\ref{1c2})、(\ref{1c3})を満たすということだけから求めたのであり、\(z\)方向表示と\(x\)方向表示でだけ【特徴3】を満たすように決めただけだからである。
さて、それを調べてみよう。そのためには\(n=n+\)のときの \begin{equation} \left|k(n+;n'+)\right|^2=\cos^2(\alpha_+/2) \label{1d2} \end{equation} だけ調べれば十分であり、 \(n=n-\)場合まで調べる必要はない。というのは (\ref{nn'})の最後の式を見てわかるように、1行目と2行目の違いは\(\theta_+,\phi_+\)が\(\theta_-,\phi_-\)に置き換わっただけであり、\(\theta_+,\phi_+\)は、今からの証明において任意の角度として扱うからである。 では、まずこの(\ref{1d2})の右辺から計算しよう。\(\theta_+,\phi_+,\alpha_+\)はもう添え字をつけて区別する必要もないので、それぞれ
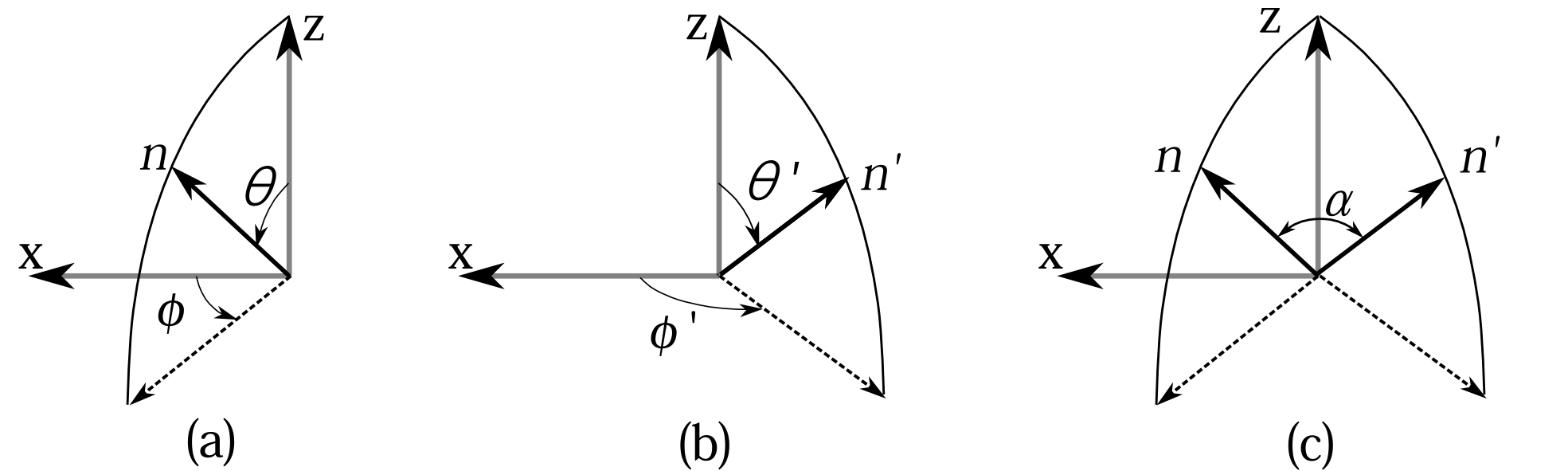
図3.5
\(\theta,\phi,\alpha\)と書くことにする。方向の関係は図3.5のようになる。 \(\cos\alpha\)は\(n\)方向と\(n'\)方向の単位ベクトルの内積に等しいので \[ \cos\alpha=\sin\theta\cos\phi\cdot \sin\theta'\cos\phi'+\sin\theta\sin\phi\cdot \sin\theta'\sin\phi'+\cos\theta\cdot \cos\theta' \] である。半角の公式を使うと \begin{eqnarray} \cos^2\left(\frac{\alpha}{2}\right)&=&\frac{1}{2}(1+\cos\alpha)\notag\\ &=&\frac{1}{2}(1+\sin\theta\cos\phi\cdot \sin\theta'\cos\phi'+\sin\theta\sin\phi\cdot \sin\theta'\sin\phi'+\cos\theta\cdot \cos\theta') \label{1d1} \end{eqnarray} となる。(\ref{1d2})の左辺は少し面倒である。(\ref{nn'})より \begin{eqnarray} &&\left|k(n+;n'+)\right|^2\notag\\ &=&\left|\cos(\theta/2)\cos(\theta'/2)+\sin(\theta/2)\sin(\theta'/2)e^{\mp i(\phi-\phi')}\right|^2\notag\\ &=& \cos^2(\theta/2)\cos^2(\theta'/2)+\sin^2(\theta/2)\sin^2(\theta'/2)+ \cos(\theta/2)\cos(\theta'/2)\sin(\theta/2)\sin(\theta'/2)\left(e^{i(\phi-\phi')}+e^{-i(\phi-\phi')}\right)\notag\\ &=& \frac{1+\cos\theta}{2}\cdot\frac{1+\cos\theta'}{2}+\frac{1-\cos\theta}{2}\cdot\frac{1-\cos\theta'}{2}+\frac{\sin\theta}{2}\cdot\frac{\sin\theta'}{2}\cdot 2\cos(\phi-\phi')\notag\\ &=& \frac{\Big[1+\cos\theta\cos\theta'+\sin\theta\sin\theta'\left(\cos\phi\cos\phi'+\sin\phi\sin\phi'\right)\Big]}{2}\notag\\ &=& \frac{1}{2}(1+\sin\theta\cos\phi\cdot \sin\theta'\cos\phi'+\sin\theta\sin\phi\cdot \sin\theta'\sin\phi'+\cos\theta\cdot \cos\theta') \label{1d3} \end{eqnarray} となり、これは(\ref{1d1})に等しい。よって(\ref{1d2})は成り立つというわけである。なんとも不思議にうまくいっているものである。不思議だと感じるのは私がその本質を理解していないからであろう。うまく行っているということは、【特徴3】で述べた\(\cos^2(\theta/2)\)が正しいことの間接的根拠になっていると思う。\(\cos^2(\theta/2)\)でなかったらうまく行かないのではないか。
\(z\)方向から\(x\)方向、\(y\)方向への変換行列
さて、\(z\)方向表示から\(x\)方向表示への変換行列\(U_{xz}\)は、 すでに求めたように(\ref{1e1}) である。\(z\)方向表示から任意の方向の\(n\)方向表示への変換行列は(\ref{1121})であり、再掲すると \[ U_{nz}= \left(\begin{array}{cc} \cos(\theta/2)&\sin(\theta/2) e^{\mp i\phi}\\ \sin(\theta/2)&-\cos(\theta/2) e^{\mp i\phi} \end{array}\right) \] である。\(x\)方向は\(\theta=\pi/2,\phi=0\)なので代入すると \[ U_{xz}=\frac{1}{\sqrt{2}} \left(\begin{array}{cc} 1&1\\ 1&-1 \end{array}\right) \] となり、(\ref{1e1})と等しくなってくれている。これはたまたまで、詳しいことは省くが、(\ref{1c7})の確率振幅で1行目の\(z+\)成分を\(\cos(\theta/2)\)と正に設定したからである。 \(y\)方向表示への変換は\(\theta=\pi/2,\;\phi=\pi/2\)として、\(\mp \phi\)で\(-\phi\)の方を使うと(こちらの方が時間発展方程式の関係から正しい位相だからである(第3.4節参照)。)、 \begin{eqnarray} U_{yz}&=& \left(\begin{array}{cc} \cos(\pi/4)&\sin(\pi/4) e^{-i\pi/2}\\ \sin(\pi/4)&-\cos(\pi/4)e^{-i\pi/2} \end{array}\right)\notag\\ &=& \frac{1}{\sqrt{2}} \left(\begin{array}{cc} 1&-i\\ 1&i \end{array}\right) \label{yz} \end{eqnarray} となる。
3.4節 時間発展方程式との関係
(\ref{1ea})の確率振幅\(k(z;n+)\)は \[ k(z;n+)= \left(\begin{array}{l} \cos(\theta/2)\\ \sin(\theta/2)e^{\pm i\phi} \end{array}\right) \] と\(\phi\)と\(-\phi\)の2つあった。これは2.4節で述べたように時間発展方程式と関係がある。どちらが \[ i\hbar\frac{d\varphi_\varepsilon}{dt}=\varepsilon\varphi_\varepsilon \] に合っているのかを調べよう。ここで\(\varphi_\varepsilon\)はエネルギー表示での確率振幅。

図3.6
今スピン1/2の荷電粒子が一様な磁場\(B>0\)の中にあるとし、\(z\)方向を磁場の向きに取るとしよう(図3.6)。 この場合、エネルギー測定値\(\varepsilon\)は、CGSガウス単位系で \[ \varepsilon= \left\{ \begin{array}{l} -\frac{q}{mc}B\left(\frac{\hbar}{2}\right)\\ -\frac{q}{mc}B\left(-\frac{\hbar}{2}\right) \end{array} \right. \] の2つだと考えられる。ここで\(q\)は電荷、\(m\)は質量、\(c\)は光速。 そしてエネルギー測定値が\(\varepsilon=-\frac{q}{mc}B\left(\frac{\hbar}{2}\right)\)のエネルギー測定状態というのは、磁場の方向である\(z+\)方向の状態であり、エネルギー測定値が\(\varepsilon=-\frac{q}{mc}B\left(-\frac{\hbar}{2}\right)\)のエネルギー測定状態というのは、\(z-\)方向の状態であると考えられる。エネルギーの原点を\(-\frac{q}{mc}B\left(\frac{\hbar}{2}\right)\)とすると、\(z+\)状態ではエネルギーは0、\(z-\)状態ではエネルギーは\(\frac{q}{mc}B\hbar\) となる。エネルギー表示でもあり\(z\)方向表示でもある時間発展方程式は、時刻\(t\)での\(z+\)方向の確率振幅を\(k_+(t)\)、\(z-\)方向の確率振幅を\(k_-(t)\)とし、\(\frac{qB}{mc}=a\)とおいて、 \begin{eqnarray*} i\hbar\frac{dk_+(t)}{dt}&=&0\cdot k_{+}(t) \\ i\hbar\frac{dk_{-}(t)}{dt}&=&a\hbar\cdot k_{-}(t) \end{eqnarray*} となる。時刻\(t=0\)で、図3.6のように極座標で\(\theta_0,\phi_0\)を向いているとすると、時刻\(t\)での解は \begin{eqnarray*} k_{+}(t)&=&k_{+}(0)=\cos(\theta_0/2) \\ k_{-}(t)&=&k_{-}(0)e^{-at}=\sin(\theta_0/2)e^{i\left(\pm \phi_0-at \right)} \end{eqnarray*} となる。 今電荷が正\(q>0\)とすると\(a=\frac{qB}{mc}>0\)となる。この場合\(\pm\phi\)のうち、\(+\phi\)を採用するなら、経度という意味での\(\phi\)は減る方向に動く。\(-\phi\)なら増える方向に動く。それで現実に合う方が決まる。尚、古典電磁気学から類推すると、この状況では経度が減る方向へ回転する――その理由は難しくないのだが省略する――ので、おそらくこの時間発展方程式に合う確率振幅は\(+\phi\)の方であろう。 つまり \[ k(z;n+)= \left(\begin{array}{l} \cos(\theta/2)\\ \sin(\theta/2)e^{i\phi} \end{array}\right) \] の方が現実に合う。
3.5節 まとめ
この章での計算結果をまとめて書いておこう。 間の角が\(\theta\)であるときの確率が\(\cos^2(\theta/2)\)であることを使って、確率分布団を求め、\(z\)方向表示から\(x\)方向表示への変換行列が \[ U_{xz}= \frac{1}{\sqrt{2}} \left(\begin{array}{cc} 1&1\\ 1&-1 \end{array}\right) \] となること、任意の\(n+\)状態の\(z\)方向表示が、\(n\)方向は極座標で\(\theta,\phi,0\le \theta\le \pi\)として、 \[ k(z;n+)= \left(\begin{array}{l} \cos(\theta/2)\\ \sin(\theta/2)e^{\pm i\phi} \end{array}\right) \] であることを求めた。尚、これは\(\theta=0,\pi\)で連続でない。時間発展方程式と合うのは\(\pm \phi\)の\(+\phi\)の方であった。そしてこの方向から\(z\)方向表示への変換行列とその逆は、\(+\phi\)の方で、 \[ U_{zn}= \left(\begin{array}{cc} \cos(\theta/2)&\sin(\theta/2)\\ \sin(\theta/2)e^{i\phi}&-\cos(\theta/2)e^{i\phi} \end{array}\right) \qquad\qquad U_{nz}= \left(\begin{array}{cc} \cos(\theta/2)&\sin(\theta/2)e^{-i\phi}\\ \sin(\theta/2)&-\cos(\theta/2)e^{-i\phi} \end{array}\right) \] であった。\(x\)方向表示と\(z\)方向表示の変換行列は \[ U_{zx}= \frac{1}{\sqrt{2}} \left(\begin{array}{cc} 1&1\\ 1&-1 \end{array}\right) \qquad\qquad U_{xz}= \frac{1}{\sqrt{2}} \left(\begin{array}{cc} 1&1\\ 1&-1 \end{array}\right) \] であり、\(y\)方向表示と\(z\)方向表示の変換行列は \[ U_{zy}= \frac{1}{\sqrt{2}} \left(\begin{array}{cc} 1&1\\ i&-i \end{array}\right) \qquad\qquad U_{yz}= \frac{1}{\sqrt{2}} \left(\begin{array}{cc} 1&-i\\ 1&i \end{array}\right) \] であった。
3.6節 補足――変換行列と確率振幅の他の表現
2.1節で述べたように、確率振幅と変換行列には任意性がある。それで補足として この章で求めた変換行列と確率振幅を別のもので表してみよう。\((\theta,\phi)\)方向の\(z\)方向表示 \[ k(z;\theta,\phi)= \left(\begin{array}{l} \cos(\theta/2)\\ \sin(\theta/2)e^{i\phi} \end{array}\right) \] というのは対称性がよくない。それで新しい表示として \[ \left(\begin{array}{l} \cos(\theta/2)e^{-i\phi/2}\\ \sin(\theta/2)e^{ i\phi/2} \end{array}\right) \] となるようにしたい。
1回目の変換
そこで、\((\theta,\phi)\)状態の確率振幅はいろんな方向の表示があるわけだが、その――\(z\)方向表示も含め――すべての表示に\(e^{-i\phi/2}\)を掛けよう。すると\((\theta,\phi)\)状態の\(z\)方向表示は \begin{equation} k'(z;\theta,\phi)= \left(\begin{array}{l} \cos(\theta/2)e^{-i\phi/2}\\ \sin(\theta/2)e^{ i\phi/2} \end{array}\right) \label{ko-a} \end{equation} になってくれる。この新しい確率振幅は\(k'\)とダッシュを付けて元々のものと区別することにする。この操作はすべての表示に対して絶対値が1である定数\(e^{-i\phi/2}\)を掛けるパターンであり、変換行列\(U\)はそのままでよい。 状態が変われば\(\phi\)も変化するので、状態ごとに掛ける数が変わることに注意。例えば\(\phi=45\)°の状態に対しては、すべての表示の確率振幅に\(e^{-i(\pi/4)/2}\)を掛けるし、 \(\phi=90\)°の状態に対しては、すべての表示の確率振幅に\(e^{-i(\pi/2)/2}\)

図3.7 1回目の変換。経度が\(\phi\)である状態には\(e^{-i\phi/2}\)をすべての表示に掛ける。
を掛けることになる(図3.7)。ところで、今、元の確率振幅に\(e^{-i\phi/2}\)を掛けて新しい確率振幅を作り出したわけだが、この\(\phi\)の定義域を明確にしておかないと、いったい何を掛けたかわからなくなるし、その新しい確率振幅自体もどういう値なのかわからなくなる。というのは\(\phi\)と\(\phi+2\pi\)は同じ方向を指すが、\(e^{-i(\phi+2\pi)/2}\ne e^{-i\phi/2}\)というように値が異なるからである。\(\phi\)の定義域は範囲が\(2\pi\)ならなんでもいいが、\(0\le \phi<2\pi\)や\(-\pi\le \phi<\pi\)ぐらいを使うのがいいのではないかと思う。このように (\ref{ko-a})の表し方だと、少しややこしいところもあるが、1行目と2行目で角度\(\phi\)に関しての対称性はよくなる。
対称性について
この対称性に関して少し補足しよう。まず\((\theta,\phi)\)方向を改めて\(\theta_{z+},\phi_{z+}\)と書き直そう。これは\(z\)の正方向と\(x\)軸を基軸とした極座標だと言える。又、この\((\theta,\phi)\)方向を、\(z\)の負方向と\(x\)軸を基軸とした極座標で表したものを\(\theta_{z-},\phi_{z-}\)と書くとしよう(図3.8)。このとき\(\phi_{z-}=-\phi_{z+}\)の関係にある。というのは\(z\)の負方向の軸と\(x\)を基軸とすると回転の正の向きが逆になるからである(図3.8)。又、\(\theta_{z-}=\pi-\theta_{z+}\)である(図3.8)。だから(\ref{ko-a})は \begin{equation} k'(z;\theta,\phi)= \left(\begin{array}{l} \cos(\theta_{z+}/2)e^{-i\phi_{z+}/2}\\ \cos(\theta_{z-}/2)e^{ -i\phi_{z-}/2} \end{array}\right) \label{sin-b} \end{equation} となり、1行目の\(z+\)状態の役割と2行目の\(z-\)状態の役割が全く同じになる。

図3.8
2回目の変換
少し脱線してしまったが、話を戻そう。今\(n+\)方向というのは\((\theta_+,\phi_+)\)方向を向いているとしよう。そして\(n-\)方向は\(n+\)の逆向きで\((\theta_-,\phi_-)\)方向だとしよう。 \(n+\)状態と\(n-\)状態の、\(n\)表示は元々は \begin{equation} k(n;n+)= \left(\begin{array}{c} 1\\ 0 \end{array}\right)\qquad\qquad k(n;n-)= \left(\begin{array}{c} 0\\ 1 \end{array}\right) \label{ta} \end{equation} であったが、この新たな確率振幅だと(ダッシュ付きの方)\(n+\)状態のすべての表示に\(e^{-i\phi_+/2}\)を掛け、\(n-\)状態のすべての表示に\(e^{-i\phi_-/2}\)を掛けたのだから \[ k'(n;n+)= \left(\begin{array}{c} e^{-i\phi_+/2}\\ 0 \end{array}\right) \qquad\qquad k'(n;n-)= \left(\begin{array}{c} 0\\ e^{-i\phi_-/2} \end{array}\right) \] となる。これでも物理としては全く問題ないのだが、測定状態のその物理量での表示なので、できたら(\ref{ta})のように標準的な形になって欲しい。 そこで2.1節で行った変換行列も含めた変換(第2章、式(3)、式(4)参照)をほどこそう。任意の状態\(\lambda\)での\(n\)表示の確率振幅\(k'(n;\lambda)\)から、新たな確率振幅\(k''(n;\lambda)\)を \begin{equation} k''(n;\lambda)= \left(\begin{array}{l} e^{i\phi_+/2}\times k'(n+;\lambda)\\ e^{i\phi_-/2}\times k'(n-;\lambda) \end{array}\right) \label{pm304} \end{equation} というように作る。 こうすれば\(\lambda=n+\)、\(\lambda=n-\)のときそれぞれ \[ k''(n;n+)= \left(\begin{array}{c} 1\\ 0 \end{array}\right) \qquad\qquad k''(n;n-)= \left(\begin{array}{c} 0\\ 1 \end{array}\right) \] になってくれる。この変換は表示ごとにあらゆる状態に対して同じ変換をす
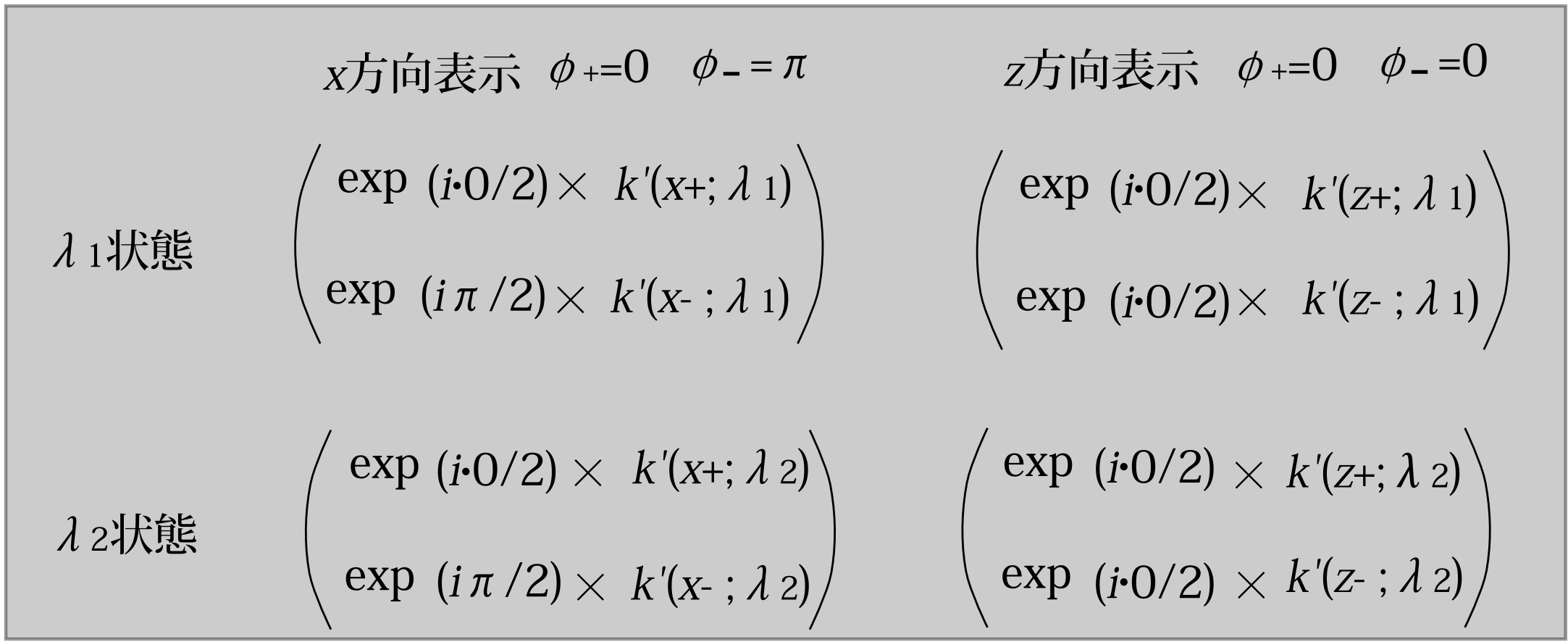
図3.9 2回目の変換。表示方向の経度が\(\phi\)なら、すべての状態に対して\(e^{i\phi/2}\)を掛ける。
るのであり、例えば\(x\)方向表示なら\(\phi_+=0,\phi_-=\pi\)なので(経度\(\phi\)の定義域が\(0\le \phi<2\pi\)のとき)、すべての状態\(\lambda\)に対して \[ k''(x;\lambda)= \left(\begin{array}{l} e^{i\cdot 0/2}\times k'(x+;\lambda)\\ e^{i\pi/2}\times k'(x-;\lambda) \end{array}\right) \] と変換されるし(図3.9)、\(z\)方向表示なら\(\phi_+=0,\phi_-=0\)なので \[ k''(z;\lambda)= \left(\begin{array}{l} e^{i\cdot 0/2}\times k'(z+;\lambda)\\ e^{i\cdot 0/2}\times k'(z-;\lambda) \end{array}\right) \] となる(図3.9)。つまり \[ k''(z;\lambda)=k'(z;\lambda) \] と\(z\)方向表示は(\ref{ko-a})のままであってくれる。 あとはこれに合わせて変換行列を変えればよい。今興味があるのは任意の\(n\)方向から\(z\)方向への変換行列で
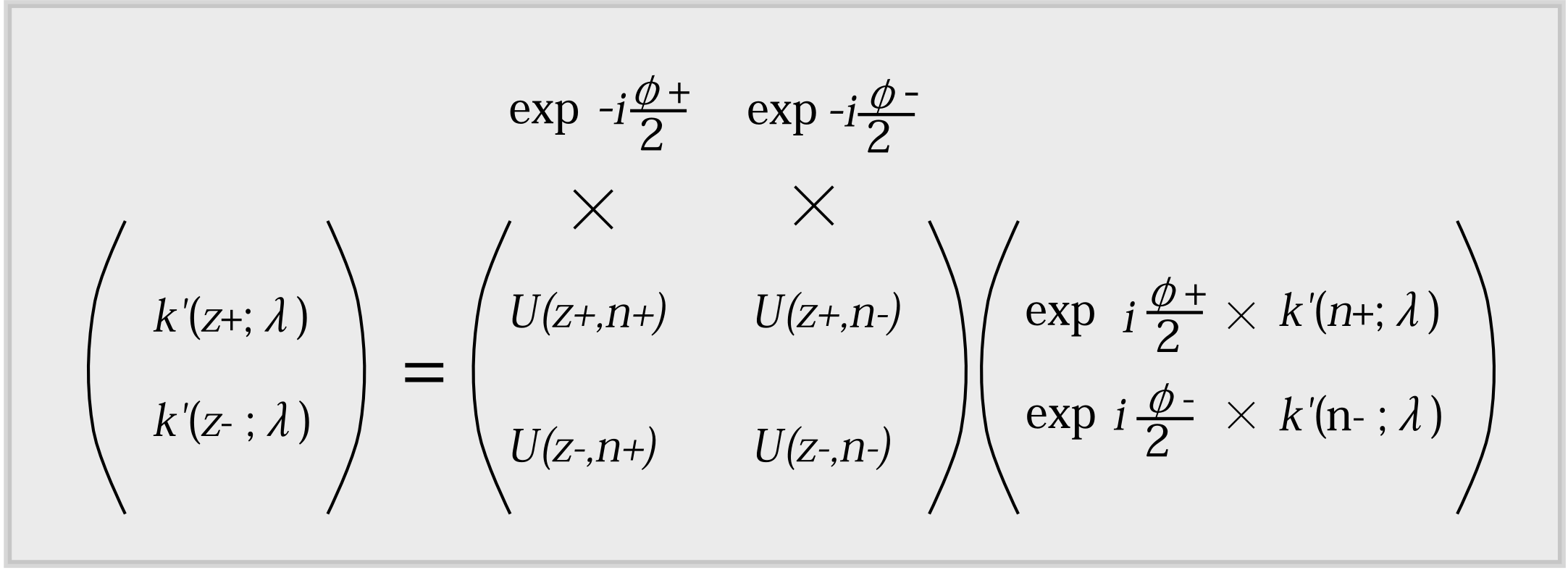
図3.10 変換行列の変換。\(z\)方向表示は変化ないので行には何も掛けない。
ある。それは図3.10のように \(U_{zn}\)の1列目(これは\(n+\)に相当)に\(e^{-i\phi_+/2}\)を、2列目(これは\(n-\)に相当)に\(e^{-i\phi_-/2}\)を掛ければよい。となると新たな変換行列\(U'_{zn}\)は \begin{equation} U'_{zn}= \left(\begin{array}{cc} \cos(\theta_+/2)e^{-i\phi_+/2}&\cos(\theta_-/2)e^{-i\phi_-/2}\\ \sin(\theta_+/2)e^{i\phi_+/2}&\sin(\theta_-/2)e^{i\phi_-/2} \end{array}\right) \label{sin} \end{equation} となる。これは(\ref{ko-a})と比較すればわかるように、単に\(n+\)状態の\(z\)方向表示である\(k'(z;n+)\)と、\(n-\)状態の\(z\)方向表示である\(k'(z;n-)\)を並べたもの、つまり \begin{equation} U'_{zn}=\Big(k'(z;n+),k'(z;n-)\Big) \label{sin-a} \end{equation} になっている。というよりもなっているべきだったのである。しかしそうあるべきだからと言って、いきなりこの2つを並べて変換行列を作っただけではその正しさがわからない。というのはこの変換行列によって作り出される新たな確率振幅が、第3.3節で述べたように、正しい確率分布を与えること(確率が\(\cos^2(\text{狭角}/2)\)となること。式(\ref{kyoukaku})参照)を示さなければならないからである。しかし今のように2.1節で述べた確率振幅と変換行列の変換の手続きをふめば、この新しい確率振幅に対応する確率分布は変わらないので、改めて確認する必要はないのである。
再び対称性について
尚、再び脱線するが\(U'_{zn}\)は(\ref{sin-a})であり、(\ref{sin-b})のように\(z\)の正の軸、負の軸から見た角度を使って表すと \[ U'_{zn}= \left(\begin{array}{cc} \cos\big[\theta(n+,z+)/2\big]e^{-i\phi(n+,z+)/2}&\cos\big[\theta(n-,z+)/2\big]e^{-i\phi(n-,z+)/2}\\ \cos\big[\theta(n+,z-)/2\big]e^{-i\phi(n+,z-)/2}&\cos\big[\theta(n-,z-)/2\big]e^{-i\phi(n-,z-)/2} \end{array}\right) \] となる。ここで、例えば\(\phi(n+,z-)\)と言うのは\(z-\)軸から見た\(n+\)方向の経度という意味である。他も同様。 だから\(n\)方向表示から基軸となる\(z\)方向への表示の変換成分は \[ U'_{zn}=\cos[\theta(n,z)/2]e^{-i\phi(n,z)/2} \] である。ここで\(n\)は\(n+,n-\)を取る変数。\(z\)も\(z+,z-\)を取る変数。又、基軸である\(z\)方向表示から\(n\)方向への表示の変換成分はこの複素共役である \[ U'_{nz}=\cos[\theta(n,z)/2]e^{i\phi(n,z)/2} \] となる。又、ついでながら書いておくと、\(n\)方向状態の\(z\)方向表示は \[ k(z;n)=\cos[\theta(n,z)/2]e^{-i\phi(n,z)/2} \] である。このように、正方向、負方向の区別もなく対称性があり物理的にすっきりする。 しかしながら、この極座標の\((\theta,\phi)\)というのは、\(z\)方向から見た角度であり、\(n\)方向から見た角度ではない。その点では対称性はない。
具体的な変換行列
さて話を元に戻すが、この(\ref{sin})の\(\theta_-,\phi_-\)を消去し、\(\theta_+,\phi_+\)で表しておこう。\(\theta\)に関しては\(\theta_-=\pi-\theta_+\)でいいのだが、\(\phi\)に関しては、\(\phi\)の定義域と\(\phi_+\)の値によって \(\phi_-=\phi_++\pi\)の場合と\(\phi_-=\phi_+-\pi\)の場合がある。それをまとめて\(\phi_-=\phi_+\pm\pi\)と書いておこう。これらを使って(\ref{sin})を\(+\)方向の角度で表し、さらに\(+\)の添字も省くと \[ U'_{zn}= \left(\begin{array}{cc} \cos(\theta/2)e^{-i\phi/2}&\mp i\sin(\theta/2)e^{-i\phi/2}\\ \sin(\theta/2)e^{i\phi/2}&\pm i\cos(\theta/2)e^{i\phi/2} \end{array}\right) \qquad U'_{nz}= \left(\begin{array}{cc} \cos(\theta/2)e^{i\phi/2}&\sin(\theta/2)e^{-i\phi/2}\\ \pm i\sin(\theta/2)e^{i\phi/2}&\mp i\cos(\theta/2)e^{-i\phi/2} \end{array}\right) \] となる。又\(n\)方向として\(x\)方向をとるなら変換行列は、\(\theta=\pi/2,\phi=0\)を入れ、 \[ U'_{zx}= \frac{1}{\sqrt{2}} \left(\begin{array}{cc} 1&\mp i\\ 1&\pm i \end{array}\right) \qquad\qquad U'_{xz}= \frac{1}{\sqrt{2}} \left(\begin{array}{cc} 1&1\\ \pm i&\mp i \end{array}\right) \] となる。尚、\(\phi\)の定義域として\(0\le \phi<2\pi\)とするなら、\(x\)軸方向は\(\phi_+=0,\phi_-=\pi\)なので、\(\phi_-=\phi_++\pi\)であり、上の符号の方である。\(-\pi\le \phi<\pi\)とするなら、\(\phi_-=\phi_+-\pi\)であり、下の符号の方である。 又\(n\)方向として\(y\)方向をとるなら、変換行列は、\(\theta=\pi/2,\phi=\pi/2\)を入れ、 \[ U'_{zy}= \frac{1}{2} \left(\begin{array}{cc} 1-i&\mp(1+i)\\ 1+i&\pm(-1+i) \end{array}\right) \qquad\qquad U'_{yz}= \frac{1}{2} \left(\begin{array}{cc} 1+i&1-i\\ \mp(1-i)&\pm(-1-i) \end{array}\right) \] となる。
まとめ
話が脱線したりして長くなってしまったが、実際行ったことは単純なことである。それを簡潔にまとめておこう。 状態\(\lambda\)の経度は\(\phi_\lambda\)だとする。その状態\(\lambda\)の\(n\)方向表示確率振幅\(k(n;\lambda)\)をまず \[ k'(n;\lambda)=e^{-i\phi_\lambda/2} k(n;\lambda) \] と変換する。変換行列はそのままである。次に\(n\)方向表示の確率振幅を変換するが、\(n+\)方向の経度を\(\phi_{n+}\)、\(n-\)方向の経度を\(\phi_{n-}\)とし、\(n\)を\(n+\)と\(n-\)をとる変数と考えて、これをまとめて\(\phi_n\)と書くことにする。これを使って\(n\)方向表示を \[ k''(n;\lambda)=e^{i\phi_n/2}k'(n;\lambda) \] と変換する。これに合わせて\(n\)方向表示から\(n'\)方向表示への変換行列\(U_{n'n}\)を変換する。\(n'\)方向の経度は\(\phi_{n'}\)とする。ここでの\(n'\)は\(n'+\)と\(n'-\)をとる変数。これを使って\(U_{n'n}\)を \[ U'_{n'n}=e^{i\phi_{n'}/2}U_{n'n}e^{-i\phi_{n}/2} \] と変換する。 結局、 最初の確率振幅\(k(n;\lambda)\)、変換行列\(U_{n'n}\)からは \[ k''(n;\lambda)=e^{i(\phi_n-\phi_\lambda)/2}k(n;\lambda)\qquad\qquad U'_{n'n}=e^{i\phi_{n'}/2}U_{n'n}e^{-i\phi_{n}/2} \] という変換を行ったということである。その結果\((\theta,\phi)\)方向の\(z\)方向表示が \[ k''(z;\theta,\phi)= \left(\begin{array}{l} \cos(\theta/2)e^{-i\phi/2}\\ \sin(\theta/2)e^{ i\phi/2} \end{array}\right) \] となり、\((\theta,\phi)\)方向表示から\(z\)方向表示への変換行列が \[ U'_{z;\theta,\phi}= \left(\begin{array}{cc} \cos(\theta/2)e^{-i\phi/2}&\mp i\sin(\theta/2)e^{-i\phi/2}\\ \sin(\theta/2)e^{i\phi/2}&\pm i\cos(\theta/2)e^{i\phi/2} \end{array}\right) \] となったわけである。ここでの\(\pm\)や\(\mp\)は、表示の向きの正方向と逆方向の経度の関係が\(\phi_-=\phi_+\pm\pi\)となることによるもの。